In mathematics, a self-avoiding walk (SAW) is a sequence of moves on a lattice

Lattice (group)

In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...

 that does not visit the same point more than once. A self-avoiding polygon (SAP) is a closed self-avoiding walk on a lattice. SAWs were first introduced by the chemist Paul Flory

Paul Flory

Paul John Flory was an American chemist and Nobel laureate who was known for his prodigious volume of work in the field of polymers, or macromolecules...

 in order to model the real-life behavior of chain-like entities such as solvent

Solvent

A solvent is a liquid, solid, or gas that dissolves another solid, liquid, or gaseous solute, resulting in a solution that is soluble in a certain volume of solvent at a specified temperature...

s and polymer

Polymer

A polymer is a large molecule composed of repeating structural units. These subunits are typically connected by covalent chemical bonds...

s, whose physical volume prohibits multiple occupation of the same spatial point. Very little is known rigorously about the self-avoiding walk from a mathematical perspective, although physicists have provided numerous conjectures that are believed to be true and are strongly supported by numerical simulations.

In computational physics

Computational physics

Computational physics is the study and implementation of numerical algorithms to solve problems in physics for which a quantitative theory already exists...

 a self-avoiding walk is a chain-like path in or 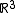with a certain number of nodes, typically a fixed step length and has the imperative property that it doesn't cross itself or another walk. A system of self-avoiding walks satisfies the so called excluded volume

Excluded volume

The concept of excluded volume was introduced by Werner Kuhn in 1934 and applied to polymer molecules shortly thereafter by Paul Flory.- In liquid state theory :...

 condition. In higher dimensions, the self-avoiding walk is believed to behave much like the ordinary random walk

Random walk

A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...

. SAWs and SAPs play a central role in the modelling of the topological

Topology

Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...

 and knot-theoretic

Knot theory

In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...

 behaviour of thread- and loop-like molecules such as protein

Protein

Proteins are biochemical compounds consisting of one or more polypeptides typically folded into a globular or fibrous form, facilitating a biological function. A polypeptide is a single linear polymer chain of amino acids bonded together by peptide bonds between the carboxyl and amino groups of...

s. SAW is a fractal

Fractal

A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...

. For example, in d=2 the fractal dimension

Fractal dimension

In fractal geometry, the fractal dimension, D, is a statistical quantity that gives an indication of how completely a fractal appears to fill space, as one zooms down to finer and finer scales. There are many specific definitions of fractal dimension. The most important theoretical fractal...

 is 4/3, for d=3 it is close to 5/3 while for d≥4 the fractal dimension is 2. The dimension is called the upper critical dimension

Critical dimension

In the renormalization group analysis of phase transitions in physics, a critical dimension is the dimensionality of space at which the character of the phase transition changes. Below the lower critical dimension there is no phase transition. Above the upper critical dimension the critical...

 above which excluded volume is negligible.

The properties of SAWs cannot be calculated analytically, so numerical simulation

Simulation

Simulation is the imitation of some real thing available, state of affairs, or process. The act of simulating something generally entails representing certain key characteristics or behaviours of a selected physical or abstract system....

s are employed. The pivot algorithm is a common method for Markov chain Monte Carlo

Markov chain Monte Carlo

Markov chain Monte Carlo methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the...

 simulations for the uniform measure on n-step self-avoiding walks. The pivot algorithm works by taking a self-avoiding walk and randomly choosing a point on this walk, and then applying a symmetry operation (rotations and reflections) on the walk after the nth step to create a new walk. Calculating the number of self-avoiding walks in any given lattice is a common computational problem. There is currently no known formula for determining the number of self-avoiding walks, although there are rigorous methods for approximating them. Finding the number of such paths is conjectured to be an NP-hard

NP-hard

NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...

 problem. For self-avoiding walks from one diagonal to the other, with only moves in the positive direction, there are exactly 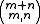paths for an m × n rectangular lattice.

Universality

One of the phenomena associated with self-avoiding walks and 2d statistical physics models in general is the notion of universality, that is, independence of macroscopic observables from microscopic details, such as the choice of the lattice. One important quantity that appears in conjectures for universal laws is the connective constant, defined as follows. Let denote the number of n-step self-avoiding walks. Since every n+m step self avoiding walk can be decomposed into an n-step self-avoiding walk and an m-step self-avoiding walk, it follows that 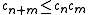. Then by applying Fekete's lemma to the logarithm of the above relation, the limit can be shown to exist. This number is called the connective constant, and clearly depends on the particular lattice chosen for the walk since does. 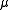The value of is only precisely known for the hexagonal lattice, where it is equal to 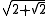. For other lattices, 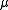has only been approximated numerically, and is believed to not even be an algebraic number. It is conjectured that 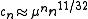as n goes to infinity, where 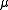depends on the lattice, but the power law correction does not, in other words, this law is believed to be universal.

Limits

Consider the uniform measure on -step self-avoiding walks in the full plane. It is currently unknown whether the limit of the uniform measure as goes to infinity induces a measure on infinite full-plane walks. However, Harry Kesten

Harry Kesten

Harry Kesten is an American mathematician best known for his work in probability, most notably on random walks and percolation theory.- Biography :...

 has shown that such a measure exists for self-avoiding walks in the half-plane. One important question involving self-avoiding walks is the existence and conformal invariance of the scaling limit, that is, the limit as the length of the walk goes to infinity and the mesh of the lattice goes to zero. The scaling limit of the self-avoiding walk is conjectured to be described by Schramm-Loewner Evolution with parameter .

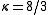External links

• Java applet of a 2D self-avoiding walk