
Fractal dimension on networks
Encyclopedia
Self-similarity of complex networks
Many real networks have two fundamental properties, scale-free property and small-worldWatts and Strogatz model
The Watts and Strogatz model is a random graph generation model that produces graphs with small-world properties, including short average path lengths and high clustering. It was proposed by Duncan J. Watts and Steven Strogatz in their joint 1998 Nature paper...
property. If the degree distribution
Degree distribution
In the study of graphs and networks, the degree of a node in a network is the number of connections it has to other nodes and the degree distribution is the probability distribution of these degrees over the whole network.-Definition:...
of the network follows a power-law, the network is scale-free; if any two arbitrary nodes in a network can be connected in a very small number of steps, the network is said to be small-world.
The small-world properties can be mathematically expressed by the slow increase of the average diameter
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
of the network, with the total number of nodes
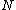 ,
,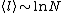
where
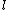 is the shortest distance between two nodes.
is the shortest distance between two nodes.Equivalently, we obtain:
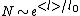
where
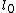 is a characteristic length.
is a characteristic length.For a self-similar structure, a power-law relation is expected rather than the exponential relation above. From this fact, it would seem that the small-world networks are not self-similar under a length-scale transformation.
However, analysis of a variety of real complex networks shows they are self-similar on all length scales, a conclusion derived from measuring a power-law relation between the number of boxes needed to cover the network and the size of the box, so called fractal scaling.
The methods for calculation of the dimension
Generally we calculate the fractal dimension using either the Box Counting Method or the Cluster Growing Method.

The Box Counting Method
Let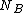 be the number of boxes of linear size
be the number of boxes of linear size 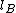 , needed to cover the given network. The fractal dimension
, needed to cover the given network. The fractal dimensionFractal dimension
In fractal geometry, the fractal dimension, D, is a statistical quantity that gives an indication of how completely a fractal appears to fill space, as one zooms down to finer and finer scales. There are many specific definitions of fractal dimension. The most important theoretical fractal...
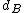 is then given by
is then given by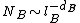
This means that the average number of vertices
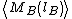 within a box of size
within a box of size 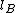
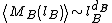
By measuring the distribution of
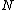 for different box sizes or by measuring the distribution of
for different box sizes or by measuring the distribution of 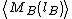 for different box sizes, the fractal dimension
for different box sizes, the fractal dimension 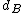 can be obtained by a power law fit of the distribution.
can be obtained by a power law fit of the distribution.The Cluster Growing Method
One seed node is chosen randomly. If the minimum distance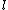 is given, a cluster of nodes separated by at most
is given, a cluster of nodes separated by at most 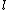 from the seed node can be formed. The procedure is repeated by choosing many seeds until the clusters cover the whole network. Then the dimension
from the seed node can be formed. The procedure is repeated by choosing many seeds until the clusters cover the whole network. Then the dimension 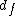 can be calculated by
can be calculated by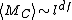
where
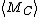 is the average mass of the clusters, defined as the average number of nodes in a cluster.
is the average mass of the clusters, defined as the average number of nodes in a cluster.These methods are difficult to apply to networks since networks are generally not embedded in another space. In order to measure the fractal dimension of networks we add the concept of renormalization.
Box-counting and Renormalization

For each size lB, boxes are chosen randomly (as in the cluster growing method) until the network is covered, A box consists of nodes separated by a distance l < lB. Then each box is replaced by a node(renormalization). The renormalized nodes are connected if there is at least one link between the unrenormalized boxes. This procedure is repeated until the network collapses to one node. Each of these boxes has an effective mass (the number of nodes in it) which can be used as shown above to measure the fractal dimension of the network. In Fig.(3b), renormalization is applied to a WWW network through three steps for lB = 3.
Fig.(5) shows the invariance of the degree distribution P(k) under the renormalization performed as a function of the box size on the World Wide Web. The networks are also invariant under multiple renormalizations applied for a fixed box size lB. This invariance suggests that the networks are self-similar on multiple length scales.
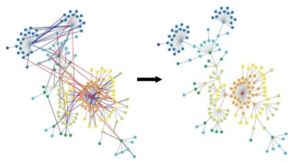
Skeleton and Fractal Scaling
The fractal properties of the network can be seen in its underlying tree structure. In this view, the network consists of the skeleton and the shortcuts. The skeleton is a special type of spanning tree, formed by the edges having the highest betweenness centralitiesCentrality
Within graph theory and network analysis, there are various measures of the centrality of a vertex within a graph that determine the relative importance of a vertex within the graph...
, and the remaining edges in the network are shortcuts.
If the original network is scale-free, then its skeleton also follows a power-law degree distribution, where the degree can be different from the degree of the original network. For the fractal networks following fractal scaling, each skeleton shows fractal scaling similar to that of the original network. The number of boxes to cover the skeleton is almost the same as the number needed to cover the network.
Real-world fractal networks
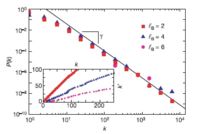
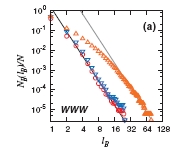
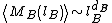 ,
,we can investigate whether a network is fractal and what is the fractal dimension of the network. For example, the WWW, metabolic network, protein interaction network(PIN) of H. sapiens, and PIN of S. cerevisiaeare considered as fractal networks. Furthermore, the fractal dimensions measured are
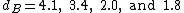 for the networks respectively. On the other hand, the Internet, actor network, and artificial models (for instance, the BA model) do not show the fractal properties.
for the networks respectively. On the other hand, the Internet, actor network, and artificial models (for instance, the BA model) do not show the fractal properties.Other definitions for network dimensions
The best definition of dimension for a complex networkComplex network
In the context of network theory, a complex network is a graph with non-trivial topological features—features that do not occur in simple networks such as lattices or random graphs but often occur in real graphs...
or graph
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
depends on the application. For example, metric dimension
Metric dimension (graph theory)
In graph theory, the metric dimension of a graph G is the minimum number of vertices in a subset S of G such that all other vertices are uniquely determined by their distances to the vertices in S...
is defined in terms of the resolving set for a graph. Definitions based on the scaling property of the "mass" as defined above with distance,
or based on the complex network zeta function
Complex network zeta function
Different definitions have been given for the dimension of a complex network or graph. For example, metric dimension is defined in terms of the resolving set for a graph. Dimension has also been defined based on the box covering method applied to graphs. Here we describe the definition based on...
have also been studied.
For networks embedded in real space, one can define a dimension that characterize the number of nodes that can be reached with an average Euclidean distance.

