
Feigenbaum function
Encyclopedia
In the study of dynamical systems the term Feigenbaum function has been used to describe two different functions introduced by the physicist Mitchell Feigenbaum
:
of period doubling. The equation is used to specify a function g and a parameter λ by the relation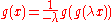
with the boundary conditions
For a particular form of solution with a quadratic dependence of the solution
near x=0, the inverse 1/λ=2.5029... is one of the Feigenbaum constants.
of the logistic map
at the end of the period-doubling cascade. The attractor is a Cantor set
set, and just as the middle-third Cantor set, it can be covered by a finite set of segments, all bigger than a minimal size dn. For a fixed dn the set of segments forms a cover Δn of the attractor. The ratio of segments from two consecutive covers, Δn and Δn+1 can be arranged to approximate a function σ, the Feigenbaum scaling function.
Mitchell Feigenbaum
Mitchell Jay Feigenbaum is a mathematical physicist whose pioneering studies in chaos theory led to the discovery of the Feigenbaum constants.- Biography :...
:
- the solution to the Feigenbaum-Cvitanović functional equation; and
- the scaling function that described the covers of the attractorAttractorAn attractor is a set towards which a dynamical system evolves over time. That is, points that get close enough to the attractor remain close even if slightly disturbed...
of the logistic mapLogistic mapThe logistic map is a polynomial mapping of degree 2, often cited as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations...
Functional equation
The functional equation arises in the study of one-dimensional maps that, as a function of a parameter, go through a period-doubling cascade. The functional equation is the mathematical expression of the universalityUniversality (dynamical systems)
In statistical mechanics, universality is the observation that there are properties for a large class of systems that are independent of the dynamical details of the system. Systems display universality in a scaling limit, when a large number of interacting parts come together...
of period doubling. The equation is used to specify a function g and a parameter λ by the relation
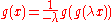
with the boundary conditions
- g(0) = 1,
- g′(0) = 0, and
- g′′(0) < 0
For a particular form of solution with a quadratic dependence of the solution
near x=0, the inverse 1/λ=2.5029... is one of the Feigenbaum constants.
Scaling function
The Feigenbaum scaling function provides a complete description of the attractorAttractor
An attractor is a set towards which a dynamical system evolves over time. That is, points that get close enough to the attractor remain close even if slightly disturbed...
of the logistic map
Logistic map
The logistic map is a polynomial mapping of degree 2, often cited as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations...
at the end of the period-doubling cascade. The attractor is a Cantor set
Cantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
set, and just as the middle-third Cantor set, it can be covered by a finite set of segments, all bigger than a minimal size dn. For a fixed dn the set of segments forms a cover Δn of the attractor. The ratio of segments from two consecutive covers, Δn and Δn+1 can be arranged to approximate a function σ, the Feigenbaum scaling function.

