Bifurcation theory - AbsoluteAstronomy.com

Bifurcation theory is the mathematical

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

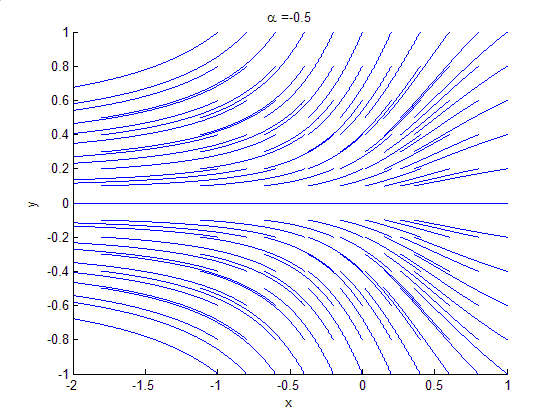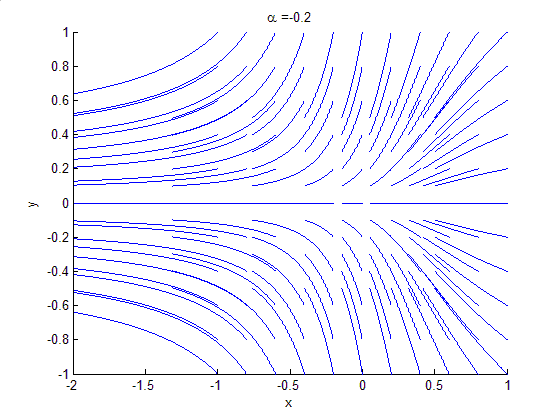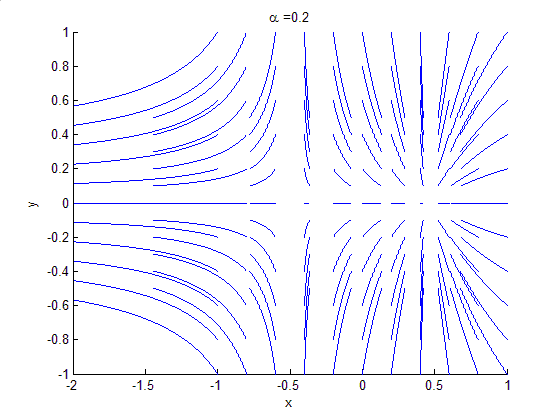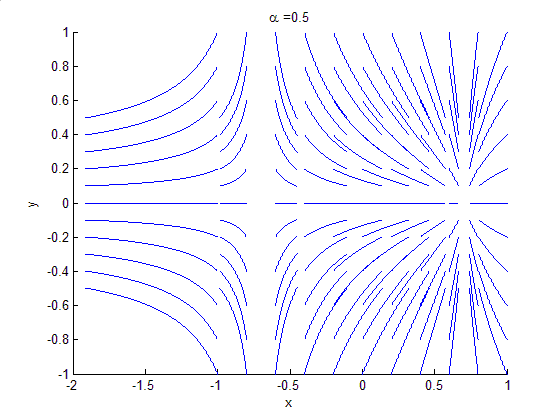
study of changes in the qualitative or topological structure of a given family, such as the integral curve

Integral curve

In mathematics, an integral curve is a parametric curve that represents a specific solution to an ordinary differential equation or system of equations...

s of a family of vector field

Vector field

In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...

s, and the solutions of a family of differential equation

Differential equation

A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...

s. Most commonly applied to the mathematical

Mathematics

study of dynamical systems, a bifurcation occurs when a small smooth change made to the parameter values (the bifurcation parameters) of a system causes a sudden 'qualitative' or topological change in its behaviour. Bifurcations occur in both continuous systems (described by ODE

Ordinary differential equation

In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....

s, DDE

Delay differential equation

In mathematics, delay differential equations are a type of differential equation in which the derivative of the unknown function at a certain time is given in terms of the values of the function at previous times....

s or PDEs

Partial differential equation

In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...

), and discrete systems (described by maps).

Bifurcation types

It is useful to divide bifurcations into two principal classes:

Local bifurcations, which can be analysed entirely through changes in the local stability properties of equilibria, periodic orbits or other invariant sets as parameters cross through critical thresholds; and
Global bifurcations, which often occur when larger invariant sets of the system 'collide' with each other, or with equilibria of the system. They cannot be detected purely by a stability analysis of the equilibria (fixed points).

Local bifurcations

A local bifurcation occurs when a parameter change causes the stability of an equilibrium (or fixed point) to change. In continuous systems, this corresponds to the real part of an eigenvalue of an equilibrium passing through zero. In discrete systems (those described by maps rather than ODEs), this corresponds to a fixed point having a Floquet multiplier with modulus equal to one. In both cases, the equilibrium is non-hyperbolic at the bifurcation point.
The topological changes in the phase portrait of the system can be confined to arbitrarily small neighbourhoods of the bifurcating fixed points by moving the bifurcation parameter close to the bifurcation point (hence 'local').

More technically, consider the continuous dynamical system described by the ODE

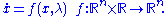
A local bifurcation occurs at

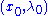if the Jacobian matrix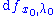

has an eigenvalue

Eigenvalue, eigenvector and eigenspace

The eigenvectors of a square matrix are the non-zero vectors that, after being multiplied by the matrix, remain parallel to the original vector. For each eigenvector, the corresponding eigenvalue is the factor by which the eigenvector is scaled when multiplied by the matrix...

with zero real part. If the eigenvalue is equal to zero, the bifurcation is a steady state bifurcation, but if the eigenvalue is non-zero but purely imaginary, this is a Hopf bifurcation

Hopf bifurcation

In the mathematical theory of bifurcations, a Hopf or Poincaré–Andronov–Hopf bifurcation, named after Henri Poincaré, Eberhard Hopf, and Aleksandr Andronov, is a local bifurcation in which a fixed point of a dynamical system loses stability as a pair of complex conjugate eigenvalues of...

.

For discrete dynamical systems, consider the system

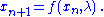
Then a local bifurcation occurs at

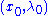if the matrix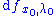

has an eigenvalue with modulus equal to one. If the eigenvalue is equal to one, the bifurcation is either a saddle-node (often called fold bifurcation in maps), transcritical or pitchfork bifurcation. If the eigenvalue is equal to −1, it is a period-doubling (or flip) bifurcation, and otherwise, it is a Hopf bifurcation.

Examples of local bifurcations include:

Saddle-node
Saddle-node bifurcation
In the mathematical area of bifurcation theory a saddle-node bifurcation, tangential bifurcation or fold bifurcation is a local bifurcation in which two fixed points of a dynamical system collide and annihilate each other. The term 'saddle-node bifurcation' is most often used in reference to...

(fold) bifurcation
Transcritical bifurcation
Transcritical bifurcation
In bifurcation theory, a field within mathematics, a transcritical bifurcation is a particular kind of local bifurcation, meaning that it is characterized by an equilibrium having an eigenvalue whose real part passes through zero....
Pitchfork bifurcation
Pitchfork bifurcation
In bifurcation theory, a field within mathematics, a pitchfork bifurcation is a particular type of local bifurcation. Pitchfork bifurcations, like Hopf bifurcations have two types - supercritical or subcritical....
Period-doubling
Period-doubling bifurcation
In mathematics, a period doubling bifurcation in a discrete dynamical system is a bifurcation in which the system switches to a new behavior with twice the period of the original system...

(flip) bifurcation
Hopf bifurcation
Hopf bifurcation
In the mathematical theory of bifurcations, a Hopf or Poincaré–Andronov–Hopf bifurcation, named after Henri Poincaré, Eberhard Hopf, and Aleksandr Andronov, is a local bifurcation in which a fixed point of a dynamical system loses stability as a pair of complex conjugate eigenvalues of...
Neimark (secondary Hopf) bifurcation

Global bifurcations

Global bifurcations occur when 'larger' invariant sets, such as periodic orbits, collide with equilibria. This causes changes in the topology of the trajectories in the phase space which cannot be confined to a small neighbourhood, as is the case with local bifurcations. In fact, the changes in topology extend out to an arbitrarily large distance (hence 'global').

Examples of global bifurcations include:

Homoclinic bifurcation
Homoclinic bifurcation
In mathematics, a homoclinic bifurcation is a global bifurcation which often occurs when a periodic orbit collides with a saddle point.The image below shows a phase portrait before, at, and after a homoclinic bifurcation in 2D. The periodic orbit grows until it collides with the saddle point...

in which a limit cycle collides with a saddle point
Saddle point
In mathematics, a saddle point is a point in the domain of a function that is a stationary point but not a local extremum. The name derives from the fact that in two dimensions the surface resembles a saddle that curves up in one direction, and curves down in a different direction...

.
Heteroclinic bifurcation
Heteroclinic bifurcation
In mathematics, particularly dynamical systems, a heteroclinic bifurcation is a global bifurcation involving a heteroclinic cycle. Heteroclinic bifurcations come in two types, resonance bifurcations, and transverse bifurcations...

in which a limit cycle collides with two or more saddle points.
Infinite-period bifurcation
Infinite-period bifurcation
In mathematics, an infinite-period bifurcation is a global bifurcation that can occur when two fixed points emerge on a limit cycle. As the limit of a parameter approaches a certain critical value, the speed of the oscillation slows down and the period approaches infinity. The infinite-period...

in which a stable node and saddle point simultaneously occur on a limit cycle.
Blue sky catastrophe
Blue sky catastrophe
The blue sky catastrophe is a type of bifurcation of a periodic orbit. In other words, it describes a sort of behaviour stable solutions of a set of differential equations can undergo as the equations are gradually changed...

in which a limit cycle collides with a nonhyperbolic cycle.

Global bifurcations can also involve more complicated sets such as chaotic attractors (e.g. crises

Crisis (dynamical systems)

In applied mathematics, in the theory of dynamical systems, a crisis is the sudden appearance or disappearance of a strange attractor as the parameters of a dynamical system are varied. This global bifurcation occurs when a chaotic attractor comes into contact with an unstable periodic orbit or its...

Codimension of a bifurcation

The codimension of a bifurcation is the number of parameters which must be varied for the bifurcation to occur. This corresponds to the codimension of the parameter set for which the bifurcation occurs within the full space of parameters. Saddle-node bifurcations and Hopf bifurcations are the only generic local bifurcations which are really codimension-one (the others all having higher codimension). However, often transcritical and pitchfork bifurcations are also often thought of as codimension-one, because the normal forms can be written with only one parameter.

An example of a well-studied codimension-two bifurcation is the Bogdanov–Takens bifurcation

Bogdanov-Takens bifurcation

In bifurcation theory, a field within mathematics, a Bogdanov-Takens bifurcation is a well-studied example of a bifurcation with co-dimension two, meaning that two parameters must be varied for the bifurcation to occur...

Applications in semiclassical and quantum physics

Bifurcation theory has been applied to connect quantum systems to the dynamics of their classical analogues in atomic systems, molecular systems, and resonant tunneling diodes. Bifurcation theory has also been applied to the study of laser dynamics and a number of theoretical examples which are difficult to access experimentally such as the kicked top and coupled quantum wells. The dominant reason for the link between quantum systems and bifurcations in the classical equations of motion is that at bifurcations, the signature of classical orbits becomes large, as Martin Gutzwiller

Martin Gutzwiller

Martin C. Gutzwiller is a physicist. He is known for the invention of the variational wave-function describing electrons with strong localized interactions , for the first investigation of relations between classical and quantum mechanics in chaotic systems , as well as new solutions to...

points out in his classic work on quantum chaos

Quantum chaos

Quantum chaos is a branch of physics which studies how chaotic classical dynamical systems can be described in terms of quantum theory. The primary question that quantum chaos seeks to answer is, "What is the relationship between quantum mechanics and classical chaos?" The correspondence principle...

. Many kinds of bifurcations have been studied with regard to links between classical and quantum dynamics including saddle node bifurcations, Hopf bifurcations, umbilic bifurcations, period doubling bifurcations, reconnection bifurcations, tangent bifurcations, and cusp bifurcations.

Bifurcation types

Local bifurcations

Global bifurcations

Codimension of a bifurcation

Applications in semiclassical and quantum physics

See also