Attractor - AbsoluteAstronomy.com

An attractor is a set towards which a dynamical system

Dynamical system

A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...

evolves over time. That is, points that get close enough to the attractor remain close even if slightly disturbed. Geometrically

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, an attractor can be a point

Point (geometry)

In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...

, a curve

Curve

In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...

, a manifold

Manifold

In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....

, or even a complicated set with a fractal

Fractal

A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...

structure known as a strange attractor. Describing the attractors of chaotic dynamical systems has been one of the achievements of chaos theory

Chaos theory

Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...

.

A trajectory

Trajectory

A trajectory is the path that a moving object follows through space as a function of time. The object might be a projectile or a satellite, for example. It thus includes the meaning of orbit—the path of a planet, an asteroid or a comet as it travels around a central mass...

of the dynamical system in the attractor does not have to satisfy any special constraints except for remaining on the attractor. The trajectory may be periodic

Periodic function

In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...

or chaotic

Chaos theory

or of any other type. If this condition is met, but the flow in the neighbourhood is away from the set, the set is called a repeller (or repellor).

Motivation

A dynamical system

Dynamical system

is generally described by one or more differential or difference equations. The equations of a given dynamic system specify its behavior over any given short period of time. To determine the system's behavior for a longer period, it is necessary to integrate

Integral

Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...

the equations, either through analytical means or through iteration, often with the aid of computers.

Dynamical systems in the physical world tend to be dissipative

Dissipative system

A dissipative system is a thermodynamically open system which is operating out of, and often far from, thermodynamic equilibrium in an environment with which it exchanges energy and matter....

: if it were not for some driving force, the motion would cease. (Dissipation may come from internal friction

Friction

Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...

, thermodynamic losses

Thermodynamics

Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...

, or loss of material, among many causes.) The dissipation and the driving force tend to combine to kill out initial transients and settle the system into its typical behavior. This one part of the phase space

Phase space

In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...

of the dynamical system corresponding to the typical behavior is the attracting section or attractee.

Invariant sets and limit set

Limit set

In mathematics, especially in the study of dynamical systems, a limit set is the state a dynamical system reaches after an infinite amount of time has passed, by either going forward or backwards in time...

s are similar to the attractor concept. An invariant set is a set that evolves to itself under the dynamics. Attractors may contain invariant sets. A limit set is a set of points such that there exists some initial state that ends up arbitrarily close to the limit set (i.e. to each point of the set) as time goes to infinity. Attractors are limit sets, but not all limit sets are attractors: It is possible to have some points of a system converge to a limit set, but different points when perturbed slightly off the limit set may get knocked off and never return to the vicinity of the limit set.

For example, the damped pendulum has two invariant points: the point

of minimum height and the point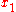

of maximum height. The point

is also a limit set, as trajectories converge to it; the point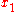

is not a limit set. Because of the dissipation, the point

is also an attractor. If there were no dissipation,

would not be an attractor.

Mathematical definition

Let f(t, •) be a function which specifies the dynamics of the system. That is, if a is a point in the phase space, representing the initial state of the system, then f(0, a) = a and, for a positive value of t, f(t, a) is the result of the evolution of this state after t units of time. For example, if the system is a free particle in one dimension then the phase space is the plane R² with coordinates (x,v), where x is the position of the particle and v is its velocity, and the evolution is given by

An attractor is a subset

Subset

In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...

A of the phase space

Phase space

characterized by the following three conditions:

A is forward invariant under f: if a is an element of A then so is f(t,a), for all t > 0.

There exists a neighborhood
Neighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...

of A, called the basin of attraction for A and denoted B(A), which consists of all points b that "enter A in the limit t → ∞". More formally, B(A) is the set of all points b in the phase space with the following property:

For any open neighborhood N of A, there is a positive constant T such that f(t,b) ∈ N for all real t > T.

There is no proper subset of A having the first two properties.

Since the basin of attraction contains an open set

Open set

The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...

containing A, every point that is sufficiently close to A is attracted to A. The definition of an attractor uses a metric

Metric space

In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...

on the phase space, but the resulting notion usually depends only on the topology of the phase space. In the case of Rⁿ, the Euclidean norm is typically used.

Many other definitions of attractor occur in the literature. For example, some authors require that an attractor have positive measure

Measure (mathematics)

In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...

(preventing a point from being an attractor), others relax the requirement that B(A) be a neighborhood.

Types of attractors

Attractors are parts of the phase space of the dynamical system. Until the 1960s, as evidenced by textbooks of that era, attractors were thought of as being geometrical subsets of the phase space: points

Point (geometry)

, lines

Line (mathematics)

The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...

, surface

Surface

In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...

s, volume

Volume

Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....

s. The (topologically

Topology

Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...

) wild sets that had been observed were thought to be fragile anomalies. Stephen Smale

Stephen Smale

Steven Smale a.k.a. Steve Smale, Stephen Smale is an American mathematician from Flint, Michigan. He was awarded the Fields Medal in 1966, and spent more than three decades on the mathematics faculty of the University of California, Berkeley .-Education and career:He entered the University of...

was able to show that his horseshoe map

Horseshoe map

In the mathematics of chaos theory, a horseshoe map is any member of a class of chaotic maps of the square into itself. It is a core example in the study of dynamical systems. The map was introduced by Stephen Smale while studying the behavior of the orbits of the van der Pol oscillator...

was robust

Structural stability

In mathematics, structural stability is a fundamental property of a dynamical system which means that the qualitative behavior of the trajectories is unaffected by C1-small perturbations....

and that its attractor had the structure of a Cantor set

Cantor set

In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....

.

Two simple attractors are the fixed point and the limit cycle. There can be many other geometrical sets that are attractors. When these sets (or the motions on them), are hard to describe, then the attractor is a strange attractor, as described in the section below.

Fixed point

A fixed point

Fixed point (mathematics)

In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...

is a point of a function that does not change under some transformation. If we regard the evolution of a dynamical system as a series of transformations, then there may or may not be a point which remains fixed under the whole series of transformation. In general there would not be such a point, but there may be one. The final state that a dynamical system evolves towards, such as the final states of a falling pebble, a damped pendulum, or the water in a glass corresponds to a fixed point of the evolution function, and will occur at the attractor, but the two concepts are not equivalent. A marble rolling around in a basin may have a fixed point in phase space even if it doesn't in physical space. Once it has lost momentum and settled into the bottom of the bowl it then has a fixed point in physical space, phase space, and is located at the attractor for that system.

Limit cycle

See main article limit cycle

A limit cycle is a periodic orbit of the system that is isolated

Isolated point

In topology, a branch of mathematics, a point x of a set S is called an isolated point of S, if there exists a neighborhood of x not containing other points of S.In particular, in a Euclidean space ,...

. Examples include the swings of a pendulum clock

Pendulum clock

A pendulum clock is a clock that uses a pendulum, a swinging weight, as its timekeeping element. The advantage of a pendulum for timekeeping is that it is a resonant device; it swings back and forth in a precise time interval dependent on its length, and resists swinging at other rates...

, the tuning circuit of a radio, and the heartbeat while resting. The ideal pendulum is not an example because its orbits are not isolated. In phase space of the ideal pendulum, near any point of a periodic orbit there is another point that belongs to a different periodic orbit.

Limit tori

There may be more than one frequency in the periodic trajectory of the system through the state of a limit cycle. If two of these frequencies form an irrational fraction

Irrational number

In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....

(i.e. they are incommensurate

Commensurability (mathematics)

In mathematics, two non-zero real numbers a and b are said to be commensurable if a/b is a rational number.-History of the concept:...

), the trajectory is no longer closed, and the limit cycle becomes a limit torus

Torus

In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...

. We call this kind of attractor

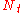-torus if there are

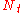incommensurate frequencies. For example here is a 2-torus:

A time series corresponding to this attractor is a quasiperiodic series: A discretely sampled sum of

periodic functions (not necessarily sine

Sine

In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....

waves) with incommensurate frequencies. Such a time series does not have a strict periodicity, but its power spectrum still consists only of sharp lines.

Strange attractor

An attractor is informally described as strange if it has non-integer

Hausdorff dimension

thumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...

dimension. This is often the case when the dynamics on it are chaotic

Chaos theory

, but there exists also strange attractors that are not chaotic. The term was coined by David Ruelle

David Ruelle

David Pierre Ruelle is a Belgian-French mathematical physicist. He has worked on statistical physics and dynamical systems. With Floris Takens he coined the term strange attractor, and founded a new theory of turbulence...

and Floris Takens

Floris Takens

Floris Takens was a Dutch mathematician known for contributions to the theory of chaotic dynamical systems.Together with David Ruelle he predicted that fluid turbulence could develop through a strange attractor, a term they coined, as opposed to the then-prevailing theory of accretion of modes....

to describe the attractor that resulted from a series of bifurcations

Bifurcation theory

Bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations...

of a system describing fluid flow.
Strange attractors are often differentiable in a few directions, but some are like a Cantor dust, and therefore not differentiable.

Examples of strange attractors include the Hénon attractor, Rössler attractor

Rössler attractor

The Rössler attractor is the attractor for the Rössler system, a system of three non-linear ordinary differential equations. These differential equations define a continuous-time dynamical system that exhibits chaotic dynamics associated with the fractal properties of the attractor...

, Lorenz attractor

Lorenz attractor

The Lorenz attractor, named for Edward N. Lorenz, is an example of a non-linear dynamic system corresponding to the long-term behavior of the Lorenz oscillator. The Lorenz oscillator is a 3-dimensional dynamical system that exhibits chaotic flow, noted for its lemniscate shape...

, Tamari attractor

Tamari Attractor

In the mathematics of dynamical systems, the Tamari attractor, named for , is a 3-dimensional attractor evolving from the dynamic system associated with the theory of a country's economics. This dynamical system is a set of partial differential equations that, by the theory of economics developed...

Partial differential equations

Parabolic partial differential equation

A parabolic partial differential equation is a type of second-order partial differential equation , describing a wide family of problems in science including heat diffusion, ocean acoustic propagation, in physical or mathematical systems with a time variable, and which behave essentially like heat...

s may have finite-dimensional attractors. The diffusive part of the equation damps higher frequencies and in some cases leads to a global attractor. The Ginzburg–Landau, the Kuramoto–Sivashinsky, and the two-dimensional, forced Navier–Stokes equations are all known to have global attractors of finite dimension.

For the three-dimensional, incompressible Navier–Stokes equation with periodic boundary conditions, if it has a global attractor, then this attractor will be of finite dimensions.

Numerical localization (visualization) of attractors

From computation point of view, attractors can be naturally regarded as self-exciting attractors or
hidden attractors.
Self-exciting attractors can be localized numerically by standard computational procedure, in which after transient process a trajectory, started from a point of unstable manifold in a small neighborhood of unstable equilibrium, reaches an attractor and computes it (like classical attractors in Van der Pol, Beluosov–Zhabotinsky, Lorenz

Lorenz attractor

, and many others dynamical systems).
While basin of attraction

Basin

Basin may refer to:* Basin , a poem about Charlemagne's childhood* basin , the area of a drydock which can be flooded and drained* basin of attraction , an area of a nonlinear system with an attractor...

of hidden attractors does not contain neighborhoods of equilibria, and therefore hidden attractor cannot be localized by standard computational procedure.

External links

Basin of attraction on Scholarpedia
A gallery of trigonometric strange attractors
Double scroll attractor Chua's circuit simulation
A gallery of polynomial strange attractors
Animated Pickover Strange Attractors
Chaoscope, a 3D Strange Attractor rendering freeware
1D, 2D and 3D of strange attractors, include Tamari Attractor
Research abstract and [ftp://ftp2.sco.com/pub/skunkware/src/x11/misc/mathrec-1.1c.tar.gz software laboratory]
Online strange attractors generator
Tamari attractor

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.

Motivation

Mathematical definition

Types of attractors

Fixed point

Limit cycle

Limit tori

Strange attractor

Partial differential equations

Numerical localization (visualization) of attractors

See also

Further reading

External links