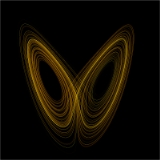
Dynamical system
Encyclopedia

Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
describes the time dependence of a point in a geometrical space
Configuration space
- Configuration space in physics :In classical mechanics, the configuration space is the space of possible positions that a physical system may attain, possibly subject to external constraints...
. Examples include the mathematical model
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
s that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a lake.
At any given time a dynamical system has a state given by a set of real numbers (a vector
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
) that can be represented by a point
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
in an appropriate state space
State space
In the theory of discrete dynamical systems, a state space is a directed graph where each possible state of a dynamical system is represented by a vertex, and there is a directed edge from a to b if and only if ƒ = b where the function f defines the dynamical system.State spaces are...
(a geometrical manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
). Small changes in the state of the system create small changes in the numbers. The evolution rule of the dynamical system is a fixed rule
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
that describes what future states follow from the current state. The rule is deterministic
Deterministic system (mathematics)
In mathematics, a deterministic system is a system in which no randomness is involved in the development of future states of the system. A deterministic model will thus always produce the same output from a given starting condition or initial state.-Examples:...
; in other words, for a given time interval only one future state follows from the current state.
Overview
The concept of a dynamical system has its origins in Newtonian mechanics. There, as in other natural sciences and engineering disciplines, the evolution rule of dynamical systems is given implicitly by a relation that gives the state of the system only a short time into the future. (The relation is either a differential equationDifferential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
, difference equation
Recurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
or other time scale
Time scale calculus
In mathematics, time-scale calculus is a unification of the theory of difference equations with that of differential equations, unifying integral and differential calculus with the calculus of finite differences, offering a formalism for studying hybrid discrete–continuous dynamical systems...
.) To determine the state for all future times requires iterating the relation many times—each advancing time a small step. The iteration procedure is referred to as solving the system or integrating the system. Once the system can be solved, given an initial point it is possible to determine all its future positions, a collection of points known as a trajectory
Trajectory
A trajectory is the path that a moving object follows through space as a function of time. The object might be a projectile or a satellite, for example. It thus includes the meaning of orbit—the path of a planet, an asteroid or a comet as it travels around a central mass...
or orbit
Orbit (dynamics)
In mathematics, in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the...
.
Before the advent of fast computing machines
Computer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
, solving a dynamical system required sophisticated mathematical techniques and could be accomplished only for a small class of dynamical systems. Numerical methods implemented on electronic computing machines have simplified the task of determining the orbits of a dynamical system.
For simple dynamical systems, knowing the trajectory is often sufficient, but most dynamical systems are too complicated to be understood in terms of individual trajectories. The difficulties arise because:
- The systems studied may only be known approximately—the parameters of the system may not be known precisely or terms may be missing from the equations. The approximations used bring into question the validity or relevance of numerical solutions. To address these questions several notions of stability have been introduced in the study of dynamical systems, such as Lyapunov stabilityLyapunov stabilityVarious types of stability may be discussed for the solutions of differential equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. This may be discussed by the theory of Lyapunov...
or structural stabilityStructural stabilityIn mathematics, structural stability is a fundamental property of a dynamical system which means that the qualitative behavior of the trajectories is unaffected by C1-small perturbations....
. The stability of the dynamical system implies that there is a class of models or initial conditions for which the trajectories would be equivalent. The operation for comparing orbits to establish their equivalenceEquivalenceEquivalence or equivalent may refer to:*In chemistry:**Equivalent **Equivalence point**Equivalent weight*In computing:**Turing equivalence *In ethics:**Moral equivalence*In history:...
changes with the different notions of stability. - The type of trajectory may be more important than one particular trajectory. Some trajectories may be periodic, whereas others may wander through many different states of the system. Applications often require enumerating these classes or maintaining the system within one class. Classifying all possible trajectories has led to the qualitative study of dynamical systems, that is, properties that do not change under coordinate changes. Linear dynamical systemLinear dynamical systemLinear dynamical systems are a special type of dynamical system where the equation governing the system's evolution is linear. While dynamical systems in general do not have closed-form solutions, linear dynamical systems can be solved exactly, and they have a rich set of mathematical properties...
s and systems that have two numbers describing a statePoincaré–Bendixson theoremIn mathematics, the Poincaré–Bendixson theorem is a statement about the long-term behaviour of orbits of continuous dynamical systems on the plane.-Theorem:...
are examples of dynamical systems where the possible classes of orbits are understood. - The behavior of trajectories as a function of a parameter may be what is needed for an application. As a parameter is varied, the dynamical systems may have bifurcation pointsBifurcation theoryBifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations...
where the qualitative behavior of the dynamical system changes. For example, it may go from having only periodic motions to apparently erratic behavior, as in the transition to turbulence of a fluidTurbulenceIn fluid dynamics, turbulence or turbulent flow is a flow regime characterized by chaotic and stochastic property changes. This includes low momentum diffusion, high momentum convection, and rapid variation of pressure and velocity in space and time...
. - The trajectories of the system may appear erratic, as if random. In these cases it may be necessary to compute averages using one very long trajectory or many different trajectories. The averages are well defined for ergodic systemsErgodic theoryErgodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
and a more detailed understanding has been worked out for hyperbolic systemsAnosov diffeomorphismIn mathematics, more particularly in the fields of dynamical systems and geometric topology, an Anosov map on a manifold M is a certain type of mapping, from M to itself, with rather clearly marked local directions of 'expansion' and 'contraction'. Anosov systems are a special case of Axiom A...
. Understanding the probabilistic aspects of dynamical systems has helped establish the foundations of statistical mechanicsStatistical mechanicsStatistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
and of chaosChaos theoryChaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
.
It was in the work of Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
that these dynamical systems themes developed.
Basic definitions
A dynamical system is a manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
M called the phase (or state) space endowed with a family of smooth evolution functions Φ t that for any element of
 , the time, map a point of the phase space back into the phase space. The notion of smoothness changes with applications and the type of manifold. There are several choices for the set T. When T is taken to be the reals, the dynamical system is called a flow
, the time, map a point of the phase space back into the phase space. The notion of smoothness changes with applications and the type of manifold. There are several choices for the set T. When T is taken to be the reals, the dynamical system is called a flowFlow (mathematics)
In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
; and if T is restricted to the non-negative reals, then the dynamical system is a semi-flow. When T is taken to be the integers, it is a cascade or a map; and the restriction to the non-negative integers is a semi-cascade.
Examples
The evolution function Φ t is often the solution of a differential equation of motionThe equation gives the time derivative, represented by the dot, of a trajectory x(t) on the phase space starting at some point x0. The vector field v(x) is a smooth function that at every point of the phase space M provides the velocity vector of the dynamical system at that point. (These vectors are not vectors in the phase space M, but in the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
TxM of the point x.) Given a smooth Φ t, an autonomous vector field can be derived from it.
There is no need for higher order derivatives in the equation, nor for time dependence in v(x) because these can be eliminated by considering systems of higher dimensions. Other types of differential equations can be used to define the evolution rule:
is an example of an equation that arises from the modeling of mechanical systems with complicated constraints.
The differential equations determining the evolution function Φ t are often ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s: in this case the phase space M is a finite dimensional manifold. Many of the concepts in dynamical systems can be extended to infinite-dimensional manifolds—those that are locally Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
s—in which case the differential equations are partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s. In the late 20th century the dynamical system perspective to partial differential equations started gaining popularity.
Linear dynamical systems
Linear dynamical systems can be solved in terms of simple functions and the behavior of all orbits classified. In a linear system the phase space is the N-dimensional Euclidean space, so any point in phase space can be represented by a vector with N numbers. The analysis of linear systems is possible because they satisfy a superposition principle: if u(t) and w(t) satisfy the differential equation for the vector field (but not necessarily the initial condition), then so will u(t) + w(t).Flows
For a flowFlow (mathematics)
In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
, the vector field Φ(x) is a linear function of the position in the phase space, that is,
with A a matrix, b a vector of numbers and x the position vector. The solution to this system can be found by using the superposition principle (linearity).
The case b ≠ 0 with A = 0 is just a straight line in the direction of b:
When b is zero and A ≠ 0 the origin is an equilibrium (or singular) point of the flow, that is, if x0 = 0, then the orbit remains there.
For other initial conditions, the equation of motion is given by the exponential of a matrix
Matrix exponential
In mathematics, the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. Abstractly, the matrix exponential gives the connection between a matrix Lie algebra and the corresponding Lie group....
: for an initial point x0,
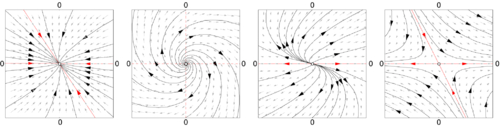
When b = 0, the eigenvalues of A determine the structure of the phase space. From the eigenvalues and the eigenvectors of A it is possible to determine if an initial point will converge or diverge to the equilibrium point at the origin.
The distance between two different initial conditions in the case A ≠ 0 will change exponentially in most cases, either converging exponentially fast towards a point, or diverging exponentially fast. Linear systems display sensitive dependence on initial conditions in the case of divergence. For nonlinear systems this is one of the (necessary but not sufficient) conditions for chaotic behavior
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
.
Maps
A discrete-time, affineAffine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
dynamical system has the form
with A a matrix and b a vector. As in the continuous case, the change of coordinates x → x + (1 − A) –1b removes the term b from the equation. In the new coordinate system, the origin is a fixed point of the map and the solutions are of the linear system A nx0.
The solutions for the map are no longer curves, but points that hop in the phase space. The orbits are organized in curves, or fibers, which are collections of points that map into themselves under the action of the map.
As in the continuous case, the eigenvalues and eigenvectors of A determine the structure of phase space. For example, if u1 is an eigenvector of A, with a real eigenvalue smaller than one, then the straight lines given by the points along α u1, with α ∈ R, is an invariant curve of the map. Points in this straight line run into the fixed point.
There are also many other discrete dynamical systems.
Local dynamics
The qualitative properties of dynamical systems do not change under a smooth change of coordinates (this is sometimes taken as a definition of qualitative): a singular point of the vector field (a point where v(x) = 0) will remain a singular point under smooth transformations; a periodic orbit is a loop in phase space and smooth deformations of the phase space cannot alter it being a loop. It is in the neighborhood of singular points and periodic orbits that the structure of a phase space of a dynamical system can be well understood. In the qualitative study of dynamical systems, the approach is to show that there is a change of coordinates (usually unspecified, but computable) that makes the dynamical system as simple as possible.Rectification
A flow in most small patches of the phase space can be made very simple. If y is a point where the vector field v(y) ≠ 0, then there is a change of coordinates for a region around y where the vector field becomes a series of parallel vectors of the same magnitude. This is known as the rectification theorem.The rectification theorem says that away from singular points the dynamics of a point in a small patch is a straight line. The patch can sometimes be enlarged by stitching several patches together, and when this works out in the whole phase space M the dynamical system is integrable. In most cases the patch cannot be extended to the entire phase space. There may be singular points in the vector field (where v(x) = 0); or the patches may become smaller and smaller as some point is approached. The more subtle reason is a global constraint, where the trajectory starts out in a patch, and after visiting a series of other patches comes back to the original one. If the next time the orbit loops around phase space in a different way, then it is impossible to rectify the vector field in the whole series of patches.
Near periodic orbits
In general, in the neighborhood of a periodic orbit the rectification theorem cannot be used. Poincaré developed an approach that transforms the analysis near a periodic orbit to the analysis of a map. Pick a point x0 in the orbit γ and consider the points in phase space in that neighborhood that are perpendicular to v(x0). These points are a Poincaré section S(γ, x0), of the orbit. The flow now defines a map, the Poincaré mapPoincaré map
In mathematics, particularly in dynamical systems, a first recurrence map or Poincaré map, named after Henri Poincaré, is the intersection of a periodic orbit in the state space of a continuous dynamical system with a certain lower dimensional subspace, called the Poincaré section, transversal to...
F : S → S, for points starting in S and returning to S. Not all these points will take the same amount of time to come back, but the times will be close to the time it takes x0.
The intersection of the periodic orbit with the Poincaré section is a fixed point of the Poincaré map F. By a translation, the point can be assumed to be at x = 0. The Taylor series of the map is F(x) = J · x + O(x2), so a change of coordinates h can only be expected to simplify F to its linear part
This is known as the conjugation equation. Finding conditions for this equation to hold has been one of the major tasks of research in dynamical systems. Poincaré first approached it assuming all functions to be analytic and in the process discovered the non-resonant condition. If λ1, ..., λν are the eigenvalues of J they will be resonant if one eigenvalue is an integer linear combination of two or more of the others. As terms of the form λi – ∑ (multiples of other eigenvalues) occurs in the denominator of the terms for the function h, the non-resonant condition is also known as the small divisor problem.
Conjugation results
The results on the existence of a solution to the conjugation equation depend on the eigenvalues of J and the degree of smoothness required from h. As J does not need to have any special symmetries, its eigenvalues will typically be complex numbers. When the eigenvalues of J are not in the unit circle, the dynamics near the fixed point x0 of F is called hyperbolic and when the eigenvalues are on the unit circle and complex, the dynamics is called elliptic.In the hyperbolic case the Hartman–Grobman theorem gives the conditions for the existence of a continuous function that maps the neighborhood of the fixed point of the map to the linear map J · x. The hyperbolic case is also structurally stable. Small changes in the vector field will only produce small changes in the Poincaré map and these small changes will reflect in small changes in the position of the eigenvalues of J in the complex plane, implying that the map is still hyperbolic.
The Kolmogorov–Arnold–Moser (KAM)
Kolmogorov–Arnold–Moser theorem
The Kolmogorov–Arnold–Moser theorem is a result in dynamical systems about the persistence of quasi-periodic motions under small perturbations. The theorem partly resolves the small-divisor problem that arises in the perturbation theory of classical mechanics....
theorem gives the behavior near an elliptic point.
Bifurcation theory
When the evolution map Φt (or the vector fieldVector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
it is derived from) depends on a parameter μ, the structure of the phase space will also depend on this parameter. Small changes may produce no qualitative changes in the phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
until a special value μ0 is reached. At this point the phase space changes qualitatively and the dynamical system is said to have gone through a bifurcation.
Bifurcation theory considers a structure in phase space (typically a fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
, a periodic orbit, or an invariant torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
) and studies its behavior as a function of the parameter μ. At the bifurcation point the structure may change its stability, split into new structures, or merge with other structures. By using Taylor series approximations of the maps and an understanding of the differences that may be eliminated by a change of coordinates, it is possible to catalog the bifurcations of dynamical systems.
The bifurcations of a hyperbolic fixed point x0 of a system family Fμ can be characterized by the eigenvalues of the first derivative of the system DFμ(x0) computed at the bifurcation point. For a map, the bifurcation will occur when there are eigenvalues of DFμ on the unit circle. For a flow, it will occur when there are eigenvalues on the imaginary axis. For more information, see the main article on Bifurcation theory
Bifurcation theory
Bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations...
.
Some bifurcations can lead to very complicated structures in phase space. For example, the Ruelle–Takens scenario describes how a periodic orbit bifurcates into a torus and the torus into a strange attractor. In another example, Feigenbaum period-doubling
Bifurcation diagram
In mathematics, particularly in dynamical systems, a bifurcation diagram shows the possible long-term values of a system as a function of a bifurcation parameter in the system...
describes how a stable periodic orbit goes through a series of period-doubling bifurcation
Period-doubling bifurcation
In mathematics, a period doubling bifurcation in a discrete dynamical system is a bifurcation in which the system switches to a new behavior with twice the period of the original system...
s.
Ergodic systems
In many dynamical systems it is possible to choose the coordinates of the system so that the volume (really a ν-dimensional volume) in phase space is invariant. This happens for mechanical systems derived from Newton's laws as long as the coordinates are the position and the momentum and the volume is measured in units of (position) × (momentum). The flow takes points of a subset A into the points Φ t(A) and invariance of the phase space means thatIn the Hamiltonian formalism
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
, given a coordinate it is possible to derive the appropriate (generalized) momentum such that the associated volume is preserved by the flow. The volume is said to be computed by the Liouville measure
Liouville's theorem (Hamiltonian)
In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical and Hamiltonian mechanics...
.
In a Hamiltonian system not all possible configurations of position and momentum can be reached from an initial condition. Because of energy conservation, only the states with the same energy as the initial condition are accessible. The states with the same energy form an energy shell Ω, a sub-manifold of the phase space. The volume of the energy shell, computed using the Liouville measure, is preserved under evolution.
For systems where the volume is preserved by the flow, Poincaré discovered the recurrence theorem
Poincaré recurrence theorem
In mathematics, the Poincaré recurrence theorem states that certain systems will, after a sufficiently long time, return to a state very close to the initial state. The Poincaré recurrence time is the length of time elapsed until the recurrence. The result applies to physical systems in which...
: Assume the phase space has a finite Liouville volume and let F be a phase space volume-preserving map and A a subset of the phase space. Then almost every point of A returns to A infinitely often. The Poincaré recurrence theorem was used by Zermelo to object to Boltzmann's derivation of the increase in entropy in a dynamical system of colliding atoms.
One of the questions raised by Boltzmann's work was the possible equality between time averages and space averages, what he called the ergodic hypothesis
Ergodic hypothesis
In physics and thermodynamics, the ergodic hypothesis says that, over long periods of time, the time spent by a particle in some region of the phase space of microstates with the same energy is proportional to the volume of this region, i.e., that all accessible microstates are equiprobable over a...
. The hypothesis states that the length of time a typical trajectory spends in a region A is vol(A)/vol(Ω).
The ergodic hypothesis turned out not to be the essential property needed for the development of statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
and a series of other ergodic-like properties were introduced to capture the relevant aspects of physical systems. Koopman
Bernard Koopman
Bernard Osgood Koopman was a French-born American mathematician, known for his work in ergodic theory, the foundations of probability, statistical theory and operations research....
approached the study of ergodic systems by the use of functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
. An observable a is a function that to each point of the phase space associates a number (say instantaneous pressure, or average height). The value of an observable can be computed at another time by using the evolution function φ t. This introduces an operator U t, the transfer operator
Transfer operator
In mathematics, the transfer operator encodes information about an iterated map and is frequently used to study the behavior of dynamical systems, statistical mechanics, quantum chaos and fractals...
,
By studying the spectral properties of the linear operator U it becomes possible to classify the ergodic properties of Φ t. In using the Koopman approach of considering the action of the flow on an observable function, the finite-dimensional nonlinear problem involving Φ t gets mapped into an infinite-dimensional linear problem involving U.
The Liouville measure restricted to the energy surface Ω is the basis for the averages computed in equilibrium statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
. An average in time along a trajectory is equivalent to an average in space computed with the Boltzmann factor exp(−βH). This idea has been generalized by Sinai, Bowen, and Ruelle (SRB) to a larger class of dynamical systems that includes dissipative systems. SRB measures replace the Boltzmann factor and they are defined on attractors of chaotic systems.
Nonlinear dynamical systems and chaos
Simple nonlinear dynamical systems and even piecewise linear systems can exhibit a completely unpredictable behavior, which might seem to be random, despite the fact that they are fundamentally deterministic. This seemingly unpredictable behavior has been called chaosChaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
. Hyperbolic systems
Anosov diffeomorphism
In mathematics, more particularly in the fields of dynamical systems and geometric topology, an Anosov map on a manifold M is a certain type of mapping, from M to itself, with rather clearly marked local directions of 'expansion' and 'contraction'. Anosov systems are a special case of Axiom A...
are precisely defined dynamical systems that exhibit the properties ascribed to chaotic systems. In hyperbolic systems the tangent space perpendicular to a trajectory can be well separated into two parts: one with the points that converge towards the orbit (the stable manifold) and another of the points that diverge from the orbit (the unstable manifold).
This branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
deals with the long-term qualitative behavior of dynamical systems. Here, the focus is not on finding precise solutions to the equations defining the dynamical system (which is often hopeless), but rather to answer questions like "Will the system settle down to a steady state in the long term, and if so, what are the possible attractor
Attractor
An attractor is a set towards which a dynamical system evolves over time. That is, points that get close enough to the attractor remain close even if slightly disturbed...
s?" or "Does the long-term behavior of the system depend on its initial condition?"
Note that the chaotic behavior of complex systems is not the issue. Meteorology
Meteorology
Meteorology is the interdisciplinary scientific study of the atmosphere. Studies in the field stretch back millennia, though significant progress in meteorology did not occur until the 18th century. The 19th century saw breakthroughs occur after observing networks developed across several countries...
has been known for years to involve complex—even chaotic—behavior. Chaos theory has been so surprising because chaos can be found within almost trivial systems. The logistic map
Logistic map
The logistic map is a polynomial mapping of degree 2, often cited as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations...
is only a second-degree polynomial; the horseshoe map
Horseshoe map
In the mathematics of chaos theory, a horseshoe map is any member of a class of chaotic maps of the square into itself. It is a core example in the study of dynamical systems. The map was introduced by Stephen Smale while studying the behavior of the orbits of the van der Pol oscillator...
is piecewise linear.
Geometrical definition
A dynamical system is the tuple , with
, with  a manifold (locally a Banach space or Euclidean space),
a manifold (locally a Banach space or Euclidean space),  the domain for time (non-negative reals, the integers, ...) and
the domain for time (non-negative reals, the integers, ...) and  an evolution rule t → f t (with
an evolution rule t → f t (with  ) such that f t is a diffeomorphism
) such that f t is a diffeomorphismDiffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
of the manifold to itself. So, f is a mapping of the time-domain
 into the space of diffeomorphisms of the manifold to itself. In other terms, f(t) is a diffeomorphism, for every time t in the domain
into the space of diffeomorphisms of the manifold to itself. In other terms, f(t) is a diffeomorphism, for every time t in the domain  .
.Measure theoretical definition
- See main article Measure-preserving dynamical systemMeasure-preserving dynamical systemIn mathematics, a measure-preserving dynamical system is an object of study in the abstract formulation of dynamical systems, and ergodic theory in particular.-Definition:...
.
A dynamical system may be defined formally, as a measure-preserving transformation of a sigma-algebra
Sigma-algebra
In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
, the quadruplet
 . Here, X is a set, and Σ is a sigma-algebra
. Here, X is a set, and Σ is a sigma-algebraSigma-algebra
In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
on X, so that the pair
 is a measurable space. μ is a finite measure
is a measurable space. μ is a finite measureMeasure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
on the sigma-algebra, so that the triplet
 is a probability space. A map
is a probability space. A map  is said to be Σ-measurable
is said to be Σ-measurableMeasurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
if and only if, for every
 , one has
, one has  . A map
. A map  is said to preserve the measure if and only if, for every
is said to preserve the measure if and only if, for every  , one has
, one has  . Combining the above, a map
. Combining the above, a map  is said to be a measure-preserving transformation of X , if it is a map from X to itself, it is Σ-measurable, and is measure-preserving. The quadruple
is said to be a measure-preserving transformation of X , if it is a map from X to itself, it is Σ-measurable, and is measure-preserving. The quadruple  , for such a
, for such a  , is then defined to be a dynamical system.
, is then defined to be a dynamical system.The map
 embodies the time evolution of the dynamical system. Thus, for discrete dynamical systems the iterates
embodies the time evolution of the dynamical system. Thus, for discrete dynamical systems the iteratesIterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
 for integer n are studied. For continuous dynamical systems, the map
for integer n are studied. For continuous dynamical systems, the map  is understood to be a finite time evolution map and the construction is more complicated.
is understood to be a finite time evolution map and the construction is more complicated.Internal links
- Arnold's cat mapArnold's cat mapIn mathematics, Arnold's cat map is a chaotic map from the torus into itself, named after Vladimir Arnold, who demonstrated its effects in the 1960s using an image of a cat, hence the name....
- Baker's mapBaker's mapIn dynamical systems theory, the baker's map is a chaotic map from the unit square into itself. It is named after a kneading operation that bakers apply to dough: the dough is cut in half, and the two halves are stacked on one-another, and compressed...
is an example of a chaotic piecewise linear map - Circle mapCircle mapIn mathematics, a circle map is a member of a family of dynamical systems on the circle first defined by Andrey Kolmogorov. Kolmogorov proposed this family as a simplified model for driven mechanical rotors . The circle map equations also describe a simplified model of the phase-locked loop in...
- Double pendulumDouble pendulumIn mathematics, in the area of dynamical systems, a double pendulum is a pendulum with another pendulum attached to its end, and is a simple physical system that exhibits rich dynamic behavior with a strong sensitivity to initial conditions. The motion of a double pendulum is governed by a set of...
- BilliardsDynamical billiardsA billiard is a dynamical system in which a particle alternates between motion in a straight line and specular reflections from a boundary. When the particle hits the boundary it reflects from it without loss of speed...
and Outer BilliardsDynamical outer billiardsOuter Billiards is a dynamical system based on a convex shape in the plane.Classically, this system is defined for the Euclidean plane but one canalso consider the system in the hyperbolic plane or in other spaces thatsuitably generalize the plane.... - Hénon map
- Horseshoe mapHorseshoe mapIn the mathematics of chaos theory, a horseshoe map is any member of a class of chaotic maps of the square into itself. It is a core example in the study of dynamical systems. The map was introduced by Stephen Smale while studying the behavior of the orbits of the van der Pol oscillator...
- Irrational rotationIrrational rotationIn mathematical theory of dynamical systems, an irrational rotation is a mapwhere θ is an irrational number. Under the identification of a circle with R/Z, or with the interval [0, 1] with the boundary points glued together, this map becomes a rotation of a circle by a proportion θ of a full...
- List of chaotic maps
- Logistic mapLogistic mapThe logistic map is a polynomial mapping of degree 2, often cited as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations...
- Lorenz systemLorenz attractorThe Lorenz attractor, named for Edward N. Lorenz, is an example of a non-linear dynamic system corresponding to the long-term behavior of the Lorenz oscillator. The Lorenz oscillator is a 3-dimensional dynamical system that exhibits chaotic flow, noted for its lemniscate shape...
- Rossler map
External links
Multidimensional generalization
Dynamical systems are defined over a single independent variable, usually thought of as time. A more general class of systems are defined over multiple independent variables and are therefore called multidimensional systemsMultidimensional systems
By the term multidimensional systems or m-D systems we mean the branch of systems theory where not only one variable exists , but several independent variables....
. Such systems are useful for modeling, for example, image processing
Image processing
In electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
.
See also
- Behavioral modelingBehavioral modelingIn behavioral science, system theory and dynamic systems modeling, a behavioral model reproduces the required behavior of the original analyzed system, such as there is a one-to-one correspondence between the behavior of the original system and the simulated system. That namely implies that the...
- Dynamical systems theoryDynamical systems theoryDynamical systems theory is an area of applied mathematics used to describe the behavior of complex dynamical systems, usually by employing differential equations or difference equations. When differential equations are employed, the theory is called continuous dynamical systems. When difference...
- Feedback passivationFeedback passivationIn nonlinear control, feedback passivation is the use of feedback to convert a nonpassive dynamical system into a passive one....
- List of dynamical system topics
- OscillationOscillationOscillation is the repetitive variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples include a swinging pendulum and AC power. The term vibration is sometimes used more narrowly to mean a mechanical oscillation but sometimes...
- People in systems and controlPeople in systems and controlThis is an alphabetical list of people who have made significant contributions in the fields of system analysis and control theory.-Active researchers:-Historical figures in systems and control:...
- Sarkovskii's theoremSarkovskii's theoremIn mathematics, Sharkovskii's theorem, named after Oleksandr Mikolaiovich Sharkovsky, is a result about discrete dynamical systems. One of the implications of the theorem is that if a continuous discrete dynamical system on the real line has a periodic point of period 3, then it must have...
- System dynamicsSystem dynamicsSystem dynamics is an approach to understanding the behaviour of complex systems over time. It deals with internal feedback loops and time delays that affect the behaviour of the entire system. What makes using system dynamics different from other approaches to studying complex systems is the use...
- Systems theorySystems theorySystems theory is the transdisciplinary study of systems in general, with the goal of elucidating principles that can be applied to all types of systems at all nesting levels in all fields of research...
Further reading
Works providing a broad coverage: (available as a reprint: ISBN 0-201-40840-6)- Encyclopaedia of Mathematical Sciences (ISSN 0938-0396) has a sub-series on dynamical systems with reviews of current research.
Introductory texts with a unique perspective:
Textbooks
Popularizations:
External links
- A collection of dynamic and non-linear system models and demo applets (in Monash University's Virtual Lab)
- Arxiv preprint server has daily submissions of (non-refereed) manuscripts in dynamical systems.
- DSWeb provides up-to-date information on dynamical systems and its applications.
- Encyclopedia of dynamical systems A part of ScholarpediaScholarpediaScholarpedia is an English-language online wiki-based encyclopedia that uses the same MediaWiki software as Wikipedia, but has features more commonly associated with open-access online academic journals....
— peer reviewed and written by invited experts. - Nonlinear Dynamics. Models of bifurcation and chaos by Elmer G. Wiens
- Oliver Knill has a series of examples of dynamical systems with explanations and interactive controls.
- Sci.Nonlinear FAQ 2.0 (Sept 2003) provides definitions, explanations and resources related to nonlinear science
Online books or lecture notes:
- Geometrical theory of dynamical systems. Nils Berglund's lecture notes for a course at ETHEthEth is a letter used in Old English, Icelandic, Faroese , and Elfdalian. It was also used in Scandinavia during the Middle Ages, but was subsequently replaced with dh and later d. The capital eth resembles a D with a line through the vertical stroke...
at the advanced undergraduate level. - Dynamical systems. George D. Birkhoff's 1927 book already takes a modern approach to dynamical systems.
- Chaos: classical and quantum. An introduction to dynamical systems from the periodic orbit point of view.
- Modeling Dynamic Systems. An introduction to the development of mathematical models of dynamic systems.
- Learning Dynamical Systems. Tutorial on learning dynamical systems.
- Ordinary Differential Equations and Dynamical Systems. Lecture notes by Gerald TeschlGerald TeschlGerald Teschl is an Austrian mathematical physicist and Professor of Mathematics.He is working in the area of mathematical physics; in particular direct and inverse spectral theory with application to completely integrable partial differential equations .-Career:After studying physics at the Graz...
Research groups:
- Dynamical Systems Group Groningen, IWI, University of Groningen.
- Chaos @ UMD. Concentrates on the applications of dynamical systems.
- Dynamical Systems, SUNY Stony Brook. Lists of conferences, researchers, and some open problems.
- Center for Dynamics and Geometry, Penn State.
- Control and Dynamical Systems, Caltech.
- Laboratory of Nonlinear Systems, Ecole Polytechnique Fédérale de Lausanne (EPFL).
- Center for Dynamical Systems, University of Bremen
- Systems Analysis, Modelling and Prediction Group, University of Oxford
- Non-Linear Dynamics Group, Instituto Superior Técnico, Technical University of Lisbon
- Dynamical Systems, IMPA, Instituto Nacional de Matemática Pura e Applicada.
- Nonlinear Dynamics Workgroup, Institute of Computer Science, Czech Academy of Sciences.
Simulation software based on Dynamical Systems approach:










