
Maxwell's equations
Encyclopedia
Maxwell's equations are a set of partial differential equation
s that, together with the Lorentz force
law, form the foundation of classical electrodynamics, classical optics
, and electric circuits. These fields in turn underlie modern electrical and communications technologies.
Maxwell's equations have two major variants. The "microscopic" set of Maxwell's equations uses total charge and total current including the difficult-to-calculate atomic level charges and currents in materials. The "macroscopic" set of Maxwell's equations defines two new auxiliary fields that can sidestep having to know these 'atomic' sized charges and currents.
Maxwell's equations are named after the Scottish physicist and mathematician James Clerk Maxwell
, since in an early form they are all found in a four-part paper, "On Physical Lines of Force
," which he published between 1861 and 1862. The mathematical form of the Lorentz force law also appeared in this paper.
It is often useful to write Maxwell's equations in other forms; these representations are still formally termed "Maxwell's equations". A relativistic formulation in terms of covariant field tensors is used in special relativity, while, in quantum mechanics, a version based on the electric
and magnetic potential
s is preferred.
s and electric current
s act as sources for the electric and magnetic fields. Further, it describes how a time varying electric field generates a time varying magnetic field and vice versa. (See below for a mathematical description of these laws.) Of the four equations, two of them, Gauss's law
and Gauss's law for magnetism, describe how the fields emanate from charges. (For the magnetic field there is no magnetic charge and therefore magnetic fields lines neither begin nor end anywhere.) The other two equations describe how the fields 'circulate' around their respective sources; the magnetic field 'circulates' around electric currents and time varying electric field in Ampère's law with Maxwell's correction, while the electric field 'circulates' around time varying magnetic fields in Faraday's law
.
and the electric charge
s that cause it: The electric field points away from positive charges and towards negative charges. In the field line description, electric field lines begin only at positive electric charges and end only at negative electric charges. 'Counting' the number of field lines in a closed surface, therefore, yields the total charge enclosed by that surface. More technically, it relates the electric flux through any hypothetical closed "Gaussian surface
" to the enclosed electric charge.
s), analogous to electric charges. Instead, the magnetic field due to materials is generated by a configuration called a dipole
. Magnetic dipoles are best represented as loops of current but resemble positive and negative 'magnetic charges', inseparably bound together, having no net 'magnetic charge'. In terms of field lines, this equation states that magnetic field lines neither begin nor end but make loops or extend to infinity and back. In other words, any magnetic field line that enters a given volume must somewhere exit that volume. Equivalent technical statements are that the sum total magnetic flux
through any Gaussian surface is zero, or that the magnetic field is a solenoidal vector field.
 Faraday's law describes how a time varying magnetic field
Faraday's law describes how a time varying magnetic field
creates ("induces") an electric field
. This aspect of electromagnetic induction
is the operating principle behind many electric generators: for example a rotating bar magnet creates a changing magnetic field, which in turn generates an electric field in a nearby wire. (Note: there are two closely related equations which are called Faraday's law. The form used in Maxwell's equations is always valid but more restrictive than that originally formulated by Michael Faraday
.)
 Ampère's law with Maxwell's correction states that magnetic fields can be generated in two ways: by electrical current (this was the original "Ampère's law") and by changing electric fields (this was "Maxwell's correction").
Ampère's law with Maxwell's correction states that magnetic fields can be generated in two ways: by electrical current (this was the original "Ampère's law") and by changing electric fields (this was "Maxwell's correction").
Maxwell's correction to Ampère's law is particularly important: it shows that not only a changing magnetic field induces an electric field, but also a changing electric field induces a magnetic field. Therefore, these equations allow self-sustaining "electromagnetic waves" to travel through empty space (see electromagnetic wave equation
).
The speed calculated for electromagnetic waves, which could be predicted from experiments on charges and currents,The quantity we would now call , with units of velocity, was directly measured before Maxwell's equations, in an 1855 experiment by Wilhelm Eduard Weber
, with units of velocity, was directly measured before Maxwell's equations, in an 1855 experiment by Wilhelm Eduard Weber
and Rudolf Kohlrausch
. They charged a leyden jar
(a kind of capacitor
), and measured the electrostatic force
associated with the potential; then, they discharged it while measuring the magnetic force
from the current in the discharge-wire. Their result was , remarkably close to the speed of light. See The story of electrical and magnetic measurements: from 500 B.C. to the 1940s, by Joseph F. Keithley, p115 exactly matches the speed of light
; indeed, light
is one form of electromagnetic radiation
(as are X-ray
s, radio wave
s, and others). Maxwell understood the connection between electromagnetic waves and light in 1861, thereby unifying the theories of electromagnetism
and optics
.
(based on the cgs system), Lorentz–Heaviside units (used mainly in particle physics) and Planck units
(used in theoretical physics). See below for CGS-Gaussian units
.
For a description of the difference between the microscopic and macroscopic variants of Maxwell's equations see the relevant sections below.
In the equations given below, symbols in bold represent vector quantities, and symbols in italics represent scalar
quantities. The definitions of terms used in the two tables of equations are given in another table immediately following.
Here, in agreement with the common definition, it is assumed that one works in a system where the integration regions are constant. Thus, for example, However, exactly this equation, and not
However, exactly this equation, and not  would also be true, if S were to depend on time as well.
would also be true, if S were to depend on time as well.
unit of measure:






where P and M are polarization
and magnetization
, and ρb and Jb are bound charge and current, respectively. Substituting these equations into the 'macroscopic' Maxwell's equations gives identically the microscopic equations.
in the case of Gauss's law and Gauss's law for magnetism, and by the Kelvin–Stokes theorem in the case of Faraday's law and Ampère's law. Both the differential and integral forms are useful. The integral forms can often be used to simply and directly calculate fields from symmetric distributions of charges and currents. On the other hand, the differential forms are a more natural starting point for calculating the fields in more complicated (less symmetric) situations, for example using finite element analysis.




These equations lead directly to E and B satisfying the wave equation
for which the solutions are linear combinations of plane wave
s traveling at the speed of light
,

In addition, E and B are mutually perpendicular to each other and the direction of motion and are in phase with each other. A sinusoidal plane wave is one special solution of these equations.
In fact, Maxwell's equations explain how these waves can physically propagate through space. The changing magnetic field creates a changing electric field through Faraday's law
. In turn, that electric field creates a changing magnetic field through Maxwell's correction to Ampère's law. This perpetual cycle allows these waves, now known as electromagnetic radiation
, to move through space at velocity c.
P of the material, and the magnetic-H field, which is defined in terms of the magnetic-B field and the magnetization
M of the material.
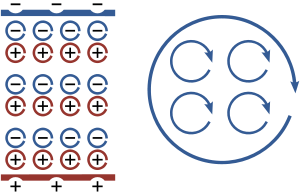 When an electric field is applied to a dielectric material
When an electric field is applied to a dielectric material
its molecules respond by forming microscopic electric dipoles—their atomic nuclei
move a tiny distance in the direction of the field, while their electron
s move a tiny distance in the opposite direction. This produces a macroscopic bound charge in the material even though all of the charges involved are bound to individual molecules. For example, if every molecule responds the same, similar to that shown in the figure, these tiny movements of charge combine to produce a layer of positive bound charge on one side of the material and a layer of negative charge on the other side. The bound charge is most conveniently described in terms of a polarization
, P, in the material. If P is uniform, a macroscopic separation of charge is produced only at the surfaces where P enter and leave the material. For non-uniform P, a charge is also produced in the bulk.
Somewhat similarly, in all materials the constituent atoms exhibit magnetic moments that are intrinsically linked to the angular momentum of the atoms' components, most notably their electrons. The connection to angular momentum suggests the picture of an assembly of microscopic current loops. Outside the material, an assembly of such microscopic current loops is not different from a macroscopic current circulating around the material's surface, despite the fact that no individual magnetic moment is traveling a large distance. These bound currents can be described using the magnetization
M.
The very complicated and granular bound charges and bound currents, therefore can be represented on the macroscopic scale in terms of P and M which average these charges and currents on a sufficiently large scale so as not to see the granularity of individual atoms, but also sufficiently small that they vary with location in the material. As such, the Maxwell's macroscopic equations ignores many details on a fine scale that may be unimportant to understanding matters on a grosser scale by calculating fields that are averaged over some suitably sized volume.
.
Determining the constitutive relationship between the auxiliary fields D and H and the E and B fields starts with the definition of the auxiliary fields themselves:

where P is the polarization
field and M is the magnetization
field which are defined in terms of microscopic bound charges and bound current respectively. Before getting to how to calculate M and P it is useful to examine some special cases, though.

where ε0 and μ0 are two universal constants, called the permittivity
of free space
and permeability of free space, respectively. Substituting these back into Maxwell's macroscopic equations lead directly to Maxwell's microscopic equations, except that the currents and charges are replaced with free currents and free charges. This is expected since there are no bound charges nor currents.

where χe and χm are the electric
and magnetic
susceptibilities of a given material respectively. In terms of D and H the constitutive relations are:

where ε and μ are constants (which depend on the material), called the permittivity
and permeability
, respectively, of the material. These are related to the susceptibilities by:

Substituting in the constitutive relations above into Maxwell's equations in linear, dispersionless, time-invariant materials (differential form only) are:



These are formally identical to the general formulation in terms of E and B (given above), except that the permittivity
of free space
was replaced with the permittivity
of the material, the permeability of free space was replaced with the permeability
of the material, and only free charges and currents are included (instead of all charges and currents). Unless that material is homogeneous in space, ε and μ cannot be factored out of the derivative expressions on the left sides.
, transport theory
or other tools of condensed matter physics
). The detail employed may be macroscopic
or microscopic
, depending upon the level necessary to the problem under scrutiny.
In general, though the constitutive relations can usually still be written:
but ε and μ are not, in general, simple constants, but rather functions. Examples are:
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s that, together with the Lorentz force
Lorentz force
In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
law, form the foundation of classical electrodynamics, classical optics
Optics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
, and electric circuits. These fields in turn underlie modern electrical and communications technologies.
Maxwell's equations have two major variants. The "microscopic" set of Maxwell's equations uses total charge and total current including the difficult-to-calculate atomic level charges and currents in materials. The "macroscopic" set of Maxwell's equations defines two new auxiliary fields that can sidestep having to know these 'atomic' sized charges and currents.
Maxwell's equations are named after the Scottish physicist and mathematician James Clerk Maxwell
James Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
, since in an early form they are all found in a four-part paper, "On Physical Lines of Force
On Physical Lines of Force
On Physical Lines of Force is a famous four-part paper written by James Clerk Maxwell published between 1861 and 1862. In it, Maxwell derived the equations of electromagnetism in conjunction with a "sea" of "molecular vortices" which he used to model Faraday's lines of force...
," which he published between 1861 and 1862. The mathematical form of the Lorentz force law also appeared in this paper.
It is often useful to write Maxwell's equations in other forms; these representations are still formally termed "Maxwell's equations". A relativistic formulation in terms of covariant field tensors is used in special relativity, while, in quantum mechanics, a version based on the electric
Electric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
and magnetic potential
Magnetic potential
The term magnetic potential can be used for either of two quantities in classical electromagnetism: the magnetic vector potential, A, and the magnetic scalar potential, ψ...
s is preferred.
Conceptual description
Conceptually, Maxwell's equations describe how electric chargeElectric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
s and electric current
Electric current
Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire...
s act as sources for the electric and magnetic fields. Further, it describes how a time varying electric field generates a time varying magnetic field and vice versa. (See below for a mathematical description of these laws.) Of the four equations, two of them, Gauss's law
Gauss's law
In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:...
and Gauss's law for magnetism, describe how the fields emanate from charges. (For the magnetic field there is no magnetic charge and therefore magnetic fields lines neither begin nor end anywhere.) The other two equations describe how the fields 'circulate' around their respective sources; the magnetic field 'circulates' around electric currents and time varying electric field in Ampère's law with Maxwell's correction, while the electric field 'circulates' around time varying magnetic fields in Faraday's law
Faraday's law of induction
Faraday's law of induction dates from the 1830s, and is a basic law of electromagnetism relating to the operating principles of transformers, inductors, and many types of electrical motors and generators...
.
Gauss's law
Gauss's law describes the relationship between an electric fieldElectric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
and the electric charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
s that cause it: The electric field points away from positive charges and towards negative charges. In the field line description, electric field lines begin only at positive electric charges and end only at negative electric charges. 'Counting' the number of field lines in a closed surface, therefore, yields the total charge enclosed by that surface. More technically, it relates the electric flux through any hypothetical closed "Gaussian surface
Gaussian surface
A Gaussian surface is a closed surface in three dimensional space through which the flux of an electromagnetic field is calculated. It is an arbitrary closed surface S=\partial V used in conjunction with Gauss's law in order to calculate the total enclosed electric charge by performing a surface...
" to the enclosed electric charge.
Gauss's law for magnetism
Gauss's law for magnetism states that there are no "magnetic charges" (also called magnetic monopoleMagnetic monopole
A magnetic monopole is a hypothetical particle in particle physics that is a magnet with only one magnetic pole . In more technical terms, a magnetic monopole would have a net "magnetic charge". Modern interest in the concept stems from particle theories, notably the grand unified and superstring...
s), analogous to electric charges. Instead, the magnetic field due to materials is generated by a configuration called a dipole
Dipole
In physics, there are several kinds of dipoles:*An electric dipole is a separation of positive and negative charges. The simplest example of this is a pair of electric charges of equal magnitude but opposite sign, separated by some distance. A permanent electric dipole is called an electret.*A...
. Magnetic dipoles are best represented as loops of current but resemble positive and negative 'magnetic charges', inseparably bound together, having no net 'magnetic charge'. In terms of field lines, this equation states that magnetic field lines neither begin nor end but make loops or extend to infinity and back. In other words, any magnetic field line that enters a given volume must somewhere exit that volume. Equivalent technical statements are that the sum total magnetic flux
Magnetic flux
Magnetic flux , is a measure of the amount of magnetic B field passing through a given surface . The SI unit of magnetic flux is the weber...
through any Gaussian surface is zero, or that the magnetic field is a solenoidal vector field.
Faraday's law

Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
creates ("induces") an electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
. This aspect of electromagnetic induction
Electromagnetic induction
Electromagnetic induction is the production of an electric current across a conductor moving through a magnetic field. It underlies the operation of generators, transformers, induction motors, electric motors, synchronous motors, and solenoids....
is the operating principle behind many electric generators: for example a rotating bar magnet creates a changing magnetic field, which in turn generates an electric field in a nearby wire. (Note: there are two closely related equations which are called Faraday's law. The form used in Maxwell's equations is always valid but more restrictive than that originally formulated by Michael Faraday
Michael Faraday
Michael Faraday, FRS was an English chemist and physicist who contributed to the fields of electromagnetism and electrochemistry....
.)
Ampère's law with Maxwell's correction

Maxwell's correction to Ampère's law is particularly important: it shows that not only a changing magnetic field induces an electric field, but also a changing electric field induces a magnetic field. Therefore, these equations allow self-sustaining "electromagnetic waves" to travel through empty space (see electromagnetic wave equation
Electromagnetic wave equation
The electromagnetic wave equation is a second-order partial differential equation that describes the propagation of electromagnetic waves through a medium or in a vacuum...
).
The speed calculated for electromagnetic waves, which could be predicted from experiments on charges and currents,The quantity we would now call
 , with units of velocity, was directly measured before Maxwell's equations, in an 1855 experiment by Wilhelm Eduard Weber
, with units of velocity, was directly measured before Maxwell's equations, in an 1855 experiment by Wilhelm Eduard WeberWilhelm Eduard Weber
Wilhelm Eduard Weber was a German physicist and, together with Carl Friedrich Gauss, inventor of the first electromagnetic telegraph.-Early years:...
and Rudolf Kohlrausch
Rudolf Kohlrausch
Rudolf Hermann Arndt Kohlrausch was a German physicist.-Biography:He was a native of Göttingen, the son of educator Heinrich Friedrich Theodor Kohlrausch...
. They charged a leyden jar
Leyden jar
A Leyden jar, or Leiden jar, is a device that "stores" static electricity between two electrodes on the inside and outside of a jar. It was invented independently by German cleric Ewald Georg von Kleist on 11 October 1745 and by Dutch scientist Pieter van Musschenbroek of Leiden in 1745–1746. The...
(a kind of capacitor
Capacitor
A capacitor is a passive two-terminal electrical component used to store energy in an electric field. The forms of practical capacitors vary widely, but all contain at least two electrical conductors separated by a dielectric ; for example, one common construction consists of metal foils separated...
), and measured the electrostatic force
Coulomb's law
Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
associated with the potential; then, they discharged it while measuring the magnetic force
Ampère's force law
In magnetostatics, the force of attraction or repulsion between two current-carrying wires is often called Ampère's force law...
from the current in the discharge-wire. Their result was , remarkably close to the speed of light. See The story of electrical and magnetic measurements: from 500 B.C. to the 1940s, by Joseph F. Keithley, p115 exactly matches the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
; indeed, light
Light
Light or visible light is electromagnetic radiation that is visible to the human eye, and is responsible for the sense of sight. Visible light has wavelength in a range from about 380 nanometres to about 740 nm, with a frequency range of about 405 THz to 790 THz...
is one form of electromagnetic radiation
Electromagnetic radiation
Electromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
(as are X-ray
X-ray
X-radiation is a form of electromagnetic radiation. X-rays have a wavelength in the range of 0.01 to 10 nanometers, corresponding to frequencies in the range 30 petahertz to 30 exahertz and energies in the range 120 eV to 120 keV. They are shorter in wavelength than UV rays and longer than gamma...
s, radio wave
Radio Wave
Radio Wave may refer to:*Radio frequency*Radio Wave 96.5, a radio station in Blackpool, UK...
s, and others). Maxwell understood the connection between electromagnetic waves and light in 1861, thereby unifying the theories of electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
and optics
Optics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
.
Units and summary of equations
Maxwell's equations vary with the unit system used. Though the general form remains the same, various definitions get changed and different constants appear at different places. (This may seem strange at first, but this is because some unit systems, e.g. variants of cgs, define their units in such a way that certain physical constants are fixed, dimensionless constants, e.g. 1, so these constants disappear from the equations.) The equations in this section are given in SI units. Other units commonly used are Gaussian unitsGaussian units
Gaussian units comprise a metric system of physical units. This system is the most common of the several electromagnetic unit systems based on cgs units. It is also called the Gaussian unit system, Gaussian-cgs units, or often just cgs units...
(based on the cgs system), Lorentz–Heaviside units (used mainly in particle physics) and Planck units
Planck units
In physics, Planck units are physical units of measurement defined exclusively in terms of five universal physical constants listed below, in such a manner that these five physical constants take on the numerical value of 1 when expressed in terms of these units. Planck units elegantly simplify...
(used in theoretical physics). See below for CGS-Gaussian units
Gaussian units
Gaussian units comprise a metric system of physical units. This system is the most common of the several electromagnetic unit systems based on cgs units. It is also called the Gaussian unit system, Gaussian-cgs units, or often just cgs units...
.
For a description of the difference between the microscopic and macroscopic variants of Maxwell's equations see the relevant sections below.
In the equations given below, symbols in bold represent vector quantities, and symbols in italics represent scalar
Scalar (physics)
In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations , or by Lorentz transformations or space-time translations . This is in contrast to a vector...
quantities. The definitions of terms used in the two tables of equations are given in another table immediately following.
Table of 'microscopic' equations
| Name | Differential form Partial differential equation In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables... |
Integral form Integral Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus... |
|---|---|---|
| Gauss's law |  |
 |
| Gauss's law for magnetism |  |
 |
| Maxwell–Faraday equation (Faraday's law of induction) |
 |
 |
| Ampère's circuital law (with Maxwell's correction) |
 |
 |
Here, in agreement with the common definition, it is assumed that one works in a system where the integration regions are constant. Thus, for example,
 However, exactly this equation, and not
However, exactly this equation, and not  would also be true, if S were to depend on time as well.
would also be true, if S were to depend on time as well.Table of 'macroscopic' equations
| Name | Differential form | Integral form |
|---|---|---|
| Gauss's law Gauss's law In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:... |
 |
 |
| Gauss's law for magnetism |  |
 |
| Maxwell–Faraday equation (Faraday's law of induction Faraday's law of induction Faraday's law of induction dates from the 1830s, and is a basic law of electromagnetism relating to the operating principles of transformers, inductors, and many types of electrical motors and generators... ) |
 |
 |
| Ampère's circuital law (with Maxwell's correction) |
 |
 |
Table of terms used in Maxwell's equations
The following table provides the meaning of each symbol and the SIInternational System of Units
The International System of Units is the modern form of the metric system and is generally a system of units of measurement devised around seven base units and the convenience of the number ten. The older metric system included several groups of units...
unit of measure:
| Symbol | Meaning (first term is the most common) | SI Unit of Measure |
|---|---|---|
 |
electric field Electric field In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding... also called the electric field intensity |
volt Volt The volt is the SI derived unit for electric potential, electric potential difference, and electromotive force. The volt is named in honor of the Italian physicist Alessandro Volta , who invented the voltaic pile, possibly the first chemical battery.- Definition :A single volt is defined as the... per meter or, equivalently, newton per coulomb |
 |
magnetic field Magnetic field A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;... also called the magnetic induction also called the magnetic field density also called the magnetic flux density |
tesla Tesla (unit) The tesla is the SI derived unit of magnetic field B . One tesla is equal to one weber per square meter, and it was defined in 1960 in honour of the inventor, physicist, and electrical engineer Nikola Tesla... , or equivalently, weber Weber (unit) In physics, the weber is the SI unit of magnetic flux. A flux density of one Wb/m2 is one tesla.The weber is named for the German physicist Wilhelm Eduard Weber .- Definition :... per square meter, volt Volt The volt is the SI derived unit for electric potential, electric potential difference, and electromotive force. The volt is named in honor of the Italian physicist Alessandro Volta , who invented the voltaic pile, possibly the first chemical battery.- Definition :A single volt is defined as the... -second per square meter |
 |
electric displacement field also called the electric induction also called the electric flux density |
coulombs per square meter or equivalently, newton per volt Volt The volt is the SI derived unit for electric potential, electric potential difference, and electromotive force. The volt is named in honor of the Italian physicist Alessandro Volta , who invented the voltaic pile, possibly the first chemical battery.- Definition :A single volt is defined as the... -meter |
 |
magnetizing field also called auxiliary magnetic field also called magnetic field intensity also called magnetic field |
ampere Ampere The ampere , often shortened to amp, is the SI unit of electric current and is one of the seven SI base units. It is named after André-Marie Ampère , French mathematician and physicist, considered the father of electrodynamics... per meter |
 |
the divergence Divergence In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around... operator |
per meter (factor contributed by applying either operator) |
 |
the curl operator | |
 |
partial derivative Partial derivative In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant... with respect to time |
per second (factor contributed by applying the operator) |
 and and  |
 is any surface, and is any surface, and  is its boundary curve. The surface is fixed (unchanging in time). is its boundary curve. The surface is fixed (unchanging in time). |
|
 and and  |
 is any three-dimensional volume, and is any three-dimensional volume, and  is its boundary surface. The volume is fixed (unchanging in time). is its boundary surface. The volume is fixed (unchanging in time). |
|
 |
differential vector element of surface area A, with infinitesimal Infinitesimal Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an... ly small magnitude and direction normal Surface normal A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a... to surface S |
square meters |
 |
differential vector element of path length tangential to the path/curve | meters |
 |
permittivity of free space, also called the electric constant Electric constant The physical constant ε0, commonly called the vacuum permittivity, permittivity of free space or electric constant is an ideal, physical constant, which is the value of the absolute dielectric permittivity of classical vacuum... , a universal constant |
farads per meter |
 |
permeability of free space, also called the magnetic constant, a universal constant | henries per meter, or newtons per ampere squared |
 |
free charge density Charge density The linear, surface, or volume charge density is the amount of electric charge in a line, surface, or volume, respectively. It is measured in coulombs per meter , square meter , or cubic meter , respectively, and represented by the lowercase Greek letter Rho . Since there are positive as well as... (not including bound charge) |
coulombs per cubic meter |
 |
total charge density Charge density The linear, surface, or volume charge density is the amount of electric charge in a line, surface, or volume, respectively. It is measured in coulombs per meter , square meter , or cubic meter , respectively, and represented by the lowercase Greek letter Rho . Since there are positive as well as... (including both free and bound charge) |
coulombs per cubic meter |
 |
free current density Current density Current density is a measure of the density of flow of a conserved charge. Usually the charge is the electric charge, in which case the associated current density is the electric current per unit area of cross section, but the term current density can also be applied to other conserved... (not including bound current) |
amperes per square meter |
 |
total current density Current density Current density is a measure of the density of flow of a conserved charge. Usually the charge is the electric charge, in which case the associated current density is the electric current per unit area of cross section, but the term current density can also be applied to other conserved... (including both free and bound current) |
amperes per square meter |
 |
net free electric charge Electric charge Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two... within the three-dimensional volume V (not including bound charge) |
coulombs |
 |
net electric charge Electric charge Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two... within the three-dimensional volume V (including both free and bound charge) |
coulombs |
 |
line integral Line integral In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field... of the electric field along the boundary Boundary (topology) In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary... ∂S of a surface S (∂S is always a closed curve). |
joules per coulomb |
 |
line integral Line integral In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field... of the magnetic field over the closed boundary ∂S of the surface S |
tesla-meters |
 |
the electric flux (surface integral Surface integral In mathematics, a surface integral is a definite integral taken over a surface ; it can be thought of as the double integral analog of the line integral... of the electric field) through the (closed) surface  (the boundary of the volume V) (the boundary of the volume V) |
joule-meter per coulomb |
 |
the magnetic flux Magnetic flux Magnetic flux , is a measure of the amount of magnetic B field passing through a given surface . The SI unit of magnetic flux is the weber... (surface integral Surface integral In mathematics, a surface integral is a definite integral taken over a surface ; it can be thought of as the double integral analog of the line integral... of the magnetic B-field) through the (closed) surface  (the boundary of the volume V) (the boundary of the volume V) |
tesla meters-squared or webers |
 |
magnetic flux Magnetic flux Magnetic flux , is a measure of the amount of magnetic B field passing through a given surface . The SI unit of magnetic flux is the weber... through any surface S, not necessarily closed |
webers Weber (unit) In physics, the weber is the SI unit of magnetic flux. A flux density of one Wb/m2 is one tesla.The weber is named for the German physicist Wilhelm Eduard Weber .- Definition :... or equivalently, volt-seconds |
 |
electric flux through any surface S, not necessarily closed | joule-meters per coulomb |
 |
flux of electric displacement field through any surface S, not necessarily closed | coulombs |
 |
net free electrical current passing through the surface S (not including bound current) | amperes |
 |
net electrical current passing through the surface S (including both free and bound current) | amperes |
Proof that the two general formulations are equivalent
The two alternate general formulations of Maxwell's equations given above are mathematically equivalent and related by the following relations:





where P and M are polarization
Polarization density
In classical electromagnetism, polarization density is the vector field that expresses the density of permanent or induced electric dipole moments in a dielectric material. When a dielectric is placed in an external electric field, its molecules gain electric dipole moment and the dielectric is...
and magnetization
Magnetization
In classical electromagnetism, magnetization or magnetic polarization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material...
, and ρb and Jb are bound charge and current, respectively. Substituting these equations into the 'macroscopic' Maxwell's equations gives identically the microscopic equations.
Relationship between differential and integral forms
The differential and integral forms of the equations are mathematically equivalent, by the divergence theoremDivergence theorem
In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
in the case of Gauss's law and Gauss's law for magnetism, and by the Kelvin–Stokes theorem in the case of Faraday's law and Ampère's law. Both the differential and integral forms are useful. The integral forms can often be used to simply and directly calculate fields from symmetric distributions of charges and currents. On the other hand, the differential forms are a more natural starting point for calculating the fields in more complicated (less symmetric) situations, for example using finite element analysis.
Maxwell's 'microscopic' equations
The microscopic variant of Maxwell's equation expresses the electric E field and the magnetic B field in terms of the total charge and total current present including the charges and currents at the atomic level. It is sometimes called the general form of Maxwell's equations or "Maxwell's equations in a vacuum". Both variants of Maxwell's equations are equally general, though, as they are mathematically equivalent. The microscopic equations are most useful in waveguides for example, when there are no dielectric or magnetic materials nearby.| Name | Differential form | Integral form |
|---|---|---|
| Gauss's law |  |
 |
| Gauss's law for magnetism |  |
 |
| Maxwell–Faraday equation (Faraday's law of induction) |
 |
 |
| Ampère's circuital law (with Maxwell's correction) |
 |
 |
With neither charges nor currents
In a region with no charges (ρ 0) and no currents (J 0), such as in a vacuum, Maxwell's equations reduce to:



These equations lead directly to E and B satisfying the wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
for which the solutions are linear combinations of plane wave
Plane wave
In the physics of wave propagation, a plane wave is a constant-frequency wave whose wavefronts are infinite parallel planes of constant peak-to-peak amplitude normal to the phase velocity vector....
s traveling at the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
,

In addition, E and B are mutually perpendicular to each other and the direction of motion and are in phase with each other. A sinusoidal plane wave is one special solution of these equations.
In fact, Maxwell's equations explain how these waves can physically propagate through space. The changing magnetic field creates a changing electric field through Faraday's law
Faraday's law of induction
Faraday's law of induction dates from the 1830s, and is a basic law of electromagnetism relating to the operating principles of transformers, inductors, and many types of electrical motors and generators...
. In turn, that electric field creates a changing magnetic field through Maxwell's correction to Ampère's law. This perpetual cycle allows these waves, now known as electromagnetic radiation
Electromagnetic radiation
Electromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
, to move through space at velocity c.
Maxwell's 'macroscopic' equations
Unlike the 'microscopic' equations, "Maxwell's macroscopic equations", also known as Maxwell's equations in matter, factor out the bound charge and current to obtain equations that depend only on the free charges and currents. These equations are more similar to those that Maxwell himself introduced. The cost of this factorization is that additional fields need to be defined: the displacement field D which is defined in terms of the electric field E and the polarizationPolarization density
In classical electromagnetism, polarization density is the vector field that expresses the density of permanent or induced electric dipole moments in a dielectric material. When a dielectric is placed in an external electric field, its molecules gain electric dipole moment and the dielectric is...
P of the material, and the magnetic-H field, which is defined in terms of the magnetic-B field and the magnetization
Magnetization
In classical electromagnetism, magnetization or magnetic polarization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material...
M of the material.
Bound charge and current

Dielectric
A dielectric is an electrical insulator that can be polarized by an applied electric field. When a dielectric is placed in an electric field, electric charges do not flow through the material, as in a conductor, but only slightly shift from their average equilibrium positions causing dielectric...
its molecules respond by forming microscopic electric dipoles—their atomic nuclei
Atomic nucleus
The nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...
move a tiny distance in the direction of the field, while their electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s move a tiny distance in the opposite direction. This produces a macroscopic bound charge in the material even though all of the charges involved are bound to individual molecules. For example, if every molecule responds the same, similar to that shown in the figure, these tiny movements of charge combine to produce a layer of positive bound charge on one side of the material and a layer of negative charge on the other side. The bound charge is most conveniently described in terms of a polarization
Polarization density
In classical electromagnetism, polarization density is the vector field that expresses the density of permanent or induced electric dipole moments in a dielectric material. When a dielectric is placed in an external electric field, its molecules gain electric dipole moment and the dielectric is...
, P, in the material. If P is uniform, a macroscopic separation of charge is produced only at the surfaces where P enter and leave the material. For non-uniform P, a charge is also produced in the bulk.
Somewhat similarly, in all materials the constituent atoms exhibit magnetic moments that are intrinsically linked to the angular momentum of the atoms' components, most notably their electrons. The connection to angular momentum suggests the picture of an assembly of microscopic current loops. Outside the material, an assembly of such microscopic current loops is not different from a macroscopic current circulating around the material's surface, despite the fact that no individual magnetic moment is traveling a large distance. These bound currents can be described using the magnetization
Magnetization
In classical electromagnetism, magnetization or magnetic polarization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material...
M.
The very complicated and granular bound charges and bound currents, therefore can be represented on the macroscopic scale in terms of P and M which average these charges and currents on a sufficiently large scale so as not to see the granularity of individual atoms, but also sufficiently small that they vary with location in the material. As such, the Maxwell's macroscopic equations ignores many details on a fine scale that may be unimportant to understanding matters on a grosser scale by calculating fields that are averaged over some suitably sized volume.
Equations
| Name | Differential form Partial differential equation In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables... |
Integral form Integral Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus... |
|---|---|---|
| Gauss's law Gauss's law In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:... |
 |
 |
| Gauss's law for magnetism |  |
 |
| Maxwell–Faraday equation (Faraday's law of induction Faraday's law of induction Faraday's law of induction dates from the 1830s, and is a basic law of electromagnetism relating to the operating principles of transformers, inductors, and many types of electrical motors and generators... ) |
 |
 |
| Ampère's circuital law (with Maxwell's correction) |
 |
 |
Constitutive relations
In order to apply 'Maxwell's macroscopic equations', it is necessary to specify the relations between displacement field D and E, and the magnetic H-field H and B. These equations specify the response of bound charge and current to the applied fields and are called constitutive relationsConstitutive equation
In physics, a constitutive equation is a relation between two physical quantities that is specific to a material or substance, and approximates the response of that material to external forces...
.
Determining the constitutive relationship between the auxiliary fields D and H and the E and B fields starts with the definition of the auxiliary fields themselves:


where P is the polarization
Polarization density
In classical electromagnetism, polarization density is the vector field that expresses the density of permanent or induced electric dipole moments in a dielectric material. When a dielectric is placed in an external electric field, its molecules gain electric dipole moment and the dielectric is...
field and M is the magnetization
Magnetization
In classical electromagnetism, magnetization or magnetic polarization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material...
field which are defined in terms of microscopic bound charges and bound current respectively. Before getting to how to calculate M and P it is useful to examine some special cases, though.
Without magnetic or dielectric materials
In the absence of magnetic or dielectric materials, the constitutive relations are simple:
where ε0 and μ0 are two universal constants, called the permittivity
Electric constant
The physical constant ε0, commonly called the vacuum permittivity, permittivity of free space or electric constant is an ideal, physical constant, which is the value of the absolute dielectric permittivity of classical vacuum...
of free space
Vacuum
In everyday usage, vacuum is a volume of space that is essentially empty of matter, such that its gaseous pressure is much less than atmospheric pressure. The word comes from the Latin term for "empty". A perfect vacuum would be one with no particles in it at all, which is impossible to achieve in...
and permeability of free space, respectively. Substituting these back into Maxwell's macroscopic equations lead directly to Maxwell's microscopic equations, except that the currents and charges are replaced with free currents and free charges. This is expected since there are no bound charges nor currents.
Isotropic Linear materials
In an (isotropic) linear material, where P is proportional to E and M is proportional to B the constitutive relations are also straightforward. In terms of the polarization P and the magnetization M they are:
where χe and χm are the electric
Electric susceptibility
In electromagnetism, the electric susceptibility \chi_e is a dimensionless proportionality constant that indicates the degree of polarization of a dielectric material in response to an applied electric field...
and magnetic
Magnetic susceptibility
In electromagnetism, the magnetic susceptibility \chi_m is a dimensionless proportionality constant that indicates the degree of magnetization of a material in response to an applied magnetic field...
susceptibilities of a given material respectively. In terms of D and H the constitutive relations are:

where ε and μ are constants (which depend on the material), called the permittivity
Permittivity
In electromagnetism, absolute permittivity is the measure of the resistance that is encountered when forming an electric field in a medium. In other words, permittivity is a measure of how an electric field affects, and is affected by, a dielectric medium. The permittivity of a medium describes how...
and permeability
Permeability (electromagnetism)
In electromagnetism, permeability is the measure of the ability of a material to support the formation of a magnetic field within itself. In other words, it is the degree of magnetization that a material obtains in response to an applied magnetic field. Magnetic permeability is typically...
, respectively, of the material. These are related to the susceptibilities by:

Substituting in the constitutive relations above into Maxwell's equations in linear, dispersionless, time-invariant materials (differential form only) are:




These are formally identical to the general formulation in terms of E and B (given above), except that the permittivity
Electric constant
The physical constant ε0, commonly called the vacuum permittivity, permittivity of free space or electric constant is an ideal, physical constant, which is the value of the absolute dielectric permittivity of classical vacuum...
of free space
Vacuum
In everyday usage, vacuum is a volume of space that is essentially empty of matter, such that its gaseous pressure is much less than atmospheric pressure. The word comes from the Latin term for "empty". A perfect vacuum would be one with no particles in it at all, which is impossible to achieve in...
was replaced with the permittivity
Permittivity
In electromagnetism, absolute permittivity is the measure of the resistance that is encountered when forming an electric field in a medium. In other words, permittivity is a measure of how an electric field affects, and is affected by, a dielectric medium. The permittivity of a medium describes how...
of the material, the permeability of free space was replaced with the permeability
Permeability (electromagnetism)
In electromagnetism, permeability is the measure of the ability of a material to support the formation of a magnetic field within itself. In other words, it is the degree of magnetization that a material obtains in response to an applied magnetic field. Magnetic permeability is typically...
of the material, and only free charges and currents are included (instead of all charges and currents). Unless that material is homogeneous in space, ε and μ cannot be factored out of the derivative expressions on the left sides.
General case
For real-world materials, the constitutive relations are not linear, except approximately. Calculating the constitutive relations from first principles involves determining how P and M are created from a given E and B. These relations may be empirical (based directly upon measurements), or theoretical (based upon statistical mechanicsStatistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, transport theory
Transport phenomena (engineering & physics)
In engineering and physics, the study of transport phenomena concerns the exchange of mass, energy, or momentum between observed and studied engineering systems. This subject is a fundamental component of disciplines involved with fluid mechanics, heat transfer, and mass transfer...
or other tools of condensed matter physics
Condensed matter physics
Condensed matter physics deals with the physical properties of condensed phases of matter. These properties appear when a number of atoms at the supramolecular and macromolecular scale interact strongly and adhere to each other or are otherwise highly concentrated in a system. The most familiar...
). The detail employed may be macroscopic
Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
or microscopic
Green-Kubo relations
The Green–Kubo relations give the exact mathematical expression for transport coefficients in terms of integrals of time correlation functions.-Thermal and mechanical transport processes:...
, depending upon the level necessary to the problem under scrutiny.
In general, though the constitutive relations can usually still be written:

but ε and μ are not, in general, simple constants, but rather functions. Examples are:
- DispersionDispersion (optics)In optics, dispersion is the phenomenon in which the phase velocity of a wave depends on its frequency, or alternatively when the group velocity depends on the frequency.Media having such a property are termed dispersive media...
and absorptionAbsorption (electromagnetic radiation)In physics, absorption of electromagnetic radiation is the way by which the energy of a photon is taken up by matter, typically the electrons of an atom. Thus, the electromagnetic energy is transformed to other forms of energy for example, to heat. The absorption of light during wave propagation is...
where ε and μ are functions of frequency. (Causality does not permit materials to be nondispersive; see, for example, Kramers–Kronig relations). Neither do the fields need to be in phase which leads to ε and μ being complexComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
. This also leads to absorption. - Bi-(an)isotropy where H and D depend on both B and E:

- NonlinearityNonlinear opticsNonlinear optics is the branch of optics that describes the behavior of light in nonlinear media, that is, media in which the dielectric polarization P responds nonlinearly to the electric field E of the light...
where ε and μ are functions of E and B. - Anisotropy (such as birefringenceBirefringenceBirefringence, or double refraction, is the decomposition of a ray of light into two rays when it passes through certain anisotropic materials, such as crystals of calcite or boron nitride. The effect was first described by the Danish scientist Rasmus Bartholin in 1669, who saw it in calcite...
or dichroismDichroismDichroism has two related but distinct meanings in optics. A dichroic material is either one which causes visible light to be split up into distinct beams of different wavelengths , or one in which light rays having different polarizations are absorbed by different amounts.The original meaning of...
) which occurs when ε and μ are second-rank tensorTensorTensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
s,
- Dependence of P and M on E and B at other locations and times. This could be due to spatial inhomogeneity; for example in a domained structureMagnetic domainsA magnetic domain describes a region within a magnetic material which has uniform magnetization. This means that the individual magnetic moments of the atoms are aligned with one another and they point in the same direction...
, heterostructureHeterojunction bipolar transistorThe heterojunction bipolar transistor is a type of bipolar junction transistor which uses differing semiconductor materials for the emitter and base regions, creating a heterojunction. The HBT improves on the BJT in that it that can handle signals of very high frequencies, up to several hundred...
or a liquid crystalLiquid crystalLiquid crystals are a state of matter that have properties between those of a conventional liquid and those of a solid crystal. For instance, an LC may flow like a liquid, but its molecules may be oriented in a crystal-like way. There are many different types of LC phases, which can be...
, or most commonly in the situation where there are simply multiple materials occupying different regions of space). Or it could be due to a time varying medium or due to hysteresisHysteresisHysteresis is the dependence of a system not just on its current environment but also on its past. This dependence arises because the system can be in more than one internal state. To predict its future evolution, either its internal state or its history must be known. If a given input alternately...
. In such cases P and M can be calculated as:

- in which the permittivity and permeability functions are replaced by integrals over the more general electricElectric susceptibilityIn electromagnetism, the electric susceptibility \chi_e is a dimensionless proportionality constant that indicates the degree of polarization of a dielectric material in response to an applied electric field...
and magneticMagnetic susceptibilityIn electromagnetism, the magnetic susceptibility \chi_m is a dimensionless proportionality constant that indicates the degree of magnetization of a material in response to an applied magnetic field...
susceptibilities.
In practice, some materials properties have a negligible impact in particular circumstances, permitting neglect of small effects. For example: optical nonlinearities can be neglected for low field strengths; material dispersion is unimportant when frequency is limited to a narrow bandwidth; material absorption can be neglected for wavelengths for which a material is transparent; and metalMetalA metal , is an element, compound, or alloy that is a good conductor of both electricity and heat. Metals are usually malleable and shiny, that is they reflect most of incident light...
s with finite conductivity often are approximated at microwaveMicrowaveMicrowaves, a subset of radio waves, have wavelengths ranging from as long as one meter to as short as one millimeter, or equivalently, with frequencies between 300 MHz and 300 GHz. This broad definition includes both UHF and EHF , and various sources use different boundaries...
or longer wavelengths as perfect metalsPerfect conductorA perfect conductor is an electrical conductor with no resistivity. The concept is used to model systems in which the electrical resistance or resistivity is negligible compared to other effects. One such model is ideal magnetohydrodynamics, the study of perfectly conductive fluids...
with infinite conductivity (forming hard barriers with zero skin depth of field penetration).
It may be noted that man-made materials can be designed to have customized permittivity and permeability, such as metamaterialMetamaterialMetamaterials are artificial materials engineered to have properties that may not be found in nature. Metamaterials usually gain their properties from structure rather than composition, using small inhomogeneities to create effective macroscopic behavior....
s and photonic crystalPhotonic crystalPhotonic crystals are periodic optical nanostructures that are designed to affect the motion of photons in a similar way that periodicity of a semiconductor crystal affects the motion of electrons...
s.
Calculation of constitutive relations
In general, the constitutive equations are theoretically determined by calculating how a molecule responds to the local fields through the Lorentz forceLorentz forceIn physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
. Other forces may need to be modeled as well such as lattice vibrations in crystals or bond forces. Including all of the forces leads to changes in the molecule which are used to calculate P and M as a function of the local fields.
The local fields differ from the applied fields due to the fields produced by the polarization and magnetization of nearby material; an effect which also needs to be modeled. Further, real materials are not continuous mediaContinuum mechanicsContinuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
; the local fields of real materials vary wildly on the atomic scale. The fields need to be averaged over a suitable volume to form a continuum approximation.
These continuum approximations often require some type of quantum mechanicalQuantum mechanicsQuantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
analysis such as quantum field theoryQuantum field theoryQuantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
as applied to condensed matter physicsCondensed matter physicsCondensed matter physics deals with the physical properties of condensed phases of matter. These properties appear when a number of atoms at the supramolecular and macromolecular scale interact strongly and adhere to each other or are otherwise highly concentrated in a system. The most familiar...
. See, for example, density functional theoryDensity functional theoryDensity functional theory is a quantum mechanical modelling method used in physics and chemistry to investigate the electronic structure of many-body systems, in particular atoms, molecules, and the condensed phases. With this theory, the properties of a many-electron system can be determined by...
, Green–Kubo relations and Green's functionGreen's function (many-body theory)In many-body theory, the term Green's function is sometimes used interchangeably with correlation function, but refers specifically to correlators of field operators or creation and annihilation operators....
. Various approximate transport equations have evolved, for example, the Boltzmann equationBoltzmann equationThe Boltzmann equation, also often known as the Boltzmann transport equation, devised by Ludwig Boltzmann, describes the statistical distribution of one particle in rarefied gas...
or the Fokker–Planck equation or the Navier–Stokes equations. Some examples where these equations are applied are magnetohydrodynamicsMagnetohydrodynamicsMagnetohydrodynamics is an academic discipline which studies the dynamics of electrically conducting fluids. Examples of such fluids include plasmas, liquid metals, and salt water or electrolytes...
, fluid dynamicsFluid dynamicsIn physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
, electrohydrodynamicsElectrohydrodynamicsElectrohydrodynamics , also known as electro-fluid-dynamics or electrokinetics, is the study of the dynamics of electrically charged fluids. It is the study of the motions of ionised particles or molecules and their interactions with electric fields and the surrounding fluid...
, superconductivitySuperconductivitySuperconductivity is a phenomenon of exactly zero electrical resistance occurring in certain materials below a characteristic temperature. It was discovered by Heike Kamerlingh Onnes on April 8, 1911 in Leiden. Like ferromagnetism and atomic spectral lines, superconductivity is a quantum...
, plasma modelingPlasma modelingPlasma Modeling refers to solving equations of motion that describe the state of a plasma. It is generally coupled with Maxwell's Equations for electromagnetic fields...
. An entire physical apparatus for dealing with these matters has developed. A different set of homogenization methods (evolving from a tradition in treating materials such as conglomeratesConglomerate (geology)A conglomerate is a rock consisting of individual clasts within a finer-grained matrix that have become cemented together. Conglomerates are sedimentary rocks consisting of rounded fragments and are thus differentiated from breccias, which consist of angular clasts...
and laminateLaminateA laminate is a material that can be constructed by uniting two or more layers of material together. The process of creating a laminate is lamination, which in common parlance refers to the placing of something between layers of plastic and gluing them with heat and/or pressure, usually with an...
s) are based upon approximation of an inhomogeneous material by a homogeneous effective mediumEffective Medium ApproximationsEffective medium approximations or effective medium theory are physical models that describe the macroscopic properties of a medium based on the properties and the relative fractions of its components...
(valid for excitations with wavelengthWavelengthIn physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
s much larger than the scale of the inhomogeneity).
The theoretical modeling of the continuum-approximation properties of many real materials often rely upon measurement as well, for example, ellipsometryEllipsometryEllipsometry is an optical technique for the investigation of the dielectric properties of thin films....
measurements.
Relation between electricity, magnetism, and the speed of light
The relation between electricity, magnetism, and the speed of light can be summarized by the modern equation:
The left-hand side is the speed of light, and the right-hand side is a quantity related to the equations governing electricity and magnetism. Although the right-hand side has units of velocity, it can be inferred from measurements of electric and magnetic forces, which involve no physical velocities. Therefore, establishing this relationship provided convincing evidence that light is an electromagnetic phenomenon.
The discovery of this relationship started in 1855, when Wilhelm Eduard WeberWilhelm Eduard WeberWilhelm Eduard Weber was a German physicist and, together with Carl Friedrich Gauss, inventor of the first electromagnetic telegraph.-Early years:...
and Rudolf KohlrauschRudolf KohlrauschRudolf Hermann Arndt Kohlrausch was a German physicist.-Biography:He was a native of Göttingen, the son of educator Heinrich Friedrich Theodor Kohlrausch...
determined that there was a quantity related to electricity and magnetism, "the ratio of the absolute electromagnetic unit of charge to the absolute electrostatic unit of charge" (in modern language, the value ), and determined that it should have units of velocity. They then measured this ratio by an experiment which involved charging and discharging a Leyden jarLeyden jarA Leyden jar, or Leiden jar, is a device that "stores" static electricity between two electrodes on the inside and outside of a jar. It was invented independently by German cleric Ewald Georg von Kleist on 11 October 1745 and by Dutch scientist Pieter van Musschenbroek of Leiden in 1745–1746. The...
), and determined that it should have units of velocity. They then measured this ratio by an experiment which involved charging and discharging a Leyden jarLeyden jarA Leyden jar, or Leiden jar, is a device that "stores" static electricity between two electrodes on the inside and outside of a jar. It was invented independently by German cleric Ewald Georg von Kleist on 11 October 1745 and by Dutch scientist Pieter van Musschenbroek of Leiden in 1745–1746. The...
and measuring the magnetic force from the discharge current, and found a value , remarkably close to the speed of light, which had recently been measured at by Hippolyte FizeauHippolyte FizeauArmand Hippolyte Louis Fizeau was a French physicist.-Biography:Fizeau was born in Paris. His earliest work was concerned with improvements in photographic processes. Following suggestions by François Arago, Léon Foucault and Fizeau collaborated in a series of investigations on the interference of...
in 1848 and at by Léon FoucaultLéon FoucaultJean Bernard Léon Foucault was a French physicist best known for the invention of the Foucault pendulum, a device demonstrating the effect of the Earth's rotation...
in 1850. However, Weber and Kohlrausch did not make the connection to the speed of light. Towards the end of 1861 while working on part III of his paper On Physical Lines of ForceOn Physical Lines of ForceOn Physical Lines of Force is a famous four-part paper written by James Clerk Maxwell published between 1861 and 1862. In it, Maxwell derived the equations of electromagnetism in conjunction with a "sea" of "molecular vortices" which he used to model Faraday's lines of force...
, Maxwell travelled from Scotland to London and looked up Weber and Kohlrausch's results. He converted them into a format which was compatible with his own writings, and in doing so he established the connection to the speed of light and concluded that light is a form of electromagnetic radiation.
The term Maxwell's equations
The four modern Maxwell's equations can be found individually throughout his 1861 paper, derived theoretically using a molecular vortex model of Michael FaradayMichael FaradayMichael Faraday, FRS was an English chemist and physicist who contributed to the fields of electromagnetism and electrochemistry....
's "lines of force" and in conjunction with the experimental result of Weber and Kohlrausch. But it wasn't until 1884 that Oliver HeavisideOliver HeavisideOliver Heaviside was a self-taught English electrical engineer, mathematician, and physicist who adapted complex numbers to the study of electrical circuits, invented mathematical techniques to the solution of differential equations , reformulated Maxwell's field equations in terms of electric and...
, concurrently with similar work by Willard Gibbs and Heinrich Hertz, grouped the four together into a distinct set. This group of four equations was known variously as the Hertz-Heaviside equations and the Maxwell-Hertz equations, and are sometimes still known as the Maxwell–Heaviside equations.
Maxwell's contribution to science in producing these equations lies in the correction he made to Ampère's circuital law in his 1861 paper On Physical Lines of ForceOn Physical Lines of ForceOn Physical Lines of Force is a famous four-part paper written by James Clerk Maxwell published between 1861 and 1862. In it, Maxwell derived the equations of electromagnetism in conjunction with a "sea" of "molecular vortices" which he used to model Faraday's lines of force...
. He added the displacement currentDisplacement currentIn electromagnetism, displacement current is a quantity that is defined in terms of the rate of change of electric displacement field. Displacement current has the units of electric current density, and it has an associated magnetic field just as actual currents do. However it is not an electric...
term to Ampère's circuital law and this enabled him to derive the electromagnetic wave equationElectromagnetic wave equationThe electromagnetic wave equation is a second-order partial differential equation that describes the propagation of electromagnetic waves through a medium or in a vacuum...
in his later 1865 paper A Dynamical Theory of the Electromagnetic FieldA Dynamical Theory of the Electromagnetic Field"A Dynamical Theory of the Electromagnetic Field" is the third of James Clerk Maxwell's papers regarding electromagnetism, published in 1865. It is the paper in which the original set of four Maxwell's equations first appeared...
and demonstrate the fact that light is an electromagnetic wave. This fact was then later confirmed experimentally by Heinrich Hertz in 1887. The physicist Richard FeynmanRichard FeynmanRichard Phillips Feynman was an American physicist known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics and the physics of the superfluidity of supercooled liquid helium, as well as in particle physics...
predicted that, "The American Civil War will pale into provincial insignificance in comparison with this important scientific event of the same decade."
The concept of fields was introduced by, among others, Faraday. Albert EinsteinAlbert EinsteinAlbert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
wrote:
Heaviside worked to eliminate the potentials (electric potentialElectric potentialIn classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
and magnetic potentialMagnetic potentialThe term magnetic potential can be used for either of two quantities in classical electromagnetism: the magnetic vector potential, A, and the magnetic scalar potential, ψ...
) that Maxwell had used as the central concepts in his equations; this effort was somewhat controversial, though it was understood by 1884 that the potentials must propagate at the speed of light like the fields, unlike the concept of instantaneous action-at-a-distance like the then conception of gravitational potential. Modern analysis of, for example, radio antennas, makes full use of Maxwell's vector and scalar potentials to separate the variables, a common technique used in formulating the solutions of differential equations. However, the potentials can be introduced by algebraic manipulation of the four fundamental equations.
On Physical Lines of Force
The four modern day Maxwell's equations appeared throughout Maxwell's 1861 paper On Physical Lines of Force:
- Equation (56) in Maxwell's 1861 paper is ∇ ⋅ B = 0.
- Equation (112) is Ampère's circuital law with Maxwell's displacement current added. It is the addition of displacement currentDisplacement currentIn electromagnetism, displacement current is a quantity that is defined in terms of the rate of change of electric displacement field. Displacement current has the units of electric current density, and it has an associated magnetic field just as actual currents do. However it is not an electric...
that is the most significant aspect of Maxwell's work in electromagnetismElectromagnetismElectromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
, as it enabled him to later derive the electromagnetic wave equationElectromagnetic wave equationThe electromagnetic wave equation is a second-order partial differential equation that describes the propagation of electromagnetic waves through a medium or in a vacuum...
in his 1865 paper A Dynamical Theory of the Electromagnetic FieldA Dynamical Theory of the Electromagnetic Field"A Dynamical Theory of the Electromagnetic Field" is the third of James Clerk Maxwell's papers regarding electromagnetism, published in 1865. It is the paper in which the original set of four Maxwell's equations first appeared...
, and hence show that light is an electromagnetic wave. It is therefore this aspect of Maxwell's work which gives the equations their full significance. (Interestingly, Kirchhoff derived the telegrapher's equations in 1857 without using displacement currentDisplacement currentIn electromagnetism, displacement current is a quantity that is defined in terms of the rate of change of electric displacement field. Displacement current has the units of electric current density, and it has an associated magnetic field just as actual currents do. However it is not an electric...
. But he did use Poisson's equation and the equation of continuity which are the mathematical ingredients of the displacement currentDisplacement currentIn electromagnetism, displacement current is a quantity that is defined in terms of the rate of change of electric displacement field. Displacement current has the units of electric current density, and it has an associated magnetic field just as actual currents do. However it is not an electric...
. Nevertheless, Kirchhoff believed his equations to be applicable only inside an electric wire and so he is not credited with having discovered that light is an electromagnetic wave). - Equation (115) is Gauss's lawGauss's lawIn physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:...
. - Equation (54) is an equation that Oliver HeavisideOliver HeavisideOliver Heaviside was a self-taught English electrical engineer, mathematician, and physicist who adapted complex numbers to the study of electrical circuits, invented mathematical techniques to the solution of differential equations , reformulated Maxwell's field equations in terms of electric and...
referred to as 'Faraday's law'. This equation caters for the time varying aspect of electromagnetic induction, but not for the motionally induced aspect, whereas Faraday's original flux law caters for both aspects. Maxwell deals with the motionally dependent aspect of electromagnetic induction, v × B, at equation (77). Equation (77) which is the same as equation (D) in the original eight Maxwell's equations listed below, corresponds to all intents and purposes to the modern day force law F = q( E + v × B ) which sits adjacent to Maxwell's equations and bears the name Lorentz forceLorentz forceIn physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
, even though Maxwell derived it when Lorentz was still a young boy.
The difference between the B and the H vectors can be traced back to Maxwell's 1855 paper entitled On Faraday's Lines of Force which was read to the Cambridge Philosophical SocietyCambridge Philosophical SocietyThe Cambridge Philosophical Society is a scientific society at University of Cambridge. It was founded in 1819. The name derives from the medieval use of the word philosophy to denote any research undertaken outside the fields of theology and medicine...
. The paper presented a simplified model of Faraday's work, and how the two phenomena were related. He reduced all of the current knowledge into a linked set of differential equationDifferential equationA differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s.
It is later clarified in his concept of a sea of molecular vortices that appears in his 1861 paper On Physical Lines of ForceOn Physical Lines of ForceOn Physical Lines of Force is a famous four-part paper written by James Clerk Maxwell published between 1861 and 1862. In it, Maxwell derived the equations of electromagnetism in conjunction with a "sea" of "molecular vortices" which he used to model Faraday's lines of force...
. Within that context, H represented pure vorticity (spin), whereas B was a weighted vorticity that was weighted for the density of the vortex sea. Maxwell considered magnetic permeability µ to be a measure of the density of the vortex sea. Hence the relationship,
- Magnetic induction current causes a magnetic current density
was essentially a rotational analogy to the linear electric current relationship,- Electric convection current
where ρ is electric charge density. B was seen as a kind of magnetic current of vortices aligned in their axial planes, with H being the circumferential velocity of the vortices. With µ representing vortex density, it follows that the product of µ with vorticity H leads to the magnetic fieldMagnetic fieldA magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
denoted as B.
The electric current equation can be viewed as a convective current of electric chargeElectric chargeElectric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
that involves linear motion. By analogy, the magnetic equation is an inductive current involving spin. There is no linear motion in the inductive current along the direction of the B vector. The magnetic inductive current represents lines of force. In particular, it represents lines of inverse square law force.
The extension of the above considerations confirms that where B is to H, and where J is to ρ, then it necessarily follows from Gauss's law and from the equation of continuity of charge that E is to D. i.e. B parallels with E, whereas H parallels with D.
A Dynamical Theory of the Electromagnetic Field
In 1864 Maxwell published A Dynamical Theory of the Electromagnetic FieldA Dynamical Theory of the Electromagnetic Field"A Dynamical Theory of the Electromagnetic Field" is the third of James Clerk Maxwell's papers regarding electromagnetism, published in 1865. It is the paper in which the original set of four Maxwell's equations first appeared...
in which he showed that light was an electromagnetic phenomenon.
Confusion over the term "Maxwell's equations" sometimes arises because it has been used for a set of eight equations that appeared in Part III of Maxwell's 1864 paper A Dynamical Theory of the Electromagnetic FieldA Dynamical Theory of the Electromagnetic Field"A Dynamical Theory of the Electromagnetic Field" is the third of James Clerk Maxwell's papers regarding electromagnetism, published in 1865. It is the paper in which the original set of four Maxwell's equations first appeared...
, entitled "General Equations of the Electromagnetic Field," and this confusion is compounded by the writing of six of those eight equations as three separate equations (one for each of the Cartesian axes), resulting in twenty equations and twenty unknowns. (As noted above, this terminology is not common: Modern references to the term "Maxwell's equations" refer to the Heaviside restatements.)
The eight original Maxwell's equations can be written in modern vector notation as follows:
(A) The law of total currents

(B) The equation of magnetic force

(C) Ampère's circuital law

(D) Electromotive force created by convection, induction, and by static electricity. (This is in effect the Lorentz forceLorentz forceIn physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
)

(E) The electric elasticity equation

(F) Ohm's law

(G) Gauss's law

(H) Equation of continuity

or

Notation- H is the magnetizing field, which Maxwell called the magnetic intensity.
- J is the current densityCurrent densityCurrent density is a measure of the density of flow of a conserved charge. Usually the charge is the electric charge, in which case the associated current density is the electric current per unit area of cross section, but the term current density can also be applied to other conserved...
(withJtot being the total current including displacement current).Here it is noted that a quite different quantity, the magnetic polarization, μ0M by decision of an international IUPAP commission has been given the same name J. So for the electric current density, a name with small letters, j would be better. But even then the mathematicians would still use the large-letter-name J for the corresponding current-twoform (see below). - D is the displacement field (called the electric displacement by Maxwell).
- ρ is the free charge density (called the quantity of free electricity by Maxwell).
- A is the magnetic potentialMagnetic potentialThe term magnetic potential can be used for either of two quantities in classical electromagnetism: the magnetic vector potential, A, and the magnetic scalar potential, ψ...
(called the angular impulse by Maxwell). - E is called the electromotive force by Maxwell. The term electromotive forceElectromotive forceIn physics, electromotive force, emf , or electromotance refers to voltage generated by a battery or by the magnetic force according to Faraday's Law, which states that a time varying magnetic field will induce an electric current.It is important to note that the electromotive "force" is not a...
is nowadays used for voltage, but it is clear from the context that Maxwell's meaning corresponded more to the modern term electric fieldElectric fieldIn physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
. - φ is the electric potentialElectric potentialIn classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
(which Maxwell also called electric potential). - σ is the electrical conductivity (Maxwell called the inverse of conductivity the specific resistance, what is now called the resistivityResistivityElectrical resistivity is a measure of how strongly a material opposes the flow of electric current. A low resistivity indicates a material that readily allows the movement of electric charge. The SI unit of electrical resistivity is the ohm metre...
).
It is interesting to note the μv × H term that appears in equation D. Equation D is therefore effectively the Lorentz forceLorentz forceIn physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
, similarly to equation (77) of his 1861 paper (see above).
When Maxwell derives the electromagnetic wave equationElectromagnetic wave equationThe electromagnetic wave equation is a second-order partial differential equation that describes the propagation of electromagnetic waves through a medium or in a vacuum...
in his 1865 paper, he uses equation D to cater for electromagnetic inductionElectromagnetic inductionElectromagnetic induction is the production of an electric current across a conductor moving through a magnetic field. It underlies the operation of generators, transformers, induction motors, electric motors, synchronous motors, and solenoids....
rather than Faraday's law of inductionFaraday's law of inductionFaraday's law of induction dates from the 1830s, and is a basic law of electromagnetism relating to the operating principles of transformers, inductors, and many types of electrical motors and generators...
which is used in modern textbooks. (Faraday's law itself does not appear among his equations.) However, Maxwell drops the μv × H term from equation D when he is deriving the electromagnetic wave equationElectromagnetic wave equationThe electromagnetic wave equation is a second-order partial differential equation that describes the propagation of electromagnetic waves through a medium or in a vacuum...
, as he considers the situation only from the rest frame.
A Treatise on Electricity and Magnetism
In A Treatise on Electricity and MagnetismA Treatise on Electricity and MagnetismA Treatise on Electricity and Magnetism is a two volume treatise on electromagnetism written by James Clerk Maxwell in 1873.-See also:* On Physical Lines of Force* A Dynamical Theory of the Electromagnetic Field-External links:...
, an 1873 treatiseTreatiseA treatise is a formal and systematic written discourse on some subject, generally longer and treating it in greater depth than an essay, and more concerned with investigating or exposing the principles of the subject.-Noteworthy treatises:...
on electromagnetismElectromagnetismElectromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
written by James Clerk MaxwellJames Clerk MaxwellJames Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
, eleven general equations of the electromagnetic field are listed and these include the eight that are listed in the 1865 paper.
Maxwell's equations and relativity
Maxwell's original equations are based on the idea that light travels through a sea of molecular vortices known as the 'luminiferous aetherLuminiferous aetherIn the late 19th century, luminiferous aether or ether, meaning light-bearing aether, was the term used to describe a medium for the propagation of light....
', and that the speed of light has to be respective to the reference frame of this aether. Measurements designed to measure the speed of the Earth through the aether conflicted, though.
A more theoretical approach was suggested by Hendrik LorentzHendrik LorentzHendrik Antoon Lorentz was a Dutch physicist who shared the 1902 Nobel Prize in Physics with Pieter Zeeman for the discovery and theoretical explanation of the Zeeman effect...
along with George FitzGeraldGeorge FitzGeraldGeorge Francis FitzGerald was an Irish professor of "natural and experimental philosophy" at Trinity College in Dublin, Ireland, during the last quarter of the 19th century....
and Joseph LarmorJoseph LarmorSir Joseph Larmor , a physicist and mathematician who made innovations in the understanding of electricity, dynamics, thermodynamics, and the electron theory of matter...
. Both Larmor (1897) and Lorentz (1899, 1904) derived the Lorentz transformationLorentz transformationIn physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
(so named by Henri PoincaréHenri PoincaréJules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
) as one under which Maxwell's equations were invariant. Poincaré (1900) analyzed the coordination of moving clocks by exchanging light signals. He also established mathematically the group property of the Lorentz transformation (Poincaré 1905).
EinsteinAlbert EinsteinAlbert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
dismissed the aether as unnecessary and concluded that Maxwell's equations predict the existence of a fixed speed of light, independent of the speed of the observer, and as such he used Maxwell's equations as the starting point for his special theory of relativity. In doing so, he established the Lorentz transformation as being valid for all matter and not just Maxwell's equations. Maxwell's equations played a key role in Einstein's famous paper on special relativity; for example, in the opening paragraph of the paper, he motivated his theory by noting that a description of a conductor moving with respect to a magnetMoving magnet and conductor problemThe moving magnet and conductor problem is a famous thought experiment, originating in the 19th century, concerning the intersection of classical electromagnetism and special relativity. In it, the current in a conductor moving with constant velocity, v, with respect to a magnet is calculated in...
must generate a consistent set of fields irrespective of whether the force is calculated in the rest frame of the magnet or that of the conductor.
General relativity has also had a close relationship with Maxwell's equations. For example, Theodor KaluzaTheodor KaluzaTheodor Franz Eduard Kaluza was a German mathematician and physicist known for the Kaluza-Klein theory involving field equations in five-dimensional space...
and Oskar KleinOskar KleinOskar Benjamin Klein was a Swedish theoretical physicist.Klein was born in Danderyd outside Stockholm, son of the chief rabbi of Stockholm, Dr. Gottlieb Klein from Homonna in Hungary and Antonie Levy...
showed in the 1920sKaluza–Klein theoryIn physics, Kaluza–Klein theory is a model that seeks to unify the two fundamental forces of gravitation and electromagnetism. The theory was first published in 1921. It was proposed by the mathematician Theodor Kaluza who extended general relativity to a five-dimensional spacetime...
that Maxwell's equations can be derived by extending general relativityGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
into five dimensions. This strategy of using higher dimensions to unify different forces remains an active area of research in particle physicsParticle physicsParticle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
.
Modified to include magnetic monopoles
Maxwell's equations provide for an electric charge, but posit no magnetic charge. Magnetic charge has never been seen and may not exist. Nevertheless, Maxwell's equations including magnetic charge (and magnetic current) is of some theoretical interest.
For one reason, Maxwell's equations can be made fully symmetric under interchange of electric and magnetic field by allowing for the possibility of magnetic charges with magnetic charge density ρm and currents with magnetic current density Jm. The extended Maxwell's equations (in cgs-Gaussian unitsGaussian unitsGaussian units comprise a metric system of physical units. This system is the most common of the several electromagnetic unit systems based on cgs units. It is also called the Gaussian unit system, Gaussian-cgs units, or often just cgs units...
) are:
Name Without magnetic monopoles With magnetic monopoles (hypothetical) Gauss's law Gauss's lawIn physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:...
:

Gauss's law for magnetism: 

Maxwell–Faraday equation
(Faraday's law of inductionFaraday's law of inductionFaraday's law of induction dates from the 1830s, and is a basic law of electromagnetism relating to the operating principles of transformers, inductors, and many types of electrical motors and generators...
):

Ampère's law Ampère's lawIn classical electromagnetism, Ampère's circuital law, discovered by André-Marie Ampère in 1826, relates the integrated magnetic field around a closed loop to the electric current passing through the loop...
(with Maxwell's extension):

If magnetic charges do not exist, or if they exist but not in the region studied, then the new variables are zero, and the symmetric equations reduce to the conventional equations of electromagnetism such as ∇ · B = 0. Further, if every particle has the same ratio of electric to magnetic charge, then an E and a B field can be defined that obeys the normal Maxwell's equation (having no magnetic charges or currents) with its own charge and current densities.
Solving Maxwell's equations
Maxwell's equations are partial differential equations that relate the electric and magnetic fields to each other and to the electric charges and currents. Often, the charges and currents are themselves dependent on the electric and magnetic fields via the Lorentz force equationLorentz forceIn physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
and the constitutive relations. These all form a set of coupled partial differential equations, which are often very difficult to solve. In fact, the solutions of these equations encompass all the diverse phenomena in the entire field of classical electromagnetismClassical electromagnetismClassical electromagnetism is a branch of theoretical physics that studies consequences of the electromagnetic forces between electric charges and currents...
. A thorough discussion is far beyond the scope of the article, but some general notes follow:- Like any differential equation, boundary conditions and initial conditions are necessary for a unique solution. For example, even with no charges and no currents anywhere in spacetime, many solutions to Maxwell's equations are possible, not just the obvious solution E=B=0. Another solution is E=constant, B=constant, while yet other solutions have electromagnetic waves filling spacetime. In some cases, Maxwell's equations are solved through infinite space, and boundary conditions are given as asymptotic limits at infinity. In other cases, Maxwell's equations are solved in just a finite region of space, with appropriate boundary conditions on that region: For example, the boundary could be a artificial absorbing boundaryPerfectly matched layerA perfectly matched layer is an artificial absorbing layer for wave equations, commonly used to truncate computational regions in numerical methods to simulate problems with open boundaries, especially in the FDTD and FEM methods...
representing the rest of the universe, or periodic boundary conditionsPeriodic boundary conditionsIn mathematical models and computer simulations, periodic boundary conditions are a set of boundary conditions that are often used to simulate a large system by modelling a small part that is far from its edge...
, or (as with a waveguideWaveguideA waveguide is a structure which guides waves, such as electromagnetic waves or sound waves. There are different types of waveguides for each type of wave...
or cavity resonatorResonatorA resonator is a device or system that exhibits resonance or resonant behavior, that is, it naturally oscillates at some frequencies, called its resonant frequencies, with greater amplitude than at others. The oscillations in a resonator can be either electromagnetic or mechanical...
) the boundary conditions may describe the walls that isolate a small region from the outside world. - Jefimenko's equationsJefimenko's equationsIn electromagnetism, Jefimenko's equations describe the behavior of the electric and magnetic fields in terms of the charge and current distributions at retarded times....
(or the closely related Liénard–Wiechert potentials) are the explicit solution to Maxwell's equations for the electric and magnetic fields created by any given distribution of charges and currents. It assumes specific initial conditions to obtain the so-called "retarded solution", where the only fields present are the ones created by the charges. Jefimenko's equations are not so helpful in situations when the charges and currents are themselves affected by the fields they create. - Numerical methods for differential equationsNumerical partial differential equationsNumerical partial differential equations is the branch of numerical analysis that studies the numerical solution of partial differential equations .Numerical techniques for solving PDEs include the following:...
can be used to approximately solve Maxwell's equations when an exact solution is impossible. These methods usually require a computer, and include the finite element methodFinite element methodThe finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
and finite-difference time-domain methodFinite-difference time-domain methodFinite-difference time-domain is one of the primary available computational electrodynamics modeling techniques. Since it is a time-domain method, FDTD solutions can cover a wide frequency range with a single simulation run, and treat nonlinear material properties in a natural way.The FDTD method...
. For more details, see Computational electromagneticsComputational electromagneticsComputational electromagnetics, computational electrodynamics or electromagnetic modeling is the process of modeling the interaction of electromagnetic fields with physical objects and the environment....
.
Gaussian units
Gaussian units is a popular electromagnetism variant of the centimetre gram second system of unitsCentimetre gram second system of unitsThe centimetre–gram–second system is a metric system of physical units based on centimetre as the unit of length, gram as a unit of mass, and second as a unit of time...
(cgs). In gaussian units, Maxwell's equations are:




where c is the speed of light in a vacuum. The microscopic equations are:




The relation between electric displacement field, electric fieldElectric fieldIn physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
and polarization densityPolarization densityIn classical electromagnetism, polarization density is the vector field that expresses the density of permanent or induced electric dipole moments in a dielectric material. When a dielectric is placed in an external electric field, its molecules gain electric dipole moment and the dielectric is...
is:
And likewise the relation between magnetic induction, magnetic fieldMagnetic fieldA magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
and total magnetizationMagnetizationIn classical electromagnetism, magnetization or magnetic polarization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material...
is:
In the linear approximation, the electric susceptibilityElectric susceptibilityIn electromagnetism, the electric susceptibility \chi_e is a dimensionless proportionality constant that indicates the degree of polarization of a dielectric material in response to an applied electric field...
and magnetic susceptibilityMagnetic susceptibilityIn electromagnetism, the magnetic susceptibility \chi_m is a dimensionless proportionality constant that indicates the degree of magnetization of a material in response to an applied magnetic field...
are defined so that:-
 ,
, 
(Note: although the susceptibilities are dimensionless numbers in both cgs and SI, they differ in value by a factor of 4π.)
The permittivityPermittivityIn electromagnetism, absolute permittivity is the measure of the resistance that is encountered when forming an electric field in a medium. In other words, permittivity is a measure of how an electric field affects, and is affected by, a dielectric medium. The permittivity of a medium describes how...
and permeability are:-
 ,
, 
so that-
 ,
, 
In vacuum, ε = μ = 1, therefore D = E, and B = H.
The force exerted upon a charged particle by the electric fieldElectric fieldIn physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
and magnetic fieldMagnetic fieldA magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
is given by the Lorentz forceLorentz forceIn physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
equation:
where q is the charge on the particle and v is the particle velocity. This is slightly different from the SISiSi, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
-unit expression above. For example, the magnetic field B has the same units as the electric field E.
Some equations in the article are given in Gaussian unitsGaussian unitsGaussian units comprise a metric system of physical units. This system is the most common of the several electromagnetic unit systems based on cgs units. It is also called the Gaussian unit system, Gaussian-cgs units, or often just cgs units...
but not SI or vice-versa. Fortunately, there are general rules to convert from one to the other; see the article Gaussian unitsGaussian unitsGaussian units comprise a metric system of physical units. This system is the most common of the several electromagnetic unit systems based on cgs units. It is also called the Gaussian unit system, Gaussian-cgs units, or often just cgs units...
for details.
Alternative formulations of Maxwell's equations
Special relativity motivated a compact mathematical formulation of Maxwell's equations, in terms of covariant tensors. Quantum mechanicsQuantum mechanicsQuantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
also motivated other formulations.
For example, consider a conductor moving in the field of a magnetMoving magnet and conductor problemThe moving magnet and conductor problem is a famous thought experiment, originating in the 19th century, concerning the intersection of classical electromagnetism and special relativity. In it, the current in a conductor moving with constant velocity, v, with respect to a magnet is calculated in...
. In the frame of the magnet, that conductor experiences a magnetic force. But in the frame of a conductor moving relative to the magnet, the conductor experiences a force due to an electric field. The following formulation shows how Maxwell's equations take the same form in any inertial coordinate system.
In terms of a minimum action principle
For the field formulation of Maxwell's equations in terms of a principle of extremal actionAction (physics)In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
, see the article on the electromagnetic tensor.
Covariant formulation of Maxwell's equations
In special relativity, in order to more clearly express the fact that Maxwell's ('microscopic') equations take the same form in any inertial coordinate system, Maxwell's equations are written in terms of four-vectorFour-vectorIn the theory of relativity, a four-vector is a vector in a four-dimensional real vector space, called Minkowski space. It differs from a vector in that it can be transformed by Lorentz transformations. The usage of the four-vector name tacitly assumes that its components refer to a standard basis...
s and tensors in the "manifestly covariantInvariant (physics)In mathematics and theoretical physics, an invariant is a property of a system which remains unchanged under some transformation.-Examples:In the current era, the immobility of polaris under the diurnal motion of the celestial sphere is a classical illustration of physical invariance.Another...
" form. The purely spatial components of the following are in SI units.
One ingredient in this formulation is the electromagnetic tensorElectromagnetic tensorThe electromagnetic tensor or electromagnetic field tensor is a mathematical object that describes the electromagnetic field of a physical system in Maxwell's theory of electromagnetism...
, a rank-2 covariant antisymmetric tensorTensorTensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
combining the electric and magnetic fields:
and the result of raising its indices
The other ingredient is the four-currentFour-currentIn special and general relativity, the four-current is the Lorentz covariant four-vector that replaces the electromagnetic current density, or indeed any conventional charge current density...
:
where ρ is the charge densityCharge densityThe linear, surface, or volume charge density is the amount of electric charge in a line, surface, or volume, respectively. It is measured in coulombs per meter , square meter , or cubic meter , respectively, and represented by the lowercase Greek letter Rho . Since there are positive as well as...
and J is the current densityCurrent densityCurrent density is a measure of the density of flow of a conserved charge. Usually the charge is the electric charge, in which case the associated current density is the electric current per unit area of cross section, but the term current density can also be applied to other conserved...
.
With these ingredients, Maxwell's equations can be written:
and
The first tensor equation is an expression of the two inhomogeneous Maxwell's equations, Gauss's lawGauss's lawIn physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:...
and Ampère's law with Maxwell's correction. The second equation is an expression of the two homogeneous equations, Faraday's law of inductionFaraday's law of inductionFaraday's law of induction dates from the 1830s, and is a basic law of electromagnetism relating to the operating principles of transformers, inductors, and many types of electrical motors and generators...
and Gauss's law for magnetism. The second equation is equivalent to
where is the contravariant version of the Levi-Civita symbolLevi-Civita symbolThe Levi-Civita symbol, also called the permutation symbol, antisymmetric symbol, or alternating symbol, is a mathematical symbol used in particular in tensor calculus...
is the contravariant version of the Levi-Civita symbolLevi-Civita symbolThe Levi-Civita symbol, also called the permutation symbol, antisymmetric symbol, or alternating symbol, is a mathematical symbol used in particular in tensor calculus...
, and
is the 4-gradientFour-gradientThe four-gradient is the four-vector generalization of the gradient:\partial_\alpha \ = \left...
. In the tensor equations above, repeated indices are summed over according to Einstein summation conventionEinstein notationIn mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...
. We have displayed the results in several common notations. Upper and lower components of a vector, vα and vα respectively, are interchanged with the fundamental tensor g, e.g., g = η = diag(−1, +1, +1, +1).
Alternative covariant presentations of Maxwell's equations also exist, for example in terms of the four-potential; see Covariant formulation of classical electromagnetism for details.
Potential formulation
In advanced classical mechanics and in quantum mechanics (where it is necessary) it is sometimes useful to express Maxwell's equations in a 'potential formulation' involving the electric potentialElectric potentialIn classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
(also called scalar potentialScalar potentialA scalar potential is a fundamental concept in vector analysis and physics . The scalar potential is an example of a scalar field...
), φ, and the magnetic potentialMagnetic potentialThe term magnetic potential can be used for either of two quantities in classical electromagnetism: the magnetic vector potential, A, and the magnetic scalar potential, ψ...
, A, (also called vector potentialVector potentialIn vector calculus, a vector potential is a vector field whose curl is a given vector field. This is analogous to a scalar potential, which is a scalar field whose negative gradient is a given vector field....
). These are defined such that:


With these definitions, the two homogeneous Maxwell's equations (Faraday's Law and Gauss's law for magnetism) are automatically satisfied and the other two (inhomogeneous) equations give the following equations (for "Maxwell's microscopic equations"):


These equations, taken together, are as powerful and complete as Maxwell's equations. Moreover, if we work only with the potentials and ignore the fields, the problem has been reduced somewhat, as the electric and magnetic fields each have three components which need to be solved for (six components altogether), while the electric and magnetic potentials have only four components altogether.
Many different choices of A and φ are consistent with a given E and B, making these choices physically equivalent – a flexibility known as gauge freedom. Suitable choice of A and φ can simplify these equations, or can adapt them to suit a particular situation.
Four-potential
In the Lorenz gauge, the two equations that represent the potentials can be reduced to one manifestly Lorentz invariant equation, using four-vectorFour-vectorIn the theory of relativity, a four-vector is a vector in a four-dimensional real vector space, called Minkowski space. It differs from a vector in that it can be transformed by Lorentz transformations. The usage of the four-vector name tacitly assumes that its components refer to a standard basis...
s: the four-currentFour-currentIn special and general relativity, the four-current is the Lorentz covariant four-vector that replaces the electromagnetic current density, or indeed any conventional charge current density...
defined by

formed from the current density j and charge density ρ, and the electromagnetic four-potentialElectromagnetic four-potentialThe electromagnetic four-potential is a potential from which the electromagnetic field can be derived. It combines both the electric scalar potential and the magnetic vector potential into a single space-time four-vector. In a given reference frame, the first component is the scalar potential and...
defined by

formed from the vector potential A and the scalar potential . The resulting single equation, due to Arnold SommerfeldArnold SommerfeldArnold Johannes Wilhelm Sommerfeld was a German theoretical physicist who pioneered developments in atomic and quantum physics, and also educated and groomed a large number of students for the new era of theoretical physics...
. The resulting single equation, due to Arnold SommerfeldArnold SommerfeldArnold Johannes Wilhelm Sommerfeld was a German theoretical physicist who pioneered developments in atomic and quantum physics, and also educated and groomed a large number of students for the new era of theoretical physics...
, a generalization of an equation due to Bernhard RiemannBernhard RiemannGeorg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
and known as the Riemann–Sommerfeld equation or the covariant form of the Maxwell equations, is:
 ,
,
where is the d'Alembertian operator, or four-Laplacian,
is the d'Alembertian operator, or four-Laplacian,  , sometimes written
, sometimes written  , or
, or  , where
, where  is the four-gradientFour-gradientThe four-gradient is the four-vector generalization of the gradient:\partial_\alpha \ = \left...
is the four-gradientFour-gradientThe four-gradient is the four-vector generalization of the gradient:\partial_\alpha \ = \left...
.
Differential geometric formulations
In free spaceVacuumIn everyday usage, vacuum is a volume of space that is essentially empty of matter, such that its gaseous pressure is much less than atmospheric pressure. The word comes from the Latin term for "empty". A perfect vacuum would be one with no particles in it at all, which is impossible to achieve in...
, where ε = ε0Electric constantThe physical constant ε0, commonly called the vacuum permittivity, permittivity of free space or electric constant is an ideal, physical constant, which is the value of the absolute dielectric permittivity of classical vacuum...
and μ = μ0 are constant everywhere, Maxwell's equations simplify considerably once the language of differential geometry and differential formDifferential formIn the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s is used. In what follows, cgs-Gaussian unitsGaussian unitsGaussian units comprise a metric system of physical units. This system is the most common of the several electromagnetic unit systems based on cgs units. It is also called the Gaussian unit system, Gaussian-cgs units, or often just cgs units...
, not SI units are used. (To convert to SI, see hereGaussian unitsGaussian units comprise a metric system of physical units. This system is the most common of the several electromagnetic unit systems based on cgs units. It is also called the Gaussian unit system, Gaussian-cgs units, or often just cgs units...
.) The electric and magnetic fields are now jointly described by a 2-formDifferential formIn the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
F in a 4-dimensional spacetimeSpacetimeIn physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
manifold. Maxwell's equations then reduce to
the Bianchi identity
where d denotes the exterior derivativeExterior derivativeIn differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
— a natural coordinate and metric independent differential operator acting on forms — and the source equation

where the (dual) Hodge star operator * is a linear transformation from the space of 2-forms to the space of (4-2)-forms defined by the metric in Minkowski spaceMinkowski spaceIn physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
(in four dimensions even by any metric conformalConformal geometryIn mathematics, conformal geometry is the study of the set of angle-preserving transformations on a space. In two real dimensions, conformal geometry is precisely the geometry of Riemann surfaces...
to this metric), and the fields are in natural unitsNatural unitsIn physics, natural units are physical units of measurement based only on universal physical constants. For example the elementary charge e is a natural unit of electric charge, or the speed of light c is a natural unit of speed...
where 1/4πε0 = 1. Here, the 3-form J is called the electric current form or current 3-form satisfying the continuity equationContinuity equationA continuity equation in physics is a differential equation that describes the transport of a conserved quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described...
The current 3-form can be integrated over a 3-dimensional space-time region. The physical interpretation of this integral is the charge in that region if it is spacelike, or the amount of charge that flows through a surface in a certain amount of time if that region is a spacelike surface cross a timelike interval.
As the exterior derivative is defined on any manifoldManifoldIn mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
, the differential form version of the Bianchi identity makes sense for any 4-dimensional manifold, whereas the source equation
is defined if the manifold is oriented and has a Lorentz metric. In particular the differential form version of the Maxwell equations are a convenient and intuitive formulation of the
Maxwell equations in general relativity.
In a linear, macroscopic theory, the influence of matter on the electromagnetic field is described through more general linear transformation in the space of 2-forms. We call
the constitutive transformation. The role of this transformation is comparable to the Hodge duality transformation. The Maxwell equations in the presence of matter then become:

where the current 3-form J still satisfies the continuity equation dJ = 0.
When the fields are expressed as linear combinations (of exterior products) of basis forms θp,
the constitutive relation takes the form
where the field coefficient functions are antisymmetric in the indices and the constitutive coefficients are antisymmetric in the corresponding pairs. In particular, the Hodge duality transformation leading to the vacuum equations discussed above are obtained by taking
which up to scaling is the only invariant tensor of this type that can be defined with the metric.
In this formulation, electromagnetism generalises immediately to any 4-dimensional oriented manifold or with small adaptations any manifold, requiring not even a metric.
Thus the expression of Maxwell's equations in terms of differential forms leads to a further notational and conceptual simplification. Whereas Maxwell's Equations could be written as two tensor equations instead of eight scalar equations, from which the propagation of electromagnetic disturbances and the continuity equation could be derived with a little effort, using differential forms leads to an even simpler derivation of these results.
Conceptual insight from this formulation
On the conceptual side, from the point of view of physics, this shows that the second and third Maxwell equations should be grouped together, be called the homogeneous ones, and be seen as geometric identities expressing nothing else than: the field F derives from a more "fundamental" potential A. While the first and last one should be seen as the dynamical equations of motion, obtained via the LagrangianLagrangianThe Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
principle of least action, from the "interaction term" A J (introduced through gaugeGauge theoryIn physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
covariant derivativeCovariant derivativeIn mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
s), coupling the field to matter.
Often, the time derivative in the third law motivates calling this equation "dynamical", which is somewhat misleading; in the sense of the preceding analysis, this is rather an artifact of breaking relativisticSpecial relativitySpecial relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
covarianceCovarianceIn probability theory and statistics, covariance is a measure of how much two variables change together. Variance is a special case of the covariance when the two variables are identical.- Definition :...
by choosing a preferred time direction. To have physical degrees of freedom propagated by these field equations, one must include a kinetic termKinetic termIn physics, a kinetic term is the part of the Lagrangian that is bilinear in the fields , and usually contains two derivatives with respect to time ; in the case of fermions, the kinetic term usually has one derivative only...
F *F for A; and take into account the non-physical degrees of freedom which can be removed by gauge transformation A → A' = A − dα. See also gauge fixingGauge fixingIn the physics of gauge theories, gauge fixing denotes a mathematical procedure for coping with redundant degrees of freedom in field variables. By definition, a gauge theory represents each physically distinct configuration of the system as an equivalence class of detailed local field...
and Faddeev–Popov ghosts.
Geometric algebra (GA) formulation
In geometric algebraGeometric algebraGeometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
, Maxwell's equations are reduced to a single equation,

where F and J are multivectors

and
with the unit pseudoscalarPseudoscalarIn physics, a pseudoscalar is a quantity that behaves like a scalar, except that it changes sign under a parity inversion such as improper rotations while a true scalar does not.The prototypical example of a pseudoscalar is the scalar triple product...
I2 = −1
The GA spatial gradient operator ∇ acts on a vector field, such that

In spacetime algebraSpacetime algebraIn mathematical physics, spacetime algebra is a name for the Clifford algebra Cℓ1,3,or Geometric algebra G4 = G which can be particularly closely associated with the geometry of special relativity and relativistic spacetime....
using the same geometric product the equation is simply

the spacetime derivative of the electromagnetic field is its source. Here the (non-bold) spacetime gradient

is a four vector, as is the current density

For a demonstration that the equations given reproduce Maxwell's equations see the main article.
Classical electrodynamics as the curvature of a line bundle
An elegant and intuitive way to formulate Maxwell's equations is to use complex line bundleLine bundleIn mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
s or principal bundlePrincipal bundleIn mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
s with fibre U(1). The connectionConnection (mathematics)In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
 on the line bundle has a curvatureCurvatureIn mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
on the line bundle has a curvatureCurvatureIn mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
 which is a two-form that automatically satisfies
which is a two-form that automatically satisfies  and can be interpreted as a field-strength. If the line bundle is trivial with flat reference connection d we can write
and can be interpreted as a field-strength. If the line bundle is trivial with flat reference connection d we can write  and F = dA with A the 1-formDifferential formIn the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
and F = dA with A the 1-formDifferential formIn the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
composed of the electric potentialElectric potentialIn classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
and the magnetic vector potential.
In quantum mechanics, the connection itself is used to define the dynamics of the system. This formulation allows a natural description of the Aharonov–Bohm effect. In this experiment, a static magnetic field runs through a long magnetic wire (e.g., an iron wire magnetized longitudinally). Outside of this wire the magnetic induction is zero, in contrast to the vector potential, which essentially depends on the magnetic flux through the cross-section of the wire and does not vanish outside. Since there is no electric field either, the Maxwell tensor F = 0 throughout the space-time region outside the tube, during the experiment. This means by definition that the connection is flat there.
is flat there.
However, as mentioned, the connection depends on the magnetic field through the tube since the holonomyHolonomyIn differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...
along a non-contractible curve encircling the tube is the magnetic flux through the tube in the proper units. This can be detected quantum-mechanically with a double-slit electron diffraction experiment on an electron wave traveling around the tube. The holonomy corresponds to an extra phase shift, which leads to a shift in the diffraction pattern.
Traditional formulation
Matter and energy generate curvature of spacetimeSpacetimeIn physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
. This is the subject of general relativityGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
. Curvature of spacetime affects electrodynamics. An electromagnetic field having energy and momentum also generates curvature in spacetime. Maxwell's equations in curved spacetime can be obtained by replacing the derivatives in the equations in flat spacetime with covariant derivativeCovariant derivativeIn mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
s. (Whether this is the appropriate generalization requires separate investigation.) The sourced and source-free equations become (cgs-Gaussian unitsGaussian unitsGaussian units comprise a metric system of physical units. This system is the most common of the several electromagnetic unit systems based on cgs units. It is also called the Gaussian unit system, Gaussian-cgs units, or often just cgs units...
):

and

Here,

is a Christoffel symbol that characterizes the curvature of spacetime and ∇α is the covariant derivative.
Formulation in terms of differential forms
The formulation of the Maxwell equations in terms of differential formDifferential formIn the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s can be used without change in general relativity. The equivalence of the more traditional general relativistic formulation using the covariant derivative with the differential form formulation can be seen as follows. Choose local coordinates xα which gives a basis of 1-forms dxα in every point of the open set where the coordinates are defined. Using this basis and cgs-Gaussian unitsGaussian unitsGaussian units comprise a metric system of physical units. This system is the most common of the several electromagnetic unit systems based on cgs units. It is also called the Gaussian unit system, Gaussian-cgs units, or often just cgs units...
we define
- The antisymmetric infinitesimal field tensor
 , corresponding to the field 2-form F
, corresponding to the field 2-form F
- The current-vector infinitesimal 3-form J

Here g is as usual the determinant of the metric tensor .
.
A small computation that uses the symmetry of the Christoffel symbolsChristoffel symbolsIn mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
(i.e., the torsion-freeness of the Levi-Civita connectionLevi-Civita connectionIn Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
) and the covariant constantness of the Hodge star operator
then shows that in this coordinate neighborhood we have:
- the Bianchi identity

- the source equation

- the continuity equation

See also
Journal articles
- James Clerk MaxwellJames Clerk MaxwellJames Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
, "A Dynamical Theory of the Electromagnetic FieldA Dynamical Theory of the Electromagnetic Field"A Dynamical Theory of the Electromagnetic Field" is the third of James Clerk Maxwell's papers regarding electromagnetism, published in 1865. It is the paper in which the original set of four Maxwell's equations first appeared...
", Philosophical Transactions of the Royal Society of London 155, 459-512 (1865). (This article accompanied a December 8, 1864 presentation by Maxwell to the Royal Society.)
The developments before relativity- Joseph LarmorJoseph LarmorSir Joseph Larmor , a physicist and mathematician who made innovations in the understanding of electricity, dynamics, thermodynamics, and the electron theory of matter...
(1897) "On a dynamical theory of the electric and luminiferous medium", Phil. Trans. Roy. Soc. 190, 205-300 (third and last in a series of papers with the same name). - Hendrik LorentzHendrik LorentzHendrik Antoon Lorentz was a Dutch physicist who shared the 1902 Nobel Prize in Physics with Pieter Zeeman for the discovery and theoretical explanation of the Zeeman effect...
(1899) "Simplified theory of electrical and optical phenomena in moving systems", Proc. Acad. Science Amsterdam, I, 427-43. - Hendrik LorentzHendrik LorentzHendrik Antoon Lorentz was a Dutch physicist who shared the 1902 Nobel Prize in Physics with Pieter Zeeman for the discovery and theoretical explanation of the Zeeman effect...
(1904) "Electromagnetic phenomena in a system moving with any velocity less than that of light", Proc. Acad. Science Amsterdam, IV, 669-78. - Henri PoincaréHenri PoincaréJules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
(1900) "La theorie de Lorentz et la Principe de Reaction", Archives Néerlandaises, V, 253-78. - Henri PoincaréHenri PoincaréJules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
(1901) Science and Hypothesis - Henri PoincaréHenri PoincaréJules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
(1905) "Sur la dynamique de l'électron", Comptes rendus de l'Académie des Sciences, 140, 1504-8.
see
Computational techniques
Chapter 8 sets out several variants of the equations using exterior algebraExterior algebraIn mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
and differential formDifferential formIn the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s.
External links
- Mathematical aspects of Maxwell's equation are discussed on the Dispersive PDE Wiki.
Modern treatments
- Electromagnetism, B. Crowell, Fullerton College
- Lecture series: Relativity and electromagnetism, R. Fitzpatrick, University of Texas at Austin
- Electromagnetic waves from Maxwell's equations on Project PHYSNET.
- MIT Video Lecture Series (36 x 50 minute lectures) (in .mp4 format) - Electricity and Magnetism Taught by Professor Walter LewinWalter LewinWalter H. G. Lewin is a professor emeritus of physics at the Massachusetts Institute of Technology .-Education and career:...
.
Historical
- James Clerk Maxwell, A Treatise on Electricity And Magnetism Vols 1 and 2 1904—most readable edition with all corrections—Antique Books Collection suitable for free reading online.
- Maxwell, J.C., A Treatise on Electricity And Magnetism - Volume 1 - 1873 - Posner Memorial Collection - Carnegie Mellon University
- Maxwell, J.C., A Treatise on Electricity And Magnetism - Volume 2 - 1873 - Posner Memorial Collection - Carnegie Mellon University
- On Faraday's Lines of Force - 1855/56 Maxwell's first paper (Part 1 & 2) - Compiled by Blaze Labs Research (PDF)
- On Physical Lines of Force - 1861 Maxwell's 1861 paper describing magnetic lines of Force - Predecessor to 1873 Treatise
- Maxwell, James Clerk, "A Dynamical Theory of the Electromagnetic Field", Philosophical Transactions of the Royal Society of London 155, 459-512 (1865). (This article accompanied a December 8, 1864 presentation by Maxwell to the Royal Society.)
- Catt, Walton and Davidson. "The History of Displacement Current". Wireless World, March 1979.
- Reprint from Dover Publications (ISBN 0-486-60636-8)
- Full text of 1904 Edition including full text search.
- A Dynamical Theory Of The Electromagnetic Field - 1865 Maxwell's 1865 paper describing his 20 Equations in 20 Unknowns - Predecessor to the 1873 Treatise
Other
- in which the permittivity and permeability functions are replaced by integrals over the more general electric




