Line integral
Encyclopedia
In mathematics
, a line integral (sometimes called a path integral, contour integral, or curve integral; not to be confused with calculating arc length using integration
) is an integral
where the function
to be integrated is evaluated along a curve
.
The function to be integrated may be a scalar field
or a vector field
. The value of the line integral is the sum of values of the field at all points on the curve, weighted by some scalar function on the curve (commonly arc length
or, for a vector field, the scalar product
of the vector field with a differential vector in the curve). This weighting distinguishes the line integral from simpler integrals defined on intervals
. Many simple formulae in physics (for example
, W=F·s) have natural continuous analogs in terms of line integrals (W=∫C F· ds). The line integral finds the work
done on an object moving through an electric or gravitational field, for example.
along a given curve. More specifically, the line integral over a scalar field can be interpreted as the area under the field carved out by a particular curve. This can be visualised as the surface created by z = f(x,y) and a curve C in the x-y plane. The line integral of f would be the area of the "curtain" created when the points of the surface that are directly over C are carved out.
f : U ⊆ Rn → R, the line integral along a piecewise smooth curve
C ⊂ U is defined as
where r: [a, b] → C is an arbitrary bijective parametrization
of the curve C such that r(a) and r(b) give the endpoints of C.
The function f is called the integrand, the curve C is the domain of integration, and the symbol ds may be intuitively interpreted as an elementary arc length
. Line integrals of scalar fields over a curve C do not depend on the chosen parametrization r of C.
using the above definitions of f, C and a parametrization r of C. This can be done by partitioning the interval
[a,b] into n sub-intervals [ti-1, ti] of length Δt = (b − a)/n, then r(ti) denotes some point, call it a sample point, on the curve C. We can use the set of sample points {r(ti) : 1 ≤ i ≤ n} to approximate the curve C by a polygonal path by introducing a straight line piece between each of the sample points r(ti-1) and r(ti). We then label the distance between each of the sample points on the curve as Δsi. The product of f(r(ti)) and Δsi can be associated with the signed area of a rectangle with a height and width of f(r(ti)) and Δsi respectively. Taking the limit
of the sum
of the terms as the length of the partitions approaches zero gives us Ġ
We note that the distance between subsequent points on the curve, is
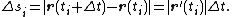
Substituting this in to our above Riemann sum yields
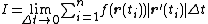
which is the Riemann sum for the integral
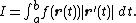
Basically is the area under the constraint of the scalar function z=f(x,y), where x=u(t) and y=v(t) is the constraint.
F : U ⊆ Rn → Rn, the line integral along a piecewise smooth curve
C ⊂ U, in the direction of r, is defined as
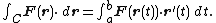
where · is the dot product
and r: [a, b] → C is a bijective parametrization
of the curve C such that r(a) and r(b) give the endpoints of C.
A line integral of a scalar field is thus a line integral of a vector field where the vectors are always tangential to the line.
Line integrals of vector fields are independent of the parametrization r in absolute value
, but they do depend on its orientation
. Specifically, a reversal in the orientation of the parametrization changes the sign of the line integral.
The line integral of a vector field can be derived in a very similar manner as in the case of a scalar field. Again using the above definitions of F, C and its parametrization r(t), we construct the integral from a Riemann sum
. Partition the interval [a,b] into n intervals of length Δt = (b − a)/n. Letting ti be the ith point on [a,b], then r(ti) gives us the position of the ith point on the curve. However, instead of calculating up the distances between subsequent points, we need to calculate their displacement
vectors, Δsi. As before, evaluating F at all the points on the radiation curve and taking the dot product with each displacement vector which gives us the infinitesimal
contribution of each partition of F on C. Letting the size of the partitions go to zero gives us a sum
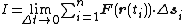
We see that the displacement vector between adjacent points on the curve is
Substituting this into our above Riemann sum yields
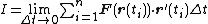
which is the Riemann sum for the integral defined above.
of a scalar field
G (i.e. if F is conservative), that is,
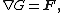
then the derivative
of the composition
of G and r(t) is
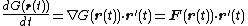
which happens to be the integrand for the line integral of F on r(t). It follows that, given a path C , then
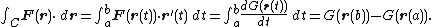
In other words, the integral of F over C depends solely on the values of G in the points r(b) and r(a) and is thus independent of the path between them.
For this reason, a line integral of a conservative vector field is called path independent.
. Suppose U is an open subset of C
, γ : [a, b] → U is a rectifiable curve and f : U → C is a function. Then the line integral
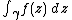
may be defined by subdividing the interval
[a, b] into a = t0 < t1 < ... < tn = b and considering the expression
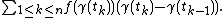
The integral is then the limit
of this sum, as the lengths of the subdivision intervals approach zero.
If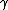
is a continuously differentiable curve, the line integral can be evaluated as an integral of a function of a real variable:
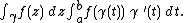
When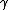
is a closed curve, that is, its initial and final points coincide, the notation
is often used for the line integral of f along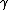
.
The line integrals of complex functions can be evaluated using a number of techniques: the integral may be split into real and imaginary parts reducing the problem to that of evaluating two real-valued line integrals, the Cauchy integral formula may be used in other circumstances. If the line integral is a closed curve in a region where the function is analytic
and containing no singularities
, then the value of the integral is simply zero; this is a consequence of the Cauchy integral theorem. Because of the residue theorem
, one can often use contour integrals in the complex plane to find integrals of real-valued functions of a real variable (see residue theorem
for an example).
about 0, which can be parametrized by eit, with t in [0, 2π]. Substituting, we find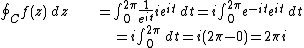
where we use the fact that any complex number z can be written as reit where r is the modulus
of z. On the unit circle this is fixed to 1, so the only variable left is the angle, which is denoted by t. This answer can be also verified by the Cauchy integral formula.
of the corresponding complex function of a complex variable. More specifically, if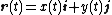
and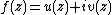 
, then:
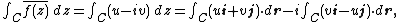
provided that both integrals on the right hand side exist, and that the parametrization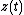
of C has the same orientation as 
.
Due to the Cauchy-Riemann equations
the curl of the vector field corresponding to the conjugate of a holomorphic function
is zero. This relates through Stokes' theorem
both types of line integral being zero.
" of quantum mechanics
actually refers not to path integrals in this sense but to functional integrals
, that is, integrals over a space of paths, of a function of a possible path. However, path integrals in the sense of this article are important in quantum mechanics; for example, complex contour integration is often used in evaluating probability
amplitude
s in quantum scattering
theory.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a line integral (sometimes called a path integral, contour integral, or curve integral; not to be confused with calculating arc length using integration
Arc length
Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
) is an integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
where the function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
to be integrated is evaluated along a curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
.
The function to be integrated may be a scalar field
Scalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
or a vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
. The value of the line integral is the sum of values of the field at all points on the curve, weighted by some scalar function on the curve (commonly arc length
Arc length
Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
or, for a vector field, the scalar product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
of the vector field with a differential vector in the curve). This weighting distinguishes the line integral from simpler integrals defined on intervals
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
. Many simple formulae in physics (for example
Mechanical work
In physics, work is a scalar quantity that can be described as the product of a force times the distance through which it acts, and it is called the work of the force. Only the component of a force in the direction of the movement of its point of application does work...
, W=F·s) have natural continuous analogs in terms of line integrals (W=∫C F· ds). The line integral finds the work
Mechanical work
In physics, work is a scalar quantity that can be described as the product of a force times the distance through which it acts, and it is called the work of the force. Only the component of a force in the direction of the movement of its point of application does work...
done on an object moving through an electric or gravitational field, for example.
Vector calculus
In qualitative terms, a line integral in vector calculus can be thought of as a measure of the total effect of a given fieldField (physics)
In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
along a given curve. More specifically, the line integral over a scalar field can be interpreted as the area under the field carved out by a particular curve. This can be visualised as the surface created by z = f(x,y) and a curve C in the x-y plane. The line integral of f would be the area of the "curtain" created when the points of the surface that are directly over C are carved out.
Definition
For some scalar fieldScalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
f : U ⊆ Rn → R, the line integral along a piecewise smooth curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
C ⊂ U is defined as
where r: [a, b] → C is an arbitrary bijective parametrization
Parametric equation
In mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example is when one uses a time parameter to determine the position, velocity, and other information about a body in motion....
of the curve C such that r(a) and r(b) give the endpoints of C.
The function f is called the integrand, the curve C is the domain of integration, and the symbol ds may be intuitively interpreted as an elementary arc length
Arc length
Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
. Line integrals of scalar fields over a curve C do not depend on the chosen parametrization r of C.
Derivation
For a line integral over a scalar field, the integral can be constructed from a Riemann sumRiemann sum
In mathematics, a Riemann sum is a method for approximating the total area underneath a curve on a graph, otherwise known as an integral. It mayalso be used to define the integration operation. The method was named after German mathematician Bernhard Riemann....
using the above definitions of f, C and a parametrization r of C. This can be done by partitioning the interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
[a,b] into n sub-intervals [ti-1, ti] of length Δt = (b − a)/n, then r(ti) denotes some point, call it a sample point, on the curve C. We can use the set of sample points {r(ti) : 1 ≤ i ≤ n} to approximate the curve C by a polygonal path by introducing a straight line piece between each of the sample points r(ti-1) and r(ti). We then label the distance between each of the sample points on the curve as Δsi. The product of f(r(ti)) and Δsi can be associated with the signed area of a rectangle with a height and width of f(r(ti)) and Δsi respectively. Taking the limit
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
of the sum
SUM
SUM can refer to:* The State University of Management* Soccer United Marketing* Society for the Establishment of Useful Manufactures* StartUp-Manager* Software User’s Manual,as from DOD-STD-2 167A, and MIL-STD-498...
of the terms as the length of the partitions approaches zero gives us Ġ
We note that the distance between subsequent points on the curve, is
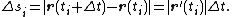
Substituting this in to our above Riemann sum yields
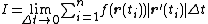
which is the Riemann sum for the integral
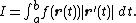
Basically is the area under the constraint of the scalar function z=f(x,y), where x=u(t) and y=v(t) is the constraint.
Definition
For a vector fieldVector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
F : U ⊆ Rn → Rn, the line integral along a piecewise smooth curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
C ⊂ U, in the direction of r, is defined as
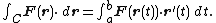
where · is the dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
and r: [a, b] → C is a bijective parametrization
Parametric equation
In mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example is when one uses a time parameter to determine the position, velocity, and other information about a body in motion....
of the curve C such that r(a) and r(b) give the endpoints of C.
A line integral of a scalar field is thus a line integral of a vector field where the vectors are always tangential to the line.
Line integrals of vector fields are independent of the parametrization r in absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
, but they do depend on its orientation
Curve orientation
In mathematics, a positively oriented curve is a planar simple closed curve such that when traveling on it one always has the curve interior to the left...
. Specifically, a reversal in the orientation of the parametrization changes the sign of the line integral.
Derivation
Riemann sum
In mathematics, a Riemann sum is a method for approximating the total area underneath a curve on a graph, otherwise known as an integral. It mayalso be used to define the integration operation. The method was named after German mathematician Bernhard Riemann....
. Partition the interval [a,b] into n intervals of length Δt = (b − a)/n. Letting ti be the ith point on [a,b], then r(ti) gives us the position of the ith point on the curve. However, instead of calculating up the distances between subsequent points, we need to calculate their displacement
Displacement (vector)
A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P...
vectors, Δsi. As before, evaluating F at all the points on the radiation curve and taking the dot product with each displacement vector which gives us the infinitesimal
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
contribution of each partition of F on C. Letting the size of the partitions go to zero gives us a sum
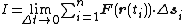
We see that the displacement vector between adjacent points on the curve is
Substituting this into our above Riemann sum yields
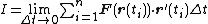
which is the Riemann sum for the integral defined above.
Path independence
If a vector field F is the gradientGradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of a scalar field
Scalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
G (i.e. if F is conservative), that is,
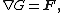
then the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of the composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
of G and r(t) is
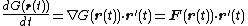
which happens to be the integrand for the line integral of F on r(t). It follows that, given a path C , then
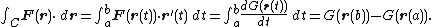
In other words, the integral of F over C depends solely on the values of G in the points r(b) and r(a) and is thus independent of the path between them.
For this reason, a line integral of a conservative vector field is called path independent.
Applications
The line integral has many uses in physics. For example, the work done on a particle traveling on a curve C inside a force field represented as a vector field F is the line integral of F on C.Complex line integral
The line integral is a fundamental tool in complex analysisComplex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
. Suppose U is an open subset of C
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
, γ : [a, b] → U is a rectifiable curve and f : U → C is a function. Then the line integral
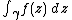
may be defined by subdividing the interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
[a, b] into a = t0 < t1 < ... < tn = b and considering the expression
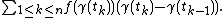
The integral is then the limit
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
of this sum, as the lengths of the subdivision intervals approach zero.
If
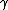is a continuously differentiable curve, the line integral can be evaluated as an integral of a function of a real variable: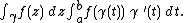When
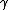is a closed curve, that is, its initial and final points coincide, the notationis often used for the line integral of f along
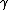.The line integrals of complex functions can be evaluated using a number of techniques: the integral may be split into real and imaginary parts reducing the problem to that of evaluating two real-valued line integrals, the Cauchy integral formula may be used in other circumstances. If the line integral is a closed curve in a region where the function is analytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
and containing no singularities
Mathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
, then the value of the integral is simply zero; this is a consequence of the Cauchy integral theorem. Because of the residue theorem
Residue theorem
The residue theorem, sometimes called Cauchy's Residue Theorem, in complex analysis is a powerful tool to evaluate line integrals of analytic functions over closed curves and can often be used to compute real integrals as well. It generalizes the Cauchy integral theorem and Cauchy's integral formula...
, one can often use contour integrals in the complex plane to find integrals of real-valued functions of a real variable (see residue theorem
Residue theorem
The residue theorem, sometimes called Cauchy's Residue Theorem, in complex analysis is a powerful tool to evaluate line integrals of analytic functions over closed curves and can often be used to compute real integrals as well. It generalizes the Cauchy integral theorem and Cauchy's integral formula...
for an example).
Example
Consider the function f(z)=1/z, and let the contour C be the unit circleUnit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
about 0, which can be parametrized by eit, with t in [0, 2π]. Substituting, we find
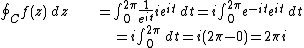
where we use the fact that any complex number z can be written as reit where r is the modulus
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of z. On the unit circle this is fixed to 1, so the only variable left is the angle, which is denoted by t. This answer can be also verified by the Cauchy integral formula.
Relation between the line integral of a vector field and the complex line integral
Viewing complex numbers as 2-dimensional vectors, the line integral of a 2-dimensional vector field corresponds to the real part of the line integral of the conjugateComplex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
of the corresponding complex function of a complex variable. More specifically, if
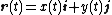and 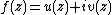, then: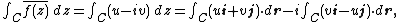provided that both integrals on the right hand side exist, and that the parametrization
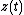of C has the same orientation as .Due to the Cauchy-Riemann equations
Cauchy-Riemann equations
In mathematics, the Cauchy–Riemann differential equations in complex analysis, named after Augustin Cauchy and Bernhard Riemann, consist of a system of two partial differential equations which must be satisfied if we know that a complex function is complex differentiable...
the curl of the vector field corresponding to the conjugate of a holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
is zero. This relates through Stokes' theorem
Stokes' theorem
In differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
both types of line integral being zero.
Quantum mechanics
The "path integral formulationPath integral formulation
The path integral formulation of quantum mechanics is a description of quantum theory which generalizes the action principle of classical mechanics...
" of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
actually refers not to path integrals in this sense but to functional integrals
Functional integration
Functional integration is a collection of results in mathematics and physics where the domain of an integral is no longer a region of space, but a space of functions...
, that is, integrals over a space of paths, of a function of a possible path. However, path integrals in the sense of this article are important in quantum mechanics; for example, complex contour integration is often used in evaluating probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
s in quantum scattering
Scattering
Scattering is a general physical process where some forms of radiation, such as light, sound, or moving particles, are forced to deviate from a straight trajectory by one or more localized non-uniformities in the medium through which they pass. In conventional use, this also includes deviation of...
theory.
See also
- Arc lengthArc lengthDetermining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
- Green's theoremGreen's theoremIn mathematics, Green's theorem gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C...
- Stokes' theoremStokes' theoremIn differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
- Methods of contour integrationMethods of contour integrationIn the mathematical field of complex analysis, contour integration is a method of evaluating certain integrals along paths in the complex plane.Contour integration is closely related to the calculus of residues, a methodology of complex analysis....
- Surface integralSurface integralIn mathematics, a surface integral is a definite integral taken over a surface ; it can be thought of as the double integral analog of the line integral...
- Volume integralVolume integralIn mathematics — in particular, in multivariable calculus — a volume integral refers to an integral over a 3-dimensional domain....
- Divergence theoremDivergence theoremIn vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
- Nachbin's theoremNachbin's theoremIn mathematics, in the area of complex analysis, Nachbin's theorem is commonly used to establish a bound on the growth rates for an analytic function. This article will provide a brief review of growth rates, including the idea of a function of exponential type...
- Functional integrationFunctional integrationFunctional integration is a collection of results in mathematics and physics where the domain of an integral is no longer a region of space, but a space of functions...
External links
- Khan AcademyKhan AcademyThe Khan Academy is a not-for-profit educational organization, created in 2006 by Bangladeshi American educator Salman Khan, a graduate of MIT. With the stated mission of "providing a high quality education to anyone, anywhere", the website supplies a free online collection of more than 2,700 micro...
Lesson 1 Lesson 2 - A pictoral explanation of the path integral
- Contour Integrals Module by John H. Mathews
- Line integral of a vector field - Interactive