
Lagrangian
Encyclopedia
The Lagrangian, L, of a dynamical system
is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange
. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics
by Irish mathematician William Rowan Hamilton
known as Lagrangian mechanics
. In classical mechanics, the Lagrangian is defined as the kinetic energy
, , of the system minus its potential energy
, of the system minus its potential energy
, . In symbols,
. In symbols,

Under conditions that are given in Lagrangian mechanics
, if the Lagrangian of a system is known, then the equations of motion
of the system may be obtained by a direct substitution of the expression for the Lagrangian into the Euler–Lagrange equation, a particular family of partial differential equation
s.
. Although Lagrange only sought to describe classical mechanics
, the action principle that is used to derive the Lagrange equation was later recognized to be applicable to quantum mechanics
as well.
Physical action
and quantum-mechanical phase
are related via Planck's constant, and the principle of stationary action can be understood in terms of constructive interference of wave functions.
The same principle, and the Lagrangian formalism, are tied closely to Noether's theorem
, which connect physical conserved quantities
to continuous symmetries
of a physical system.
Lagrangian mechanics and Noether's theorem
together yield a natural formalism for first quantization
by including commutators between certain terms of the Lagrangian equations of motion for a physical system.
An important property of the Lagrangian is that conservation laws can easily be read off from it. For example, if the Lagrangian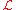 depends on the time-derivative
depends on the time-derivative 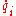 of a generalized coordinate, but not on
of a generalized coordinate, but not on 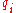 itself, then the generalized momentum,
itself, then the generalized momentum,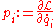 ,
,
is a conserved quantity. This is a special case of Noether's theorem
. Such coordinates are called "cyclic".
For example, the conservation of the generalized momentum,
say, can be directly seen if the Lagrangian of the system is of the form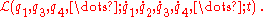
Also, if the time, t, does not appear in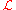 , then the conservation of the Hamiltonian
, then the conservation of the Hamiltonian
follows. This is the energy conservation unless the potential energy depends on velocity, as in electrodynamics. More details can be found in any textbook on theoretical mechanics.
are obtained by means of an action
principle, written as:

where the action,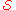 , is a functional
, is a functional
of the dependent variables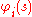 with their derivatives and s itself
with their derivatives and s itself

and where denotes the set of n independent variable
denotes the set of n independent variable
s of the system, indexed by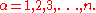
The equations of motion obtained from this functional derivative
are the Euler–Lagrange equations of this action. For example, in the classical mechanics
of particles, the only independent variable is time, t. So the Euler-Lagrange equations are
Dynamical systems whose equations of motion are obtainable by means of an action principle on a suitably chosen Lagrangian are known as Lagrangian dynamical systems. Examples of Lagrangian dynamical systems range from the classical version of the Standard Model
, to Newton's equations, to purely mathematical problems such as geodesic
equations and Plateau's problem
.
and the Lagrangian
 .
.
Then, the Euler–Lagrange equation is:

where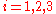 .
.
The derivation yields:
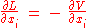

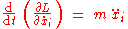
The Euler–Lagrange equations can therefore be written as:

where the time derivative is written conventionally as a dot above the quantity being differentiated, and is the del operator
is the del operator
.
Using this result, it can easily be shown that the Lagrangian approach is equivalent to the Newtonian one.
If the force is written in terms of the potential ; the resulting equation is
; the resulting equation is  , which is exactly the same equation as in a Newtonian approach for a constant mass object.
, which is exactly the same equation as in a Newtonian approach for a constant mass object.
A very similar deduction gives us the expression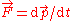 , which is Newton's Second Law in its general form.
, which is Newton's Second Law in its general form.
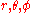 with the Lagrangian
with the Lagrangian

Then the Euler–Lagrange equations are:


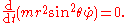
Here the set of parameters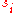 is just the time
is just the time  , and the dynamical variables
, and the dynamical variables  are the trajectories
are the trajectories 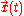 of the particle.
of the particle.
Despite the use of standard variables such as , the Lagrangian allows the use of any coordinates, which do not need to be orthogonal. These are "generalized coordinates
, the Lagrangian allows the use of any coordinates, which do not need to be orthogonal. These are "generalized coordinates
".
 kilograms, and position
kilograms, and position  meters in a Newtonian gravitation field with potential
meters in a Newtonian gravitation field with potential  joules per kilogram. The particle's world line is parameterized by time
joules per kilogram. The particle's world line is parameterized by time  seconds. The particle's kinetic energy is:
seconds. The particle's kinetic energy is:

and the particle's gravitational potential energy is:
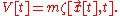
Then its Lagrangian is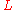 joules where
joules where
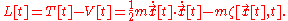
Varying in the integral (equivalent to the Euler–Lagrange differential equation), we get
in the integral (equivalent to the Euler–Lagrange differential equation), we get
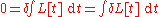

Integrate the first term by parts and discard the total integral. Then divide out the variation to get
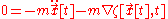
and thus

is the equation of motion — two different expressions for the force.

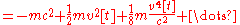
(In special relativity, the energy of a free test particle is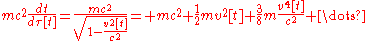 )
)
where meters per second is the speed of light
meters per second is the speed of light
in vacuum, seconds is the proper time (i.e. time measured by a clock moving with the particle) and
seconds is the proper time (i.e. time measured by a clock moving with the particle) and  The second term in the series is just the classical kinetic energy. Suppose the particle has electrical charge
The second term in the series is just the classical kinetic energy. Suppose the particle has electrical charge 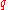 coulombs and is in an electromagnetic field with scalar potential
coulombs and is in an electromagnetic field with scalar potential
 volts (a volt is a joule per coulomb) and vector potential
volts (a volt is a joule per coulomb) and vector potential
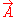 volt seconds per meter. The Lagrangian of a special relativistic test particle in an electromagnetic field is:
volt seconds per meter. The Lagrangian of a special relativistic test particle in an electromagnetic field is:
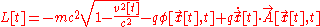
Varying this with respect to , we get
, we get

which is

which is the equation for the Lorentz force
where
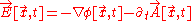

, the first term generalizes (includes) both the classical kinetic energy and interaction with the Newtonian gravitational potential. It becomes:

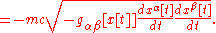
The Lagrangian of a general relativistic test particle in an electromagnetic field is:
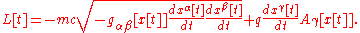
If the four space-time coordinates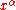 are given in arbitrary units (i.e. unit-less), then
are given in arbitrary units (i.e. unit-less), then  meters squared is the rank 2 symmetric metric tensor
meters squared is the rank 2 symmetric metric tensor
which is also the gravitational potential. Also,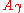 volt seconds is the electromagnetic 4-vector potential. Notice that a factor of c has been absorbed into the square root because it is the equivalent of
volt seconds is the electromagnetic 4-vector potential. Notice that a factor of c has been absorbed into the square root because it is the equivalent of
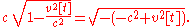
Note that this notion has been directly generalized from special relativity
denoted by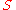 .
.
In field theory, a distinction is occasionally made between the Lagrangian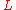 , of which the action is the time integral:
, of which the action is the time integral:

and the Lagrangian density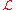 , which one integrates over all space-time to get the action:
, which one integrates over all space-time to get the action:
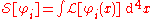
The Lagrangian is then the spatial integral of the Lagrangian density. However,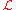 is also frequently simply called the Lagrangian, especially in modern use; it is far more useful in relativistic
is also frequently simply called the Lagrangian, especially in modern use; it is far more useful in relativistic
theories since it is a locally
defined, Lorentz
scalar
field. Both definitions of the Lagrangian can be seen as special cases of the general form, depending on whether the spatial variable is incorporated into the index
is incorporated into the index 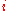 or the parameters
or the parameters  in
in 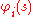 . Quantum field theories
. Quantum field theories
in particle physics
, such as quantum electrodynamics
, are usually described in terms of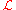 , and the terms in this form of the Lagrangian translate quickly to the rules used in evaluating Feynman diagram
, and the terms in this form of the Lagrangian translate quickly to the rules used in evaluating Feynman diagram
s.
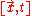 . For example, in the case of Newtonian gravity, the Lagrangian density integrated over space-time gives you an equation which, if solved, would yield
. For example, in the case of Newtonian gravity, the Lagrangian density integrated over space-time gives you an equation which, if solved, would yield 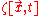 . This
. This 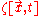 , when substituted back in equation (1), the Lagrangian equation for the test particle in a Newtonian gravitational field, provides the information needed to calculate the acceleration of the particle.
, when substituted back in equation (1), the Lagrangian equation for the test particle in a Newtonian gravitational field, provides the information needed to calculate the acceleration of the particle.
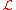 joules per cubic meter. The interaction term
joules per cubic meter. The interaction term 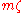 is replaced by a term involving a continuous mass density
is replaced by a term involving a continuous mass density  kilograms per cubic meter. This is necessary because using a point source for a field would result in mathematical difficulties. The resulting Lagrangian for the classical gravitational field is:
kilograms per cubic meter. This is necessary because using a point source for a field would result in mathematical difficulties. The resulting Lagrangian for the classical gravitational field is:
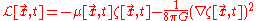
where meters cubed per kilogram second squared is the gravitational constant
meters cubed per kilogram second squared is the gravitational constant
. Variation of the integral with respect to gives:
gives:

Integrate by parts and discard the total integral. Then divide out by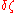 to get:
to get:
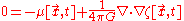
and thus
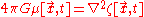
which yields Gauss's law for gravity.
 are replaced by terms involving a continuous charge density
are replaced by terms involving a continuous charge density 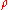 coulombs per cubic meter and current density
coulombs per cubic meter and current density 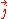 amperes per square meter. The resulting Lagrangian for the electromagnetic field is:
amperes per square meter. The resulting Lagrangian for the electromagnetic field is:
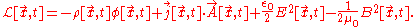
Varying this with respect to , we get
, we get
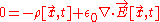
which yields Gauss' law.
Varying instead with respect to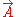 , we get
, we get
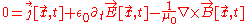
which yields Ampère's law
.
. The Lagrangian of the electromagnetic field is:
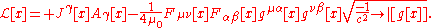
If the four space-time coordinates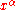 are given in arbitrary units, then:
are given in arbitrary units, then: 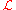 joule seconds is the Lagrangian, a scalar density;
joule seconds is the Lagrangian, a scalar density; 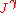 coulombs is the current, a vector density; and
coulombs is the current, a vector density; and 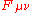 volt seconds is the electromagnetic tensor
volt seconds is the electromagnetic tensor
, a covariant antisymmetric tensor of rank two. Notice that the determinant under the square root sign is applied to the matrix of components of the covariant metric tensor , and
, and 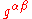 is its inverse. Notice that the units of the Lagrangian changed because we are integrating over
is its inverse. Notice that the units of the Lagrangian changed because we are integrating over 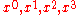 which are unit-less rather than over
which are unit-less rather than over  which have units of seconds meters cubed. The electromagnetic field tensor is formed by anti-symmetrizing the partial derivative of the electromagnetic vector potential; so it is not an independent variable. The square root is needed to convert that term into a scalar density instead of just a scalar, and also to compensate for the change in the units of the variables of integration. The factor of
which have units of seconds meters cubed. The electromagnetic field tensor is formed by anti-symmetrizing the partial derivative of the electromagnetic vector potential; so it is not an independent variable. The square root is needed to convert that term into a scalar density instead of just a scalar, and also to compensate for the change in the units of the variables of integration. The factor of 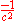 inside the square root is needed to normalize it so that the square root will reduce to one in special relativity (since the determinant is
inside the square root is needed to normalize it so that the square root will reduce to one in special relativity (since the determinant is 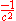 in special relativity).
in special relativity).
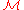 can be written as (using natural units,
can be written as (using natural units, 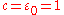 )
)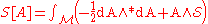
Here, stands for the electromagnetic potential 1-form, and
stands for the electromagnetic potential 1-form, and 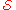 is the current 3-form. Note that Lagrangian is exactly the same thing as in the paragraph above, only that the treatment here is coordinate-free; expanding the integrand into a basis yields the identical, lengthy expression. Expanding the action integral into a basis yields the lengthy Lagrangian expression. Variation of the expression leads to
is the current 3-form. Note that Lagrangian is exactly the same thing as in the paragraph above, only that the treatment here is coordinate-free; expanding the integrand into a basis yields the identical, lengthy expression. Expanding the action integral into a basis yields the lengthy Lagrangian expression. Variation of the expression leads to
These are Maxwell's equations for the electromagnetic potential. Substituting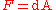 immediately yields the equations for the fields,
immediately yields the equations for the fields,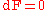

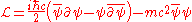
where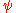 is a Dirac spinor (annihilation operator),
is a Dirac spinor (annihilation operator), 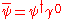 is its Dirac adjoint (creation operator) and
is its Dirac adjoint (creation operator) and  is Feynman notation
is Feynman notation
for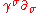 .
.
is:
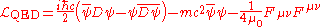
where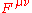 is the electromagnetic tensor
is the electromagnetic tensor
, is the gauge covariant derivative
is the gauge covariant derivative
, and is Feynman notation
is Feynman notation
for .
.
is http://www.fuw.edu.pl/~dobaczew/maub-42w/node9.html http://smallsystems.isn-oldenburg.de/Docs/THEO3/publications/semiclassical.qcd.prep.pdf http://www-zeus.physik.uni-bonn.de/~brock/teaching/jets_ws0405/seminar09/sluka_quark_gluon_jets.pdf:

where is the QCD gauge covariant derivative,
is the QCD gauge covariant derivative,
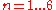 counts the quark types, and
counts the quark types, and 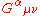 is the gluon field strength
is the gluon field strength
tensor.
, , and a target manifold,
, and a target manifold,  . Let
. Let  be the configuration space of smooth function
be the configuration space of smooth function
s from to
to  .
.
,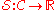 , called the action
, called the action
. Physical reasons determine that it is a mapping
to , not
, not  .
.
In order for the action to be local, we need additional restrictions on the action
. If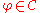 , we assume
, we assume 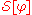 is the integral
is the integral
over of a function of
of a function of  , its derivative
, its derivative
s and the position called the Lagrangian,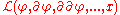 . In other words,
. In other words,

It is assumed below, in addition, that the Lagrangian depends on only the field value and its first derivative but not the higher derivatives.
Given boundary conditions, basically a specification of the value of at the boundary
at the boundary
if is compact
is compact
or some limit on as x approaches
as x approaches  (this will help in doing integration by parts
(this will help in doing integration by parts
), the subspace
of consisting of functions,
consisting of functions,  such that all functional derivative
such that all functional derivative
s of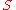 at
at  are zero and
are zero and  satisfies the given boundary conditions is the subspace of on shell solutions.
satisfies the given boundary conditions is the subspace of on shell solutions.
The solution is given by the Euler–Lagrange equations (thanks to the boundary conditions),
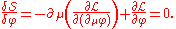
The left hand side is the functional derivative
of the action
with respect to .
.
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
by Irish mathematician William Rowan Hamilton
William Rowan Hamilton
Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
known as Lagrangian mechanics
Lagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
. In classical mechanics, the Lagrangian is defined as the kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
,
 , of the system minus its potential energy
, of the system minus its potential energyPotential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
,
 . In symbols,
. In symbols,
Under conditions that are given in Lagrangian mechanics
Lagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
, if the Lagrangian of a system is known, then the equations of motion
Equation of motion
Equations of motion are equations that describe the behavior of a system in terms of its motion as a function of time...
of the system may be obtained by a direct substitution of the expression for the Lagrangian into the Euler–Lagrange equation, a particular family of partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s.
Importance
The Lagrangian formulation of mechanics is important not just for its broad applications, but also for its role in advancing deep understanding of physicsPhysics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
. Although Lagrange only sought to describe classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, the action principle that is used to derive the Lagrange equation was later recognized to be applicable to quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
as well.
Physical action
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
and quantum-mechanical phase
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
are related via Planck's constant, and the principle of stationary action can be understood in terms of constructive interference of wave functions.
The same principle, and the Lagrangian formalism, are tied closely to Noether's theorem
Noether's theorem
Noether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...
, which connect physical conserved quantities
Conserved quantity
In mathematics, a conserved quantity of a dynamical system is a function H of the dependent variables that is a constant along each trajectory of the system. A conserved quantity can be a useful tool for qualitative analysis...
to continuous symmetries
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
of a physical system.
Lagrangian mechanics and Noether's theorem
Noether's theorem
Noether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...
together yield a natural formalism for first quantization
First quantization
A first quantization of a physical system is a semi-classical treatment of quantum mechanics, in which particles or physical objects are treated using quantum wave functions but the surrounding environment is treated classically...
by including commutators between certain terms of the Lagrangian equations of motion for a physical system.
Advantages over other methods
- The formulation is not tied to any one coordinate system—rather, any convenient variables
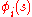 may be used to describe the system; these variables are called "generalized coordinatesGeneralized coordinatesIn the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
may be used to describe the system; these variables are called "generalized coordinatesGeneralized coordinatesIn the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
" and may be any independent variable of the system (for example, strength of the magnetic fieldMagnetic fieldA magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
at a particular location; angleAngleIn geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
of a pulley; position of a particle in space; or degree of excitation of a particular eigenmode in a complex system). This makes it easy to incorporate constraints into a theory by defining coordinates which only describe states of the system which satisfy the constraints.
- If the Lagrangian is invariant under a symmetry, then the resulting equations of motion are also invariant under that symmetry. This is very helpful in showing that theories are consistent with either special relativity or general relativity.
- Equations derived from a Lagrangian will almost automatically be unambiguous and consistent, unlike equations brought together from multiple formulations.
"Cyclic coordinates" and conservation laws
An important property of the Lagrangian is that conservation laws can easily be read off from it. For example, if the Lagrangian
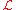 depends on the time-derivative
depends on the time-derivative 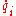 of a generalized coordinate, but not on
of a generalized coordinate, but not on 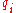 itself, then the generalized momentum,
itself, then the generalized momentum,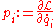 ,
,is a conserved quantity. This is a special case of Noether's theorem
Noether's theorem
Noether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...
. Such coordinates are called "cyclic".
For example, the conservation of the generalized momentum,
-
 ,
,
say, can be directly seen if the Lagrangian of the system is of the form
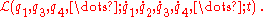
Also, if the time, t, does not appear in
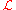 , then the conservation of the Hamiltonian
, then the conservation of the HamiltonianHamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
follows. This is the energy conservation unless the potential energy depends on velocity, as in electrodynamics. More details can be found in any textbook on theoretical mechanics.
Explanation
The equations of motionEquation of motion
Equations of motion are equations that describe the behavior of a system in terms of its motion as a function of time...
are obtained by means of an action
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
principle, written as:

where the action,
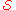 , is a functional
, is a functionalFunctional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
of the dependent variables
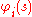 with their derivatives and s itself
with their derivatives and s itself
and where
 denotes the set of n independent variable
denotes the set of n independent variableIndependent variable
The terms "dependent variable" and "independent variable" are used in similar but subtly different ways in mathematics and statistics as part of the standard terminology in those subjects...
s of the system, indexed by
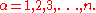
The equations of motion obtained from this functional derivative
Functional derivative
In mathematics and theoretical physics, the functional derivative is a generalization of the gradient. While the latter differentiates with respect to a vector with discrete components, the former differentiates with respect to a continuous function. Both of these can be viewed as extensions of...
are the Euler–Lagrange equations of this action. For example, in the classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
of particles, the only independent variable is time, t. So the Euler-Lagrange equations are

Dynamical systems whose equations of motion are obtainable by means of an action principle on a suitably chosen Lagrangian are known as Lagrangian dynamical systems. Examples of Lagrangian dynamical systems range from the classical version of the Standard Model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
, to Newton's equations, to purely mathematical problems such as geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
equations and Plateau's problem
Plateau's problem
In mathematics, Plateau's problem is to show the existence of a minimal surface with a given boundary, a problem raised by Joseph-Louis Lagrange in 1760. However, it is named after Joseph Plateau who was interested in soap films. The problem is considered part of the calculus of variations...
.
In the rectangular coordinate system
Suppose we have a three-dimensional spaceThree-dimensional space
Three-dimensional space is a geometric 3-parameters model of the physical universe in which we live. These three dimensions are commonly called length, width, and depth , although any three directions can be chosen, provided that they do not lie in the same plane.In physics and mathematics, a...
and the Lagrangian
 .
.Then, the Euler–Lagrange equation is:

where
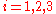 .
.The derivation yields:
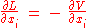

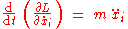
The Euler–Lagrange equations can therefore be written as:

where the time derivative is written conventionally as a dot above the quantity being differentiated, and
 is the del operator
is the del operatorDel
In vector calculus, del is a vector differential operator, usually represented by the nabla symbol \nabla . When applied to a function defined on a one-dimensional domain, it denotes its standard derivative as defined in calculus...
.
Using this result, it can easily be shown that the Lagrangian approach is equivalent to the Newtonian one.
If the force is written in terms of the potential
 ; the resulting equation is
; the resulting equation is  , which is exactly the same equation as in a Newtonian approach for a constant mass object.
, which is exactly the same equation as in a Newtonian approach for a constant mass object.A very similar deduction gives us the expression
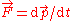 , which is Newton's Second Law in its general form.
, which is Newton's Second Law in its general form.In the spherical coordinate system
Suppose we have a three-dimensional space using spherical coordinates with the Lagrangian
with the Lagrangian
Then the Euler–Lagrange equations are:


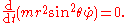
Here the set of parameters
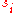 is just the time
is just the time  , and the dynamical variables
, and the dynamical variables  are the trajectories
are the trajectories 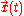 of the particle.
of the particle.Despite the use of standard variables such as
 , the Lagrangian allows the use of any coordinates, which do not need to be orthogonal. These are "generalized coordinates
, the Lagrangian allows the use of any coordinates, which do not need to be orthogonal. These are "generalized coordinatesGeneralized coordinates
In the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
".
Lagrangian of a test particle
A test particle is a particle whose mass and charge are assumed to be so small that its effect on external system is insignificant. It is often a hypothetical simplified point particle with no properties other than mass and charge. Real particles like electrons and up-quarks are more complex and have additional terms in their Lagrangians.Classical test particle with Newtonian gravity
Suppose we are given a particle with mass kilograms, and position
kilograms, and position  meters in a Newtonian gravitation field with potential
meters in a Newtonian gravitation field with potential  joules per kilogram. The particle's world line is parameterized by time
joules per kilogram. The particle's world line is parameterized by time  seconds. The particle's kinetic energy is:
seconds. The particle's kinetic energy is:
and the particle's gravitational potential energy is:
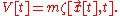
Then its Lagrangian is
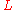 joules where
joules where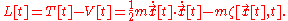
Varying
 in the integral (equivalent to the Euler–Lagrange differential equation), we get
in the integral (equivalent to the Euler–Lagrange differential equation), we get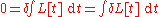

Integrate the first term by parts and discard the total integral. Then divide out the variation to get
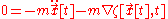
and thus

is the equation of motion — two different expressions for the force.
Special relativistic test particle with electromagnetism
In special relativity, the form of the term which gives rise to the derivative of the momentum must be changed; it is no longer the kinetic energy. It becomes:
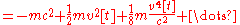
(In special relativity, the energy of a free test particle is
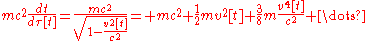 )
)where
 meters per second is the speed of light
meters per second is the speed of lightSpeed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
in vacuum,
 seconds is the proper time (i.e. time measured by a clock moving with the particle) and
seconds is the proper time (i.e. time measured by a clock moving with the particle) and  The second term in the series is just the classical kinetic energy. Suppose the particle has electrical charge
The second term in the series is just the classical kinetic energy. Suppose the particle has electrical charge 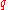 coulombs and is in an electromagnetic field with scalar potential
coulombs and is in an electromagnetic field with scalar potentialScalar potential
A scalar potential is a fundamental concept in vector analysis and physics . The scalar potential is an example of a scalar field...
 volts (a volt is a joule per coulomb) and vector potential
volts (a volt is a joule per coulomb) and vector potentialVector potential
In vector calculus, a vector potential is a vector field whose curl is a given vector field. This is analogous to a scalar potential, which is a scalar field whose negative gradient is a given vector field....
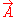 volt seconds per meter. The Lagrangian of a special relativistic test particle in an electromagnetic field is:
volt seconds per meter. The Lagrangian of a special relativistic test particle in an electromagnetic field is: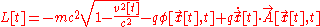
Varying this with respect to
 , we get
, we get
which is

which is the equation for the Lorentz force
Lorentz force
In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
where
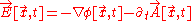

General relativistic test particle
In general relativityGeneral relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, the first term generalizes (includes) both the classical kinetic energy and interaction with the Newtonian gravitational potential. It becomes:

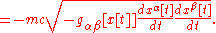
The Lagrangian of a general relativistic test particle in an electromagnetic field is:
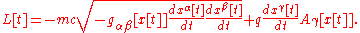
If the four space-time coordinates
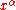 are given in arbitrary units (i.e. unit-less), then
are given in arbitrary units (i.e. unit-less), then  meters squared is the rank 2 symmetric metric tensor
meters squared is the rank 2 symmetric metric tensorMetric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
which is also the gravitational potential. Also,
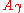 volt seconds is the electromagnetic 4-vector potential. Notice that a factor of c has been absorbed into the square root because it is the equivalent of
volt seconds is the electromagnetic 4-vector potential. Notice that a factor of c has been absorbed into the square root because it is the equivalent of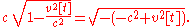
Note that this notion has been directly generalized from special relativity
Lagrangians and Lagrangian densities in field theory
The time integral of the Lagrangian is called the actionAction (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
denoted by
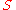 .
.In field theory, a distinction is occasionally made between the Lagrangian
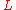 , of which the action is the time integral:
, of which the action is the time integral:
and the Lagrangian density
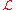 , which one integrates over all space-time to get the action:
, which one integrates over all space-time to get the action: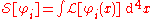
The Lagrangian is then the spatial integral of the Lagrangian density. However,
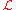 is also frequently simply called the Lagrangian, especially in modern use; it is far more useful in relativistic
is also frequently simply called the Lagrangian, especially in modern use; it is far more useful in relativisticSpecial relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
theories since it is a locally
Principle of locality
In physics, the principle of locality states that an object is influenced directly only by its immediate surroundings. Experiments have shown that quantum mechanically entangled particles must violate either the principle of locality or the form of philosophical realism known as counterfactual...
defined, Lorentz
Lorentz covariance
In standard physics, Lorentz symmetry is "the feature of nature that says experimental results are independent of the orientation or the boost velocity of the laboratory through space"...
scalar
Lorentz scalar
In physics, a Lorentz scalar is a scalar which is invariant under a Lorentz transformation. A Lorentz scalar may be generated from multiplication of vectors or tensors...
field. Both definitions of the Lagrangian can be seen as special cases of the general form, depending on whether the spatial variable
 is incorporated into the index
is incorporated into the index 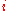 or the parameters
or the parameters  in
in 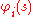 . Quantum field theories
. Quantum field theoriesQuantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
in particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
, such as quantum electrodynamics
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
, are usually described in terms of
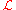 , and the terms in this form of the Lagrangian translate quickly to the rules used in evaluating Feynman diagram
, and the terms in this form of the Lagrangian translate quickly to the rules used in evaluating Feynman diagramFeynman diagram
Feynman diagrams are a pictorial representation scheme for the mathematical expressions governing the behavior of subatomic particles, first developed by the Nobel Prize-winning American physicist Richard Feynman, and first introduced in 1948...
s.
Selected fields
To go with the section on test particles above, here are the equations for the fields in which they move. The equations below pertain to the fields in which the test particles described above move and allow the calculation of those fields. The equations below will not give you the equations of motion of a test particle in the field but will instead give you the potential (field) induced by quantities such as mass or charge density at any point . For example, in the case of Newtonian gravity, the Lagrangian density integrated over space-time gives you an equation which, if solved, would yield
. For example, in the case of Newtonian gravity, the Lagrangian density integrated over space-time gives you an equation which, if solved, would yield 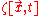 . This
. This 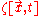 , when substituted back in equation (1), the Lagrangian equation for the test particle in a Newtonian gravitational field, provides the information needed to calculate the acceleration of the particle.
, when substituted back in equation (1), the Lagrangian equation for the test particle in a Newtonian gravitational field, provides the information needed to calculate the acceleration of the particle.Newtonian gravity
The Lagrangian (density) is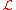 joules per cubic meter. The interaction term
joules per cubic meter. The interaction term 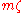 is replaced by a term involving a continuous mass density
is replaced by a term involving a continuous mass density  kilograms per cubic meter. This is necessary because using a point source for a field would result in mathematical difficulties. The resulting Lagrangian for the classical gravitational field is:
kilograms per cubic meter. This is necessary because using a point source for a field would result in mathematical difficulties. The resulting Lagrangian for the classical gravitational field is: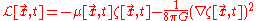
where
 meters cubed per kilogram second squared is the gravitational constant
meters cubed per kilogram second squared is the gravitational constantGravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
. Variation of the integral with respect to
 gives:
gives:
Integrate by parts and discard the total integral. Then divide out by
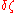 to get:
to get: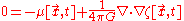
and thus
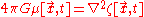
which yields Gauss's law for gravity.
Electromagnetism in special relativity
The interaction terms are replaced by terms involving a continuous charge density
are replaced by terms involving a continuous charge density 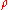 coulombs per cubic meter and current density
coulombs per cubic meter and current density 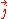 amperes per square meter. The resulting Lagrangian for the electromagnetic field is:
amperes per square meter. The resulting Lagrangian for the electromagnetic field is: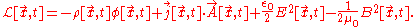
Varying this with respect to
 , we get
, we get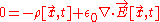
which yields Gauss' law.
Varying instead with respect to
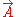 , we get
, we get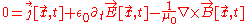
which yields Ampère's law
Ampère's law
In classical electromagnetism, Ampère's circuital law, discovered by André-Marie Ampère in 1826, relates the integrated magnetic field around a closed loop to the electric current passing through the loop...
.
Electromagnetism in general relativity
For the Lagrangian of gravity in general relativity, see Einstein-Hilbert actionEinstein-Hilbert action
The Einstein–Hilbert action in general relativity is the action that yields the Einstein's field equations through the principle of least action...
. The Lagrangian of the electromagnetic field is:
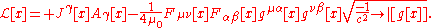
If the four space-time coordinates
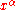 are given in arbitrary units, then:
are given in arbitrary units, then: 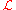 joule seconds is the Lagrangian, a scalar density;
joule seconds is the Lagrangian, a scalar density; 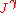 coulombs is the current, a vector density; and
coulombs is the current, a vector density; and 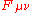 volt seconds is the electromagnetic tensor
volt seconds is the electromagnetic tensorElectromagnetic tensor
The electromagnetic tensor or electromagnetic field tensor is a mathematical object that describes the electromagnetic field of a physical system in Maxwell's theory of electromagnetism...
, a covariant antisymmetric tensor of rank two. Notice that the determinant under the square root sign is applied to the matrix of components of the covariant metric tensor
 , and
, and 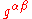 is its inverse. Notice that the units of the Lagrangian changed because we are integrating over
is its inverse. Notice that the units of the Lagrangian changed because we are integrating over 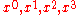 which are unit-less rather than over
which are unit-less rather than over  which have units of seconds meters cubed. The electromagnetic field tensor is formed by anti-symmetrizing the partial derivative of the electromagnetic vector potential; so it is not an independent variable. The square root is needed to convert that term into a scalar density instead of just a scalar, and also to compensate for the change in the units of the variables of integration. The factor of
which have units of seconds meters cubed. The electromagnetic field tensor is formed by anti-symmetrizing the partial derivative of the electromagnetic vector potential; so it is not an independent variable. The square root is needed to convert that term into a scalar density instead of just a scalar, and also to compensate for the change in the units of the variables of integration. The factor of 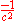 inside the square root is needed to normalize it so that the square root will reduce to one in special relativity (since the determinant is
inside the square root is needed to normalize it so that the square root will reduce to one in special relativity (since the determinant is 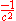 in special relativity).
in special relativity).Electromagnetism using differential forms
Using differential forms, the electromagnetic action in vacuum on a (pseudo-) Riemannian manifold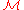 can be written as (using natural units,
can be written as (using natural units, 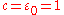 )
)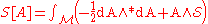
Here,
 stands for the electromagnetic potential 1-form, and
stands for the electromagnetic potential 1-form, and 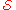 is the current 3-form. Note that Lagrangian is exactly the same thing as in the paragraph above, only that the treatment here is coordinate-free; expanding the integrand into a basis yields the identical, lengthy expression. Expanding the action integral into a basis yields the lengthy Lagrangian expression. Variation of the expression leads to
is the current 3-form. Note that Lagrangian is exactly the same thing as in the paragraph above, only that the treatment here is coordinate-free; expanding the integrand into a basis yields the identical, lengthy expression. Expanding the action integral into a basis yields the lengthy Lagrangian expression. Variation of the expression leads to
These are Maxwell's equations for the electromagnetic potential. Substituting
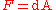 immediately yields the equations for the fields,
immediately yields the equations for the fields,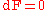

Dirac Lagrangian
The Lagrangian density for a Dirac field is: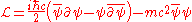
where
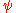 is a Dirac spinor (annihilation operator),
is a Dirac spinor (annihilation operator), 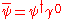 is its Dirac adjoint (creation operator) and
is its Dirac adjoint (creation operator) and  is Feynman notation
is Feynman notationFeynman slash notation
In the study of Dirac fields in quantum field theory, Richard Feynman invented the convenient Feynman slash notation...
for
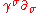 .
.Quantum electrodynamic Lagrangian
The Lagrangian density for QEDQuantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
is:
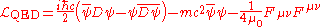
where
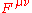 is the electromagnetic tensor
is the electromagnetic tensorElectromagnetic tensor
The electromagnetic tensor or electromagnetic field tensor is a mathematical object that describes the electromagnetic field of a physical system in Maxwell's theory of electromagnetism...
,
 is the gauge covariant derivative
is the gauge covariant derivativeGauge covariant derivative
The gauge covariant derivative is like a generalization of the covariant derivative used in general relativity. If a theory has gauge transformations, it means that some physical properties of certain equations are preserved under those transformations...
, and
 is Feynman notation
is Feynman notationFeynman slash notation
In the study of Dirac fields in quantum field theory, Richard Feynman invented the convenient Feynman slash notation...
for
 .
.Quantum chromodynamic Lagrangian
The Lagrangian density for quantum chromodynamicsQuantum chromodynamics
In theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
is http://www.fuw.edu.pl/~dobaczew/maub-42w/node9.html http://smallsystems.isn-oldenburg.de/Docs/THEO3/publications/semiclassical.qcd.prep.pdf http://www-zeus.physik.uni-bonn.de/~brock/teaching/jets_ws0405/seminar09/sluka_quark_gluon_jets.pdf:

where
 is the QCD gauge covariant derivative,
is the QCD gauge covariant derivative,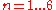 counts the quark types, and
counts the quark types, and 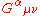 is the gluon field strength
is the gluon field strengthField strength
In physics, the field strength of a field is the magnitude of its vector value.In theoretical physics, field strength is another name for the curvature form...
tensor.
Mathematical formalism
Suppose we have an n-dimensional manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
,
 , and a target manifold,
, and a target manifold,  . Let
. Let  be the configuration space of smooth function
be the configuration space of smooth functionSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s from
 to
to  .
.Examples
- In classical mechanicsClassical mechanicsIn physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
, in the HamiltonianHamiltonian mechanicsHamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
formalism, is the one-dimensional manifold
is the one-dimensional manifold  , representing time and the target space is the cotangent bundleCotangent bundleIn mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
, representing time and the target space is the cotangent bundleCotangent bundleIn mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
of spaceSpaceSpace is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...
of generalized positions. - In field theory,
 is the spacetimeSpacetimeIn physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
is the spacetimeSpacetimeIn physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
manifold and the target space is the set of values the fields can take at any given point. For example, if there are m realReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
-valued scalar fieldScalar fieldIn mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
s, , then the target manifold is
, then the target manifold is 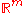 . If the field is a real vector fieldVector fieldIn vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
. If the field is a real vector fieldVector fieldIn vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
, then the target manifold is isomorphic to . There is actually a much more elegant way using tangent bundleTangent bundleIn differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
. There is actually a much more elegant way using tangent bundleTangent bundleIn differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
s over , but we will just stick to this version.
, but we will just stick to this version.
Mathematical development
Consider a functionalFunctional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
,
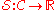 , called the action
, called the actionAction (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
. Physical reasons determine that it is a mapping
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
to
 , not
, not  .
.In order for the action to be local, we need additional restrictions on the action
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
. If
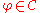 , we assume
, we assume 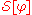 is the integral
is the integralIntegral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
over
 of a function of
of a function of  , its derivative
, its derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s and the position called the Lagrangian,
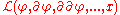 . In other words,
. In other words,
It is assumed below, in addition, that the Lagrangian depends on only the field value and its first derivative but not the higher derivatives.
Given boundary conditions, basically a specification of the value of
 at the boundary
at the boundaryBoundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
if
 is compact
is compactCompact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
or some limit on
 as x approaches
as x approaches  (this will help in doing integration by parts
(this will help in doing integration by partsIntegration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
), the subspace
Subspace topology
In topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
of
 consisting of functions,
consisting of functions,  such that all functional derivative
such that all functional derivativeFunctional derivative
In mathematics and theoretical physics, the functional derivative is a generalization of the gradient. While the latter differentiates with respect to a vector with discrete components, the former differentiates with respect to a continuous function. Both of these can be viewed as extensions of...
s of
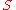 at
at  are zero and
are zero and  satisfies the given boundary conditions is the subspace of on shell solutions.
satisfies the given boundary conditions is the subspace of on shell solutions.The solution is given by the Euler–Lagrange equations (thanks to the boundary conditions),
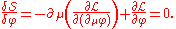
The left hand side is the functional derivative
Functional derivative
In mathematics and theoretical physics, the functional derivative is a generalization of the gradient. While the latter differentiates with respect to a vector with discrete components, the former differentiates with respect to a continuous function. Both of these can be viewed as extensions of...
of the action
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
with respect to
 .
.See also
- Calculus of variationsCalculus of variationsCalculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
- Covariant classical field theoryCovariant classical field theoryIn recent years, there has been renewed interest in covariant classical field theory. Here, classical fields are represented by sections of fiber bundles and their dynamics is phrased in the context of a finite-dimensional space of fields. Nowadays, it is well known that jet bundles and the...
- Functional derivativeFunctional derivativeIn mathematics and theoretical physics, the functional derivative is a generalization of the gradient. While the latter differentiates with respect to a vector with discrete components, the former differentiates with respect to a continuous function. Both of these can be viewed as extensions of...
- Functional integral
- Generalized coordinatesGeneralized coordinatesIn the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
- Hamiltonian mechanicsHamiltonian mechanicsHamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
- Lagrangian and Eulerian coordinatesLagrangian and Eulerian coordinatesIn fluid dynamics and finite-deformation plasticity the Lagrangian specification of the flow field is a way of looking at fluid motion where the observer follows an individual fluid parcel as it moves through space and time. Plotting the position of an individual parcel through time gives the...
- Euler–Lagrange equation
- Lagrangian mechanicsLagrangian mechanicsLagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
- Lagrangian pointLagrangian pointThe Lagrangian points are the five positions in an orbital configuration where a small object affected only by gravity can theoretically be stationary relative to two larger objects...
- Lagrangian systemLagrangian systemIn mathematics, a Lagrangian system is a pair of a smoothfiber bundle Y\to X and a Lagrangian density L which yields the Euler-Lagrange differential operator acting on sections of Y\to X.In classical mechanics, many dynamical systems are...
- Noether's theoremNoether's theoremNoether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...
- Principle of least actionPrinciple of least actionIn physics, the principle of least action – or, more accurately, the principle of stationary action – is a variational principle that, when applied to the action of a mechanical system, can be used to obtain the equations of motion for that system...
- Scalar field theoryScalar field theoryIn theoretical physics, scalar field theory can refer to a classical or quantum theory of scalar fields. A field which is invariant under any Lorentz transformation is called a "scalar", in contrast to a vector or tensor field...
- Einstein-Maxwell-Dirac equationsEinstein-Maxwell-Dirac equationsEinstein-Maxwell-Dirac equations are related to quantum field theory. The current Big Bang Model is a quantum field theory in a curved spacetime. Unfortunately, no such theory is mathematically well-defined; in spite of this, theoreticians claim to extract information from this hypothetical theory...

