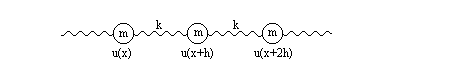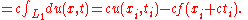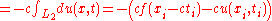Wave equation
Encyclopedia
The wave equation is an important second-order linear partial differential equation
for the description of wave
s – as they occur in physics
– such as sound
waves, light
waves and water
waves. It arises in fields like acoustics
, electromagnetics
, and fluid dynamics
. Historically, the problem of a vibrating string such as that of a musical instrument
was studied by Jean le Rond d'Alembert
, Leonhard Euler
, Daniel Bernoulli
, and Joseph-Louis Lagrange.
s¸ but there are many variations.
In its simplest form, the wave equation concerns a time variable , one or more spatial variables , and a scalar
function , whose values could model the height of a wave. The wave equation for is
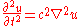
where is the (spatial) Laplacian
is the (spatial) Laplacian
and where c is a fixed constant
.
Solutions of this equation that are initially zero outside some restricted region propagate out from the region at a fixed speed in all spatial directions, as do physical waves from a localized disturbance; the constant c is identified with the propagation speed of the wave. This equation is linear, inasmuch as the sum of any two solutions is again a solution: in physics this property is called the superposition principle
.
The equation alone does not specify a solution; a unique solution is usually obtained by setting a problem with further conditions, such as initial conditions, which prescribe the value and velocity of the wave. Another important class of problems specifies boundary conditions, for which the solutions represent standing waves, or harmonics, analogous to the harmonics of musical instruments.
To model dispersive
wave phenomena, those in which the speed of wave propagation varies with the frequency of the wave, the constant c is replaced by the phase velocity
:
Phenomena in which the speed depends on the amplitude of the wave are modelled by nonlinear wave equations: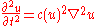
A wave may be superimposed onto another movement (for instance sound propagation in a moving medium like a gas flow). In that case the scalar u will contain a Mach factor
(which is positive for the wave moving along the flow and negative for the reflected wave).
The elastic wave equation in three dimensions describes the propagation of waves in an isotropic homogeneous elastic medium. Most solid materials are elastic, so this equation describes such phenomena as seismic waves in the Earth
and ultrasonic
waves used to detect flaws in materials. While linear, this equation has a more complex form than the equations given above, as it must account for both longitudinal and transverse motion:

where:
Note that in this equation, both force and displacement are vector quantities. Thus, this equation is sometimes known as the vector wave equation.
Variations of the wave equation are also found in quantum mechanics
, plasma physics and general relativity
.
in the following way: Imagine an array of little weights of mass m interconnected with massless springs of length h . The springs have a spring constant
of k:
Here u(x) measures the distance from the equilibrium of the mass situated at x. The forces exerted on the mass at the location
at the location  are:
are:
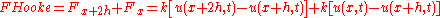
The equation of motion for the weight at the location x+h is given by equating these two forces:
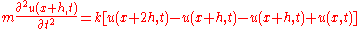
where the time-dependence of u(x) has been made explicit.
If the array of weights consists of N weights spaced evenly over the length L = N h of total mass M = N m, and the total spring constant
of the array K = k/N we can write the above equation as:
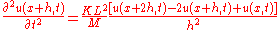
Taking the limit (and assuming smoothness) one gets:
(and assuming smoothness) one gets:
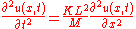
(KL2)/M is the square of the propagation speed in this particular case.
without diffusion,
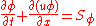 ,
,
we differentiate with respect to to get
to get
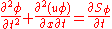 .
.
Assuming that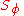 and
and  are constant, we may write
are constant, we may write
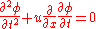 .
.
Substituting for the time derivative of we get
we get
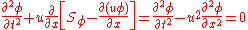 ,
,
where is the speed of propagation of the scalar
is the speed of propagation of the scalar  which, in general, is a function of time and position.
which, in general, is a function of time and position.
in that a relatively simple general solution may be found. Defining new variables:
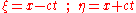
changes the wave equation into
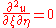
which leads to the general solution

In other words, solutions of the 1D wave equation are sums of a right traveling function and a left traveling function
and a left traveling function  . "Traveling" means that the shape of these individual arbitrary functions with respect to
. "Traveling" means that the shape of these individual arbitrary functions with respect to  stays constant, however the functions are translated left and right with time at the speed
stays constant, however the functions are translated left and right with time at the speed  . This was derived by Jean le Rond d'Alembert
. This was derived by Jean le Rond d'Alembert
.
Another way to arrive at this result is to note that the wave equation may be "factored":
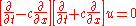

These last two equations are advection equations, one left traveling and one right, both with constant speed .
.
For an initial value problem, the arbitrary functions and
and  can be determined to satisfy initial conditions:
can be determined to satisfy initial conditions:
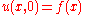
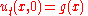
The result is d'Alembert's formula:
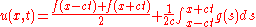
In the classical sense if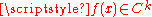 and
and 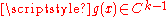 then
then 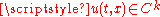 . However, the waveforms F and G may also be generalized functions, such as the delta-function. In that case, the solution may be interpreted as an impulse that travels to the right or the left.
. However, the waveforms F and G may also be generalized functions, such as the delta-function. In that case, the solution may be interpreted as an impulse that travels to the right or the left.
The basic wave equation is a linear differential equation
and so it will adhere to the superposition principle
. This means that the net displacement caused by two or more waves is the sum of the displacements which would have been caused by each wave individually. In addition, the behavior of a wave can be analyzed by breaking up the wave into components, e.g. the Fourier transform
breaks up a wave into sinusoidal components.

This equation may be rewritten as
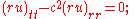
the quantity ru satisfies the one-dimensional wave equation. Therefore there are solutions in the form
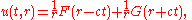
where F and G are arbitrary functions. Each term may be interpreted as a spherical wave that expands or contracts with velocity c. Such waves are generated by a point source
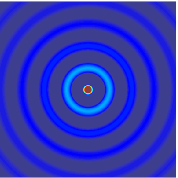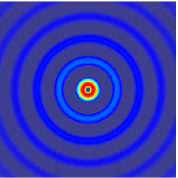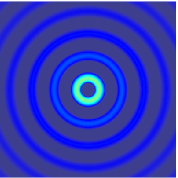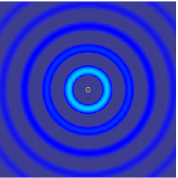
, and they make possible sharp signals whose form is altered only by a decrease in amplitude as r increases (see an illustration of a spherical wave on the top right). Such waves exist only in cases of space with odd dimensions.
 with phase = 0 at
with phase = 0 at  with a peak-to-peak magnitude of
with a peak-to-peak magnitude of 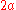 . A spherical wave is propagated from the point. The phase of the propagated wave changes as
. A spherical wave is propagated from the point. The phase of the propagated wave changes as  where
where  is the distance travelled from the source. The magnitude falls off as
is the distance travelled from the source. The magnitude falls off as  since the energy falls off as
since the energy falls off as 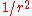 . The complex amplitude of the spherical wave at
. The complex amplitude of the spherical wave at  is therefore given by:
is therefore given by:
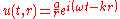
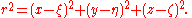
If u is a superposition of such waves with weighting function φ, then

the denominator 4πc is a convenience.
From the definition of the delta-function, u may also be written as
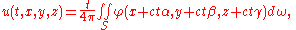
where α, β, and γ are coordinates on the unit sphere S, and ω is the area element on S. This result has the interpretation that u(t,x) is t times the mean value of φ on a sphere of radius ct centered at x:
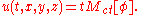
It follows that

The mean value is an even function of t, and hence if
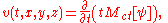
then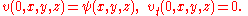
These formulas provide the solution for the initial-value problem for the wave equation. They show that the solution at a given point P, given (t,x,y,z) depends only on the data on the sphere of radius ct that is intersected by the light cone drawn backwards from P. It does not depend upon data on the interior of this sphere. Thus the interior of the sphere is a lacuna
for the solution. This phenomenon is called Huygens' principle. It is true for odd numbers of space dimension, where for one dimension the integration is performed over the boundary of an interval with respect to the Dirac measure. It is not satisfied in even space dimensions. The phenomenon of lacunas has been extensively investigated in Atiyah
, Bott
and Gårding
(1970, 1973).
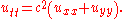
We can use the three-dimensional theory to solve this problem if we regard u as a function in three dimensions that is independent of the third dimension. If

then the three-dimensional solution formula becomes
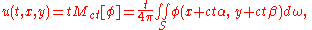
where α and β are the first two coordinates on the unit sphere, and dω is the area element on the sphere. This integral may be rewritten as an integral over the disc D with center (x,y) and radius ct:
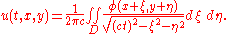
It is apparent that the solution at (t,x,y) depends not only on the data on the light cone where
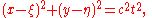
but also on data that are interior to that cone.

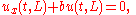
where a and b are non-negative. The case where u is required to vanish at an endpoint is the limit of this condition when the respective a or b approaches infinity. The method of separation of variables
consists in looking for solutions of this problem in the special form
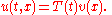
A consequence is that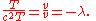
The eigenvalue λ must be determined so that there is a non-trivial solution of the boundary-value problem
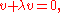
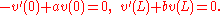
This is a special case of the general problem of Sturm–Liouville theory. If a and b are positive, the eigenvalues are all positive, and the solutions are trigonometric functions. A solution that satisfies square-integrable initial conditions for u and ut can be obtained from expansion of these functions in the appropriate trigonometric series.
If each mass point has the mass , the tension of the string is
, the tension of the string is  , the separation between the mass points is
, the separation between the mass points is 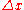 and
and 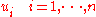 are the offset of these
are the offset of these  points from their equilibrium points (i.e. their position on a straight line between the two attachment points of the string) the vertical component of the force towards point
points from their equilibrium points (i.e. their position on a straight line between the two attachment points of the string) the vertical component of the force towards point  is
is
and the vertical component of the force towards point is
is
Taking the sum of these two forces and dividing with the mass one gets for the vertical motion:
one gets for the vertical motion:
As the mass density is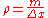
this can be written
The wave equation is obtained by letting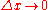 in which case
in which case 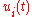 takes the form
takes the form 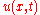 where
where 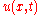 is continuous function of two variables,
is continuous function of two variables, 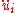 takes the form
takes the form 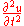 and
and
But the discrete formulation of the equation of state with a finite number of mass point is just the suitable one for a numerical propagation
of the string motion. The boundary condition
where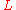 is the length of the string takes in the discrete formulation the form that for the outermost points
is the length of the string takes in the discrete formulation the form that for the outermost points 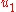 and
and 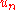 the equation of motion are
the equation of motion are
and
while for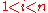
where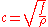
If the string is approximated with 100 discrete mass points one gets the 100 coupled second order differential equations , and or equivalently 200 coupled first order differential equations.
Propagating these up to the times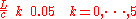
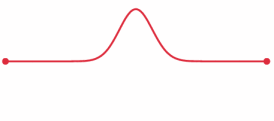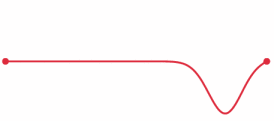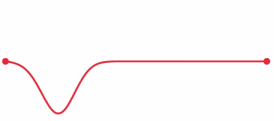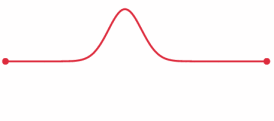
using an 8-th order multistep method the 6 states displayed in figure 2 are found:
The red curve is the initial state at time zero at which the string is "let free" in a predefined shape
with all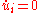 . The blue curve is the state at time
. The blue curve is the state at time 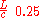 , i.e. after a time that corresponds to the time a wave that is moving with the nominal wave velocity
, i.e. after a time that corresponds to the time a wave that is moving with the nominal wave velocity 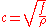 would need for one fourth of the length of the string.
would need for one fourth of the length of the string.
Figure 3 displays the shape of the string at the times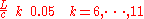 . The wave travels in direction right with the speed
. The wave travels in direction right with the speed 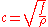 without being actively constraint by the boundary conditions at the two extrems of the string. The shape of the wave is constant, i.e. the curve is indeed of the form
without being actively constraint by the boundary conditions at the two extrems of the string. The shape of the wave is constant, i.e. the curve is indeed of the form
Figure 4 displays the shape of the string at the times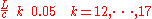 . The constraint on the right extreme starts to interfere with the motion preventing the wave to raise the end of the string.
. The constraint on the right extreme starts to interfere with the motion preventing the wave to raise the end of the string.
Figure 5 displays the shape of the string at the times when the direction of motion is reversed. The red, green and blue curves are the states at the times
when the direction of motion is reversed. The red, green and blue curves are the states at the times 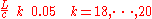 while the 3 black curves correspond to the states at times
while the 3 black curves correspond to the states at times 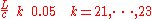 with the wave starting to move back towards left.
with the wave starting to move back towards left.
Figure 6 and figure 7 finally display the shape of the string at the times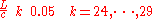 and
and 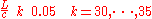 . The wave now travels towards left and the constraints at the end points are not active any more. When finally the other extreme of the string the direction will again be reversed in a way similar to what is displayed in figure 6
. The wave now travels towards left and the constraints at the end points are not active any more. When finally the other extreme of the string the direction will again be reversed in a way similar to what is displayed in figure 6
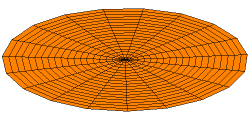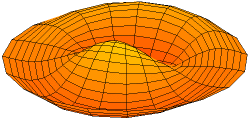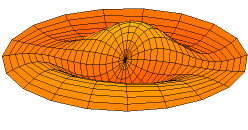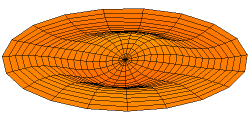 The one-dimensional initial-boundary value theory may be extended to an arbitrary number of space dimensions. Consider a domain D in m-dimensional x space, with boundary B. Then the wave equation is to be satisfied if x is in D and
The one-dimensional initial-boundary value theory may be extended to an arbitrary number of space dimensions. Consider a domain D in m-dimensional x space, with boundary B. Then the wave equation is to be satisfied if x is in D and  . On the boundary of D, the solution u shall satisfy
. On the boundary of D, the solution u shall satisfy

where n is the unit outward normal to B, and a is a non-negative function defined on B. The case where u vanishes on B is a limiting case for a approaching infinity. The initial conditions are

where f and g are defined in D. This problem may be solved by expanding f and g in the eigenfunctions of the Laplacian in D, which satisfy the boundary conditions. Thus the eigenfunction v satisfies

in D, and
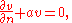
on B.
In the case of two space dimensions, the eigenfunctions may be interpreted as the modes of vibration of a drumhead stretched over the boundary B. If B is a circle, then these eigenfunctions have an angular component that is a trigonometric function of the polar angle θ, multiplied by a Bessel function
(of integer order) of the radial component. Further details are in Helmholtz equation
.
If the boundary is a sphere in three space dimensions, the angular components of the eigenfunctions are spherical harmonics
, and the radial components are Bessel function
s of half-integer order.
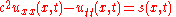
with initial conditions given by


The function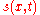 is often called the source function because in practice it describes the effects of the sources of waves on the medium carrying them. Physical examples of source functions include the force driving a wave on a string, or the charge or current density in the Lorenz gauge of electromagnetism
is often called the source function because in practice it describes the effects of the sources of waves on the medium carrying them. Physical examples of source functions include the force driving a wave on a string, or the charge or current density in the Lorenz gauge of electromagnetism
.
One method to solve the initial value problem (with the initial values as posed above) is to take advantage of the property of the wave equation that its solutions obey causality. That is, for any point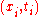 , the value of
, the value of  depends only on the values of
depends only on the values of 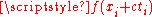 and
and 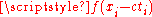 and the values of the function
and the values of the function  between
between  and
and  . This can be seen in d'Alembert's formula, stated above, where these quantities are the only ones that show up in it. Physically, if the maximum propagation speed is
. This can be seen in d'Alembert's formula, stated above, where these quantities are the only ones that show up in it. Physically, if the maximum propagation speed is  , then no part of the wave that can't propagate to a given point by a given time can affect the amplitude at the same point and time.
, then no part of the wave that can't propagate to a given point by a given time can affect the amplitude at the same point and time.
In terms of finding a solution, this causality property means that for any given point on the line being considered, the only area that needs to be considered is the area encompassing all the points that could causally affect the point being considered. Denote the area that casually affects point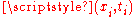 as
as 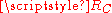 . Suppose we integrate the inhomogeneous wave equation over this region.
. Suppose we integrate the inhomogeneous wave equation over this region.

To simplify this greatly, we can use Green's theorem
to simplify the left side to get the following:
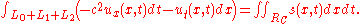
The left side is now the sum of three line integrals along the bounds of the causality region. These turn out to be fairly easy to compute
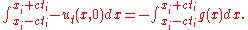
In the above, the term to be integrated with respect to time disappears because the time interval involved is zero, thus .
.
For the other two sides of the region, it is worth noting that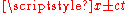 is a constant, namingly
is a constant, namingly 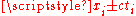 , where the sign is chosen appropriately. Using this, we can get the relation
, where the sign is chosen appropriately. Using this, we can get the relation 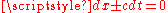 , again choosing the right sign:
, again choosing the right sign:
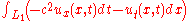
And similarly for the final boundary segment:

Adding the three results together and putting them back in the original integral:

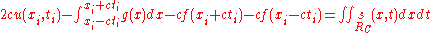
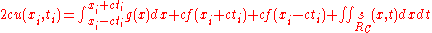

In the last equation of the sequence, the bounds of the integral over the source function have been made explicit. Looking at this solution, which is valid for all choices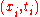 compatible with the wave equation, it is clear that the first two terms are simply d'Alembert's formula, as stated above as the solution of the homogeneous wave equation in one dimension. The difference is in the third term, the integral over the source.
compatible with the wave equation, it is clear that the first two terms are simply d'Alembert's formula, as stated above as the solution of the homogeneous wave equation in one dimension. The difference is in the third term, the integral over the source.
, may be solved by separation of variables, leading to the Mathieu differential equation.
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
for the description of wave
Wave
In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...
s – as they occur in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
– such as sound
Sound
Sound is a mechanical wave that is an oscillation of pressure transmitted through a solid, liquid, or gas, composed of frequencies within the range of hearing and of a level sufficiently strong to be heard, or the sensation stimulated in organs of hearing by such vibrations.-Propagation of...
waves, light
Light
Light or visible light is electromagnetic radiation that is visible to the human eye, and is responsible for the sense of sight. Visible light has wavelength in a range from about 380 nanometres to about 740 nm, with a frequency range of about 405 THz to 790 THz...
waves and water
Water
Water is a chemical substance with the chemical formula H2O. A water molecule contains one oxygen and two hydrogen atoms connected by covalent bonds. Water is a liquid at ambient conditions, but it often co-exists on Earth with its solid state, ice, and gaseous state . Water also exists in a...
waves. It arises in fields like acoustics
Acoustics
Acoustics is the interdisciplinary science that deals with the study of all mechanical waves in gases, liquids, and solids including vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics...
, electromagnetics
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
, and fluid dynamics
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
. Historically, the problem of a vibrating string such as that of a musical instrument
Musical instrument
A musical instrument is a device created or adapted for the purpose of making musical sounds. In principle, any object that produces sound can serve as a musical instrument—it is through purpose that the object becomes a musical instrument. The history of musical instruments dates back to the...
was studied by Jean le Rond d'Alembert
Jean le Rond d'Alembert
Jean-Baptiste le Rond d'Alembert was a French mathematician, mechanician, physicist, philosopher, and music theorist. He was also co-editor with Denis Diderot of the Encyclopédie...
, Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
, Daniel Bernoulli
Daniel Bernoulli
Daniel Bernoulli was a Dutch-Swiss mathematician and was one of the many prominent mathematicians in the Bernoulli family. He is particularly remembered for his applications of mathematics to mechanics, especially fluid mechanics, and for his pioneering work in probability and statistics...
, and Joseph-Louis Lagrange.


Introduction
Wave equations are examples of hyperbolic partial differential equationHyperbolic partial differential equation
In mathematics, a hyperbolic partial differential equation of order n is a partial differential equation that, roughly speaking, has a well-posed initial value problem for the first n−1 derivatives. More precisely, the Cauchy problem can be locally solved for arbitrary initial data along...
s¸ but there are many variations.
In its simplest form, the wave equation concerns a time variable , one or more spatial variables , and a scalar
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
function , whose values could model the height of a wave. The wave equation for is
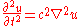
where
 is the (spatial) Laplacian
is the (spatial) LaplacianLaplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
and where c is a fixed constant
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
.
Solutions of this equation that are initially zero outside some restricted region propagate out from the region at a fixed speed in all spatial directions, as do physical waves from a localized disturbance; the constant c is identified with the propagation speed of the wave. This equation is linear, inasmuch as the sum of any two solutions is again a solution: in physics this property is called the superposition principle
Superposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
.
The equation alone does not specify a solution; a unique solution is usually obtained by setting a problem with further conditions, such as initial conditions, which prescribe the value and velocity of the wave. Another important class of problems specifies boundary conditions, for which the solutions represent standing waves, or harmonics, analogous to the harmonics of musical instruments.
To model dispersive
Dispersion (optics)
In optics, dispersion is the phenomenon in which the phase velocity of a wave depends on its frequency, or alternatively when the group velocity depends on the frequency.Media having such a property are termed dispersive media...
wave phenomena, those in which the speed of wave propagation varies with the frequency of the wave, the constant c is replaced by the phase velocity
Phase velocity
The phase velocity of a wave is the rate at which the phase of the wave propagates in space. This is the speed at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave will appear to travel at the phase velocity...
:

Phenomena in which the speed depends on the amplitude of the wave are modelled by nonlinear wave equations:
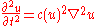
A wave may be superimposed onto another movement (for instance sound propagation in a moving medium like a gas flow). In that case the scalar u will contain a Mach factor
Mach number
Mach number is the speed of an object moving through air, or any other fluid substance, divided by the speed of sound as it is in that substance for its particular physical conditions, including those of temperature and pressure...
(which is positive for the wave moving along the flow and negative for the reflected wave).
The elastic wave equation in three dimensions describes the propagation of waves in an isotropic homogeneous elastic medium. Most solid materials are elastic, so this equation describes such phenomena as seismic waves in the Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
and ultrasonic
Ultrasound
Ultrasound is cyclic sound pressure with a frequency greater than the upper limit of human hearing. Ultrasound is thus not separated from "normal" sound based on differences in physical properties, only the fact that humans cannot hear it. Although this limit varies from person to person, it is...
waves used to detect flaws in materials. While linear, this equation has a more complex form than the equations given above, as it must account for both longitudinal and transverse motion:

where:
 and
and  are the so-called Lamé parameters describing the elastic properties of the medium,
are the so-called Lamé parameters describing the elastic properties of the medium, is the density,
is the density, is the source function (driving force),
is the source function (driving force),- and
 is the displacement vector.
is the displacement vector.
Note that in this equation, both force and displacement are vector quantities. Thus, this equation is sometimes known as the vector wave equation.
Variations of the wave equation are also found in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, plasma physics and general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
.
From Hooke's law
The wave equation in the one dimensional case can be derived from Hooke's lawHooke's law
In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
in the following way: Imagine an array of little weights of mass m interconnected with massless springs of length h . The springs have a spring constant
Stiffness
Stiffness is the resistance of an elastic body to deformation by an applied force along a given degree of freedom when a set of loading points and boundary conditions are prescribed on the elastic body.-Calculations:...
of k:
Here u(x) measures the distance from the equilibrium of the mass situated at x. The forces exerted on the mass
 at the location
at the location  are:
are:
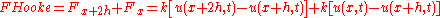
The equation of motion for the weight at the location x+h is given by equating these two forces:
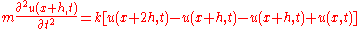
where the time-dependence of u(x) has been made explicit.
If the array of weights consists of N weights spaced evenly over the length L = N h of total mass M = N m, and the total spring constant
Stiffness
Stiffness is the resistance of an elastic body to deformation by an applied force along a given degree of freedom when a set of loading points and boundary conditions are prescribed on the elastic body.-Calculations:...
of the array K = k/N we can write the above equation as:
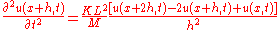
Taking the limit
 (and assuming smoothness) one gets:
(and assuming smoothness) one gets: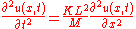
(KL2)/M is the square of the propagation speed in this particular case.
From the generic scalar transport equation
Starting with the generic scalar transport equationGeneric scalar transport equation
The generic scalar transport equation is a general partial differential equation that describes transport phenomena such as heat transfer, mass transfer, fluid dynamics , etc. A general form of the equation is \big...
without diffusion,
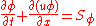 ,
,we differentiate with respect to
 to get
to get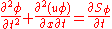 .
.Assuming that
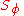 and
and  are constant, we may write
are constant, we may write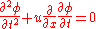 .
.Substituting for the time derivative of
 we get
we get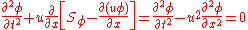 ,
,where
 is the speed of propagation of the scalar
is the speed of propagation of the scalar  which, in general, is a function of time and position.
which, in general, is a function of time and position.General solution
The one dimensional wave equation is unusual for a partial differential equationPartial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
in that a relatively simple general solution may be found. Defining new variables:
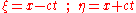
changes the wave equation into
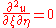
which leads to the general solution

In other words, solutions of the 1D wave equation are sums of a right traveling function
 and a left traveling function
and a left traveling function  . "Traveling" means that the shape of these individual arbitrary functions with respect to
. "Traveling" means that the shape of these individual arbitrary functions with respect to  stays constant, however the functions are translated left and right with time at the speed
stays constant, however the functions are translated left and right with time at the speed  . This was derived by Jean le Rond d'Alembert
. This was derived by Jean le Rond d'AlembertJean le Rond d'Alembert
Jean-Baptiste le Rond d'Alembert was a French mathematician, mechanician, physicist, philosopher, and music theorist. He was also co-editor with Denis Diderot of the Encyclopédie...
.
Another way to arrive at this result is to note that the wave equation may be "factored":
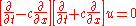

These last two equations are advection equations, one left traveling and one right, both with constant speed
 .
.For an initial value problem, the arbitrary functions
 and
and  can be determined to satisfy initial conditions:
can be determined to satisfy initial conditions: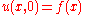
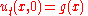
The result is d'Alembert's formula:
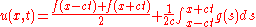
In the classical sense if
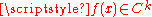 and
and 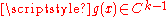 then
then 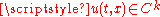 . However, the waveforms F and G may also be generalized functions, such as the delta-function. In that case, the solution may be interpreted as an impulse that travels to the right or the left.
. However, the waveforms F and G may also be generalized functions, such as the delta-function. In that case, the solution may be interpreted as an impulse that travels to the right or the left.The basic wave equation is a linear differential equation
Linear differential equation
Linear differential equations are of the formwhere the differential operator L is a linear operator, y is the unknown function , and the right hand side ƒ is a given function of the same nature as y...
and so it will adhere to the superposition principle
Superposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
. This means that the net displacement caused by two or more waves is the sum of the displacements which would have been caused by each wave individually. In addition, the behavior of a wave can be analyzed by breaking up the wave into components, e.g. the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
breaks up a wave into sinusoidal components.
Scalar wave equation in three space dimensions
The solution of the initial-value problem for the wave equation in three space dimensions can be obtained from the solution for a spherical wave. This result can then be used to obtain the solution in two space dimensions.Spherical waves
The wave equation is unchanged under rotations of the spatial coordinates, and therefore one may expect to find solutions that depend only on the radial distance from a given point. Such solutions must satisfy
This equation may be rewritten as
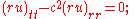
the quantity ru satisfies the one-dimensional wave equation. Therefore there are solutions in the form
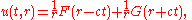
where F and G are arbitrary functions. Each term may be interpreted as a spherical wave that expands or contracts with velocity c. Such waves are generated by a point source
Point source
A point source is a localised, relatively small source of something.Point source may also refer to:*Point source , a localised source of pollution**Point source water pollution, water pollution with a localized source...
, and they make possible sharp signals whose form is altered only by a decrease in amplitude as r increases (see an illustration of a spherical wave on the top right). Such waves exist only in cases of space with odd dimensions.
Monochromatic spherical wave
A point source is vibrating at a single frequencyFrequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
 with phase = 0 at
with phase = 0 at  with a peak-to-peak magnitude of
with a peak-to-peak magnitude of 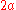 . A spherical wave is propagated from the point. The phase of the propagated wave changes as
. A spherical wave is propagated from the point. The phase of the propagated wave changes as  where
where  is the distance travelled from the source. The magnitude falls off as
is the distance travelled from the source. The magnitude falls off as  since the energy falls off as
since the energy falls off as 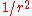 . The complex amplitude of the spherical wave at
. The complex amplitude of the spherical wave at  is therefore given by:
is therefore given by: 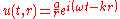
Solution of a general initial-value problem
The wave equation is linear in u and it is left unaltered by translations in space and time. Therefore we can generate a great variety of solutions by translating and summing spherical waves. Let φ(ξ,η,ζ) be an arbitrary function of three independent variables, and let the spherical wave form F be a delta-function: that is, let F be a weak limit of continuous functions whose integral is unity, but whose support (the region where the function is non-zero) shrinks to the origin. Let a family of spherical waves have center at (ξ,η,ζ), and let r be the radial distance from that point. Thus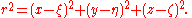
If u is a superposition of such waves with weighting function φ, then

the denominator 4πc is a convenience.
From the definition of the delta-function, u may also be written as
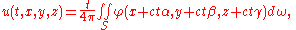
where α, β, and γ are coordinates on the unit sphere S, and ω is the area element on S. This result has the interpretation that u(t,x) is t times the mean value of φ on a sphere of radius ct centered at x:
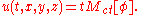
It follows that

The mean value is an even function of t, and hence if
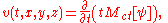
then
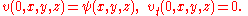
These formulas provide the solution for the initial-value problem for the wave equation. They show that the solution at a given point P, given (t,x,y,z) depends only on the data on the sphere of radius ct that is intersected by the light cone drawn backwards from P. It does not depend upon data on the interior of this sphere. Thus the interior of the sphere is a lacuna
Petrovsky lacuna
In mathematics, a Petrovsky lacuna, named for the Russian mathematician I. G. Petrovsky, is a region where the fundamental solution of a linear hyperbolic partial differential equation vanishes....
for the solution. This phenomenon is called Huygens' principle. It is true for odd numbers of space dimension, where for one dimension the integration is performed over the boundary of an interval with respect to the Dirac measure. It is not satisfied in even space dimensions. The phenomenon of lacunas has been extensively investigated in Atiyah
Michael Atiyah
Sir Michael Francis Atiyah, OM, FRS, FRSE is a British mathematician working in geometry.Atiyah grew up in Sudan and Egypt but spent most of his academic life in the United Kingdom at Oxford and Cambridge, and in the United States at the Institute for Advanced Study...
, Bott
Raoul Bott
Raoul Bott, FRS was a Hungarian mathematician known for numerous basic contributions to geometry in its broad sense...
and Gårding
Lars Gårding
Lars Gårding is a Swedish mathematician. He has made notable contributions to the study of partial differential operators. He is a professor emeritus of mathematics at Lund University in Sweden...
(1970, 1973).
Scalar wave equation in two space dimensions
In two space dimensions, the wave equation is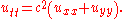
We can use the three-dimensional theory to solve this problem if we regard u as a function in three dimensions that is independent of the third dimension. If

then the three-dimensional solution formula becomes
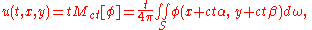
where α and β are the first two coordinates on the unit sphere, and dω is the area element on the sphere. This integral may be rewritten as an integral over the disc D with center (x,y) and radius ct:
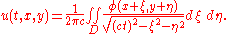
It is apparent that the solution at (t,x,y) depends not only on the data on the light cone where
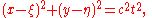
but also on data that are interior to that cone.
The Sturm-Liouville formulation
A flexible string that is stretched between two points x = 0 and x = L satisfies the wave equation for t > 0 and 0 < x < L. On the boundary points, u may satisfy a variety of boundary conditions. A general form that is appropriate for applications is
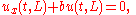
where a and b are non-negative. The case where u is required to vanish at an endpoint is the limit of this condition when the respective a or b approaches infinity. The method of separation of variables
Separation of variables
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
consists in looking for solutions of this problem in the special form
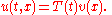
A consequence is that
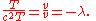
The eigenvalue λ must be determined so that there is a non-trivial solution of the boundary-value problem
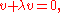
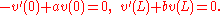
This is a special case of the general problem of Sturm–Liouville theory. If a and b are positive, the eigenvalues are all positive, and the solutions are trigonometric functions. A solution that satisfies square-integrable initial conditions for u and ut can be obtained from expansion of these functions in the appropriate trigonometric series.
Investigation by numerical methods
Approximating the continuous string with a finite number of equidistant mass points one gets the following physical model:If each mass point has the mass
 , the tension of the string is
, the tension of the string is  , the separation between the mass points is
, the separation between the mass points is 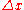 and
and 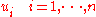 are the offset of these
are the offset of these  points from their equilibrium points (i.e. their position on a straight line between the two attachment points of the string) the vertical component of the force towards point
points from their equilibrium points (i.e. their position on a straight line between the two attachment points of the string) the vertical component of the force towards point  is
is
and the vertical component of the force towards point
 is
is
Taking the sum of these two forces and dividing with the mass
 one gets for the vertical motion:
one gets for the vertical motion:
As the mass density is
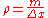
this can be written
The wave equation is obtained by letting
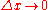 in which case
in which case 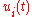 takes the form
takes the form 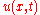 where
where 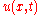 is continuous function of two variables,
is continuous function of two variables, 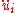 takes the form
takes the form 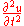 and
and
But the discrete formulation of the equation of state with a finite number of mass point is just the suitable one for a numerical propagation
Numerical ordinary differential equations
Numerical ordinary differential equations is the part of numerical analysis which studies the numerical solution of ordinary differential equations...
of the string motion. The boundary condition

where
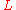 is the length of the string takes in the discrete formulation the form that for the outermost points
is the length of the string takes in the discrete formulation the form that for the outermost points 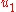 and
and 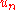 the equation of motion are
the equation of motion are
and
while for
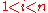
where
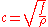
If the string is approximated with 100 discrete mass points one gets the 100 coupled second order differential equations , and or equivalently 200 coupled first order differential equations.
Propagating these up to the times
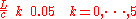
using an 8-th order multistep method the 6 states displayed in figure 2 are found:
The red curve is the initial state at time zero at which the string is "let free" in a predefined shape
with all
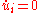 . The blue curve is the state at time
. The blue curve is the state at time 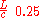 , i.e. after a time that corresponds to the time a wave that is moving with the nominal wave velocity
, i.e. after a time that corresponds to the time a wave that is moving with the nominal wave velocity 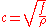 would need for one fourth of the length of the string.
would need for one fourth of the length of the string.Figure 3 displays the shape of the string at the times
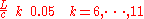 . The wave travels in direction right with the speed
. The wave travels in direction right with the speed 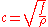 without being actively constraint by the boundary conditions at the two extrems of the string. The shape of the wave is constant, i.e. the curve is indeed of the form
without being actively constraint by the boundary conditions at the two extrems of the string. The shape of the wave is constant, i.e. the curve is indeed of the form
Figure 4 displays the shape of the string at the times
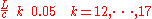 . The constraint on the right extreme starts to interfere with the motion preventing the wave to raise the end of the string.
. The constraint on the right extreme starts to interfere with the motion preventing the wave to raise the end of the string.Figure 5 displays the shape of the string at the times
 when the direction of motion is reversed. The red, green and blue curves are the states at the times
when the direction of motion is reversed. The red, green and blue curves are the states at the times 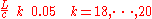 while the 3 black curves correspond to the states at times
while the 3 black curves correspond to the states at times 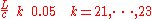 with the wave starting to move back towards left.
with the wave starting to move back towards left.Figure 6 and figure 7 finally display the shape of the string at the times
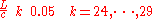 and
and 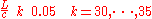 . The wave now travels towards left and the constraints at the end points are not active any more. When finally the other extreme of the string the direction will again be reversed in a way similar to what is displayed in figure 6
. The wave now travels towards left and the constraints at the end points are not active any more. When finally the other extreme of the string the direction will again be reversed in a way similar to what is displayed in figure 6Several space dimensions

 . On the boundary of D, the solution u shall satisfy
. On the boundary of D, the solution u shall satisfy
where n is the unit outward normal to B, and a is a non-negative function defined on B. The case where u vanishes on B is a limiting case for a approaching infinity. The initial conditions are

where f and g are defined in D. This problem may be solved by expanding f and g in the eigenfunctions of the Laplacian in D, which satisfy the boundary conditions. Thus the eigenfunction v satisfies

in D, and
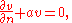
on B.
In the case of two space dimensions, the eigenfunctions may be interpreted as the modes of vibration of a drumhead stretched over the boundary B. If B is a circle, then these eigenfunctions have an angular component that is a trigonometric function of the polar angle θ, multiplied by a Bessel function
Bessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
(of integer order) of the radial component. Further details are in Helmholtz equation
Helmholtz equation
The Helmholtz equation, named for Hermann von Helmholtz, is the elliptic partial differential equation\nabla^2 A + k^2 A = 0where ∇2 is the Laplacian, k is the wavenumber, and A is the amplitude.-Motivation and uses:...
.
If the boundary is a sphere in three space dimensions, the angular components of the eigenfunctions are spherical harmonics
Spherical harmonics
In mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...
, and the radial components are Bessel function
Bessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
s of half-integer order.
Inhomogeneous wave equation in one dimension
The inhomogeneous wave equation in one dimension is the following: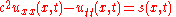
with initial conditions given by


The function
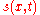 is often called the source function because in practice it describes the effects of the sources of waves on the medium carrying them. Physical examples of source functions include the force driving a wave on a string, or the charge or current density in the Lorenz gauge of electromagnetism
is often called the source function because in practice it describes the effects of the sources of waves on the medium carrying them. Physical examples of source functions include the force driving a wave on a string, or the charge or current density in the Lorenz gauge of electromagnetismElectromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
.
One method to solve the initial value problem (with the initial values as posed above) is to take advantage of the property of the wave equation that its solutions obey causality. That is, for any point
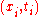 , the value of
, the value of  depends only on the values of
depends only on the values of 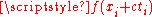 and
and 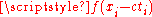 and the values of the function
and the values of the function  between
between  and
and  . This can be seen in d'Alembert's formula, stated above, where these quantities are the only ones that show up in it. Physically, if the maximum propagation speed is
. This can be seen in d'Alembert's formula, stated above, where these quantities are the only ones that show up in it. Physically, if the maximum propagation speed is  , then no part of the wave that can't propagate to a given point by a given time can affect the amplitude at the same point and time.
, then no part of the wave that can't propagate to a given point by a given time can affect the amplitude at the same point and time.In terms of finding a solution, this causality property means that for any given point on the line being considered, the only area that needs to be considered is the area encompassing all the points that could causally affect the point being considered. Denote the area that casually affects point
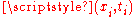 as
as 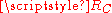 . Suppose we integrate the inhomogeneous wave equation over this region.
. Suppose we integrate the inhomogeneous wave equation over this region.
To simplify this greatly, we can use Green's theorem
Green's theorem
In mathematics, Green's theorem gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C...
to simplify the left side to get the following:
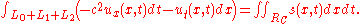
The left side is now the sum of three line integrals along the bounds of the causality region. These turn out to be fairly easy to compute
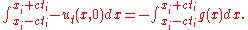
In the above, the term to be integrated with respect to time disappears because the time interval involved is zero, thus
 .
.For the other two sides of the region, it is worth noting that
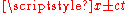 is a constant, namingly
is a constant, namingly 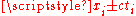 , where the sign is chosen appropriately. Using this, we can get the relation
, where the sign is chosen appropriately. Using this, we can get the relation 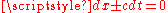 , again choosing the right sign:
, again choosing the right sign: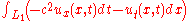
And similarly for the final boundary segment:

Adding the three results together and putting them back in the original integral:

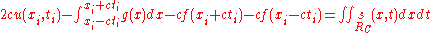
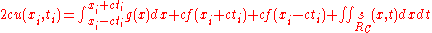

In the last equation of the sequence, the bounds of the integral over the source function have been made explicit. Looking at this solution, which is valid for all choices
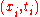 compatible with the wave equation, it is clear that the first two terms are simply d'Alembert's formula, as stated above as the solution of the homogeneous wave equation in one dimension. The difference is in the third term, the integral over the source.
compatible with the wave equation, it is clear that the first two terms are simply d'Alembert's formula, as stated above as the solution of the homogeneous wave equation in one dimension. The difference is in the third term, the integral over the source.Other coordinate systems
In three dimensions, the wave equation, when written in elliptic cylindrical coordinatesElliptic cylindrical coordinates
Elliptic cylindrical coordinates are a three-dimensional orthogonal coordinate system that results from projecting the two-dimensional elliptic coordinate system in the...
, may be solved by separation of variables, leading to the Mathieu differential equation.
See also
- Acoustic wave equationAcoustic wave equationIn physics, the acoustic wave equation governs the propagation of acoustic waves through a material medium. The form of the equation is a second order partial differential equation. The equation describes the evolution of acoustic pressure p or particle velocity u as a function of position r and...
- Electromagnetic wave equationElectromagnetic wave equationThe electromagnetic wave equation is a second-order partial differential equation that describes the propagation of electromagnetic waves through a medium or in a vacuum...
- Helmholtz equationHelmholtz equationThe Helmholtz equation, named for Hermann von Helmholtz, is the elliptic partial differential equation\nabla^2 A + k^2 A = 0where ∇2 is the Laplacian, k is the wavenumber, and A is the amplitude.-Motivation and uses:...
- Inhomogeneous electromagnetic wave equationInhomogeneous electromagnetic wave equationLocalized time-varying charge and current densities can act as sources of electromagnetic waves in a vacuum. Maxwell's equations can be written in the form of a inhomogeneous electromagnetic wave equation with sources...
- Laplace operatorLaplace operatorIn mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
- Schrödinger equationSchrödinger equationThe Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
- Standing waveStanding waveIn physics, a standing wave – also known as a stationary wave – is a wave that remains in a constant position.This phenomenon can occur because the medium is moving in the opposite direction to the wave, or it can arise in a stationary medium as a result of interference between two waves traveling...
- Vibrations of a circular drumVibrations of a circular drumThe vibrations of an idealized circular drum, essentially an elastic membrane of uniform thickness attached to a rigid circular frame, are solutions of the wave equation with zero boundary conditions....
- Bateman transformBateman transformIn the mathematical study of partial differential equation, the Bateman transform is a method for solving the Laplace equation in four dimensions and wave equation in three by using a line integral of a holomorphic function in three complex variables...
- Maxwell's equationsMaxwell's equationsMaxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
- Wheeler-Feynman absorber theory
External links
- Nonlinear Wave Equations by Stephen WolframStephen WolframStephen Wolfram is a British scientist and the chief designer of the Mathematica software application and the Wolfram Alpha computational knowledge engine.- Biography :...
and Rob Knapp and Nonlinear Wave Equation Explorer by Stephen WolframStephen WolframStephen Wolfram is a British scientist and the chief designer of the Mathematica software application and the Wolfram Alpha computational knowledge engine.- Biography :...
, and Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
. - Mathematical aspects of wave equations are discussed on the Dispersive PDE Wiki.