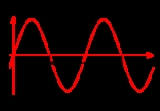
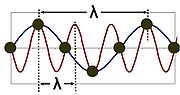
Wavelength
Encyclopedia
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
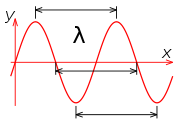
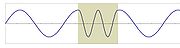
, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.
It is usually determined by considering the distance between consecutive corresponding points of the same phase
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
, such as crests, troughs, or zero crossing
Zero crossing
Zero-crossing is a commonly used term in electronics, mathematics, and image processing. In mathematical terms, a "zero-crossing" is a point where the sign of a function changes Zero-crossing is a commonly used term in electronics, mathematics, and image processing. In mathematical terms, a...
s, and is a characteristic of both traveling waves and standing wave
Standing wave
In physics, a standing wave – also known as a stationary wave – is a wave that remains in a constant position.This phenomenon can occur because the medium is moving in the opposite direction to the wave, or it can arise in a stationary medium as a result of interference between two waves traveling...
s, as well as other spatial wave patterns. Wavelength is commonly designated by the Greek letter lambda
Lambda
Lambda is the 11th letter of the Greek alphabet. In the system of Greek numerals lambda has a value of 30. Lambda is related to the Phoenician letter Lamed . Letters in other alphabets that stemmed from lambda include the Roman L and the Cyrillic letter El...
(λ). The concept can also be applied to periodic waves of non-sinusoidal shape.
The term wavelength is also sometimes applied to modulated
Modulation
In electronics and telecommunications, modulation is the process of varying one or more properties of a high-frequency periodic waveform, called the carrier signal, with a modulating signal which typically contains information to be transmitted...
waves, and to the sinusoidal envelopes
Envelope (mathematics)
In geometry, an envelope of a family of curves in the plane is a curve that is tangent to each member of the family at some point. Classically, a point on the envelope can be thought of as the intersection of two "adjacent" curves, meaning the limit of intersections of nearby curves...
of modulated waves or waves formed by interference of several sinusoids. The SI
Si
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
unit of wavelength is the meter.
Assuming a sinusoidal wave moving at a fixed wave speed, wavelength is inversely proportional to frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
: waves with higher frequencies have shorter wavelengths, and lower frequencies have longer wavelengths.
Examples of wave-like phenomena are sound waves, light
Light
Light or visible light is electromagnetic radiation that is visible to the human eye, and is responsible for the sense of sight. Visible light has wavelength in a range from about 380 nanometres to about 740 nm, with a frequency range of about 405 THz to 790 THz...
, and water waves. A sound
Sound
Sound is a mechanical wave that is an oscillation of pressure transmitted through a solid, liquid, or gas, composed of frequencies within the range of hearing and of a level sufficiently strong to be heard, or the sensation stimulated in organs of hearing by such vibrations.-Propagation of...
wave is a periodic variation in air pressure
Sound pressure
Sound pressure or acoustic pressure is the local pressure deviation from the ambient atmospheric pressure caused by a sound wave. Sound pressure can be measured using a microphone in air and a hydrophone in water...
, while in light
Light
Light or visible light is electromagnetic radiation that is visible to the human eye, and is responsible for the sense of sight. Visible light has wavelength in a range from about 380 nanometres to about 740 nm, with a frequency range of about 405 THz to 790 THz...
and other electromagnetic radiation
Electromagnetic radiation
Electromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
the strength of the electric
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
and the magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
vary. Water waves are periodic variations in the height of a body of water. In a crystal lattice vibration, atomic positions vary periodically in both lattice position and time.
Wavelength is a measure of the distance between repetitions of a shape feature such as peaks, valleys, or zero-crossings, not a measure of how far any given particle moves. For example, in waves over deep water a particle in the water moves in a circle of the same diameter as the wave height, unrelated to wavelength.
Sinusoidal waves
In linearLinear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
media, any wave pattern can be described in terms of the independent propagation of sinusoidal components.
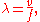
where v is called the phase speed (magnitude of the phase velocity
Phase velocity
The phase velocity of a wave is the rate at which the phase of the wave propagates in space. This is the speed at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave will appear to travel at the phase velocity...
) of the wave and f is the wave's frequency.
In the case of electromagnetic radiation
Electromagnetic radiation
Electromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
—such as light—in free space, the phase speed is the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
, about 3×108
Scientific notation
Scientific notation is a way of writing numbers that are too large or too small to be conveniently written in standard decimal notation. Scientific notation has a number of useful properties and is commonly used in calculators and by scientists, mathematicians, doctors, and engineers.In scientific...
m/s. Thus the wavelength of a 100 MHz electromagnetic (radio) wave is about: 3×108 m/s divided by 108 Hz = 3 metres. Visible light ranges from deep red
Red
Red is any of a number of similar colors evoked by light consisting predominantly of the longest wavelengths of light discernible by the human eye, in the wavelength range of roughly 630–740 nm. Longer wavelengths than this are called infrared , and cannot be seen by the naked eye...
, roughly 700 nm
Nanometre
A nanometre is a unit of length in the metric system, equal to one billionth of a metre. The name combines the SI prefix nano- with the parent unit name metre .The nanometre is often used to express dimensions on the atomic scale: the diameter...
, to violet
Violet (color)
As the name of a color, violet is synonymous with a bluish purple, when the word "purple" is used in the common English language sense of any color between blue and red, not including either blue or red...
, roughly 400 nm (430–750 THz) (for other examples, see electromagnetic spectrum
Electromagnetic spectrum
The electromagnetic spectrum is the range of all possible frequencies of electromagnetic radiation. The "electromagnetic spectrum" of an object is the characteristic distribution of electromagnetic radiation emitted or absorbed by that particular object....
).
For sound waves in air, the speed of sound
Speed of sound
The speed of sound is the distance travelled during a unit of time by a sound wave propagating through an elastic medium. In dry air at , the speed of sound is . This is , or about one kilometer in three seconds or approximately one mile in five seconds....
is 343 m/s (1238 km/h) (at room temperature and atmospheric pressure
Standard conditions for temperature and pressure
Standard condition for temperature and pressure are standard sets of conditions for experimental measurements established to allow comparisons to be made between different sets of data...
). The wavelengths of sound frequencies audible to the human ear (20 Hz
Hertz
The hertz is the SI unit of frequency defined as the number of cycles per second of a periodic phenomenon. One of its most common uses is the description of the sine wave, particularly those used in radio and audio applications....
–20 kHz) are between approximately 17 m
Metre
The metre , symbol m, is the base unit of length in the International System of Units . Originally intended to be one ten-millionth of the distance from the Earth's equator to the North Pole , its definition has been periodically refined to reflect growing knowledge of metrology...
and 17 mm
Millimetre
The millimetre is a unit of length in the metric system, equal to one thousandth of a metre, which is the SI base unit of length....
, respectively, assuming a typical speed of sound
Speed of sound
The speed of sound is the distance travelled during a unit of time by a sound wave propagating through an elastic medium. In dry air at , the speed of sound is . This is , or about one kilometer in three seconds or approximately one mile in five seconds....
of about 343 m/s. Note that the wavelengths in audible sound are much longer than those in visible light.
Frequency and wavelength can change independently, but only when the speed of the wave changes. For example, when light enters another medium, its speed and wavelength change while its frequency does not; this change of wavelength causes refraction
Refraction
Refraction is the change in direction of a wave due to a change in its speed. It is essentially a surface phenomenon . The phenomenon is mainly in governance to the law of conservation of energy. The proper explanation would be that due to change of medium, the phase velocity of the wave is changed...
, or a change in propagation direction of waves that encounter the interface between media at an angle.
Standing waves
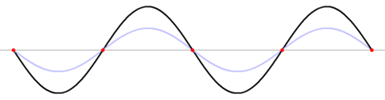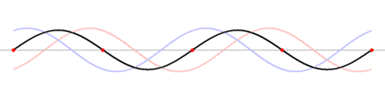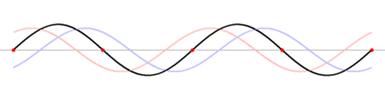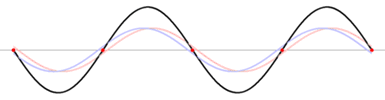
Standing wave
In physics, a standing wave – also known as a stationary wave – is a wave that remains in a constant position.This phenomenon can occur because the medium is moving in the opposite direction to the wave, or it can arise in a stationary medium as a result of interference between two waves traveling...
is an undulatory motion that stays in one place. A sinusoidal standing wave includes stationary points of no motion, called nodes
Node (physics)
A node is a point along a standing wave where the wave has minimal amplitude. For instance, in a vibrating guitar string, the ends of the string are nodes. By changing the position of the end node through frets, the guitarist changes the effective length of the vibrating string and thereby the...
, and the wavelength is twice the distance between nodes. The wavelength, period, and wave velocity are related as before, if the stationary wave is viewed as the sum of two traveling sinusoidal waves of oppositely directed velocities.
Mathematical representation
Traveling sinusoidal waves are often represented mathematically in terms of their velocity v (in the x direction), frequency f and wavelength λ as:
where y is the value of the wave at any position x and time t, and A is the amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
of the wave. They are also commonly expressed in terms of (radian) wavenumber
Wavenumber
In the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
k (
 times the reciprocal of wavelength) and angular frequency
times the reciprocal of wavelength) and angular frequencyAngular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
ω (
 times the frequency) as:
times the frequency) as:
in which wavelength and wavenumber are related to velocity and frequency as:
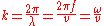
or
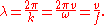
Dispersion relation
In physics and electrical engineering, dispersion most often refers to frequency-dependent effects in wave propagation. Note, however, that there are several other uses of the word "dispersion" in the physical sciences....
. This is not generally a simple inverse relation because the wave velocity itself typically varies with frequency.
Wave vector
In physics, a wave vector is a vector which helps describe a wave. Like any vector, it has a magnitude and direction, both of which are important: Its magnitude is either the wavenumber or angular wavenumber of the wave , and its direction is ordinarily the direction of wave propagation In...
that specifies the direction and wavenumber of a plane wave
Plane wave
In the physics of wave propagation, a plane wave is a constant-frequency wave whose wavefronts are infinite parallel planes of constant peak-to-peak amplitude normal to the phase velocity vector....
in 3-space, parameterized by position vector r. In that case, the wavenumber k, the magnitude of k, is still in the same relationship with wavelength as shown above, with v being interpreted as scalar speed in the direction of the wave vector. The first form, using reciprocal wavelength in the phase, does not generalize as easily to a wave in an arbitrary direction.
Generalizations to sinusoids of other phases, and to complex exponentials, are also common; see plane wave
Plane wave
In the physics of wave propagation, a plane wave is a constant-frequency wave whose wavefronts are infinite parallel planes of constant peak-to-peak amplitude normal to the phase velocity vector....
. The typical convention of using the cosine phase instead of the sine
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
phase when describing a wave is based on the fact that the cosine is the real part of the complex exponential in the wave
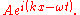
General media
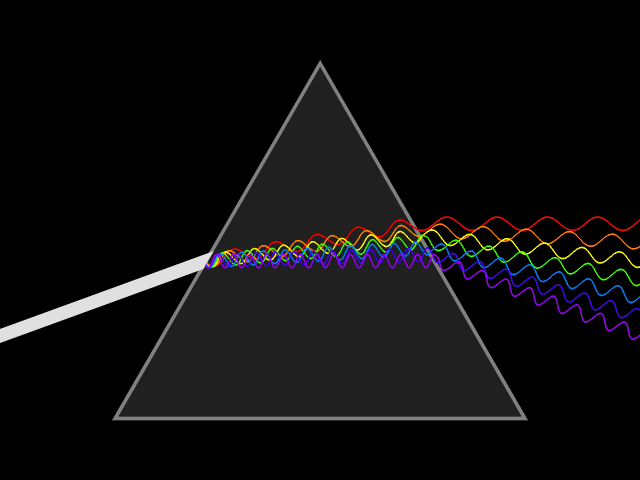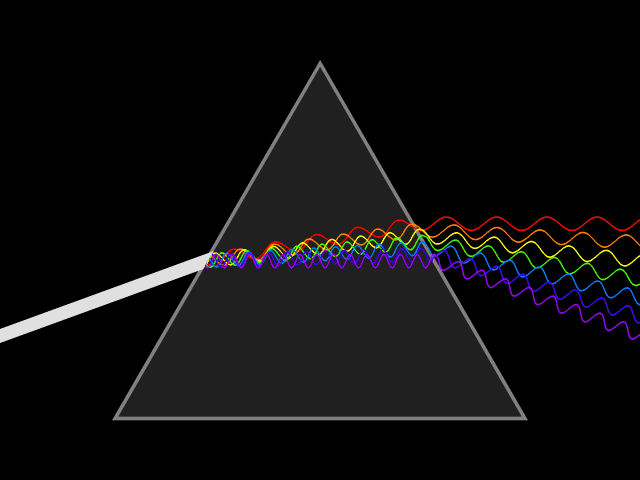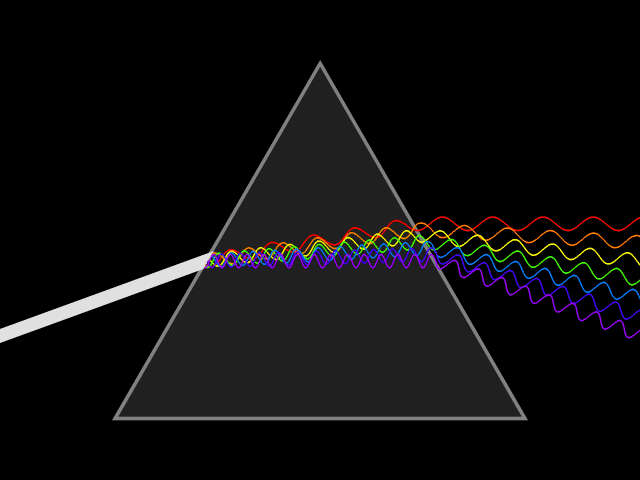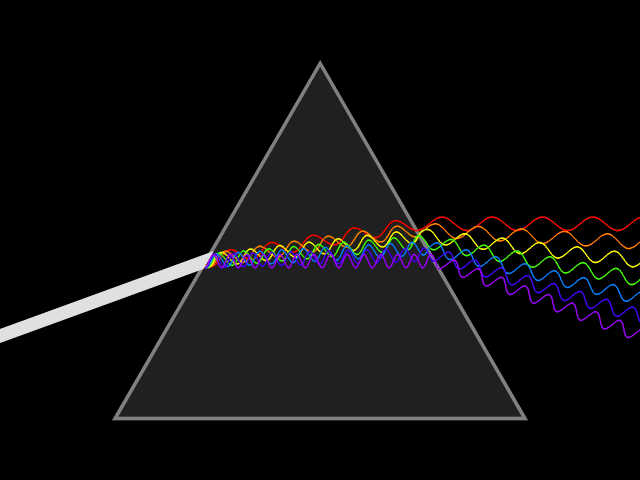
The speed of a wave depends upon the medium in which it propagates. In particular, the speed of light in most media is lower than in vacuum, which means that the same frequency will correspond to a shorter wavelength in the medium than in vacuum. The wavelength in the medium is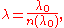

Refractive index
In optics the refractive index or index of refraction of a substance or medium is a measure of the speed of light in that medium. It is expressed as a ratio of the speed of light in vacuum relative to that in the considered medium....
of the medium, which varies with wavelength. This variation, called dispersion
Dispersion (optics)
In optics, dispersion is the phenomenon in which the phase velocity of a wave depends on its frequency, or alternatively when the group velocity depends on the frequency.Media having such a property are termed dispersive media...
, causes different colors of light to be separated when light is refracted
Refraction
Refraction is the change in direction of a wave due to a change in its speed. It is essentially a surface phenomenon . The phenomenon is mainly in governance to the law of conservation of energy. The proper explanation would be that due to change of medium, the phase velocity of the wave is changed...
by a prism
Dispersive prism
In optics, a dispersive prism is a type of optical prism, normally having the shape of a geometrical triangular prism. It is the most widely-known type of optical prism, although perhaps not the most common in actual use. Triangular prisms are used to disperse light, that is, to break light up into...
.
When wavelengths of electromagnetic radiation are quoted, the vacuum wavelength is usually intended unless the wavelength is specifically identified as the wavelength in some other medium. In acoustics, where a medium is essential for the waves to exist, the wavelength value is given for a specified medium.
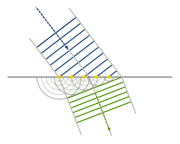
Nonuniform media
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
in space. For example, in an ocean wave approaching shore, shown in the figure, the incoming wave undulates with a varying local wavelength that depends in part on the depth of the sea floor compared to the wave height. The analysis of the wave can be based upon comparison of the local wavelength with the local water depth.
Waves that are sinusoidal in time but propagate through a medium whose properties vary with position (an inhomogeneous medium) may propagate at a velocity that varies with position, and as a result may not be sinusoidal in space. The analysis of differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s of such systems is often done approximately, using the WKB method
WKB approximation
In mathematical physics, the WKB approximation or WKB method is a method for finding approximate solutions to linear partial differential equations with spatially varying coefficients...
(also known as the Liouville–Green method). The method integrates phase through space using a local wavenumber
Wavenumber
In the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
, which can be interpreted as indicating a "local wavelength" of the solution as a function of time and space.
This method treats the system locally as if it were uniform with the local properties; in particular, the local wave velocity associated with a frequency is the only thing needed to estimate the corresponding local wavenumber or wavelength. In addition, the method computes a slowly changing amplitude to satisfy other constraints of the equations or of the physical system, such as for conservation of energy
Conservation of energy
The nineteenth century law of conservation of energy is a law of physics. It states that the total amount of energy in an isolated system remains constant over time. The total energy is said to be conserved over time...
in the wave.
Crystals
Aliasing
In signal processing and related disciplines, aliasing refers to an effect that causes different signals to become indistinguishable when sampled...
because the same vibration can be considered to have a variety of different wavelengths, as shown in the figure. Descriptions using more than one of these wavelengths are redundant; it is conventional to choose the longest wavelength that fits the phenomenon. The range of wavelengths sufficient to provide a description of all possible waves in a crystalline medium corresponds to the wave vectors confined to the Brillouin zone
Brillouin zone
In mathematics and solid state physics, the first Brillouin zone is a uniquely defined primitive cell in reciprocal space. The boundaries of this cell are given by planes related to points on the reciprocal lattice. It is found by the same method as for the Wigner–Seitz cell in the Bravais lattice...
.
This indeterminacy in wavelength in solids is important in the analysis of wave phenomena such as energy bands and lattice vibrations. It is mathematically equivalent to the aliasing
Aliasing
In signal processing and related disciplines, aliasing refers to an effect that causes different signals to become indistinguishable when sampled...
of a signal that is sampled
Sampling (signal processing)
In signal processing, sampling is the reduction of a continuous signal to a discrete signal. A common example is the conversion of a sound wave to a sequence of samples ....
at discrete intervals.
More general waveforms
A wave moving in space is called a traveling wave. If the shape repeats itself, it is also a periodic wave.In the special case of uniform and dispersionless media (see Dispersion relation
Dispersion relation
In physics and electrical engineering, dispersion most often refers to frequency-dependent effects in wave propagation. Note, however, that there are several other uses of the word "dispersion" in the physical sciences....
), at a fixed moment in time, a snapshot of the wave shows a repeating form in space, with characteristics such as peaks and troughs repeating at equal intervals. To an observer at a fixed location the amplitude appears to vary in time, and repeats itself with a certain period, for example T. If the spatial period of this wave is referred to as its wavelength, then during every period, one wavelength of the wave passes the observer. In dispersion and uniform media, the wave propagates with unchanging shape and the velocity in the medium is uniform, so this period implies the wavelength is:


Traveling waves with non-sinusoidal wave shapes can occur in linear dispersionless
Dispersion (optics)
In optics, dispersion is the phenomenon in which the phase velocity of a wave depends on its frequency, or alternatively when the group velocity depends on the frequency.Media having such a property are termed dispersive media...
media such as free space, but also may arise in nonlinear media under certain circumstances. For example, large-amplitude ocean waves with certain shapes can propagate unchanged, because of properties of the nonlinear surface-wave medium. An example is the cnoidal wave
Cnoidal wave
In fluid dynamics, a cnoidal wave is a nonlinear and exact periodic wave solution of the Korteweg–de Vries equation. These solutions are in terms of the Jacobi elliptic function cn, which is why they are coined cnoidal waves...
, a periodic traveling wave named because it is described by the Jacobi elliptic function of m-th order, usually denoted as cn (x; m).
Envelope waves
The term wavelength is also sometimes applied to the envelopesEnvelope (mathematics)
In geometry, an envelope of a family of curves in the plane is a curve that is tangent to each member of the family at some point. Classically, a point on the envelope can be thought of as the intersection of two "adjacent" curves, meaning the limit of intersections of nearby curves...
of waves, such as the traveling sinusoidal envelope patterns that result from the interference of two sinusoidal waves close in frequency; such envelope characterizations are used in illustrating the derivation of group velocity
Group velocity
The group velocity of a wave is the velocity with which the overall shape of the wave's amplitudes — known as the modulation or envelope of the wave — propagates through space....
, the speed at which slow envelope variations propagate.
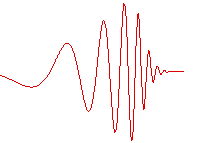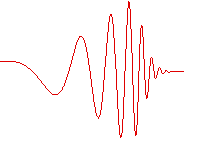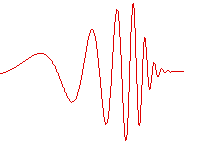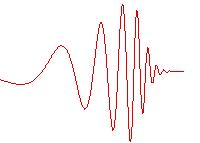
Wave packets
.gif)
Localized wave packet
Wave packet
In physics, a wave packet is a short "burst" or "envelope" of wave action that travels as a unit. A wave packet can be analyzed into, or can be synthesized from, an infinite set of component sinusoidal waves of different wavenumbers, with phases and amplitudes such that they interfere...
s, "bursts" of wave action where each wave packet travels as a unit, find application in many fields of physics; the notion of a wavelength also may be applied to these wave packets.
The wave packet has an envelope that describes the overall amplitude of the wave; within the envelope, the distance between adjacent peaks or troughs is sometimes called a local wavelength. Using Fourier analysis, wave packets can be analyzed into infinite sums (or integrals) of sinusoidal waves of different wavenumber
Wavenumber
In the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
s or wavelengths.
Louis de Broglie postulated that all particles with a specific value of momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
have a wavelength
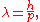
where h is Planck's constant, and p is the momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
of the particle. This hypothesis was at the basis of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. Nowadays, this wavelength is called the de Broglie wavelength. For example, the electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
s in a CRT
Cathode ray tube
The cathode ray tube is a vacuum tube containing an electron gun and a fluorescent screen used to view images. It has a means to accelerate and deflect the electron beam onto the fluorescent screen to create the images. The image may represent electrical waveforms , pictures , radar targets and...
display have a De Broglie wavelength of about 10−13 m. To prevent the wave function for such a particle being spread over all space, De Broglie proposed using wave packets to represent particles that are localized in space. The spread of wavenumber
Wavenumber
In the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
s of sinusoids that add up to such a wave packet corresponds to an uncertainty in the particle's momentum, one aspect of the Heisenberg uncertainty principle.
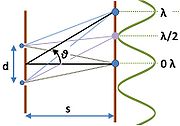
Double-slit interference
Interferometry
Interferometry refers to a family of techniques in which electromagnetic waves are superimposed in order to extract information about the waves. An instrument used to interfere waves is called an interferometer. Interferometry is an important investigative technique in the fields of astronomy,...
. A simple example is an experiment due to Young
Thomas Young (scientist)
Thomas Young was an English polymath. He is famous for having partly deciphered Egyptian hieroglyphics before Jean-François Champollion eventually expanded on his work...
where light is passed through two slits
Double-slit experiment
The double-slit experiment, sometimes called Young's experiment, is a demonstration that matter and energy can display characteristics of both waves and particles...
.
As shown in the figure, light is passed through two slits and shines on a screen. The path of the light to a position on the screen is different for the two slits, and depends upon the angle θ the path makes with the screen. If we suppose the screen is far enough from the slits (that is, s is large compared to the slit separation d) then the paths are nearly parallel, and the path difference is simply d sin θ. Accordingly the condition for constructive interference is:

where m is an integer, and for destructive interference is:

Thus, if the wavelength of the light is known, the slit separation can be determined from the interference pattern or fringes, and vice versa.
It should be noted that the effect of interference is to redistribute the light, so the energy contained in the light is not altered, just where it shows up.
Single-slit diffraction
The notion of path difference and constructive or destructive interference used above for the double-slit experiment applies as well to the display of a single slit of light intercepted on a screen. The main result of this interference is to spread out the light from the narrow slit into a broader image on the screen. This distribution of wave energy is called diffractionDiffraction
Diffraction refers to various phenomena which occur when a wave encounters an obstacle. Italian scientist Francesco Maria Grimaldi coined the word "diffraction" and was the first to record accurate observations of the phenomenon in 1665...
.
Two types of diffraction are distinguished, depending upon the separation between the source and the screen: Fraunhofer diffraction
Fraunhofer diffraction
In optics, the Fraunhofer diffraction equation is used to model the diffraction of waves when the diffraction pattern is viewed at a long distance from the diffracting object, and also when it is viewed at the focal plane of an imaging lens....
or far-field diffraction at large separations and Fresnel diffraction
Fresnel diffraction
In optics, the Fresnel diffraction equation for near-field diffraction, is an approximation of Kirchhoff-Fresnel diffraction that can be applied to the propagation of waves in the near field....
or near-field diffraction at close separations.
In the analysis of the single slit, the non-zero width of the slit is taken into account, and each point in the aperture is taken as the source of one contribution to the beam of light (Huygen's wavelets). On the screen, the light arriving from each position within the slit has a different path length, albeit possibly a very small difference. Consequently, interference occurs.
In the Fraunhofer diffraction pattern sufficiently far from a single slit, within a small-angle approximation, the intensity spread S is related to position x via a squared sinc function:
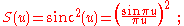 with
with 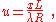
where L is the slit width, R is the distance of the pattern (on the screen) from the slit, and λ is the wavelength of light used. The function S has zeros where u is a non-zero integer, where are at x values at a separation proportion to wavelength.
Diffraction-limited resolution
Diffraction is the fundamental limitation on the resolving powerAngular resolution
Angular resolution, or spatial resolution, describes the ability of any image-forming device such as an optical or radio telescope, a microscope, a camera, or an eye, to distinguish small details of an object...
of optical instruments, such as telescope
Telescope
A telescope is an instrument that aids in the observation of remote objects by collecting electromagnetic radiation . The first known practical telescopes were invented in the Netherlands at the beginning of the 1600s , using glass lenses...
s (including radiotelescopes) and microscopes.
For a circular aperture, the diffraction-limited image spot is known as an Airy disk; the distance x in the single-slit diffraction formula is replaced by radial distance r and the sine is replaced by 2J1, where J1 is a first order Bessel function
Bessel function
In mathematics, Bessel functions, first defined by the mathematician Daniel Bernoulli and generalized by Friedrich Bessel, are canonical solutions y of Bessel's differential equation:...
.
The resolvable spatial size of objects viewed through a microscope is limited according to the Rayleigh criterion, the radius to the first null of the Airy disk, to a size proportional to the wavelength of the light used, and depending on the numerical aperture
Numerical aperture
In optics, the numerical aperture of an optical system is a dimensionless number that characterizes the range of angles over which the system can accept or emit light. By incorporating index of refraction in its definition, NA has the property that it is constant for a beam as it goes from one...
:
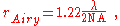
where the numerical aperture is defined as
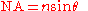 for θ being the half-angle of the cone of rays accepted by the microscope objective.
for θ being the half-angle of the cone of rays accepted by the microscope objective.The angular size of the central bright portion (radius to first null of the Airy disk) of the image diffracted by a circular aperture, a measure most commonly used for telescopes and cameras, is:

where λ is the wavelength of the waves that are focused for imaging, D the entrance pupil
Entrance pupil
In an optical system, the entrance pupil is the optical image of the physical aperture stop, as 'seen' through the front of the lens system. The corresponding image of the aperture as seen through the back of the lens system is called the exit pupil...
diameter of the imaging system, in the same units, and the angular resolution δ is in radians.
As with other diffraction patterns, the pattern scales in proportion to wavelength, so shorter wavelengths can lead to higher resolution.
Subwavelength
The term subwavelength is used to describe an object having one or more dimensions smaller than the length of the wave with which the object interacts. For example, the term subwavelength-diameter optical fibreSubwavelength-diameter optical fibre
Subwavelength-diameter optical fibre is an optical fibre whose diameter is less than the wavelength of the light being propagated through the fibre. An SDOF usually consists of long thick parts at both ends, transition regions Subwavelength-diameter optical fibre (SDF or SDOF) is an optical fibre...
means an optical fibre whose diameter is less than the wavelength of light propagating through it.
A subwavelength particle is a particle smaller than the wavelength of light with which it interacts (see Rayleigh scattering
Rayleigh scattering
Rayleigh scattering, named after the British physicist Lord Rayleigh, is the elastic scattering of light or other electromagnetic radiation by particles much smaller than the wavelength of the light. The particles may be individual atoms or molecules. It can occur when light travels through...
). Subwavelength aperture
Aperture
In optics, an aperture is a hole or an opening through which light travels. More specifically, the aperture of an optical system is the opening that determines the cone angle of a bundle of rays that come to a focus in the image plane. The aperture determines how collimated the admitted rays are,...
s are holes smaller than the wavelength of light propagating through them. Such structures have applications in extraordinary optical transmission
Extraordinary Optical Transmission
Extraordinary optical transmission is the phenomenon of greatly enhanced transmission of light through a subwavelength aperture in an otherwise opaque metallic film which has been patterned with a regularly repeating periodic structure...
, and zero-mode waveguide
Zero-mode waveguide
A zero-mode waveguide is an optical waveguide that guides light energy into a volume that is small in all dimensions compared to the wavelength of the light....
s, among other areas of photonics
Photonics
The science of photonics includes the generation, emission, transmission, modulation, signal processing, switching, amplification, detection and sensing of light. The term photonics thereby emphasizes that photons are neither particles nor waves — they are different in that they have both particle...
.
Subwavelength may also refer to a phenomenon involving subwavelength objects; for example, subwavelength imaging.
Angular wavelength
A quantity related to the wavelength is the angular wavelength (also known as reduced wavelength), usually symbolized by ƛ (lambda-bar). It is equal to the "regular" wavelength "reduced" by a factor of 2π (ƛ = λ/2π). It is usually encountered in quantum mechanics, where it is used in combination with the reduced Planck constant (symbol ħ , h-bar) and the angular frequencyAngular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
(symbol ω) or angular wavenumber (symbol k).
See also
- Emission spectrumEmission spectrumThe emission spectrum of a chemical element or chemical compound is the spectrum of frequencies of electromagnetic radiation emitted by the element's atoms or the compound's molecules when they are returned to a lower energy state....
- Fraunhofer linesFraunhofer linesIn physics and optics, the Fraunhofer lines are a set of spectral lines named for the German physicist Joseph von Fraunhofer . The lines were originally observed as dark features in the optical spectrum of the Sun....
– dark lines in the solar spectrum, traditionally used as standard optical wavelength references - Index of wave articles
- Spectral lineSpectral lineA spectral line is a dark or bright line in an otherwise uniform and continuous spectrum, resulting from a deficiency or excess of photons in a narrow frequency range, compared with the nearby frequencies.- Types of line spectra :...
- SpectrumSpectrumA spectrum is a condition that is not limited to a specific set of values but can vary infinitely within a continuum. The word saw its first scientific use within the field of optics to describe the rainbow of colors in visible light when separated using a prism; it has since been applied by...
- Spectrum analysisSpectrum analysisSpectrum, also known as emission spectrochemical analysis, is the original scientific method of charting and analyzing the chemical properties of matter and gases by looking at the bands in their optical spectrum...

