
Lorentz force
Encyclopedia
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the Lorentz
Hendrik Lorentz
Hendrik Antoon Lorentz was a Dutch physicist who shared the 1902 Nobel Prize in Physics with Pieter Zeeman for the discovery and theoretical explanation of the Zeeman effect...
force is the force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
on a point charge due to electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
s. It is given by the following equation in terms of the electric
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
and magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
s:
where
- F is the forceForceIn physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
(in newtons) - E is the electric fieldElectric fieldIn physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
(in voltVoltThe volt is the SI derived unit for electric potential, electric potential difference, and electromotive force. The volt is named in honor of the Italian physicist Alessandro Volta , who invented the voltaic pile, possibly the first chemical battery.- Definition :A single volt is defined as the...
s per metreMetreThe metre , symbol m, is the base unit of length in the International System of Units . Originally intended to be one ten-millionth of the distance from the Earth's equator to the North Pole , its definition has been periodically refined to reflect growing knowledge of metrology...
) - B is the magnetic fieldMagnetic fieldA magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
(in teslasTesla (unit)The tesla is the SI derived unit of magnetic field B . One tesla is equal to one weber per square meter, and it was defined in 1960 in honour of the inventor, physicist, and electrical engineer Nikola Tesla...
) - q is the electric chargeElectric chargeElectric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
of the particle (in coulombs) - v is the instantaneous velocityVelocityIn physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
of the particle (in metreMetreThe metre , symbol m, is the base unit of length in the International System of Units . Originally intended to be one ten-millionth of the distance from the Earth's equator to the North Pole , its definition has been periodically refined to reflect growing knowledge of metrology...
s per secondSecondThe second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....
) - × is the vector cross product operator
All the quantities written in boldface are vectors.
The Lorentz force law has a close relationship with Faraday's law of induction
Faraday's law of induction
Faraday's law of induction dates from the 1830s, and is a basic law of electromagnetism relating to the operating principles of transformers, inductors, and many types of electrical motors and generators...
.
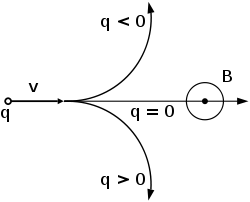
A positively charged particle will be accelerated in the same linear orientation as the E field, but will curve perpendicularly to both the instantaneous velocity vector v and the B field according to the right-hand rule
Right-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
(in detail, if the thumb of the right hand points along v and the index finger along B, then the middle finger points along F).
The term qE is called the electric force, while the term qv × B is called the magnetic force. According to some definitions, the term "Lorentz force" refers specifically to the formula for the magnetic force, with the total electromagnetic force (including the electric force) given some other (nonstandard) name. This article will not follow this nomenclature: In what follows, the term "Lorentz force" will refer only to the expression for the total force.
The magnetic force component of the Lorentz force manifests itself as the force that acts on a current-carrying wire
Wire
A wire is a single, usually cylindrical, flexible strand or rod of metal. Wires are used to bear mechanical loads and to carry electricity and telecommunications signals. Wire is commonly formed by drawing the metal through a hole in a die or draw plate. Standard sizes are determined by various...
in a magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
. In that context, it is also called the Laplace force.
History
Early attempts to quantitatively describe the electromagnetic force were made in the mid-18th century. It was proposed that the force on magnetic poles, by Johann Tobias MayerJohann Tobias Mayer
Johann Tobias Mayer was a German physicist. He was mainly well known for his mathematics and natural science textbooks. Anfangsgründe der Naturlehre zum Behuf der Vorlesungen über die Experimental-Physik, an 1801 physics text, was the most influential of its time in the German-speaking countries...
and others in 1760, and electrically charged objects, by Henry Cavendish
Henry Cavendish
Henry Cavendish FRS was a British scientist noted for his discovery of hydrogen or what he called "inflammable air". He described the density of inflammable air, which formed water on combustion, in a 1766 paper "On Factitious Airs". Antoine Lavoisier later reproduced Cavendish's experiment and...
in 1762, obeyed an inverse-square law
Inverse-square law
In physics, an inverse-square law is any physical law stating that a specified physical quantity or strength is inversely proportional to the square of the distance from the source of that physical quantity....
. However, in both cases the experimental proof was neither complete nor conclusive. It was not until 1784 when Charles-Augustin de Coulomb
Charles-Augustin de Coulomb
Charles-Augustin de Coulomb was a French physicist. He is best known for developing Coulomb's law, the definition of the electrostatic force of attraction and repulsion. The [SI unit] of charge, the coulomb, was named after him....
, using a torsion balance, was able to definitively show through experiment that this was true. Soon after the discovery in 1820 by H. C. Ørsted that a magnetic needle is acted on by a voltaic current, André-Marie Ampère
André-Marie Ampère
André-Marie Ampère was a French physicist and mathematician who is generally regarded as one of the main discoverers of electromagnetism. The SI unit of measurement of electric current, the ampere, is named after him....
that same year was able to devise through experimentation the formula for the angular dependence of the force between two current elements. In all these descriptions, the force was always given in terms of the properties of the objects involved and the distances between them rather than in terms of electric and magnetic fields.
The modern concept of electric and magnetic fields first arose in the theories of Michael Faraday
Michael Faraday
Michael Faraday, FRS was an English chemist and physicist who contributed to the fields of electromagnetism and electrochemistry....
, particularly his idea of lines of force, later to be given full mathematical description by Lord Kelvin
William Thomson, 1st Baron Kelvin
William Thomson, 1st Baron Kelvin OM, GCVO, PC, PRS, PRSE, was a mathematical physicist and engineer. At the University of Glasgow he did important work in the mathematical analysis of electricity and formulation of the first and second laws of thermodynamics, and did much to unify the emerging...
and James Clerk Maxwell
James Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
. From a modern perspective it is possible to identify in Maxwell's 1865 formulation of his field equations a form of the Lorentz force equation in relation to electric currents, however, in the time of Maxwell it was not evident how his equations related to the forces on moving charged objects. J. J. Thomson
J. J. Thomson
Sir Joseph John "J. J." Thomson, OM, FRS was a British physicist and Nobel laureate. He is credited for the discovery of the electron and of isotopes, and the invention of the mass spectrometer...
was the first to attempt to derive from Maxwell's field equations the electromagnetic forces on a moving charged object in terms of the object's properties and external fields. Interested in determining the electromagnetic behavior of the charged particles in cathode ray
Cathode ray
Cathode rays are streams of electrons observed in vacuum tubes. If an evacuated glass tube is equipped with two electrodes and a voltage is applied, the glass opposite of the negative electrode is observed to glow, due to electrons emitted from and travelling perpendicular to the cathode Cathode...
s, Thomson published a paper in 1881 wherein he gave the force on the particles due to an external magnetic field as
 . Thomson was able to arrive at the correct basic form of the formula, but, because of some miscalculations and an incomplete description of the displacement current
. Thomson was able to arrive at the correct basic form of the formula, but, because of some miscalculations and an incomplete description of the displacement currentDisplacement current
In electromagnetism, displacement current is a quantity that is defined in terms of the rate of change of electric displacement field. Displacement current has the units of electric current density, and it has an associated magnetic field just as actual currents do. However it is not an electric...
, included an incorrect scale-factor of a half in front of the formula. It was Oliver Heaviside
Oliver Heaviside
Oliver Heaviside was a self-taught English electrical engineer, mathematician, and physicist who adapted complex numbers to the study of electrical circuits, invented mathematical techniques to the solution of differential equations , reformulated Maxwell's field equations in terms of electric and...
, who had invented the modern vector notation and applied them to Maxwell's field equations, that in 1885 and 1889 fixed the mistakes of Thomson's derivation and arrived at the correct form of the magnetic force on a moving charged object. Finally, in 1892, Hendrik Lorentz
Hendrik Lorentz
Hendrik Antoon Lorentz was a Dutch physicist who shared the 1902 Nobel Prize in Physics with Pieter Zeeman for the discovery and theoretical explanation of the Zeeman effect...
derived the modern day form of the formula for the electromagnetic force which includes the contributions to the total force from both the electric and the magnetic fields. Lorentz began by abandoning the Maxwellian descriptions of the ether and conduction. Instead, Lorentz made a distinction between matter and the luminiferous aether
Luminiferous aether
In the late 19th century, luminiferous aether or ether, meaning light-bearing aether, was the term used to describe a medium for the propagation of light....
and sought to apply the Maxwell equations at a microscopic scale. Using the Heaviside's version of the Maxwell equations for a stationary ether and applying Lagrangian mechanics
Lagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
, Lorentz arrived at the correct and complete form of the force law that now bears his name.
Trajectories of particles in a Lorentz force

Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
of an electrically charged
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
particle (such as an electron
Electron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
or ion
Ion
An ion is an atom or molecule in which the total number of electrons is not equal to the total number of protons, giving it a net positive or negative electrical charge. The name was given by physicist Michael Faraday for the substances that allow a current to pass between electrodes in a...
in a plasma
Plasma (physics)
In physics and chemistry, plasma is a state of matter similar to gas in which a certain portion of the particles are ionized. Heating a gas may ionize its molecules or atoms , thus turning it into a plasma, which contains charged particles: positive ions and negative electrons or ions...
) can be treated as the superposition of a relatively fast circular motion around a point called the guiding center and a relatively slow drift of this point. The drift speeds may differ for various species depending on their charge states, masses, or temperatures, possibly resulting in electric currents or chemical separation.
Significance of the Lorentz force
While the modern Maxwell's equations describe how electrically charged particles and currents or moving charged particles give rise to electric and magnetic fields, the Lorentz force law completes that picture by describing the force acting on a moving point charge q in the presence of electromagnetic fields. The Lorentz force law describes the effect of E and B upon a point charge, but such electromagnetic forces are not the entire picture. Charged particles are possibly coupled to other forces, notably gravity and nuclear forces. Thus, Maxwell's equations do not stand separate from other physical laws, but are coupled to them via the charge and current densities. The response of a point charge to the Lorentz law is one aspect; the generation of E and B by currents and charges is another.In real materials the Lorentz force is inadequate to describe the behavior of charged particles, both in principle and as a matter of computation. The charged particles in a material medium both respond to the E and B fields and generate these fields. Complex transport equations must be solved to determine the time and spatial response of charges, for example, the Boltzmann equation
Boltzmann equation
The Boltzmann equation, also often known as the Boltzmann transport equation, devised by Ludwig Boltzmann, describes the statistical distribution of one particle in rarefied gas...
or the Fokker–Planck equation or the Navier–Stokes equations. For example, see magnetohydrodynamics
Magnetohydrodynamics
Magnetohydrodynamics is an academic discipline which studies the dynamics of electrically conducting fluids. Examples of such fluids include plasmas, liquid metals, and salt water or electrolytes...
, fluid dynamics
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
, electrohydrodynamics
Electrohydrodynamics
Electrohydrodynamics , also known as electro-fluid-dynamics or electrokinetics, is the study of the dynamics of electrically charged fluids. It is the study of the motions of ionised particles or molecules and their interactions with electric fields and the surrounding fluid...
, superconductivity
Superconductivity
Superconductivity is a phenomenon of exactly zero electrical resistance occurring in certain materials below a characteristic temperature. It was discovered by Heike Kamerlingh Onnes on April 8, 1911 in Leiden. Like ferromagnetism and atomic spectral lines, superconductivity is a quantum...
, stellar evolution
Stellar evolution
Stellar evolution is the process by which a star undergoes a sequence of radical changes during its lifetime. Depending on the mass of the star, this lifetime ranges from only a few million years to trillions of years .Stellar evolution is not studied by observing the life of a single...
. An entire physical apparatus for dealing with these matters has developed. See for example, Green–Kubo relations and Green's function (many-body theory)
Green's function (many-body theory)
In many-body theory, the term Green's function is sometimes used interchangeably with correlation function, but refers specifically to correlators of field operators or creation and annihilation operators....
.
Lorentz force law as the definition of E and B
In many textbook treatments of classical electromagnetism, the Lorentz Force Law is used as the definition of the electric and magnetic fields E and B. To be specific, the Lorentz Force is understood to be the following empirical statement:- The electromagnetic force on a test charge at a given point and time is a certain function of its charge and velocity, which can be parameterized by exactly two vectors E and B, in the functional form:
If this empirical statement is valid (and, of course, countless experiments have shown that it is), then two vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s E and B are thereby defined throughout space and time, and these are called the "electric field" and "magnetic field".
Note that the fields are defined everywhere in space and time, regardless of whether or not a charge is present to experience the force. In particular, the fields are defined with respect to what force a test charge would feel, if it were hypothetically placed there.
Note also that as a definition of E and B, the Lorentz force is only a definition in principle because a real particle (as opposed to the hypothetical "test charge" of infinitesimally-small mass and charge) would generate its own finite E and B fields, which would alter the electromagnetic force that it experiences. In addition, if the charge experiences acceleration, for example, if forced into a curved trajectory by some external agency, it emits radiation that causes braking of its motion. See, for example, Bremsstrahlung
Bremsstrahlung
Bremsstrahlung is electromagnetic radiation produced by the deceleration of a charged particle when deflected by another charged particle, typically an electron by an atomic nucleus. The moving particle loses kinetic energy, which is converted into a photon because energy is conserved. The term is...
and synchrotron light
Synchrotron light
A synchrotron light source is a source of electromagnetic radiation produced by a synchrotron, which is artificially produced for scientific and technical purposes by specialized particle accelerators, typically accelerating electrons...
. These effects occur through both a direct effect (called the radiation reaction force
Abraham-Lorentz force
In the physics of electromagnetism, the Abraham–Lorentz force is the recoil force on an accelerating charged particle caused by the particle emitting electromagnetic radiation. It is also called the radiation reaction force....
) and indirectly (by affecting the motion of nearby charges and currents).
Moreover, the electromagnetic force is not in general the same as the net force, due to gravity, electroweak
Electroweak interaction
In particle physics, the electroweak interaction is the unified description of two of the four known fundamental interactions of nature: electromagnetism and the weak interaction. Although these two forces appear very different at everyday low energies, the theory models them as two different...
and other forces, and any extra forces would have to be taken into account in a real measurement.
Lorentz force and Faraday's law of induction
Given a loop of wire in a magnetic fieldMagnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
, Faraday's law of induction states:

where:
 is the magnetic flux
is the magnetic fluxMagnetic flux
Magnetic flux , is a measure of the amount of magnetic B field passing through a given surface . The SI unit of magnetic flux is the weber...
through the loop,
 is the electromotive force
is the electromotive forceElectromotive force
In physics, electromotive force, emf , or electromotance refers to voltage generated by a battery or by the magnetic force according to Faraday's Law, which states that a time varying magnetic field will induce an electric current.It is important to note that the electromotive "force" is not a...
(EMF) experienced,
- t is time
- The sign of the EMF is determined by Lenz's lawLenz's lawLenz's law is a common way of understanding how electromagnetic circuits must always obey Newton's third law and The Law of Conservation of Energy...
.
Note that this is valid for not only a stationary wire but also for a moving wire.
From the Faraday Law
Faraday's law of induction
Faraday's law of induction dates from the 1830s, and is a basic law of electromagnetism relating to the operating principles of transformers, inductors, and many types of electrical motors and generators...
(that is valid for a moving wire, for instance in a motor) and the Maxwell Equations, the Lorentz Force can be deduced. The reverse is also true, the Lorentz force and the Maxwell Equations can be used to derive the Faraday Law
Faraday's law of induction
Faraday's law of induction dates from the 1830s, and is a basic law of electromagnetism relating to the operating principles of transformers, inductors, and many types of electrical motors and generators...
.
Let
 be the moving wire, moving together without rotation and with constant velocity
be the moving wire, moving together without rotation and with constant velocity  and
and  be the internal surface of the wire. The EMF around the closed path
be the internal surface of the wire. The EMF around the closed path  is given by:
is given by:
where dℓ is an element of the curve
 . The flux ΦB in Faraday's law of induction can be expressed explicitly as:
. The flux ΦB in Faraday's law of induction can be expressed explicitly as:
where
 is a surface bounded by the closed contour
is a surface bounded by the closed contour 
- E is the electric field,
- dℓ is an infinitesimalInfinitesimalInfinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
vector element of the contour ,
, - v is the velocityVelocityIn physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
of the infinitesimal contour element dℓ, - B is the magnetic fieldMagnetic fieldA magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
. - dA is an infinitesimal vector element of surface
 , whose magnitude is the area of an infinitesimal patch of surface, and whose direction is orthogonal to that surface patch.
, whose magnitude is the area of an infinitesimal patch of surface, and whose direction is orthogonal to that surface patch. - Both dℓ and dA have a sign ambiguity; to get the correct sign, the right-hand ruleRight-hand ruleIn mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
is used, as explained in the article Kelvin-Stokes theorem.
The above result can be compared with the version of Faraday's law of induction
Faraday's law of induction
Faraday's law of induction dates from the 1830s, and is a basic law of electromagnetism relating to the operating principles of transformers, inductors, and many types of electrical motors and generators...
that appears in the modern Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
, called here the Maxwell-Faraday equation:

The Maxwell-Faraday equation also can be written in an integral form using the Kelvin-Stokes theorem:.
So we have, the Maxwell Faraday equation:

and the Faraday Law,

The two are equivalent if the wire is not moving. Using the Leibniz integral rule
Leibniz integral rule
In mathematics, Leibniz's rule for differentiation under the integral sign, named after Gottfried Leibniz, tells us that if we have an integral of the formthen for x \in the derivative of this integral is thus expressible...
and that div B = 0, results in,

and using the Maxwell Faraday equation,

since this is valid for any wire position it implies that,

Faraday's law of induction holds whether the loop of wire is rigid and stationary, or in motion or in process of deformation, and it holds whether the magnetic field is constant in time or changing. However, there are cases where Faraday's law is either inadequate or difficult to use, and application of the underlying Lorentz force law is necessary. See inapplicability of Faraday's law.
If the magnetic field is fixed in time and the conducting loop moves through the field, the flux magnetic flux ΦB linking the loop can change in several ways. For example, if the B-field varies with position, and the loop moves to a location with different B-field, ΦB will change. Alternatively, if the loop changes orientation with respect to the B-field, the B•dA differential element will change because of the different angle between B and dA, also changing ΦB. As a third example, if a portion of the circuit is swept through a uniform, time-independent B-field, and another portion of the circuit is held stationary, the flux linking the entire closed circuit can change due to the shift in relative position of the circuit's component parts with time (surface
 time-dependent). In all three cases, Faraday's law of induction then predicts the EMF generated by the change in ΦB.
time-dependent). In all three cases, Faraday's law of induction then predicts the EMF generated by the change in ΦB.Note that the Maxwell Faraday's equation implies that the Electric Field (E) is non conservative when the Magnetic Field (B) varies in time, and is not expressible as the gradient of a scalar field
Scalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
, and not subject to the gradient theorem
Gradient theorem
The gradient theorem, also known as the fundamental theorem of calculus for line integrals, says that a line integral through a gradient field can be evaluated by evaluating the original scalar field at the endpoints of the curve: \phi\left-\phi\left = \int_L...
since its rotational is not zero.
See
Relativistic form of the Lorentz force
Because the electric and magnetic fields are dependent on the velocity of an observer, the relativistic form of the Lorentz force law can best be exhibited starting from a coordinate-independent expression for the electromagnetic and magnetic fields, , and an arbitrary time-direction,
, and an arbitrary time-direction,  , where
, whereand
 is a space-time plane (bivector), which has six degrees of freedom corresponding to translations (rotations in space-time planes) and rotations (rotations in space-space planes). The dot product with the vector
is a space-time plane (bivector), which has six degrees of freedom corresponding to translations (rotations in space-time planes) and rotations (rotations in space-space planes). The dot product with the vector  pulls a vector from the translational part, while the wedge-product creates a space-time trivector, whose dot product with the volume element (the dual above) creates the magnetic field vector from the spatial rotation part. Only the parts of the above two formulas perpendicular to gamma are relevant.
pulls a vector from the translational part, while the wedge-product creates a space-time trivector, whose dot product with the volume element (the dual above) creates the magnetic field vector from the spatial rotation part. Only the parts of the above two formulas perpendicular to gamma are relevant.The relativistic velocity is given by the (time-like) changes in a time-position vector
 , where
, where(which shows our choice for the metric) and the velocity is
Then the Lorentz force law is simply (note that the order is important)
Lorentz force in terms of potentials
If the scalar potential and vector potential replace E and B (see Helmholtz decompositionHelmholtz decomposition
In physics and mathematics, in the area of vector calculus, Helmholtz's theorem, also known as the fundamental theorem of vector calculus, states that any sufficiently smooth, rapidly decaying vector field in three dimensions can be resolved into the sum of an irrotational vector field and a...
), the force becomes:

or, equivalently (making use of the fact that v is a constant; see triple product),

where
- A is the magnetic vector potential
 is the electrostatic potential
is the electrostatic potential - The symbols
 denote gradientGradientIn vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
denote gradientGradientIn vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
, curl, and divergenceDivergenceIn vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
, respectively.
The potentials are related to E and B by


Lorentz force in cgs units
The above-mentioned formulae use SI units which are the most common among experimentalists, technicians, and engineers. In cgs-Gaussian unitsGaussian units
Gaussian units comprise a metric system of physical units. This system is the most common of the several electromagnetic unit systems based on cgs units. It is also called the Gaussian unit system, Gaussian-cgs units, or often just cgs units...
, which are somewhat more common among theoretical physicists, one has instead
where c is the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
. Although this equation looks slightly different, it is completely equivalent, since
one has the following relations:
 ,
,  , and
, and 
where ε0 and μ0 are the vacuum permittivity and vacuum permeability
Vacuum permeability
The physical constant μ0, commonly called the vacuum permeability, permeability of free space, or magnetic constant is an ideal, physical constant, which is the value of magnetic permeability in a classical vacuum...
, respectively. In practice, unfortunately, the subscripts "cgs" and "SI" are always omitted, and the unit system has to be assessed from context.
Covariant form of the Lorentz force
Newton's law of motion can be written in covariant formLorentz covariance
In standard physics, Lorentz symmetry is "the feature of nature that says experimental results are independent of the orientation or the boost velocity of the laboratory through space"...
in terms of the field strength tensor.
-
- where
 is
is  times the proper timeProper timeIn relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
times the proper timeProper timeIn relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
of the particle,- q is the chargeElectric chargeElectric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
, - U is the covariant 4-velocityFour-velocityIn physics, in particular in special relativity and general relativity, the four-velocity of an object is a four-vector that replaces classicalvelocity...
of the particle, defined as:  under the metric signature (-1,1,1,1)
under the metric signature (-1,1,1,1)
- with γ = Lorentz factor defined above, and F is the contravariant electromagnetic tensorElectromagnetic tensorThe electromagnetic tensor or electromagnetic field tensor is a mathematical object that describes the electromagnetic field of a physical system in Maxwell's theory of electromagnetism...
written in terms of fields as:
-
 .
.
The fields are transformed to a frame moving with constant relative velocity by:

where is a Lorentz transformationLorentz transformationIn physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
is a Lorentz transformationLorentz transformationIn physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
.
Alternatively, using the four vector:

related to the electric and magnetic fields by:


the field tensor becomes:

where:
Translation to vector notation
The component (x-component) of the force is
component (x-component) of the force is
Here, is the proper timeProper timeIn relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
is the proper timeProper timeIn relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
of the particle. Substituting the components of the covariant electromagnetic tensor F yields
Using the components of covariant four-velocityFour-velocityIn physics, in particular in special relativity and general relativity, the four-velocity of an object is a four-vector that replaces classicalvelocity...
yields
The calculation of the or
or  is similar yielding
is similar yielding
or, in terms of the vector and scalar potentials A and φ,
which are the relativistic forms of Newton's law of motion when the Lorentz force is the only force present.
Force on a current-carrying wire
When a wire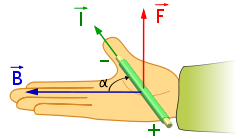 WireA wire is a single, usually cylindrical, flexible strand or rod of metal. Wires are used to bear mechanical loads and to carry electricity and telecommunications signals. Wire is commonly formed by drawing the metal through a hole in a die or draw plate. Standard sizes are determined by various...
WireA wire is a single, usually cylindrical, flexible strand or rod of metal. Wires are used to bear mechanical loads and to carry electricity and telecommunications signals. Wire is commonly formed by drawing the metal through a hole in a die or draw plate. Standard sizes are determined by various...
carrying an electrical current is placed in a magnetic field, each of the moving charges, which comprise the current, experiences the Lorentz force, and together they can create a macroscopic force on the wire (sometimes called the Laplace force). By combining the Lorentz force law above with the definition of electrical current, the following equation results, in the case of a straight, stationary wire:
where- F = Force, measured in newtons
- I = current in wire, measured in amperes
- B = magnetic field vector, measured in teslas
 = vector cross productCross productIn mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
= vector cross productCross productIn mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them... - L = a vector, whose magnitude is the length of wire (measured in metres), and whose direction is along the wire, aligned with the direction of conventional current flow.
Alternatively, some authors write
where the vector direction is now associated with the current variable, instead of the length variable. The two forms are equivalent.
If the wire is not straight but curved, the force on it can be computed by applying this formula to each infinitesimalInfinitesimalInfinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
segment of wire dℓ, then adding up all these forces via integrationIntegralIntegration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
. Formally, the net force on a stationary, rigid wire carrying a current I is
(This is the net force. In addition, there will usually be torqueTorqueTorque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....
, plus other effects if the wire is not perfectly rigid.)
One application of this is Ampère's force lawAmpère's force lawIn magnetostatics, the force of attraction or repulsion between two current-carrying wires is often called Ampère's force law...
, which describes how two current-carrying wires can attract or repel each other, since each experiences a Lorentz force from the other's magnetic field. For more information, see the article: Ampère's force lawAmpère's force lawIn magnetostatics, the force of attraction or repulsion between two current-carrying wires is often called Ampère's force law...
.
EMF
The magnetic force (q v × B) component of the Lorentz force is responsible for motional electromotive forceElectromotive forceIn physics, electromotive force, emf , or electromotance refers to voltage generated by a battery or by the magnetic force according to Faraday's Law, which states that a time varying magnetic field will induce an electric current.It is important to note that the electromotive "force" is not a...
(or motional EMF), the phenomenon underlying many electrical generatorElectrical generatorIn electricity generation, an electric generator is a device that converts mechanical energy to electrical energy. A generator forces electric charge to flow through an external electrical circuit. It is analogous to a water pump, which causes water to flow...
s. When a conductorElectrical conductorIn physics and electrical engineering, a conductor is a material which contains movable electric charges. In metallic conductors such as copper or aluminum, the movable charged particles are electrons...
is moved through a magnetic field, the magnetic force tries to push electrons through the wire, and this creates the EMF. The term "motional EMF" is applied to this phenomenon, since the EMF is due to the motion of the wire.
In other electrical generators, the magnets move, while the conductors do not. In this case, the EMF is due to the electric force (qE) term in the Lorentz Force equation. The electric field in question is created by the changing magnetic field, resulting in an induced EMF, as described by the Maxwell-Faraday equation (one of the four modern Maxwell's equationsMaxwell's equationsMaxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
).
Both of these EMF's, despite their different origins, can be described by the same equation, namely, the EMF is the rate of change of magnetic fluxMagnetic fluxMagnetic flux , is a measure of the amount of magnetic B field passing through a given surface . The SI unit of magnetic flux is the weber...
through the wire. (This is Faraday's law of induction, see above.) Einstein's theory of special relativity was partially motivated by the desire to better understand this link between the two effects. In fact, the electric and magnetic fields are different faces of the same electromagnetic field, and in moving from one inertial frame to another, the solenoidal vector field portion of the E-field can change in whole or in part to a B-field or vice versa.
General references
The numbered references refer in part to the list immediately below.- volume 2.
Applications
The Lorentz force occurs in many devices, including:- CyclotronCyclotronIn technology, a cyclotron is a type of particle accelerator. In physics, the cyclotron frequency or gyrofrequency is the frequency of a charged particle moving perpendicularly to the direction of a uniform magnetic field, i.e. a magnetic field of constant magnitude and direction...
s and other circular path particle acceleratorParticle acceleratorA particle accelerator is a device that uses electromagnetic fields to propel charged particles to high speeds and to contain them in well-defined beams. An ordinary CRT television set is a simple form of accelerator. There are two basic types: electrostatic and oscillating field accelerators.In...
s - Mass spectrometers
- Velocity Filters
- Magnetrons
In its manifestation as the Laplace force on an electric current in a conductor, this force occurs in many devices including:
- Electric motorElectric motorAn electric motor converts electrical energy into mechanical energy.Most electric motors operate through the interaction of magnetic fields and current-carrying conductors to generate force...
s - RailgunRailgunA railgun is an entirely electrical gun that accelerates a conductive projectile along a pair of metal rails using the same principles as the homopolar motor. Railguns use two sliding or rolling contacts that permit a large electric current to pass through the projectile. This current interacts...
s - Linear motorLinear motorA linear motor is an electric motor that has had its stator and rotor "unrolled" so that instead of producing a torque it produces a linear force along its length...
s - LoudspeakerLoudspeakerA loudspeaker is an electroacoustic transducer that produces sound in response to an electrical audio signal input. Non-electrical loudspeakers were developed as accessories to telephone systems, but electronic amplification by vacuum tube made loudspeakers more generally useful...
s
- Magnetoplasmadynamic thrusterMagnetoplasmadynamic thrusterThe Magnetoplasmadynamic thruster is a form of electrically powered spacecraft propulsion which uses the Lorentz force to generate thrust...
s - Electrical generatorElectrical generatorIn electricity generation, an electric generator is a device that converts mechanical energy to electrical energy. A generator forces electric charge to flow through an external electrical circuit. It is analogous to a water pump, which causes water to flow...
s - Homopolar generatorHomopolar generatorA homopolar generator is a DC electrical generator comprising an electrically conductive disc rotating in a plane perpendicular to a uniform static magnetic field. A potential difference is created between the center of the disc and the rim, the electrical polarity depending on the direction of...
s - Linear alternatorLinear alternatorA linear alternator is essentially a linear motor used as an electrical generator.An alternator is a type of alternating current electrical generator. The devices are often physically equivalent. The principal difference is in how they are used and which direction the energy flows...
s
See also
- Hall effectHall effectThe Hall effect is the production of a voltage difference across an electrical conductor, transverse to an electric current in the conductor and a magnetic field perpendicular to the current...
- ElectromagnetismElectromagnetismElectromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
- GravitomagnetismGravitomagnetismGravitomagnetism , refers to a set of formal analogies between Maxwell's field equations and an approximation, valid under certain conditions, to the Einstein field equations for general relativity. The most common version of GEM is valid only far from isolated sources, and for slowly moving test...
- Ampère's force lawAmpère's force lawIn magnetostatics, the force of attraction or repulsion between two current-carrying wires is often called Ampère's force law...
- Hendrik LorentzHendrik LorentzHendrik Antoon Lorentz was a Dutch physicist who shared the 1902 Nobel Prize in Physics with Pieter Zeeman for the discovery and theoretical explanation of the Zeeman effect...
- Maxwell's equationsMaxwell's equationsMaxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
- Formulation of Maxwell's equations in special relativityFormulation of Maxwell's equations in special relativityThe covariant formulation of classical electromagnetism refers to ways of writing the laws of classical electromagnetism in a form which is "manifestly covariant" , in the formalism of special relativity...
- Moving magnet and conductor problemMoving magnet and conductor problemThe moving magnet and conductor problem is a famous thought experiment, originating in the 19th century, concerning the intersection of classical electromagnetism and special relativity. In it, the current in a conductor moving with constant velocity, v, with respect to a magnet is calculated in...
- Abraham–Lorentz force
- Larmor formulaLarmor formulaIn physics, in the area of electrodynamics, the Larmor formula is used to calculate the total power radiated by a nonrelativistic point charge as it accelerates. It was first derived by J. J...
- Cyclotron radiationCyclotron radiationCyclotron radiation is electromagnetic radiation emitted by moving charged particles deflected by a magnetic field. The Lorentz force on the particles acts perpendicular to both the magnetic field lines and the particles' motion through them, creating an acceleration of charged particles that...
- Magnetic potentialMagnetic potentialThe term magnetic potential can be used for either of two quantities in classical electromagnetism: the magnetic vector potential, A, and the magnetic scalar potential, ψ...
- MagnetoresistanceMagnetoresistanceMagnetoresistance is the property of a material to change the value of its electrical resistance when an external magnetic field is applied to it. The effect was first discovered by William Thomson in 1856, but he was unable to lower the electrical resistance of anything by more than 5%. This...
- Scalar potentialScalar potentialA scalar potential is a fundamental concept in vector analysis and physics . The scalar potential is an example of a scalar field...
- Helmholtz decompositionHelmholtz decompositionIn physics and mathematics, in the area of vector calculus, Helmholtz's theorem, also known as the fundamental theorem of vector calculus, states that any sufficiently smooth, rapidly decaying vector field in three dimensions can be resolved into the sum of an irrotational vector field and a...
- Guiding centerGuiding centerIn many cases of practical interest, the motion in a magnetic field of an electrically charged particle can be treated as the superposition of a relatively fast circular motion around a point called the guiding center and a relatively slow drift of this point...
- Field lineField lineA field line is a locus that is defined by a vector field and a starting location within the field. Field lines are useful for visualizing vector fields, which are otherwise hard to depict...
External links
- Interactive Java tutorial on the Lorentz force National High Magnetic Field Laboratory
- Lorentz force (demonstration)
- Faraday's law: Tankersley and Mosca
- Notes from Physics and Astronomy HyperPhysics at Georgia State University; see also home page
- Interactive Java applet on the magnetic deflection of a particle beam in a homogeneous magnetic field by Wolfgang Bauer
-


















