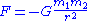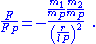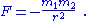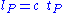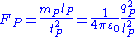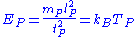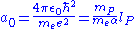Planck units
Encyclopedia
In physics
, Planck units are physical units of measurement
defined exclusively in terms of five universal physical constants listed below, in such a manner that these five physical constants take on the numerical value of 1 when expressed in terms of these units. Planck units elegantly simplify
particular algebraic expression
s appearing in physical law. Originally proposed in 1899 by German physicist Max Planck
, these units are also known as natural units because the origin of their definition comes only from properties of nature
and not from any human construct. Planck units are only one system of natural units
among other systems, but are considered unique in that these units are not based on properties of any prototype object, or particle
(that would be arbitrarily chosen) but are based only on properties of free space. The constants that Planck units, by definition, normalize to 1 are the:
Each of these constants can be associated with at least one fundamental physical theory: c with special relativity
, G with general relativity
and Newtonian gravity, ħ with quantum mechanics
, ε0 with electrostatics
, and kB with statistical mechanics
and thermodynamics
. Planck units have profound significance for theoretical physics since they simplify several recurring algebraic expression
s of physical law
by nondimensionalization
. They are particularly relevant in research on unified theories such as quantum gravity
.
Planck units may sometimes be semi-humorously referred to by physicists as "God's units". They eliminate anthropocentric arbitrariness from the system of units: some physicists argue that communication with extraterrestrial intelligence
would have to use such a system of units to make common reference to scale. Unlike the meter and second
, which exist as fundamental units in the SI
system for historical reasons (in human history), the Planck length and Planck time
are conceptually linked at a fundamental physical level.
Natural units help physicists to reframe questions. Frank Wilczek
puts this succinctly:
The strength of gravity is simply what it is and the strength of the electromagnetic force simply is what it is. The electromagnetic force operates on a different physical quantity (electric charge) than gravity (mass) so it cannot be compared directly to gravity. To note that gravity is an extremely weak force
is, from the point-of-view of Planck units, like comparing apples to oranges. It is true that the electrostatic repulsive force between two protons (alone in free space) greatly exceeds the gravitational attractive force between the same two protons, and that is because the charge on the protons
is approximately the Planck unit of charge
but the mass of the protons is far, far less than the Planck mass.
s: in the International System of Units
(SI), for example, the base unit of length is the meter. In the system of Planck units, the Planck base unit of length is known simply as the Planck length, the base unit of time is the Planck time
, and so on. These units are derived from the five dimensional universal physical constants of Table 1, in such a manner that these constants are eliminated from fundamental equations of physical law when physical quantities are expressed in terms of Planck units. For example, Newton's law of gravitation:
is equivalent to
Both equations are dimensionally consistent
and equally valid in any system of units, but the second equation, with G missing, is relating only dimensionless quantities since any ratio of two like-dimensioned quantities is a dimensionless quantity. If, by a shorthand convention, it is axiomatically understood that all physical quantities are expressed in terms of Planck units, the ratios above may be expressed simply with the symbols of physical quantity, without being scaled by their corresponding unit:
In order for this last equation to be valid (without G present), F, m1, m2, and r are understood to be the dimensionless numerical values of these quantities measured in terms of Planck units. This is why Planck units or any other use of natural units
should be employed with care. Referring to , Paul S. Wesson
wrote that, "Mathematically it is an acceptable trick which saves labour. Physically it represents a loss of information and can lead to confusion."
Key: L = length
, M = mass
, T = time
, Q = electric charge
, Θ = temperature
.
As can be seen above, the gravitational attractive force of two bodies of 1 Planck mass each, set apart by 1 Planck length is 1 Planck force. Likewise, the distance traveled by light during 1 Planck time is 1 Planck length. To determine, in terms of SI
or other existing system of units, the quantitative values of the Planck units, those equations and three others must be satisfied to determine the five unknown quantities that define the Planck units:
Solving the five equations above for the five unknowns results in a unique set of values for the five base Planck units:
Table 2: Base Planck units
Table 3: Derived Planck units
. Table 4 shows how Planck units, by setting the numerical values of five fundamental constants to unity, nondimensionalizes and simplifies many fundamental equations of physics.
Possible alternative normalizations include:
The factor 4π is ubiquitous in theoretical physics
because the surface area of a sphere
is 4πr2. This, along with the concept of flux
is the basis for the inverse-square law
. For example, gravitational
and electrostatic fields produced by point charges have spherical symmetry (Barrow 2002: 214-15). The 4πr2 appearing in the denominator of Coulomb's law
, for example, follows from the flux of an electrostatic field being distributed uniformly on the surface of a sphere. If space had more than three spacial dimensions, the factor 4π would have to be changed.
In 1899, Newton's law of universal gravitation was still seen as fundamental, rather than as a convenient approximation holding for "small" velocities and distances, as general relativity
was to inform us starting in 1915. Hence Planck normalized to 1 the gravitational constant
G in Newton's law. In theories emerging after 1899, G nearly always appears multiplied by 4π or a small integer multiple thereof. Hence a fundamental choice that has to be made when designing a system of natural units is which, if any, instances of 4nπ appearing in the equations of physics are to be eliminated via the normalization:
Hence a substantial body of physical theory discovered since Planck (1899) suggests normalizing to 1 not G but 4nπG, for one of n = 1, 2, or 4. Doing so would introduce a factor of 1/(4nπ) into the nondimensionalized form of the law of universal gravitation, consistent with the modern formulation of Coulomb's law
in terms of the vacuum permittivity. In fact, alternate normalizations frequently preserve the (4π)−1 in the nondimensionalized form of Coulomb's law as well, so that the nondimensionalized Maxwell's equations
for electromagnetism
and gravitomagnetism
both take the same form as those for EM in SI
, which is absent of multiples of 4π.
, the values of those units are only known approximately. This is mostly due to uncertainty in the value of the gravitational constant G.
Today the value of the speed of light c in SI units is not subject to measurement error, because the SI base unit of length, the metre
, is now defined as the length of the path travelled by light in vacuum during a time interval of of a second. Hence the value of c is now exact by definition, and contributes no uncertainty to the SI equivalents of the Planck units. The same is true of the value of the vacuum permittivity ε0, due to the definition of ampere
which sets the vacuum permeability
μ0 to and the fact that μ0ε0 = 1/c2. The numerical value of the reduced Planck constant ℏ has been determined experimentally to 44 parts per billion, while that of G has been determined experimentally to no better than 1 part in 8300. G appears in the definition of almost every Planck unit in Tables 2 and 3. Hence the uncertainty in the values of the Table 2 and 3 SI equivalents of the Planck units derives almost entirely from uncertainty in the value of G. (The propagation of the error in G is a function of the exponent of G in the algebraic expression for a unit. Since that exponent is ± for every base unit other than Planck charge, the relative uncertainty of each base unit is about one half that of G. This is indeed the case; according to CODATA, the experimental values of the SI equivalents of the base Planck units are known to about 1 part in 16,600.)
However, most Planck units are many orders of magnitude too large or too small to be of any practical use, so that Planck units as a system are really only relevant to theoretical physics. In fact, 1 Planck unit is often the largest or smallest value of a physical quantity that makes sense according to our current understanding. For example:
Relative to the Planck Epoch
, the universe today looks extreme when expressed in Planck units, as in this set of approximations (see, for example, and).
The recurrence of the large number 1060 in the above table is a coincidence that intrigues some theorists. It is an example of the kind of large numbers coincidence
that led theorists such as Eddington
and Dirac
to develop alternative physical theories. Theories derived from such coincidences are often dismissed by mainstream physicists as 'numerology'.
began in 1881, when George Johnstone Stoney
, noting that electric charge is quantized, derived units of length, time, and mass, now named Stoney units in his honor, by normalizing G, c, and the electron charge
e to 1. In 1898, Max Planck
discovered that action
is quantized, and published the result in a paper presented to the Prussian Academy of Sciences in May 1899. At the end of the paper, Planck introduced, as a consequence of his discovery, the base units later named in his honor. The Planck units are based on the quantum of action, now usually known as Planck's constant. Planck called the constant b in his paper, though h is now common. Planck underlined the universality of the new unit system, writing:
Planck's paper also gave numerical values for the base units that were close to modern values.
and Milne) have proposed cosmologies
that conjecture that physical "constants" might actually change over time (e.g. Dirac's Large Numbers Hypothesis
). Such cosmologies have not gained mainstream acceptance and yet there is still considerable scientific interest in the possibility that physical 'constants' might change, although such propositions introduce many difficult questions. A few such questions that are relevant here might be: How would such a change make a noticeable operational difference in physical measurement or, more basically, our perception of reality? If some physical constant had changed, how would we notice it? How would physical reality be different? Which changed constants result in a meaningful and measurable differences? If a dimensionful physical constant such as the speed of light did change, would we be able to notice it? George Gamow
argued in his book Mr. Tompkins in Wonderland that any change in a dimensionful physical constant, such as the speed of light in a vacuum, would result in obvious changes.
Referring to Michael Duff (Comment on time-variation of fundamental constants) and Duff, Okun, and Veneziano
(Trialogue on the number of fundamental constants - The operationally indistinguishable world of Mr. Tompkins), if all physical quantities (masses and other properties of particles) were expressed in terms of Planck units, those quantities would be dimensionless numbers (mass divided by the Planck mass, length divided by the Planck length, etc.) and the only quantities that we ultimately measure in physical experiments or in our perception of reality are dimensionless numbers. When one commonly measures a length with a ruler or tape-measure, that person is actually counting tick marks on a given standard or is measuring the length relative to that given standard, which is a dimensionless value. It is no different for physical experiments, as all physical quantities are measured relative to some other like-dimensioned values.
We can notice a difference if some dimensionless physical quantity such as α or the proton/electron mass ratio changes (atomic structures would change) but if all dimensionless physical quantities remained constant (this includes all possible ratios of identically dimensioned physical quantity), we could not tell if a dimensionful quantity, such as the speed of light, c, has changed. And, indeed, the Tompkins concept becomes meaningless in our existence if a dimensional quantity such as c has changed
, even drastically.
If the speed of light c, were somehow suddenly cut in half and changed to , (but with the axiom that all dimensionless physical quantities continuing to remain the same), then the Planck Length would increase by a factor of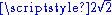
from the point-of-view of some unaffected "god-like" observer on the outside. Measured by "mortal" observers in terms of Planck units, the new speed of light would be remain as 1 new Planck length per 1 new Planck time - which is no different to the old measurement. But, since by axiom, the size of atoms (approximately the Bohr radius
) are related to the Planck length by an unchanging dimensionless constant of proportionality:
Then atoms would be bigger (in one dimension) by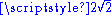
, each of us would be taller by 
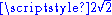, and so would our meter sticks be taller (and wider and thicker) by a factor of 
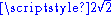. Our perception of distance and lengths relative to the Planck length is, by axiom, an unchanging dimensionless constant.
Our clocks would tick slower by a factor of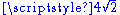
(from the point-of-view of this unaffected "god-like" observer) because the Planck time has increased by 
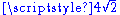but we would not know the difference (our perception of durations of time relative to the Planck time is, by axiom, an unchanging dimensionless constant). This hypothetical god-like observer on the outside might observe that light now travels at half the speed that it used to (as well as all other observed velocities) but it would still travel 299792458
of our new meters in the time elapsed by one of our new seconds (
continues to equal 299792458 m/s). We would not notice any difference.
This contradicts what George Gamow
writes in his book Mr. Tompkins; there, Gamow suggests that if a dimension-dependent universal constant such as c changed, we would easily notice the difference. The disagreement is better thought of as the ambiguity in the phrase "changing a physical constant"; what would happen depends on whether (1) all other dimensionless constants were kept the same, or whether (2) all other dimension-dependent constants are kept the same. The second choice is a somewhat confusing possibility, since most of our units of measurement are defined in relation to the outcomes of physical experiments, and the experimental results depend on the constants. (The only exception is the kilogram
.) Gamow does not address this subtlety; the thought experiments he conducts in his popular works assume the second choice for "changing a physical constant".
This unvarying aspect of the Planck-relative scale, or that of any other system of natural units, leads many theorists to conclude that a hypothetical change in dimensionful physical constants can only be manifest as a change in dimensionless physical constant
s. One such dimensionless physical constant is the fine-structure constant
. There are some experimental physicists who think they have in fact measured a change in the fine structure constant and this has intensified the debate about the measurement of physical constants. According to some theorists there are some very special circumstances in which changes in the fine-structure constant can be measured as a change in dimensionful physical constants. Others however reject the possibility of measuring a change in dimensionful physical constants under any circumstance. The difficulty or even the impossibility of measuring changes in dimensionful physical constants has led some theorists to debate with each other whether or not a dimensionful physical constant has any practical significance at all and that in turn leads to questions about which dimensionful physical constants are meaningful.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, Planck units are physical units of measurement
Units of measurement
A unit of measurement is a definite magnitude of a physical quantity, defined and adopted by convention and/or by law, that is used as a standard for measurement of the same physical quantity. Any other value of the physical quantity can be expressed as a simple multiple of the unit of...
defined exclusively in terms of five universal physical constants listed below, in such a manner that these five physical constants take on the numerical value of 1 when expressed in terms of these units. Planck units elegantly simplify
Nondimensionalization
Nondimensionalization is the partial or full removal of units from an equation involving physical quantities by a suitable substitution of variables. This technique can simplify and parameterize problems where measured units are involved. It is closely related to dimensional analysis...
particular algebraic expression
Algebraic expression
In mathematics, an algebraic expression is an expression that contains only algebraic numbers, variables and algebraic operations. Algebraic operations are addition, subtraction, multiplication, division and exponentiation with integral or fractional exponents...
s appearing in physical law. Originally proposed in 1899 by German physicist Max Planck
Max Planck
Max Karl Ernst Ludwig Planck, ForMemRS, was a German physicist who actualized the quantum physics, initiating a revolution in natural science and philosophy. He is regarded as the founder of the quantum theory, for which he received the Nobel Prize in Physics in 1918.-Life and career:Planck came...
, these units are also known as natural units because the origin of their definition comes only from properties of nature
Nature
Nature, in the broadest sense, is equivalent to the natural world, physical world, or material world. "Nature" refers to the phenomena of the physical world, and also to life in general...
and not from any human construct. Planck units are only one system of natural units
Natural units
In physics, natural units are physical units of measurement based only on universal physical constants. For example the elementary charge e is a natural unit of electric charge, or the speed of light c is a natural unit of speed...
among other systems, but are considered unique in that these units are not based on properties of any prototype object, or particle
Elementary particle
In particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...
(that would be arbitrarily chosen) but are based only on properties of free space. The constants that Planck units, by definition, normalize to 1 are the:
- Gravitational constantGravitational constantThe gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
, G; - Reduced Planck constantPlanck constantThe Planck constant , also called Planck's constant, is a physical constant reflecting the sizes of energy quanta in quantum mechanics. It is named after Max Planck, one of the founders of quantum theory, who discovered it in 1899...
, ħ; - Speed of lightSpeed of lightThe speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
in a vacuum, c; - Coulomb constant,
(sometimes ke or k); - Boltzmann constant, kB (sometimes k).
Each of these constants can be associated with at least one fundamental physical theory: c with special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
, G with general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
and Newtonian gravity, ħ with quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, ε0 with electrostatics
Electrostatics
Electrostatics is the branch of physics that deals with the phenomena and properties of stationary or slow-moving electric charges....
, and kB with statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
and thermodynamics
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
. Planck units have profound significance for theoretical physics since they simplify several recurring algebraic expression
Algebraic expression
In mathematics, an algebraic expression is an expression that contains only algebraic numbers, variables and algebraic operations. Algebraic operations are addition, subtraction, multiplication, division and exponentiation with integral or fractional exponents...
s of physical law
Physical law
A physical law or scientific law is "a theoretical principle deduced from particular facts, applicable to a defined group or class of phenomena, and expressible by the statement that a particular phenomenon always occurs if certain conditions be present." Physical laws are typically conclusions...
by nondimensionalization
Nondimensionalization
Nondimensionalization is the partial or full removal of units from an equation involving physical quantities by a suitable substitution of variables. This technique can simplify and parameterize problems where measured units are involved. It is closely related to dimensional analysis...
. They are particularly relevant in research on unified theories such as quantum gravity
Quantum gravity
Quantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
.
Planck units may sometimes be semi-humorously referred to by physicists as "God's units". They eliminate anthropocentric arbitrariness from the system of units: some physicists argue that communication with extraterrestrial intelligence
Extraterrestrial life
Extraterrestrial life is defined as life that does not originate from Earth...
would have to use such a system of units to make common reference to scale. Unlike the meter and second
Second
The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....
, which exist as fundamental units in the SI
Si
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
system for historical reasons (in human history), the Planck length and Planck time
Planck time
In physics, the Planck time, , is the unit of time in the system of natural units known as Planck units. It is the time required for light to travel, in a vacuum, a distance of 1 Planck length...
are conceptually linked at a fundamental physical level.
Natural units help physicists to reframe questions. Frank Wilczek
Frank Wilczek
Frank Anthony Wilczek is a theoretical physicist from the United States and a Nobel laureate. He is currently the Herman Feshbach Professor of Physics at the Massachusetts Institute of Technology ....
puts this succinctly:
The strength of gravity is simply what it is and the strength of the electromagnetic force simply is what it is. The electromagnetic force operates on a different physical quantity (electric charge) than gravity (mass) so it cannot be compared directly to gravity. To note that gravity is an extremely weak force
Fundamental interaction
In particle physics, fundamental interactions are the ways that elementary particles interact with one another...
is, from the point-of-view of Planck units, like comparing apples to oranges. It is true that the electrostatic repulsive force between two protons (alone in free space) greatly exceeds the gravitational attractive force between the same two protons, and that is because the charge on the protons
Elementary charge
The elementary charge, usually denoted as e, is the electric charge carried by a single proton, or equivalently, the absolute value of the electric charge carried by a single electron. This elementary charge is a fundamental physical constant. To avoid confusion over its sign, e is sometimes called...
is approximately the Planck unit of charge
Planck charge
In physics, the Planck charge , is one of the base units in the system of natural units called Planck units. It is a quantity of electric charge defined in terms of fundamental physical constants.The Planck charge is defined as:...
but the mass of the protons is far, far less than the Planck mass.
Base Planck units
All systems of measurement feature base unitFundamental unit
A set of fundamental units is a set of units for physical quantities from which every other unit can be generated.In the language of measurement, quantities are quantifiable aspects of the world, such as time, distance, velocity, mass, momentum, energy, and weight, and units are used to describe...
s: in the International System of Units
International System of Units
The International System of Units is the modern form of the metric system and is generally a system of units of measurement devised around seven base units and the convenience of the number ten. The older metric system included several groups of units...
(SI), for example, the base unit of length is the meter. In the system of Planck units, the Planck base unit of length is known simply as the Planck length, the base unit of time is the Planck time
Planck time
In physics, the Planck time, , is the unit of time in the system of natural units known as Planck units. It is the time required for light to travel, in a vacuum, a distance of 1 Planck length...
, and so on. These units are derived from the five dimensional universal physical constants of Table 1, in such a manner that these constants are eliminated from fundamental equations of physical law when physical quantities are expressed in terms of Planck units. For example, Newton's law of gravitation:
is equivalent to
Both equations are dimensionally consistent
Dimensional analysis
In physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
and equally valid in any system of units, but the second equation, with G missing, is relating only dimensionless quantities since any ratio of two like-dimensioned quantities is a dimensionless quantity. If, by a shorthand convention, it is axiomatically understood that all physical quantities are expressed in terms of Planck units, the ratios above may be expressed simply with the symbols of physical quantity, without being scaled by their corresponding unit:
In order for this last equation to be valid (without G present), F, m1, m2, and r are understood to be the dimensionless numerical values of these quantities measured in terms of Planck units. This is why Planck units or any other use of natural units
Natural units
In physics, natural units are physical units of measurement based only on universal physical constants. For example the elementary charge e is a natural unit of electric charge, or the speed of light c is a natural unit of speed...
should be employed with care. Referring to , Paul S. Wesson
Paul S. Wesson
Paul S. Wesson, B.Sc., Ph.D., D.Sc., F.R.A.S, is a professor of astrophysics and theoretical physics. He was educated at the Universities of London and Cambridge in England, and spent most of his career at the University of Waterloo in Canada...
wrote that, "Mathematically it is an acceptable trick which saves labour. Physically it represents a loss of information and can lead to confusion."
| Constant | Symbol | Dimension | Value in SI International System of Units The International System of Units is the modern form of the metric system and is generally a system of units of measurement devised around seven base units and the convenience of the number ten. The older metric system included several groups of units... units with uncertainties |
|---|---|---|---|
| c | L T −1 | (exact by definition of meter) |
|
| Gravitational constant Gravitational constant The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal... |
G | L3 M−1 T −2 | |
| ħ = h/2π where h is Planck constant |
L2 M T −1 | ||
| Coulomb constant | (4πε0)−1 where ε0 is the permittivity of free space |
(exact by definition of ampere Ampere The ampere , often shortened to amp, is the SI unit of electric current and is one of the seven SI base units. It is named after André-Marie Ampère , French mathematician and physicist, considered the father of electrodynamics... and meter) |
|
| Boltzmann constant | kB | L2 M T −2 Θ−1 |
Key: L = length
Length
In geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire...
, M = mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
, T = time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
, Q = electric charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
, Θ = temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
.
As can be seen above, the gravitational attractive force of two bodies of 1 Planck mass each, set apart by 1 Planck length is 1 Planck force. Likewise, the distance traveled by light during 1 Planck time is 1 Planck length. To determine, in terms of SI
Si
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
or other existing system of units, the quantitative values of the Planck units, those equations and three others must be satisfied to determine the five unknown quantities that define the Planck units:
Solving the five equations above for the five unknowns results in a unique set of values for the five base Planck units:
Derived Planck units
In any system of measurement, units for many physical quantities can be derived from base units. Table 3 offers a sample of derived Planck units, some of which in fact are seldom used. As with the base units, their use is mostly confined to theoretical physics because most of them are too large or too small for empirical or practical use and there are large uncertainties in their values (see Discussion and Uncertainties in values below).Planck units simplify key equations
Physical quantities that have different dimensions (such as time and length) cannot be equated even if they are numerically equal (1 second is not the same as 1 metre). In theoretical physics, however, this scruple can be set aside, by a process called nondimensionalizationNondimensionalization
Nondimensionalization is the partial or full removal of units from an equation involving physical quantities by a suitable substitution of variables. This technique can simplify and parameterize problems where measured units are involved. It is closely related to dimensional analysis...
. Table 4 shows how Planck units, by setting the numerical values of five fundamental constants to unity, nondimensionalizes and simplifies many fundamental equations of physics.
| Usual form | Nondimensionalized form | |
|---|---|---|
| Newton's law of universal gravitation Newton's law of universal gravitation Newton's law of universal gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them... |
 |
 |
| Einstein field equations Einstein field equations The Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy... in general relativity General relativity General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics... |
 |
 |
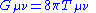| Mass–energy equivalence in special relativity Special relativity Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's... |
 |
 |
| Energy-momentum relation Energy-momentum relation In special relativity, the energy-momentum relation is a relation between the energy, momentum and the mass of a body: E^2 = m^2 c^4 + p^2 c^2 , \;where c is the speed of light, E \; is total energy, m \; is invariant mass, and p = |\vec p|\; is momentum.... |
 |
 |
| Thermal energy Thermal energy Thermal energy is the part of the total internal energy of a thermodynamic system or sample of matter that results in the system's temperature.... per particle per degree of freedom Degrees of freedom (physics and chemistry) A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system... |
 |
 |
| Boltzmann's entropy formula |  |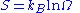
 |
| Planck's relation for energy and angular frequency Angular frequency In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity... |
 |
 |
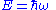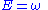| Planck's law (surface intensity Intensity (physics) In physics, intensity is a measure of the energy flux, averaged over the period of the wave. The word "intensity" here is not synonymous with "strength", "amplitude", or "level", as it sometimes is in colloquial speech... per unit solid angle Solid angle The solid angle, Ω, is the two-dimensional angle in three-dimensional space that an object subtends at a point. It is a measure of how large that object appears to an observer looking from that point... per unit angular frequency Angular frequency In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity... ) for black body Black body A black body is an idealized physical body that absorbs all incident electromagnetic radiation. Because of this perfect absorptivity at all wavelengths, a black body is also the best possible emitter of thermal radiation, which it radiates incandescently in a characteristic, continuous spectrum... at temperature Temperature Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot... T. |
 |
 |
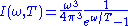| Stefan–Boltzmann constant σ defined |  |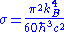
 |
| Bekenstein Jacob Bekenstein Jacob David Bekenstein is an Israeli theoretical physicist who has contributed to the foundation of black hole thermodynamics and to other aspects of the connections between information and gravitation.-Biography:... –Hawking Stephen Hawking Stephen William Hawking, CH, CBE, FRS, FRSA is an English theoretical physicist and cosmologist, whose scientific books and public appearances have made him an academic celebrity... black hole entropy Black hole thermodynamics In physics, black hole thermodynamics is the area of study that seeks to reconcile the laws of thermodynamics with the existence of black hole event horizons... |
 |
 |
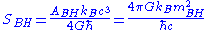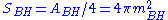| Schrödinger's equation |  |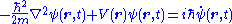
 |
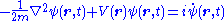| Hamiltonian Hamiltonian (quantum mechanics) In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system... form of Schrödinger's equation |
||
| Covariant form of the Dirac equation Dirac equation The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and... |
 |
 |
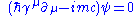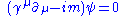| Coulomb's law Coulomb's law Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism... |
 |
 |
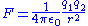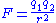| Maxwell's equations Maxwell's equations Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations... |
    |
    |
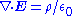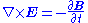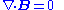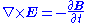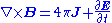Other possible normalizations
As already stated above, Planck units are derived by "normalizing" the numerical values of certain fundamental constants to 1. These normalizations are neither the only ones possible nor necessarily the best. Moreover, the choice of what factors to normalize, among the factors appearing in the fundamental equations of physics, is not evident, and the values of the Planck units are sensitive to this choice.Possible alternative normalizations include:
- The permittivity of free space ε0 = 1.
- Planck normalized to 1 the Coulomb force constant 1/(4πε0) (as does the cgs system of units). This sets the Planck impedance, ZP equal to Z0/4π, where Z0 is the characteristic impedance of free space. On the other hand, if ε0 = 1:
- Sets the permeability of free space µ0 = 1, (because c = 1).
- Equates the unit impedance, ZP, to the characteristic impedance of free space Z0;
- Eliminates 4π from the nondimensionalizedNondimensionalizationNondimensionalization is the partial or full removal of units from an equation involving physical quantities by a suitable substitution of variables. This technique can simplify and parameterize problems where measured units are involved. It is closely related to dimensional analysis...
form of Maxwell's equationsMaxwell's equationsMaxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
; - Introduces a factor of (4π)-1 into the nondimensionalizedNondimensionalizationNondimensionalization is the partial or full removal of units from an equation involving physical quantities by a suitable substitution of variables. This technique can simplify and parameterize problems where measured units are involved. It is closely related to dimensional analysis...
form of Coulomb's lawCoulomb's lawCoulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
.
- Boltzmann constant kB = 2. This:
- Removes the factor of 1/2 in the nondimensionalized equation for the thermal energyThermal energyThermal energy is the part of the total internal energy of a thermodynamic system or sample of matter that results in the system's temperature....
per particle per degree of freedomDegrees of freedom (physics and chemistry)A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...
; - Introduces a factor of 2 into the nondimensionalized form of Boltzmann's entropy formula;
- Does not affect the value of any base or derived Planck unit other than the Planck temperaturePlanck temperaturePlanck temperature is the greatest physically-possible temperature, according the set of theories proposed by the German physicist Max Planck. It's part of a system of five natural units known as Planck units, based on universal physical constants....
.
- Removes the factor of 1/2 in the nondimensionalized equation for the thermal energy
The factor 4π is ubiquitous in theoretical physics
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
because the surface area of a sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
is 4πr2. This, along with the concept of flux
Flux
In the various subfields of physics, there exist two common usages of the term flux, both with rigorous mathematical frameworks.* In the study of transport phenomena , flux is defined as flow per unit area, where flow is the movement of some quantity per time...
is the basis for the inverse-square law
Inverse-square law
In physics, an inverse-square law is any physical law stating that a specified physical quantity or strength is inversely proportional to the square of the distance from the source of that physical quantity....
. For example, gravitational
Gravitational field
The gravitational field is a model used in physics to explain the existence of gravity. In its original concept, gravity was a force between point masses...
and electrostatic fields produced by point charges have spherical symmetry (Barrow 2002: 214-15). The 4πr2 appearing in the denominator of Coulomb's law
Coulomb's law
Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
, for example, follows from the flux of an electrostatic field being distributed uniformly on the surface of a sphere. If space had more than three spacial dimensions, the factor 4π would have to be changed.
In 1899, Newton's law of universal gravitation was still seen as fundamental, rather than as a convenient approximation holding for "small" velocities and distances, as general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
was to inform us starting in 1915. Hence Planck normalized to 1 the gravitational constant
Gravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
G in Newton's law. In theories emerging after 1899, G nearly always appears multiplied by 4π or a small integer multiple thereof. Hence a fundamental choice that has to be made when designing a system of natural units is which, if any, instances of 4nπ appearing in the equations of physics are to be eliminated via the normalization:
- 4πG = 1. This would eliminate the factor 4πG appearing in:
- Gauss's law for gravity, Φg = −4πGM;
- The Bekenstein–Hawking formula for the entropy of a black holeBlack hole thermodynamicsIn physics, black hole thermodynamics is the area of study that seeks to reconcile the laws of thermodynamics with the existence of black hole event horizons...
in terms of its mass mBH and the area of its event horizonEvent horizonIn general relativity, an event horizon is a boundary in spacetime beyond which events cannot affect an outside observer. In layman's terms it is defined as "the point of no return" i.e. the point at which the gravitational pull becomes so great as to make escape impossible. The most common case...
ABH, simplifies to
where ABH and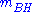 
are both measured in a slight modification of reduced Planck units, described below; - Normalizes the characteristic impedanceCharacteristic impedanceThe characteristic impedance or surge impedance of a uniform transmission line, usually written Z_0, is the ratio of the amplitudes of a single pair of voltage and current waves propagating along the line in the absence of reflections. The SI unit of characteristic impedance is the ohm...
of gravitational radiation in free space, Z0 = 1. In any system of units, Z0 = 4πG/c. General relativityGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
predicts that gravitational radiation propagates at the same speed as electromagnetic radiationSpeed of lightThe speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
; - The gravitoelectromagnetic (GEM) equations, which hold in weak gravitational fieldGravitational fieldThe gravitational field is a model used in physics to explain the existence of gravity. In its original concept, gravity was a force between point masses...
s or reasonably flat space-time. These equations have the same form as Maxwell's equations (and the Lorentz forceLorentz forceIn physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
equation) of electromagnetism, with mass density replacing charge densityCharge densityThe linear, surface, or volume charge density is the amount of electric charge in a line, surface, or volume, respectively. It is measured in coulombs per meter , square meter , or cubic meter , respectively, and represented by the lowercase Greek letter Rho . Since there are positive as well as...
, and with 1/(4πG) replacing ε0.
- 8πG = 1. This would eliminate 8πG from the Einstein field equationsEinstein field equationsThe Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
, Einstein-Hilbert actionEinstein-Hilbert actionThe Einstein–Hilbert action in general relativity is the action that yields the Einstein's field equations through the principle of least action...
, Friedmann equationsFriedmann equationsThe Friedmann equations are a set of equations in physical cosmology that govern the expansion of space in homogeneous and isotropic models of the universe within the context of general relativity...
, and the Poisson equation for gravitation. Planck units modified so that 8πG = 1 are known as reduced Planck units, because the Planck mass is divided by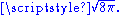
- The Bekenstein–Hawking formula for the entropy of a black holeBlack hole thermodynamicsIn physics, black hole thermodynamics is the area of study that seeks to reconcile the laws of thermodynamics with the existence of black hole event horizons...
simplifies to
and 2πABH.
- The Bekenstein–Hawking formula for the entropy of a black hole
- 16πG = 1. This would eliminate the constant c4/(16πG) from the Einstein-Hilbert actionEinstein-Hilbert actionThe Einstein–Hilbert action in general relativity is the action that yields the Einstein's field equations through the principle of least action...
. The Einstein field equationsEinstein field equationsThe Einstein field equations or Einstein's equations are a set of ten equations in Albert Einstein's general theory of relativity which describe the fundamental interaction of gravitation as a result of spacetime being curved by matter and energy...
with cosmological constantCosmological constantIn physical cosmology, the cosmological constant was proposed by Albert Einstein as a modification of his original theory of general relativity to achieve a stationary universe...
Λ becomes Rμν − Λgμν = (Rgμν − Tμν)/2.
Hence a substantial body of physical theory discovered since Planck (1899) suggests normalizing to 1 not G but 4nπG, for one of n = 1, 2, or 4. Doing so would introduce a factor of 1/(4nπ) into the nondimensionalized form of the law of universal gravitation, consistent with the modern formulation of Coulomb's law
Coulomb's law
Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
in terms of the vacuum permittivity. In fact, alternate normalizations frequently preserve the (4π)−1 in the nondimensionalized form of Coulomb's law as well, so that the nondimensionalized Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
for electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
and gravitomagnetism
Gravitomagnetism
Gravitomagnetism , refers to a set of formal analogies between Maxwell's field equations and an approximation, valid under certain conditions, to the Einstein field equations for general relativity. The most common version of GEM is valid only far from isolated sources, and for slowly moving test...
both take the same form as those for EM in SI
Si
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
, which is absent of multiples of 4π.
Uncertainties in values
Planck units are clearly defined in terms of fundamental constants in Table 2 and yet, relative to other units of measurement such as SIInternational System of Units
The International System of Units is the modern form of the metric system and is generally a system of units of measurement devised around seven base units and the convenience of the number ten. The older metric system included several groups of units...
, the values of those units are only known approximately. This is mostly due to uncertainty in the value of the gravitational constant G.
Today the value of the speed of light c in SI units is not subject to measurement error, because the SI base unit of length, the metre
Metre
The metre , symbol m, is the base unit of length in the International System of Units . Originally intended to be one ten-millionth of the distance from the Earth's equator to the North Pole , its definition has been periodically refined to reflect growing knowledge of metrology...
, is now defined as the length of the path travelled by light in vacuum during a time interval of of a second. Hence the value of c is now exact by definition, and contributes no uncertainty to the SI equivalents of the Planck units. The same is true of the value of the vacuum permittivity ε0, due to the definition of ampere
Ampere
The ampere , often shortened to amp, is the SI unit of electric current and is one of the seven SI base units. It is named after André-Marie Ampère , French mathematician and physicist, considered the father of electrodynamics...
which sets the vacuum permeability
Vacuum permeability
The physical constant μ0, commonly called the vacuum permeability, permeability of free space, or magnetic constant is an ideal, physical constant, which is the value of magnetic permeability in a classical vacuum...
μ0 to and the fact that μ0ε0 = 1/c2. The numerical value of the reduced Planck constant ℏ has been determined experimentally to 44 parts per billion, while that of G has been determined experimentally to no better than 1 part in 8300. G appears in the definition of almost every Planck unit in Tables 2 and 3. Hence the uncertainty in the values of the Table 2 and 3 SI equivalents of the Planck units derives almost entirely from uncertainty in the value of G. (The propagation of the error in G is a function of the exponent of G in the algebraic expression for a unit. Since that exponent is ± for every base unit other than Planck charge, the relative uncertainty of each base unit is about one half that of G. This is indeed the case; according to CODATA, the experimental values of the SI equivalents of the base Planck units are known to about 1 part in 16,600.)
Discussion
Some Planck units are suitable for measuring quantities that are familiar from daily experience. For example:- 1 Planck mass is about 22 micrograms;
- 1 Planck momentum is about 6.5 kg m/s;
- 1 Planck energy is about 500 kWh;
- 1 Planck chargePlanck chargeIn physics, the Planck charge , is one of the base units in the system of natural units called Planck units. It is a quantity of electric charge defined in terms of fundamental physical constants.The Planck charge is defined as:...
is slightly more than 11 elementary chargeElementary chargeThe elementary charge, usually denoted as e, is the electric charge carried by a single proton, or equivalently, the absolute value of the electric charge carried by a single electron. This elementary charge is a fundamental physical constant. To avoid confusion over its sign, e is sometimes called...
s; - 1 Planck impedance is very nearly 30 ohmOhmThe ohm is the SI unit of electrical resistance, named after German physicist Georg Simon Ohm.- Definition :The ohm is defined as a resistance between two points of a conductor when a constant potential difference of 1 volt, applied to these points, produces in the conductor a current of 1 ampere,...
s.
However, most Planck units are many orders of magnitude too large or too small to be of any practical use, so that Planck units as a system are really only relevant to theoretical physics. In fact, 1 Planck unit is often the largest or smallest value of a physical quantity that makes sense according to our current understanding. For example:
- A speed of 1 Planck length per Planck time is the speed of lightSpeed of lightThe speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
in a vacuum, the maximum possible speed in special relativitySpecial relativitySpecial relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
; - Our understanding of the Big BangBig BangThe Big Bang theory is the prevailing cosmological model that explains the early development of the Universe. According to the Big Bang theory, the Universe was once in an extremely hot and dense state which expanded rapidly. This rapid expansion caused the young Universe to cool and resulted in...
begins with the Planck EpochPlanck epochIn physical cosmology, the Planck epoch , named after Max Planck, is the earliest period of time in the history of the universe, from zero to approximately 10−43 seconds , during which, it is believed, quantum effects of gravity were significant...
, when the universe was 1 Planck time old and 1 Planck length in diameter, and had a Planck temperature of 1. At that moment, quantum theoryQuantum mechanicsQuantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
as presently understood becomes applicable. Understanding the universe when it was less than 1 Planck time old requires a theory of quantum gravityQuantum gravityQuantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
that would incorporate quantum effects into general relativityGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
. Such a theory does not yet exist; - At a Planck temperature of 1, all symmetries brokenSymmetry breakingSymmetry breaking in physics describes a phenomenon where small fluctuations acting on a system which is crossing a critical point decide the system's fate, by determining which branch of a bifurcation is taken. To an outside observer unaware of the fluctuations , the choice will appear arbitrary...
since the early Big Bang would be restored, and the four fundamental forcesFundamental interactionIn particle physics, fundamental interactions are the ways that elementary particles interact with one another...
of contemporary physical theory would become one force.
Relative to the Planck Epoch
Planck epoch
In physical cosmology, the Planck epoch , named after Max Planck, is the earliest period of time in the history of the universe, from zero to approximately 10−43 seconds , during which, it is believed, quantum effects of gravity were significant...
, the universe today looks extreme when expressed in Planck units, as in this set of approximations (see, for example, and).
| Feature of present-day universe |
Approximate number of Planck units |
Equivalents |
|---|---|---|
| Age Age of the universe The age of the universe is the time elapsed since the Big Bang posited by the most widely accepted scientific model of cosmology. The best current estimate of the age of the universe is 13.75 ± 0.13 billion years within the Lambda-CDM concordance model... |
8.0 × 1060 tP | 4.3 × 1017 s |
| Diameter | 5.4 x 1061 lP | 8.7 × 1026 m |
| Mass | approx. 1060 mP | 3 × 1052 kg (only counting stars) 1080 protons (sometimes known as the Eddington number Eddington number In astrophysics, the Eddington number, NEdd, is the number of protons in the observable universe. The name honors the British astrophysicist Arthur Eddington who, in 1938, was the first to propose a calculation of NEdd, and to explain why this number could be important for cosmology and the... ) |
| Temperature Cosmic microwave background radiation In cosmology, cosmic microwave background radiation is thermal radiation filling the observable universe almost uniformly.... |
1.9 × 10−32 TP | 2.725 K temperature of the cosmic microwave background radiation Cosmic microwave background radiation In cosmology, cosmic microwave background radiation is thermal radiation filling the observable universe almost uniformly.... |
The recurrence of the large number 1060 in the above table is a coincidence that intrigues some theorists. It is an example of the kind of large numbers coincidence
Dirac large numbers hypothesis
The Dirac large numbers hypothesis is an observation made by Paul Dirac in 1937 relating ratios of size scales in the Universe to that of force scales. The ratios constitute very large, dimensionless numbers: some 40 orders of magnitude in the present cosmological epoch...
that led theorists such as Eddington
Arthur Stanley Eddington
Sir Arthur Stanley Eddington, OM, FRS was a British astrophysicist of the early 20th century. He was also a philosopher of science and a popularizer of science...
and Dirac
Paul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
to develop alternative physical theories. Theories derived from such coincidences are often dismissed by mainstream physicists as 'numerology'.
History
Natural unitsNatural units
In physics, natural units are physical units of measurement based only on universal physical constants. For example the elementary charge e is a natural unit of electric charge, or the speed of light c is a natural unit of speed...
began in 1881, when George Johnstone Stoney
George Johnstone Stoney
George Johnstone Stoney was an Irish physicist most famous for introducing the term electron as the "fundamental unit quantity of electricity"....
, noting that electric charge is quantized, derived units of length, time, and mass, now named Stoney units in his honor, by normalizing G, c, and the electron charge
Elementary charge
The elementary charge, usually denoted as e, is the electric charge carried by a single proton, or equivalently, the absolute value of the electric charge carried by a single electron. This elementary charge is a fundamental physical constant. To avoid confusion over its sign, e is sometimes called...
e to 1. In 1898, Max Planck
Max Planck
Max Karl Ernst Ludwig Planck, ForMemRS, was a German physicist who actualized the quantum physics, initiating a revolution in natural science and philosophy. He is regarded as the founder of the quantum theory, for which he received the Nobel Prize in Physics in 1918.-Life and career:Planck came...
discovered that action
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
is quantized, and published the result in a paper presented to the Prussian Academy of Sciences in May 1899. At the end of the paper, Planck introduced, as a consequence of his discovery, the base units later named in his honor. The Planck units are based on the quantum of action, now usually known as Planck's constant. Planck called the constant b in his paper, though h is now common. Planck underlined the universality of the new unit system, writing:
Planck's paper also gave numerical values for the base units that were close to modern values.
Planck units and the invariant scaling of nature
Some theorists (such as DiracPaul Dirac
Paul Adrien Maurice Dirac, OM, FRS was an English theoretical physicist who made fundamental contributions to the early development of both quantum mechanics and quantum electrodynamics...
and Milne) have proposed cosmologies
Cosmology
Cosmology is the discipline that deals with the nature of the Universe as a whole. Cosmologists seek to understand the origin, evolution, structure, and ultimate fate of the Universe at large, as well as the natural laws that keep it in order...
that conjecture that physical "constants" might actually change over time (e.g. Dirac's Large Numbers Hypothesis
Dirac large numbers hypothesis
The Dirac large numbers hypothesis is an observation made by Paul Dirac in 1937 relating ratios of size scales in the Universe to that of force scales. The ratios constitute very large, dimensionless numbers: some 40 orders of magnitude in the present cosmological epoch...
). Such cosmologies have not gained mainstream acceptance and yet there is still considerable scientific interest in the possibility that physical 'constants' might change, although such propositions introduce many difficult questions. A few such questions that are relevant here might be: How would such a change make a noticeable operational difference in physical measurement or, more basically, our perception of reality? If some physical constant had changed, how would we notice it? How would physical reality be different? Which changed constants result in a meaningful and measurable differences? If a dimensionful physical constant such as the speed of light did change, would we be able to notice it? George Gamow
George Gamow
George Gamow , born Georgiy Antonovich Gamov , was a Russian-born theoretical physicist and cosmologist. He discovered alpha decay via quantum tunneling and worked on radioactive decay of the atomic nucleus, star formation, stellar nucleosynthesis, Big Bang nucleosynthesis, cosmic microwave...
argued in his book Mr. Tompkins in Wonderland that any change in a dimensionful physical constant, such as the speed of light in a vacuum, would result in obvious changes.
Referring to Michael Duff (Comment on time-variation of fundamental constants) and Duff, Okun, and Veneziano
Gabriele Veneziano
Gabriele Veneziano, born in Florence, Italy), is an Italian theoretical physicist and the founder of string theory. . Has spent most of his scientific activities at CERN in Geneva, Switzerland...
(Trialogue on the number of fundamental constants - The operationally indistinguishable world of Mr. Tompkins), if all physical quantities (masses and other properties of particles) were expressed in terms of Planck units, those quantities would be dimensionless numbers (mass divided by the Planck mass, length divided by the Planck length, etc.) and the only quantities that we ultimately measure in physical experiments or in our perception of reality are dimensionless numbers. When one commonly measures a length with a ruler or tape-measure, that person is actually counting tick marks on a given standard or is measuring the length relative to that given standard, which is a dimensionless value. It is no different for physical experiments, as all physical quantities are measured relative to some other like-dimensioned values.
We can notice a difference if some dimensionless physical quantity such as α or the proton/electron mass ratio changes (atomic structures would change) but if all dimensionless physical quantities remained constant (this includes all possible ratios of identically dimensioned physical quantity), we could not tell if a dimensionful quantity, such as the speed of light, c, has changed. And, indeed, the Tompkins concept becomes meaningless in our existence if a dimensional quantity such as c has changed
Variable speed of light
The variable speed of light concept states that the speed of light in a vacuum, usually denoted by c, may not be constant in most cases. In most situations in condensed matter physics when light is traveling through a medium, it effectively has a slower speed...
, even drastically.
If the speed of light c, were somehow suddenly cut in half and changed to , (but with the axiom that all dimensionless physical quantities continuing to remain the same), then the Planck Length would increase by a factor of
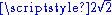from the point-of-view of some unaffected "god-like" observer on the outside. Measured by "mortal" observers in terms of Planck units, the new speed of light would be remain as 1 new Planck length per 1 new Planck time - which is no different to the old measurement. But, since by axiom, the size of atoms (approximately the Bohr radiusBohr radius
The Bohr radius is a physical constant, approximately equal to the most probable distance between the proton and electron in a hydrogen atom in its ground state. It is named after Niels Bohr, due to its role in the Bohr model of an atom...
) are related to the Planck length by an unchanging dimensionless constant of proportionality:
Then atoms would be bigger (in one dimension) by
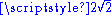, each of us would be taller by 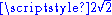, and so would our meter sticks be taller (and wider and thicker) by a factor of 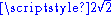. Our perception of distance and lengths relative to the Planck length is, by axiom, an unchanging dimensionless constant.Our clocks would tick slower by a factor of
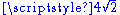(from the point-of-view of this unaffected "god-like" observer) because the Planck time has increased by 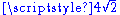but we would not know the difference (our perception of durations of time relative to the Planck time is, by axiom, an unchanging dimensionless constant). This hypothetical god-like observer on the outside might observe that light now travels at half the speed that it used to (as well as all other observed velocities) but it would still travel 299792458Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
of our new meters in the time elapsed by one of our new seconds (
continues to equal 299792458 m/s). We would not notice any difference.This contradicts what George Gamow
George Gamow
George Gamow , born Georgiy Antonovich Gamov , was a Russian-born theoretical physicist and cosmologist. He discovered alpha decay via quantum tunneling and worked on radioactive decay of the atomic nucleus, star formation, stellar nucleosynthesis, Big Bang nucleosynthesis, cosmic microwave...
writes in his book Mr. Tompkins; there, Gamow suggests that if a dimension-dependent universal constant such as c changed, we would easily notice the difference. The disagreement is better thought of as the ambiguity in the phrase "changing a physical constant"; what would happen depends on whether (1) all other dimensionless constants were kept the same, or whether (2) all other dimension-dependent constants are kept the same. The second choice is a somewhat confusing possibility, since most of our units of measurement are defined in relation to the outcomes of physical experiments, and the experimental results depend on the constants. (The only exception is the kilogram
Kilogram
The kilogram or kilogramme , also known as the kilo, is the base unit of mass in the International System of Units and is defined as being equal to the mass of the International Prototype Kilogram , which is almost exactly equal to the mass of one liter of water...
.) Gamow does not address this subtlety; the thought experiments he conducts in his popular works assume the second choice for "changing a physical constant".
This unvarying aspect of the Planck-relative scale, or that of any other system of natural units, leads many theorists to conclude that a hypothetical change in dimensionful physical constants can only be manifest as a change in dimensionless physical constant
Dimensionless physical constant
In physics, a dimensionless physical constant is a universal physical constant that is dimensionless - having no unit attached, so its numerical value is the same under all possible systems of units...
s. One such dimensionless physical constant is the fine-structure constant
Fine-structure constant
In physics, the fine-structure constant is a fundamental physical constant, namely the coupling constant characterizing the strength of the electromagnetic interaction. Being a dimensionless quantity, it has constant numerical value in all systems of units...
. There are some experimental physicists who think they have in fact measured a change in the fine structure constant and this has intensified the debate about the measurement of physical constants. According to some theorists there are some very special circumstances in which changes in the fine-structure constant can be measured as a change in dimensionful physical constants. Others however reject the possibility of measuring a change in dimensionful physical constants under any circumstance. The difficulty or even the impossibility of measuring changes in dimensionful physical constants has led some theorists to debate with each other whether or not a dimensionful physical constant has any practical significance at all and that in turn leads to questions about which dimensionful physical constants are meaningful.
See also
- Dimensional analysisDimensional analysisIn physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
- Doubly special relativity
- Planck scalePlanck scaleIn particle physics and physical cosmology, the Planck scale is an energy scale around 1.22 × 1019 GeV at which quantum effects of gravity become strong...
- Planck particlePlanck particleA Planck particle, named after physicist Max Planck, is a hypothetical particle defined as a tiny black hole whose Compton wavelength is comparable to its Schwarzschild radius. Its mass is thus approximately the Planck mass, and its Compton wavelength and Schwarzschild radius are about the Planck...
- Zero-point energyZero-point energyZero-point energy is the lowest possible energy that a quantum mechanical physical system may have; it is the energy of its ground state. All quantum mechanical systems undergo fluctuations even in their ground state and have an associated zero-point energy, a consequence of their wave-like nature...
- cGh physicsCGh physicscGh physics refers to the mainstream attempts in physics to unify relativity, quantum mechanics, and gravitation, in particular following the ideas of Matvei Petrovich Bronstein and George Gamow...
External links
- Value of the fundamental constants, including the Planck base units, as reported by the National Institute of Standards and TechnologyNational Institute of Standards and TechnologyThe National Institute of Standards and Technology , known between 1901 and 1988 as the National Bureau of Standards , is a measurement standards laboratory, otherwise known as a National Metrological Institute , which is a non-regulatory agency of the United States Department of Commerce...
(NIST). - Sections C-E of collection of resources bear on Planck units. Good discussion of why 8πG should be normalized to 1 when doing general relativityGeneral relativityGeneral relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
and quantum gravityQuantum gravityQuantum gravity is the field of theoretical physics which attempts to develop scientific models that unify quantum mechanics with general relativity...
. Many links. - The universe and the parameters that describe it in Planck units Pulls together various physics concepts into one unifying picture.