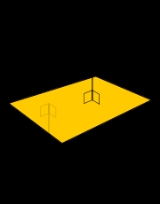
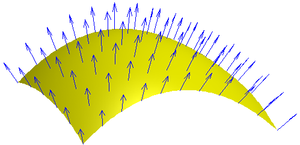
Surface normal
Encyclopedia
Flatness
Flatness may refer to:*Flatness *Flatness *Flatness *Flatness *Flatness , a geometrical tolerance required in certain manufacturing situations*Flatness...
is a vector that is perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
to that surface. A normal to a non-flat surface at a point
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
P on the surface is a vector perpendicular to the tangent plane
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
to that surface at P. The word "normal" is also used as an adjective: a line
Line (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
normal to a plane, the normal component of a force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
, the normal vector, etc. The concept of normality generalizes to orthogonality
Orthogonality
Orthogonality occurs when two things can vary independently, they are uncorrelated, or they are perpendicular.-Mathematics:In mathematics, two vectors are orthogonal if they are perpendicular, i.e., they form a right angle...
.
In the two-dimensional case, a normal line perpendicularly intersects the tangent line to a curve at a given point.
The normal is often used in computer graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
to determine a surface's orientation toward a light source for flat shading, or the orientation of each of the corners (vertices
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
) to mimic a curved surface with Phong shading
Phong shading
Phong shading refers to an interpolation technique for surface shading in 3D computer graphics. It is also called Phong interpolation or normal-vector interpolation shading. Specifically, it interpolates surface normals across rasterized polygons and computes pixel colors based on the interpolated...
.
Calculating a surface normal
For a convexConvex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
(such as a triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
), a surface normal can be calculated as the vector cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
of two (non-parallel) edges of the polygon.
For a plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
given by the equation
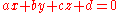 , the vector
, the vector 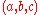 is a normal.
is a normal.For a plane given by the equation
-
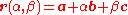 ,
,
i.e., a is a point on the plane and b and c are (non-parallel) vectors lying on the plane, the normal to the plane is a vector normal to both b and c which can be found as the cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
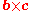 .
.For a hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
in n+1 dimensions, given by the equation
 ,
,where a0 is a point on the hyperplane and ai for i = 1, ... , n are non-parallel vectors lying on the hyperplane, a normal to the hyperplane is any vector in the null space
Null space
In linear algebra, the kernel or null space of a matrix A is the set of all vectors x for which Ax = 0. The kernel of a matrix with n columns is a linear subspace of n-dimensional Euclidean space...
of A where A is given by
-
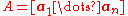 .
.
That is, any vector orthogonal to all in-plane vectors is by definition a surface normal.
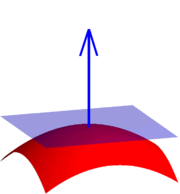
If a (possibly non-flat) surface S is parameterized
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
by a system of curvilinear coordinates
Curvilinear coordinates
Curvilinear coordinates are a coordinate system for Euclidean space in which the coordinate lines may be curved. These coordinates may be derived from a set of Cartesian coordinates by using a transformation that is locally invertible at each point. This means that one can convert a point given...
x(s, t), with s and t real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
variables, then a normal is given by the cross product of the partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s
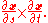
If a surface S is given implicitly
Implicit function
The implicit function theorem provides a link between implicit and explicit functions. It states that if the equation R = 0 satisfies some mild conditions on its partial derivatives, then one can in principle solve this equation for y, at least over some small interval...
as the set of points
 satisfying
satisfying 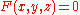 , then, a normal at a point
, then, a normal at a point  on the surface is given by the gradient
on the surface is given by the gradientGradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
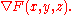
since the gradient at any point is perpendicular to the level set, and
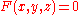 (the surface) is a level set of
(the surface) is a level set of  .
.For a surface S given explicitly as a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
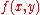 of the independent variables
of the independent variables  (e.g.,
(e.g., 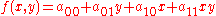 ), its normal can be found in at least two equivalent ways.
), its normal can be found in at least two equivalent ways.The first one is obtaining its implicit form
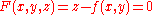 , from which the normal follows readily as the gradient
, from which the normal follows readily as the gradientGradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
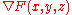 .
.(Notice that the implicit form could be defined alternatively as
 ;
;these two forms correspond to the interpretation of the surface being oriented
Orientability
In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
upwards or downwards, respectively, as a consequence of the difference in the sign of the partial derivative
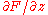 .)
.)The second way of obtaining the normal follows directly from the gradient of the explicit form,
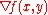 ;
;by inspection,
-
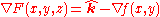 , where
, where  is the upward unit vector.
is the upward unit vector.
If a surface does not have a tangent plane at a point, it does not have a normal at that point either. For example, a cone
Cone (geometry)
A cone is an n-dimensional geometric shape that tapers smoothly from a base to a point called the apex or vertex. Formally, it is the solid figure formed by the locus of all straight line segments that join the apex to the base...
does not have a normal at its tip nor does it have a normal along the edge of its base. However, the normal to the cone is defined almost everywhere
Almost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
. In general, it is possible to define a normal almost everywhere for a surface that is Lipschitz continuous.
Hypersurfaces in n-dimensional space
The definition of a normal to a surface in three-dimensional space can be extended to -dimensional hypersurface
-dimensional hypersurfaceHypersurface
In geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...
s in a
 -dimensional space. A hypersurface may be locally
-dimensional space. A hypersurface may be locallyLocal property
In mathematics, a phenomenon is sometimes said to occur locally if, roughly speaking, it occurs on sufficiently small or arbitrarily small neighborhoods of points.-Properties of a single space:...
defined implicitly as the set of points
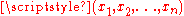 satisfying an equation
satisfying an equation 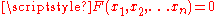 , where
, where  is a given scalar function
is a given scalar functionScalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
. If
 is continuously differentiable, then the hypersurface obtained is a differentiable manifold
is continuously differentiable, then the hypersurface obtained is a differentiable manifoldDifferentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
, and its hypersurface normal can be obtained from the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of
 , in the case it is not null, by the following formula
, in the case it is not null, by the following formula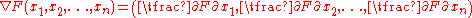
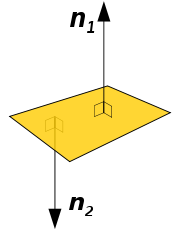
Uniqueness of the normal
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
of a set in three dimensions, one can distinguish between the inward-pointing normal and outer-pointing normal, which can help define the normal in a unique way. For an oriented surface
Orientability
In mathematics, orientability is a property of surfaces in Euclidean space measuring whether or not it is possible to make a consistent choice of surface normal vector at every point. A choice of surface normal allows one to use the right-hand rule to define a "clockwise" direction of loops in the...
, the surface normal is usually determined by the right-hand rule
Right-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
. If the normal is constructed as the cross product of tangent vectors (as described in the text above), it is a pseudovector
Pseudovector
In physics and mathematics, a pseudovector is a quantity that transforms like a vector under a proper rotation, but gains an additional sign flip under an improper rotation such as a reflection. Geometrically it is the opposite, of equal magnitude but in the opposite direction, of its mirror image...
.
Transforming normals
When applying a transform to a surface it is sometimes convenient to derive normals for theresulting surface from the original normals. All points P on tangent plane are transformed
to P′. We want to find n′ perpendicular to P. Let t be a vector on the tangent plane and Ml be the upper 3x3 matrix (translation part of transformation does not apply to normal or tangent vectors).
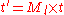

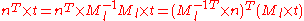
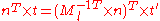
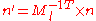
So use the inverse transpose of the linear transformation (the upper 3x3 matrix) when transforming surface normals.
Uses
- Surface normals are essential in defining surface integralSurface integralIn mathematics, a surface integral is a definite integral taken over a surface ; it can be thought of as the double integral analog of the line integral...
s of vector fieldVector fieldIn vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s. - Surface normals are commonly used in 3D computer graphics3D computer graphics3D computer graphics are graphics that use a three-dimensional representation of geometric data that is stored in the computer for the purposes of performing calculations and rendering 2D images...
for lightingLightingLighting or illumination is the deliberate application of light to achieve some practical or aesthetic effect. Lighting includes the use of both artificial light sources such as lamps and light fixtures, as well as natural illumination by capturing daylight...
calculations; see Lambert's cosine lawLambert's cosine lawIn optics, Lambert's cosine law says that the radiant intensity observed from a Lambertian surface or a Lambertian radiator is directly proportional to the cosine of the angle θ between the observer's line of sight and the surface normal. A Lambertian surface is also known as an ideal diffusely...
. - Surface normals are often adjusted in 3D computer graphics3D computer graphics3D computer graphics are graphics that use a three-dimensional representation of geometric data that is stored in the computer for the purposes of performing calculations and rendering 2D images...
by normal mappingNormal mappingIn 3D computer graphics, normal mapping, or "Dot3 bump mapping", is a technique used for faking the lighting of bumps and dents. It is used to add details without using more polygons. A common use of this technique is to greatly enhance the appearance and details of a low polygon model by...
. - Render layersRender layers-What are Render Passes?:When creating computer-generated imagery or 3D computer graphics, final scenes appearing in movies and television productions are usually produced by Rendering more than one "layer" or "pass," which are multiple images designed to be put together through digital...
containing surface normal information may be used in Digital compositingDigital compositingDigital compositing is the process of digitally assembling multiple images to make a final image, typically for print, motion pictures or screen display...
to change the apparent lighting of rendered elements.
Normal in geometric optics

Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
to the surface of an optical medium. The word normal is used here in the mathematical sense, meaning perpendicular. In reflection of light, the angle of incidence
Angle of incidence
Angle of incidence is a measure of deviation of something from "straight on", for example:* in the approach of a ray to a surface, or* the angle at which the wing or horizontal tail of an airplane is installed on the fuselage, measured relative to the axis of the fuselage.-Optics:In geometric...
is the angle between the normal and the incident ray. The angle of reflection is the angle between the normal and the reflected ray.
That Normal force will then Be perpendicular to the surface
External links
- An explanation of normal vectors from Microsoft's MSDN
- Clear pseudocode for calculating a surface normal from either a triangle or polygon.

