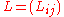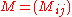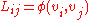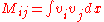Finite element method
Encyclopedia

Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
for finding approximate solutions of partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s (PDE) as well as integral equation
Integral equation
In mathematics, an integral equation is an equation in which an unknown function appears under an integral sign. There is a close connection between differential and integral equations, and some problems may be formulated either way...
s. The solution approach is based either on eliminating the differential equation completely (steady state problems), or rendering the PDE into an approximating system of ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s, which are then numerically integrated using standard techniques such as Euler's method, Runge-Kutta, etc.
In solving partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s, the primary challenge is to create an equation that approximates the equation to be studied, but is numerically stable, meaning that errors in the input and intermediate calculations do not accumulate and cause the resulting output to be meaningless. There are many ways of doing this, all with advantages and disadvantages. The finite element method is a good choice for solving partial differential equations over complicated domains (like cars and oil pipelines), when the domain changes (as during a solid state reaction with a moving boundary), when the desired precision varies over the entire domain, or when the solution lacks smoothness. For instance, in a frontal crash simulation it is possible to increase prediction accuracy in "important" areas like the front of the car and reduce it in its rear (thus reducing cost of the simulation). Another example would be in Numerical weather prediction
Numerical weather prediction
Numerical weather prediction uses mathematical models of the atmosphere and oceans to predict the weather based on current weather conditions. Though first attempted in the 1920s, it was not until the advent of computer simulation in the 1950s that numerical weather predictions produced realistic...
, where it is more important to have accurate predictions over developing highly-nonlinear phenomena (such as tropical cyclones
Tropical cyclone
A tropical cyclone is a storm system characterized by a large low-pressure center and numerous thunderstorms that produce strong winds and heavy rain. Tropical cyclones strengthen when water evaporated from the ocean is released as the saturated air rises, resulting in condensation of water vapor...
in the atmosphere, or eddies
Eddy (fluid dynamics)
In fluid dynamics, an eddy is the swirling of a fluid and the reverse current created when the fluid flows past an obstacle. The moving fluid creates a space devoid of downstream-flowing fluid on the downstream side of the object...
in the ocean) rather than relatively calm areas.
History
The finite element method originated from the need for solving complex elasticityElasticity (physics)
In physics, elasticity is the physical property of a material that returns to its original shape after the stress that made it deform or distort is removed. The relative amount of deformation is called the strain....
and structural analysis
Structural analysis
Structural analysis is the determination of the effects of loads on physical structures and their components. Structures subject to this type of analysis include all that must withstand loads, such as buildings, bridges, vehicles, machinery, furniture, attire, soil strata, prostheses and...
problems in civil
Civil engineering
Civil engineering is a professional engineering discipline that deals with the design, construction, and maintenance of the physical and naturally built environment, including works like roads, bridges, canals, dams, and buildings...
and aeronautical engineering. Its development can be traced back to the work by Alexander Hrennikoff
Alexander Hrennikoff
Alexander Hrennikoff was a Russian-Canadian Structural Engineer, a founder of the Finite Element Method.-Biography:...
(1941) and Richard Courant
Richard Courant
Richard Courant was a German American mathematician.- Life :Courant was born in Lublinitz in the German Empire's Prussian Province of Silesia. During his youth, his parents had to move quite often, to Glatz, Breslau, and in 1905 to Berlin. He stayed in Breslau and entered the university there...
(1942). While the approaches used by these pioneers are different, they share one essential characteristic: mesh
Polygon mesh
A polygon mesh or unstructured grid is a collection of vertices, edges and faces that defines the shape of a polyhedral object in 3D computer graphics and solid modeling...
discretization of a continuous domain into a set of discrete sub-domains, usually called elements. Starting in 1947, Olgierd Zienkiewicz
Olgierd Zienkiewicz
Olgierd Cecil Zienkiewicz, CBE, FREng, FRS was a British academic, mathematician, and civil engineer. He was born in Caterham, England. He was one of the early pioneers of the finite element method...
from Imperial College gathered those methods together into what would be called the Finite Element Method, building the pioneering mathematical formalism of the method.
Hrennikoff's work discretizes the domain by using a lattice
Lattice
Lattice may refer to:In art and design:* Latticework an ornamental criss-crossed framework, an arrangement of crossing laths or other thin strips of material* Lattice In engineering:* A lattice shape truss structure...
analogy, while Courant's approach divides the domain into finite triangular subregions to solve second order elliptic partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s (PDEs) that arise from the problem of torsion
Torsion (mechanics)
In solid mechanics, torsion is the twisting of an object due to an applied torque. In sections perpendicular to the torque axis, the resultant shear stress in this section is perpendicular to the radius....
of a cylinder. Courant's contribution was evolutionary, drawing on a large body of earlier results for PDEs developed by Rayleigh
John Strutt, 3rd Baron Rayleigh
John William Strutt, 3rd Baron Rayleigh, OM was an English physicist who, with William Ramsay, discovered the element argon, an achievement for which he earned the Nobel Prize for Physics in 1904...
, Ritz
Walter Ritz
Walther Ritz was a Swiss theoretical physicist.His father, Raphael Ritz, a native of Valais, was a well-known landscape and interior scenes artist. His mother was the daughter of the engineer Noerdlinger of Tübingen. Ritz studied in Zurich and Göttingen...
, and Galerkin.
Development of the finite element method began in earnest in the middle to late 1950s for airframe
Airframe
The airframe of an aircraft is its mechanical structure. It is typically considered to include fuselage, wings and undercarriage and exclude the propulsion system...
and structural analysis
Structural analysis
Structural analysis is the determination of the effects of loads on physical structures and their components. Structures subject to this type of analysis include all that must withstand loads, such as buildings, bridges, vehicles, machinery, furniture, attire, soil strata, prostheses and...
and gathered momentum at the University of Stuttgart
University of Stuttgart
The University of Stuttgart is a university located in Stuttgart, Germany. It was founded in 1829 and is organized in 10 faculties....
through the work of John Argyris
John Argyris
John Hadji Argyris was among the creators of the Finite Element Method and lately Professor at the University of Stuttgart and Director of the Institute for Statics and Dynamics of Aerospace Structures. His uncle, Constantin Carathéodory, was a Greek mathematician of the Modern Era...
and at Berkeley
University of California, Berkeley
The University of California, Berkeley , is a teaching and research university established in 1868 and located in Berkeley, California, USA...
through the work of Ray W. Clough
Ray W. Clough
Ray William Clough, , was Byron L. and Elvira E. Nishkian Professor of Structural Engineering in the department of Civil Engineering at the University of California, Berkeley and one the founders of the Finite Element Method . His article in 1956 was one of the first applications of this...
in the 1960s for use in civil engineering
Civil engineering
Civil engineering is a professional engineering discipline that deals with the design, construction, and maintenance of the physical and naturally built environment, including works like roads, bridges, canals, dams, and buildings...
. By late 1950s, the key concepts of stiffness matrix and element assembly existed essentially in the form used today. NASA issued a request for proposals for the development of the finite element software NASTRAN
Nastran
NASTRAN is a finite element analysis program that was originally developed for NASA in the late 1960s under United States government funding for the Aerospace industry. The MacNeal-Schwendler Corporation was one of the principal and original developers of the public domain NASTRAN code...
in 1965. The method was again provided with a rigorous mathematical foundation in 1973 with the publication of Strang
Gilbert Strang
William Gilbert Strang , usually known as simply Gilbert Strang or Gil Strang, is a renowned American mathematician, with contributions to finite element theory, the calculus of variations, wavelet analysis and linear algebra...
and Fix
George Fix
George J. Fix was an American mathematician who collaborated on several seminal papers and books in the field of finite element method. In addition to his work in mathematics, Fix was a beer and homebrewing enthusiast and educator, as well as the author of several books about brewing...
's An Analysis of The Finite Element Method, and has since been generalized into a branch of applied mathematics for numerical modeling of physical systems in a wide variety of engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
disciplines, e.g., electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
, thanks to Peter P. Silvester
Peter P. Silvester
Peter Peet Silvester was an electrical engineer who contributed to understanding of numerical analysis of electromagnetic fields and authored a standard textbook on the subject....
and fluid dynamics
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
.
Application

A variety of specializations under the umbrella of the mechanical engineering discipline (such as aeronautical, biomechanical, and automotive industries) commonly use integrated FEM in design and development of their products. Several modern FEM packages include specific components such as thermal, electromagnetic, fluid, and structural working environments. In a structural simulation, FEM helps tremendously in producing stiffness and strength visualizations and also in minimizing weight, materials, and costs.
FEM allows detailed visualization of where structures bend or twist, and indicates the distribution of stresses and displacements. FEM software provides a wide range of simulation options for controlling the complexity of both modeling and analysis of a system. Similarly, the desired level of accuracy required and associated computational time requirements can be managed simultaneously to address most engineering applications. FEM allows entire designs to be constructed, refined, and optimized before the design is manufactured.
This powerful design tool has significantly improved both the standard of engineering designs and the methodology of the design process in many industrial applications. The introduction of FEM has substantially decreased the time to take products from concept to the production line. It is primarily through improved initial prototype designs using FEM that testing and development have been accelerated. In summary, benefits of FEM include increased accuracy, enhanced design and better insight into critical design parameters, virtual prototyping, fewer hardware prototypes, a faster and less expensive design cycle, increased productivity, and increased revenue.
Technical discussion
We will illustrate the finite element method using two sample problems from which the general method can be extrapolated. It is assumed that the reader is familiar with calculusCalculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
and linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
.
P1 is a one-dimensional problem
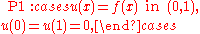
where
 is given,
is given,  is an unknown function of
is an unknown function of  , and
, and  is the second derivative of
is the second derivative of  with respect to
with respect to  .
.The two-dimensional sample problem is the Dirichlet problem
Dirichlet problem
In mathematics, a Dirichlet problem is the problem of finding a function which solves a specified partial differential equation in the interior of a given region that takes prescribed values on the boundary of the region....
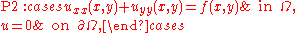
where
 is a connected open region in the
is a connected open region in the 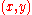 plane whose boundary
plane whose boundary 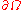 is "nice" (e.g., a smooth manifold or a polygon
is "nice" (e.g., a smooth manifold or a polygonPolygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
), and
 and
and  denote the second derivatives with respect to
denote the second derivatives with respect to  and
and 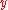 , respectively.
, respectively.The problem P1 can be solved "directly" by computing antiderivative
Antiderivative
In calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
s. However, this method of solving the boundary value problem
Boundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
works only when there is only one spatial dimension and does not generalize to higher-dimensional problems or to problems like
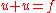 . For this reason, we will develop the finite element method for P1 and outline its generalization to P2.
. For this reason, we will develop the finite element method for P1 and outline its generalization to P2.Our explanation will proceed in two steps, which mirror two essential steps one must take to solve a boundary value problem (BVP) using the FEM.
- In the first step, one rephrases the original BVP in its weak form. Little to no computation is usually required for this step. The transformation is done by hand on paper.
- The second step is the discretization, where the weak form is discretized in a finite dimensional space.
After this second step, we have concrete formulae for a large but finite dimensional linear problem whose solution will approximately solve the original BVP. This finite dimensional problem is then implemented on a computer
Computer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
.
Weak formulation
The first step is to convert P1 and P2 into their equivalent weak formulationsWeak formulation
Weak formulations are an important tool for the analysis of mathematical equations that permit the transfer of concepts of linear algebra to solve problems in other fields such as partial differential equations...
. If
 solves P1, then for any smooth function
solves P1, then for any smooth function  that satisfies the displacement boundary conditions, i.e.
that satisfies the displacement boundary conditions, i.e.  at
at  and
and  , we have
, we have(1)
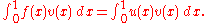
Conversely, if
 with
with  satisfies (1) for every smooth function
satisfies (1) for every smooth function 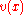 then one may show that this
then one may show that this  will solve P1. The proof is easier for twice continuously differentiable
will solve P1. The proof is easier for twice continuously differentiable  (mean value theorem
(mean value theoremMean value theorem
In calculus, the mean value theorem states, roughly, that given an arc of a differentiable curve, there is at least one point on that arc at which the derivative of the curve is equal to the "average" derivative of the arc. Briefly, a suitable infinitesimal element of the arc is parallel to the...
), but may be proved in a distributional
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
sense as well.
By using integration by parts
Integration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
on the right-hand-side of (1), we obtain
(2)
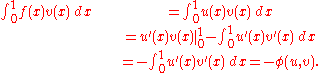
where we have used the assumption that
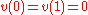 .
.A proof outline of existence and uniqueness of the solution
We can loosely think of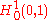 to be the absolutely continuous functions of
to be the absolutely continuous functions of 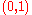 that are
that are  at
at  and
and  (see Sobolev spaces). Such functions are (weakly) "once differentiable" and it turns out that the symmetric bilinear map
(see Sobolev spaces). Such functions are (weakly) "once differentiable" and it turns out that the symmetric bilinear map  then defines an inner product which turns
then defines an inner product which turns 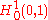 into a Hilbert space
into a Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
(a detailed proof is nontrivial). On the other hand, the left-hand-side
 is also an inner product, this time on the Lp space
is also an inner product, this time on the Lp spaceLp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
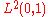 . An application of the Riesz representation theorem
. An application of the Riesz representation theoremRiesz representation theorem
There are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
for Hilbert spaces shows that there is a unique
 solving (2) and therefore P1. This solution is a-priori only a member of
solving (2) and therefore P1. This solution is a-priori only a member of 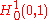 , but using elliptic
, but using ellipticElliptic operator
In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
regularity, will be smooth if
 is.
is.The weak form of P2
If we integrate by parts using a form of Green's identitiesGreen's identities
In mathematics, Green's identities are a set of three identities in vector calculus. They are named after the mathematician George Green, who discovered Green's theorem.-Green's first identity:...
, we see that if
 solves P2, then for any
solves P2, then for any  ,
,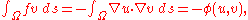
where
 denotes the gradient
denotes the gradientGradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
and
 denotes the dot product
denotes the dot productDot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
in the two-dimensional plane. Once more
 can be turned into an inner product on a suitable space
can be turned into an inner product on a suitable space  of "once differentiable" functions of
of "once differentiable" functions of  that are zero on
that are zero on 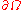 . We have also assumed that
. We have also assumed that 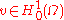 (see Sobolev space
(see Sobolev spaceSobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
s). Existence and uniqueness of the solution can also be shown.
Discretization
- Find
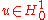 such that
such that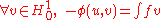
with a finite dimensional version:
Find
 such that
such that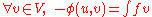
where
 is a finite dimensional subspace
is a finite dimensional subspaceLinear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
of
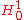 . There are many possible choices for
. There are many possible choices for  (one possibility leads to the spectral method
(one possibility leads to the spectral methodSpectral method
Spectral methods are a class of techniques used in applied mathematics and scientific computing to numerically solve certain Dynamical Systems, often involving the use of the Fast Fourier Transform. Where applicable, spectral methods have excellent error properties, with the so called "exponential...
). However, for the finite element method we take
 to be a space of piecewise polynomial functions.
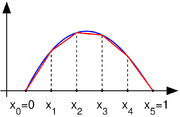
to be a space of piecewise polynomial functions.For problem P1, we take the interval
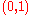 , choose
, choose  values of
values of  with
with  and we define
and we define  by
by
where we define
 and
and 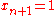 . Observe that functions in
. Observe that functions in  are not differentiable according to the elementary definition of calculus. Indeed, if
are not differentiable according to the elementary definition of calculus. Indeed, if 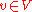 then the derivative is typically not defined at any
then the derivative is typically not defined at any 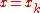 ,
,  . However, the derivative exists at every other value of
. However, the derivative exists at every other value of  and one can use this derivative for the purpose of integration by parts
and one can use this derivative for the purpose of integration by partsIntegration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
.
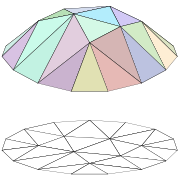
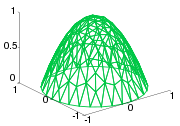
 to be a set of functions of
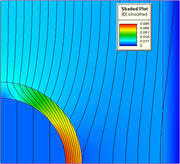
to be a set of functions of  . In the figure on the right, we have illustrated a triangulation
. In the figure on the right, we have illustrated a triangulationPolygon triangulation
In computational geometry, polygon triangulation is the decomposition of a polygonal area P into a set of triangles, i.e., finding the set of triangles with pairwise non-intersecting interiors whose union is P....
of a 15 sided polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
al region
 in the plane (below), and a piecewise linear function (above, in color) of this polygon which is linear on each triangle of the triangulation; the space
in the plane (below), and a piecewise linear function (above, in color) of this polygon which is linear on each triangle of the triangulation; the space  would consist of functions that are linear on each triangle of the chosen triangulation.
would consist of functions that are linear on each triangle of the chosen triangulation.One often reads
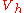 instead of
instead of  in the literature. The reason is that one hopes that as the underlying triangular grid becomes finer and finer, the solution of the discrete problem (3) will in some sense converge to the solution of the original boundary value problem P2. The triangulation is then indexed by a real valued parameter
in the literature. The reason is that one hopes that as the underlying triangular grid becomes finer and finer, the solution of the discrete problem (3) will in some sense converge to the solution of the original boundary value problem P2. The triangulation is then indexed by a real valued parameter  which one takes to be very small. This parameter will be related to the size of the largest or average triangle in the triangulation. As we refine the triangulation, the space of piecewise linear functions
which one takes to be very small. This parameter will be related to the size of the largest or average triangle in the triangulation. As we refine the triangulation, the space of piecewise linear functions  must also change with
must also change with  , hence the notation
, hence the notation 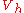 . Since we do not perform such an analysis, we will not use this notation.
. Since we do not perform such an analysis, we will not use this notation.Choosing a basis
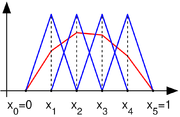
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
of
 . In the one-dimensional case, for each control point
. In the one-dimensional case, for each control point  we will choose the piecewise linear function
we will choose the piecewise linear function  in
in  whose value is
whose value is 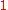 at
at  and zero at every
and zero at every 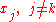 , i.e.,
, i.e.,
for
 ; this basis is a shifted and scaled tent function. For the two-dimensional case, we choose again one basis function
; this basis is a shifted and scaled tent function. For the two-dimensional case, we choose again one basis function 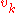 per vertex
per vertex 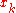 of the triangulation of the planar region
of the triangulation of the planar region  . The function
. The function 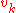 is the unique function of
is the unique function of  whose value is
whose value is 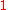 at
at  and zero at every
and zero at every 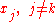 .
.Depending on the author, the word "element" in "finite element method" refers either to the triangles in the domain, the piecewise linear basis function, or both. So for instance, an author interested in curved domains might replace the triangles with curved primitives, and so might describe the elements as being curvilinear. On the other hand, some authors replace "piecewise linear" by "piecewise quadratic" or even "piecewise polynomial". The author might then say "higher order element" instead of "higher degree polynomial". Finite element method is not restricted to triangles (or tetrahedra in 3-d, or higher order simplexes in multidimensional spaces), but can be defined on quadrilateral subdomains (hexahedra, prisms, or pyramids in 3-d, and so on). Higher order shapes (curvilinear elements) can be defined with polynomial and even non-polynomial shapes (e.g. ellipse or circle).
Examples of methods that use higher degree piecewise polynomial basis functions are the
hp-FEM
Hp-FEM
hp-FEM is a general version of the finite element method , a numerical method for solving partial differential equations based on piecewise-polynomial approximations that employs elements of variable size and polynomial degree ...
and spectral FEM
Spectral element method
In mathematics, the spectral element method is a high order finite element method.Introduced in a 1984 paper by A. T. Patera, the abstract begins: "A spectral element method that combines the generality of the finite element method with the accuracy of spectral techniques..."The spectral element...
.
More advanced implementations (adaptive finite element methods) utilize a method to assess the quality of the results (based on error estimation theory) and modify the mesh during the solution aiming to achieve approximate solution within some bounds from the 'exact' solution of the continuum problem. Mesh adaptivity may utilize various techniques, the most popular are:
- moving nodes (r-adaptivity)
- refining (and unrefining) elements (h-adaptivity)
- changing order of base functions (p-adaptivity)
- combinations of the above (hp-adaptivityHp-FEMhp-FEM is a general version of the finite element method , a numerical method for solving partial differential equations based on piecewise-polynomial approximations that employs elements of variable size and polynomial degree ...
)
Small support of the basis


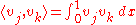
and
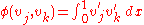
will be zero for almost all
 .
.(The matrix containing
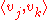 in the
in the 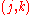 location is known as the Gramian matrix.)
location is known as the Gramian matrix.)In the one dimensional case, the support
Support (mathematics)
In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
of
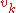 is the interval
is the interval 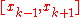 . Hence, the integrands of
. Hence, the integrands of 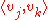 and
and 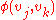 are identically zero whenever
are identically zero whenever 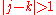 .
.Similarly, in the planar case, if
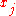 and
and  do not share an edge of the triangulation, then the integrals
do not share an edge of the triangulation, then the integrals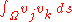
and

are both zero.
Matrix form of the problem
If we write and
and 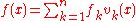 then problem (3), taking
then problem (3), taking 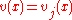 for
for 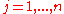 , becomes
, becomes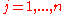 for
for 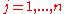 . (4)
. (4)If we denote by
 and
and  the column vectors
the column vectors  and
and  , and if we let
, and if we let
and
be matrices whose entries are
and
then we may rephrase (4) as
-
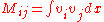 . (5)
. (5)
It is not, in fact, necessary to assume
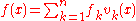 . For a general function
. For a general function 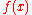 , problem (3) with
, problem (3) with  for
for  becomes actually simpler, since no matrix
becomes actually simpler, since no matrix  is used,
is used,
-
 , (6)
, (6)
where
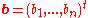 and
and 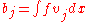 for
for 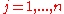 .
.As we have discussed before, most of the entries of
 and
and  are zero because the basis functions
are zero because the basis functions 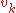 have small support. So we now have to solve a linear system in the unknown
have small support. So we now have to solve a linear system in the unknown  where most of the entries of the matrix
where most of the entries of the matrix 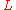 , which we need to invert, are zero.
, which we need to invert, are zero.Such matrices are known as sparse matrices
Sparse matrix
In the subfield of numerical analysis, a sparse matrix is a matrix populated primarily with zeros . The term itself was coined by Harry M. Markowitz....
, and there are efficient solvers for such problems (much more efficient than actually inverting the matrix.) In addition,
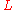 is symmetric and positive definite, so a technique such as the conjugate gradient method
is symmetric and positive definite, so a technique such as the conjugate gradient methodConjugate gradient method
In mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is symmetric and positive-definite. The conjugate gradient method is an iterative method, so it can be applied to sparse systems that are too...
is favored. For problems that are not too large, sparse LU decomposition
LU decomposition
In linear algebra, LU decomposition is a matrix decomposition which writes a matrix as the product of a lower triangular matrix and an upper triangular matrix. The product sometimes includes a permutation matrix as well. This decomposition is used in numerical analysis to solve systems of linear...
s and Cholesky decomposition
Cholesky decomposition
In linear algebra, the Cholesky decomposition or Cholesky triangle is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose. It was discovered by André-Louis Cholesky for real matrices...
s still work well. For instance, Matlab
MATLAB
MATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
's backslash operator (which uses sparse LU, sparse Cholesky, and other factorization methods) can be sufficient for meshes with a hundred thousand vertices.
The matrix
 is usually referred to as the stiffness matrix, while the matrix
is usually referred to as the stiffness matrix, while the matrix  is dubbed the mass matrix
is dubbed the mass matrixMass matrix
In computational mechanics, a mass matrix is a generalization of the concept of mass to generalized coordinates. For example, consider a two-body particle system in one dimension...
.
General form of the finite element method
In general, the finite element method is characterized by the following process.- One chooses a grid for
 . In the preceding treatment, the grid consisted of triangles, but one can also use squares or curvilinear polygons.
. In the preceding treatment, the grid consisted of triangles, but one can also use squares or curvilinear polygons. - Then, one chooses basis functions. In our discussion, we used piecewise linear basis functions, but it is also common to use piecewise polynomial basis functions.
A separate consideration is the smoothness of the basis functions. For second order elliptic boundary value problem
Elliptic boundary value problem
In mathematics, an elliptic boundary value problem is a special kind of boundary value problem which can be thought of as the stable state of an evolution problem...
s, piecewise polynomial basis function that are merely continuous suffice (i.e., the derivatives are discontinuous.) For higher order partial differential equations, one must use smoother basis functions. For instance, for a fourth order problem such as
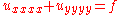 , one may use piecewise quadratic basis functions that are
, one may use piecewise quadratic basis functions that are 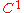 .
.Another consideration is the relation of the finite dimensional space
 to its infinite dimensional counterpart, in the examples above
to its infinite dimensional counterpart, in the examples above 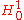 . A conforming element method is one in which the space
. A conforming element method is one in which the space  is a subspace of the element space for the continuous problem. The example above is such a method. If this condition is not satisfied, we obtain a nonconforming element method, an example of which is the space of piecewise linear functions over the mesh which are continuous at each edge midpoint. Since these functions are in general discontinuous along the edges, this finite dimensional space is not a subspace of the original
is a subspace of the element space for the continuous problem. The example above is such a method. If this condition is not satisfied, we obtain a nonconforming element method, an example of which is the space of piecewise linear functions over the mesh which are continuous at each edge midpoint. Since these functions are in general discontinuous along the edges, this finite dimensional space is not a subspace of the original  .
.Typically, one has an algorithm for taking a given mesh and subdividing it. If the main method for increasing precision is to subdivide the mesh, one has an h-method (h is customarily the diameter of the largest element in the mesh.) In this manner, if one shows that the error with a grid
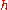 is bounded above by
is bounded above by 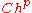 , for some
, for some  and
and  , then one has an order p method. Under certain hypotheses (for instance, if the domain is convex), a piecewise polynomial of order
, then one has an order p method. Under certain hypotheses (for instance, if the domain is convex), a piecewise polynomial of order 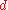 method will have an error of order
method will have an error of order  .
.If instead of making h smaller, one increases the degree of the polynomials used in the basis function, one has a p-method. If one combines these two refinement types, one obtains an hp-method (hp-FEM
Hp-FEM
hp-FEM is a general version of the finite element method , a numerical method for solving partial differential equations based on piecewise-polynomial approximations that employs elements of variable size and polynomial degree ...
). In the hp-FEM, the polynomial degrees can vary from element to element. High order methods with large uniform p are called spectral finite element methods (SFEM
Spectral element method
In mathematics, the spectral element method is a high order finite element method.Introduced in a 1984 paper by A. T. Patera, the abstract begins: "A spectral element method that combines the generality of the finite element method with the accuracy of spectral techniques..."The spectral element...
). These are not to be confused with spectral method
Spectral method
Spectral methods are a class of techniques used in applied mathematics and scientific computing to numerically solve certain Dynamical Systems, often involving the use of the Fast Fourier Transform. Where applicable, spectral methods have excellent error properties, with the so called "exponential...
s.
For vector partial differential equations, the basis functions may take values in
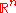 .
.Comparison to the finite difference method
The finite difference methodFinite difference method
In mathematics, finite-difference methods are numerical methods for approximating the solutions to differential equations using finite difference equations to approximate derivatives.- Derivation from Taylor's polynomial :...
(FDM) is an alternative way of approximating solutions of PDEs. The differences between FEM and FDM are:
- The most attractive feature of the FEM is its ability to handle complicated geometries (and boundaries) with relative ease. While FDM in its basic form is restricted to handle rectangular shapes and simple alterations thereof, the handling of geometries in FEM is theoretically straightforward.
- The most attractive feature of finite differences is that it can be very easy to implement.
- There are several ways one could consider the FDM a special case of the FEM approach. E.g., first order FEM is identical to FDM for Poisson's equation, if the problem is discretized by a regular rectangular mesh with each rectangle divided into two triangles.
- There are reasons to consider the mathematical foundation of the finite element approximation more sound, for instance, because the quality of the approximation between grid points is poor in FDM.
- The quality of a FEM approximation is often higher than in the corresponding FDM approach, but this is extremely problem dependent and several examples to the contrary can be provided.
Generally, FEM is the method of choice in all types of analysis in structural mechanics (i.e. solving for deformation and stresses in solid bodies or dynamics of structures) while computational fluid dynamics
Computational fluid dynamics
Computational fluid dynamics, usually abbreviated as CFD, is a branch of fluid mechanics that uses numerical methods and algorithms to solve and analyze problems that involve fluid flows. Computers are used to perform the calculations required to simulate the interaction of liquids and gases with...
(CFD) tends to use FDM or other methods like finite volume method
Finite volume method
The finite volume method is a method for representing and evaluating partial differential equations in the form of algebraic equations [LeVeque, 2002; Toro, 1999]....
(FVM). CFD problems usually require discretization of the problem into a large number of cells/gridpoints (millions and more), therefore cost of the solution favors simpler, lower order approximation within each cell. This is especially true for 'external flow' problems, like air flow around the car or airplane, or weather simulation in a large area.
AEM
The Applied Element Method, or AEM combines features of both FEM and Discrete element methodDiscrete element method
A discrete element method , also called a distinct element method is any of family of numerical methods for computing the motion of a large number of particles of micrometre-scale size and above...
, or (DEM).
Generalized finite element method
The Generalized Finite Element Method (GFEM) uses local spaces consisting of functions, not necessarily polynomials, that reflect the available information on the unknown solution and thus ensure good local approximation. Then a partition of unity is used to “bond” these spaces together to form the approximating subspace. The effectiveness of GFEM has been shown when applied to problems with domains having complicated boundaries, problems with micro-scales, and problems with boundary layers.hp-FEM
The hp-FEMHp-FEM
hp-FEM is a general version of the finite element method , a numerical method for solving partial differential equations based on piecewise-polynomial approximations that employs elements of variable size and polynomial degree ...
combines adaptively elements with variable size h and polynomial degree p in order to achieve exceptionally fast, exponential convergence rates.
hpk-FEM
The hpk-FEM combines adaptively elements with variable size h, polynomial degree of the local approximations p and global differentiability of the local approximations (k-1) in order to achieve best convergence rates.Other applications of finite elements analysis
FEA has also been proposed to use in stochastic modelling, for numerically solving probability models.See the references list
.
See also
- Applied element methodApplied element methodThe Applied Element Method is a numerical analysis used in predicting the continuum and discrete behavior of structures. The modeling method in AEM adopts the concept of discrete cracking allowing it to automatically track structural collapse behavior passing through all stages of loading:...
- Boundary element methodBoundary element methodThe boundary element method is a numerical computational method of solving linear partial differential equations which have been formulated as integral equations . It can be applied in many areas of engineering and science including fluid mechanics, acoustics, electromagnetics, and fracture...
- Direct stiffness methodDirect stiffness methodAs one of the methods of structural analysis, the direct stiffness method , also known as the displacement method or matrix stiffness method, is particularly suited for computer-automated analysis of complex structures including the statically indeterminate type...
- Discontinuity layout optimizationDiscontinuity layout optimizationDiscontinuity layout optimization is an engineering analysis procedure which can be used to directly establish the amount of load that can be carried by a solid or structure prior to collapse...
- Discrete element methodDiscrete element methodA discrete element method , also called a distinct element method is any of family of numerical methods for computing the motion of a large number of particles of micrometre-scale size and above...
- Finite element machineFinite element machineThe Finite Element Machine was a late 1970s-early 1980s NASA project to build and evaluate the performance of a parallel computer for structural analysis. The FEM was completed and successfully tested at the NASA Langley Research Center in Hampton, Virginia...
- Finite element method in structural mechanicsFinite element method in structural mechanicsThe Finite element method is a powerful technique originally developed for numerical solution of complex problems in structural mechanics, and it remains the method of choice for complex systems. In the FEM, the structural system is modeled by a set of appropriate finite elements interconnected at...
- Galerkin methodGalerkin methodIn mathematics, in the area of numerical analysis, Galerkin methods are a class of methods for converting a continuous operator problem to a discrete problem. In principle, it is the equivalent of applying the method of variation of parameters to a function space, by converting the equation to a...
- Interval finite elementInterval finite elementThe interval finite element method is a finite element method that uses interval parameters. Interval FEM can be applied in situations where it is not possible to get reliable probabilistic characteristics of the structure. This is important in concrete structures, wood structures, geomechanics,...
- Isogeometric analysisIsogeometric AnalysisIsogeometric analysis is a recently developed computational approach that offers the possibility of integrating finite element analysis into conventional NURBS-based CAD design tools. Currently, it is necessary to convert data between CAD and FEA packages to analyse new designs during development,...
- List of finite element software packages
- Movable Cellular Automata
- Multidisciplinary design optimizationMultidisciplinary design optimizationMulti-disciplinary design optimization is a field of engineering that uses optimization methods to solve design problems incorporating a number of disciplines. As defined by Prof. Carlo Poloni, MDO is "the art of finding the best compromise"...
- MultiphysicsMultiphysicsMultiphysics treats simulations that involve multiple physical models or multiple simultaneous physical phenomena. For example, combining chemical kinetics and fluid mechanics or combining finite elements with molecular dynamics...
- Patch testPatch test (finite elements)The patch test in the finite element method is a simple indicator of the quality of a finite element, developed by Bruce Irons.The patch test uses a partial differential equation on a domain consisting from several elements set up so that the exact solution is known...
- Rayleigh-Ritz methodRayleigh-Ritz methodIn applied mathematics and mechanical engineering, the Rayleigh–Ritz method is a widely used, classical method for the calculation of the natural vibration frequency of a structure in the second or higher order...
- Weakened weak formWeakened weak formWeakened weak form is used in the formulation of general numerical methods based on meshfree methods and/or finite element method settings. These numerical methods are applicable to solid mechanics as well as fluid dynamics problems....
External links
- NAFEMS -- The International Association for the Engineering Analysis Community
- Finite Element Analysis Resources- Finite Element news, articles and tips
- Finite-element Methods for Electromagnetics - free 320-page text
- Finite Element Books- books bibliography
- Mathematics of the Finite Element Method
- Finite Element Methods for Partial Differential Equations - Lecture notes by Endre SüliEndre SüliEndre Süli is Professor of Numerical Analysis in the Mathematical Institute, University of Oxford, Fellow and Tutor in Mathematics at Worcester College, Oxford, and Supernumerary Fellow of Linacre College, Oxford...
- Electromagnetic Modeling web site at Clemson University (includes list of currently available software)