
Plane wave
Encyclopedia
In the physics
of wave propagation
, a plane wave (also spelled planewave) is a constant-frequency wave whose wavefront
s (surfaces of constant phase
) are infinite parallel planes of constant peak-to-peak amplitude
normal to the phase velocity
vector.
It is not possible in practice to have a true plane wave; only a plane wave of infinite extent will propagate as a plane wave. However, many waves
are approximately plane waves in a localized region of space. For example, a localized source such as an antenna produces a field that is approximately a plane wave far from the antenna in its far-field region. Similarly, if the length scale
s are much longer than the wave’s wavelength, as is often the case for light in the field of optics
, one can treat the waves as light rays
which correspond locally to plane waves.
and cosine functions. One of the simplest ways to use such a sinusoid involves defining it along the direction of the x-axis
. The below equation, which is illustrated toward the right, uses the cosine function to represent a plane wave travelling in the positive x direction.
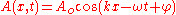
In the above equation…
Other formalisms which directly use the wave’s wavelength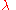 , period
, period  , frequency
, frequency
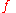 and velocity
and velocity
 are below.
are below.
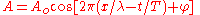
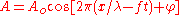
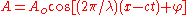
To appreciate the equivalence of the above set of equations note that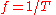 and
and 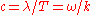
A more generalized form is used to describe a plane wave traveling in an arbitrary direction. It uses vectors in combination with the vector dot product
.

here:
Many choose to use a more mathematically versatile formulation that utilizes the complex number plane
. It requires the use of the natural exponent
 and the imaginary number
and the imaginary number
.
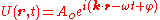
To appreciate this equation’s relationship to the earlier ones, below is this same equation expressed using sines and cosines. Observe that the first term equals the real form of the plane wave just discussed.


The complex form of the plane wave just introduced can be simplified by using a complex valued
amplitude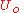 in place of the real valued
in place of the real valued
amplitude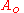 .
.
Specifically, since the complex form…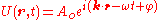
equals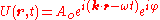
one can absorb the phase factor
into a complex amplitude by letting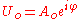 , resulting in the more compact equation
, resulting in the more compact equation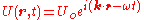
While the complex form has an imaginary component, after the necessary calculations are performed in the complex plane, its real value can be extracted giving a real valued equation representing an actual plane wave.
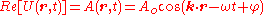
The main reason one would choose to work with the complex exponential form of the plane wave is because complex exponentials are often algebraically
easier to work with than the trigonometric
sines and cosines. Specifically, the angle-addition rules are much simpler for complex exponentials.
Additionally, when using Fourier analysis techniques for waves in a lossy medium, the resulting attenuation
is easier to deal with using complex Fourier coefficients. It should be noted however that if a wave is traveling through a lossy medium, the amplitude of the wave is no longer constant and therefore the wave is strictly speaking is no longer a true plane wave.
In quantum mechanics
the solutions of the Schrödinger wave equation are by their very nature complex and in the simplest instance take a form identical to the complex plane wave representation above. The imaginary component in that instance however has not been introduced for the purpose of mathematical expediency but is in fact an inherent part of the “wave”.
These waves are solutions for a scalar
wave equation
in a homogeneous medium. For vector wave equations, such as the ones describing electromagnetic radiation
or waves in an elastic solid, the solution for a homogeneous medium is similar: the scalar amplitude Ao is replaced by a constant vector Ao. For example, in electromagnetism
Ao is typically the vector for the electric field
, magnetic field
, or vector potential
. A transverse wave
is one in which the amplitude vector is orthogonal to k, which is the case for electromagnetic waves in an isotropic medium. By contrast, a longitudinal wave
is one in which the amplitude vector is parallel to k, such as for acoustic waves in a gas or fluid.
The plane-wave equation works for arbitrary combinations of ω and k, but any real physical medium will only allow such waves to propagate for those combinations of ω and k that satisfy the dispersion relation
of the medium. The dispersion relation is often expressed as a function, ω(k). The ratio ω/|k| gives the magnitude of the phase velocity
and dω/dk gives the group velocity
. For electromagnetism in an isotropic medium with index of refraction n, the phase velocity is c/n, which equals the group velocity if the index is not frequency-dependent.
In linear uniform media, a wave solution can be expressed as a superposition of plane waves. This approach is known as the Angular spectrum method
. The form of the planewave solution is actually a general consequence of translational symmetry
. More generally, for periodic structures having discrete translational symmetry, the solutions take the form of Bloch wave
s, most famously in crystal
line atomic materials but also in photonic crystal
s and other periodic wave equations. As another generalization, for structures that are only uniform along one direction x (such as a waveguide
along the x direction), the solutions (waveguide modes) are of the form exp[i(kx-ωt)] multiplied by some amplitude function a(y,z). This is a special case of a separable partial differential equation
.
The term is used in the same way for telecommunication
, e.g. in Federal Standard 1037C
and MIL-STD-188
.
, electromagnetic wave. Because this is a plane wave, each blue vector, indicating the perpendicular displacement from a point on the axis out to the sine wave, represents the magnitude and direction of the electric field
for an entire plane that is perpendicular to the axis.
Represented in the second illustration is a circularly polarized
, electromagnetic plane wave. Each blue vector indicating the perpendicular displacement from a point on the axis out to the helix, also represents the magnitude and direction of the electric field for an entire plane perpendicular to the axis.
In both illustrations, along the axes is a series of shorter blue vectors which are scaled down versions of the longer blue vectors. These shorter blue vectors are extrapolated out into the block of black vectors which fill a volume of space. Notice that for a given plane, the black vectors are identical, indicating that the magnitude and direction of the electric field is constant along that plane.
In the case of the linearly polarized light, the field strength from plane to plane varies from a maximum in one direction, down to zero, and then back up to a maximum in the opposite direction.
In the case of the circularly polarized light, the field strength remains constant from plane to plane but its direction steadily changes in a rotary type manner.
Not indicated in either illustration is the electric field’s corresponding magnetic field
which is proportional in strength to the electric field at each point in space but is at a right angle to it. Illustrations of the magnetic field vectors would be virtually identical to these except all the vectors would be rotated 90 degrees perpendicular to the direction of propagation.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
of wave propagation
Wave propagation
Wave propagation is any of the ways in which waves travel.With respect to the direction of the oscillation relative to the propagation direction, we can distinguish between longitudinal wave and transverse waves....
, a plane wave (also spelled planewave) is a constant-frequency wave whose wavefront
Wavefront
In physics, a wavefront is the locus of points having the same phase. Since infrared, optical, x-ray and gamma-ray frequencies are so high, the temporal component of electromagnetic waves is usually ignored at these wavelengths, and it is only the phase of the spatial oscillation that is described...
s (surfaces of constant phase
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
) are infinite parallel planes of constant peak-to-peak amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
normal to the phase velocity
Phase velocity
The phase velocity of a wave is the rate at which the phase of the wave propagates in space. This is the speed at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave will appear to travel at the phase velocity...
vector.
It is not possible in practice to have a true plane wave; only a plane wave of infinite extent will propagate as a plane wave. However, many waves
WAVES
The WAVES were a World War II-era division of the U.S. Navy that consisted entirely of women. The name of this group is an acronym for "Women Accepted for Volunteer Emergency Service" ; the word "emergency" implied that the acceptance of women was due to the unusual circumstances of the war and...
are approximately plane waves in a localized region of space. For example, a localized source such as an antenna produces a field that is approximately a plane wave far from the antenna in its far-field region. Similarly, if the length scale
Length scale
In physics, length scale is a particular length or distance determined with the precision of one order of magnitude. The concept of length scale is particularly important because physical phenomena of different length scales cannot affect each other and are said to decouple...
s are much longer than the wave’s wavelength, as is often the case for light in the field of optics
Optics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
, one can treat the waves as light rays
Geometrical optics
Geometrical optics, or ray optics, describes light propagation in terms of "rays". The "ray" in geometric optics is an abstraction, or "instrument", which can be used to approximately model how light will propagate. Light rays are defined to propagate in a rectilinear path as far as they travel in...
which correspond locally to plane waves.
Mathematical formalisms
Two functions that meet the above criteria of having a constant frequency and constant amplitude are the sineSine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
and cosine functions. One of the simplest ways to use such a sinusoid involves defining it along the direction of the x-axis
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
. The below equation, which is illustrated toward the right, uses the cosine function to represent a plane wave travelling in the positive x direction.
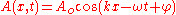
In the above equation…
-
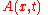 is the magnitude or disturbance of the wave at a given point in space and time. An example would be to let
is the magnitude or disturbance of the wave at a given point in space and time. An example would be to let 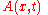 represent the variation of air pressure relative to the norm in the case of a sound wave.
represent the variation of air pressure relative to the norm in the case of a sound wave. -
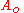 is the amplitudeAmplitudeAmplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
is the amplitudeAmplitudeAmplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
of the wave which is the peak magnitude of the oscillation. - is the wave’s wave number or more specifically the angular wave number and equals , where is the wavelengthWavelengthIn physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
of the wave. has the units of radianRadianRadian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s per unit distance and is a measure of how rapidly the disturbance changes over a given distance at a particular point in time. -
 is a point along the x-axis.
is a point along the x-axis. 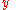 and
and  are not part of the equation because the wave's magnitude and phase are the same at every point on any given planePlane-Physical objects:* Aeroplane or airplane, a fixed-wing aircraft* Plane , a woodworking tool to smooth surfaces* Platanus, a genus of trees with the common name "plane"* Acer pseudoplatanus, a tree species sometimes called "plane"...
are not part of the equation because the wave's magnitude and phase are the same at every point on any given planePlane-Physical objects:* Aeroplane or airplane, a fixed-wing aircraft* Plane , a woodworking tool to smooth surfaces* Platanus, a genus of trees with the common name "plane"* Acer pseudoplatanus, a tree species sometimes called "plane"...
. This equation defines what that magnitude and phase are. -
 is the wave’s angular frequencyAngular frequencyIn physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
is the wave’s angular frequencyAngular frequencyIn physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
which equals , where is the period of the wave. has the units of radians per unit time and is a measure of how rapidly the disturbance changes over a given length of time at a particular point in space.
has the units of radians per unit time and is a measure of how rapidly the disturbance changes over a given length of time at a particular point in space. -
 is a given point in time
is a given point in time -
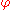 is the phase shift of the wave and has the units of radians. Note that a positive phase shift, at a given moment of time, shifts the wave in the negative x-axis direction. A phase shift of radians shifts it exactly one wavelength.
is the phase shift of the wave and has the units of radians. Note that a positive phase shift, at a given moment of time, shifts the wave in the negative x-axis direction. A phase shift of radians shifts it exactly one wavelength.
Other formalisms which directly use the wave’s wavelength
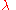 , period
, period  , frequency
, frequencyFrequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
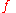 and velocity
and velocityVelocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
 are below.
are below.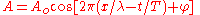
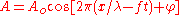
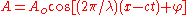
To appreciate the equivalence of the above set of equations note that
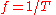 and
and 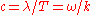
A more generalized form is used to describe a plane wave traveling in an arbitrary direction. It uses vectors in combination with the vector dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
.

here:
- is the wave vectorWave vectorIn physics, a wave vector is a vector which helps describe a wave. Like any vector, it has a magnitude and direction, both of which are important: Its magnitude is either the wavenumber or angular wavenumber of the wave , and its direction is ordinarily the direction of wave propagation In...
which only differs from a wave number in that it has a direction as well as a magnitude. This means that,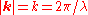 . The direction of the wave vector is ordinarily the direction that the plane wave is traveling, but it can differ slightly in an anisotropic mediumAnisotropyAnisotropy is the property of being directionally dependent, as opposed to isotropy, which implies identical properties in all directions. It can be defined as a difference, when measured along different axes, in a material's physical or mechanical properties An example of anisotropy is the light...
. The direction of the wave vector is ordinarily the direction that the plane wave is traveling, but it can differ slightly in an anisotropic mediumAnisotropyAnisotropy is the property of being directionally dependent, as opposed to isotropy, which implies identical properties in all directions. It can be defined as a difference, when measured along different axes, in a material's physical or mechanical properties An example of anisotropy is the light...
.  is the vector dot productDot productIn mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
is the vector dot productDot productIn mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
. is the position vector which defines a point in three-dimensional space.
is the position vector which defines a point in three-dimensional space.
Many choose to use a more mathematically versatile formulation that utilizes the complex number plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
. It requires the use of the natural exponent
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
 and the imaginary number
and the imaginary numberImaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
.
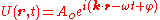
To appreciate this equation’s relationship to the earlier ones, below is this same equation expressed using sines and cosines. Observe that the first term equals the real form of the plane wave just discussed.


The complex form of the plane wave just introduced can be simplified by using a complex valued
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
amplitude
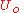 in place of the real valued
in place of the real valuedReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
amplitude
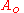 .
. Specifically, since the complex form…
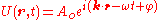
equals
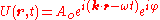
one can absorb the phase factor
Phase factor
For any complex number written in polar form , the phase factor is the exponential part, i.e. eiθ. As such, the term "phase factor" is similar to the term phasor, although the former term is more common in quantum mechanics. This phase factor is itself a complex number of absolute value 1...
into a complex amplitude by letting
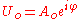 , resulting in the more compact equation
, resulting in the more compact equation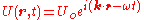
While the complex form has an imaginary component, after the necessary calculations are performed in the complex plane, its real value can be extracted giving a real valued equation representing an actual plane wave.
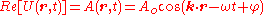
The main reason one would choose to work with the complex exponential form of the plane wave is because complex exponentials are often algebraically
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
easier to work with than the trigonometric
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
sines and cosines. Specifically, the angle-addition rules are much simpler for complex exponentials.
Additionally, when using Fourier analysis techniques for waves in a lossy medium, the resulting attenuation
Attenuation
In physics, attenuation is the gradual loss in intensity of any kind of flux through a medium. For instance, sunlight is attenuated by dark glasses, X-rays are attenuated by lead, and light and sound are attenuated by water.In electrical engineering and telecommunications, attenuation affects the...
is easier to deal with using complex Fourier coefficients. It should be noted however that if a wave is traveling through a lossy medium, the amplitude of the wave is no longer constant and therefore the wave is strictly speaking is no longer a true plane wave.
In quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
the solutions of the Schrödinger wave equation are by their very nature complex and in the simplest instance take a form identical to the complex plane wave representation above. The imaginary component in that instance however has not been introduced for the purpose of mathematical expediency but is in fact an inherent part of the “wave”.
These waves are solutions for a scalar
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
in a homogeneous medium. For vector wave equations, such as the ones describing electromagnetic radiation
Electromagnetic radiation
Electromagnetic radiation is a form of energy that exhibits wave-like behavior as it travels through space...
or waves in an elastic solid, the solution for a homogeneous medium is similar: the scalar amplitude Ao is replaced by a constant vector Ao. For example, in electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
Ao is typically the vector for the electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
, magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
, or vector potential
Vector potential
In vector calculus, a vector potential is a vector field whose curl is a given vector field. This is analogous to a scalar potential, which is a scalar field whose negative gradient is a given vector field....
. A transverse wave
Transverse wave
A transverse wave is a moving wave that consists of oscillations occurring perpendicular to the direction of energy transfer...
is one in which the amplitude vector is orthogonal to k, which is the case for electromagnetic waves in an isotropic medium. By contrast, a longitudinal wave
Longitudinal wave
Longitudinal waves, as known as "l-waves", are waves that have the same direction of vibration as their direction of travel, which means that the movement of the medium is in the same direction as or the opposite direction to the motion of the wave. Mechanical longitudinal waves have been also...
is one in which the amplitude vector is parallel to k, such as for acoustic waves in a gas or fluid.
The plane-wave equation works for arbitrary combinations of ω and k, but any real physical medium will only allow such waves to propagate for those combinations of ω and k that satisfy the dispersion relation
Dispersion relation
In physics and electrical engineering, dispersion most often refers to frequency-dependent effects in wave propagation. Note, however, that there are several other uses of the word "dispersion" in the physical sciences....
of the medium. The dispersion relation is often expressed as a function, ω(k). The ratio ω/|k| gives the magnitude of the phase velocity
Phase velocity
The phase velocity of a wave is the rate at which the phase of the wave propagates in space. This is the speed at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave will appear to travel at the phase velocity...
and dω/dk gives the group velocity
Group velocity
The group velocity of a wave is the velocity with which the overall shape of the wave's amplitudes — known as the modulation or envelope of the wave — propagates through space....
. For electromagnetism in an isotropic medium with index of refraction n, the phase velocity is c/n, which equals the group velocity if the index is not frequency-dependent.
In linear uniform media, a wave solution can be expressed as a superposition of plane waves. This approach is known as the Angular spectrum method
Angular spectrum method
The angular spectrum method is a technique for modeling the propagation of a wave field. This technique involves expanding a complex wave field into a summation of infinite number of plane waves. Its mathematical origins lie in the field of Fourier Optics but it has been applied extensively in the...
. The form of the planewave solution is actually a general consequence of translational symmetry
Translational symmetry
In geometry, a translation "slides" an object by a a: Ta = p + a.In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation...
. More generally, for periodic structures having discrete translational symmetry, the solutions take the form of Bloch wave
Bloch wave
A Bloch wave or Bloch state, named after Felix Bloch, is the wavefunction of a particle placed in a periodic potential...
s, most famously in crystal
Crystal
A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
line atomic materials but also in photonic crystal
Photonic crystal
Photonic crystals are periodic optical nanostructures that are designed to affect the motion of photons in a similar way that periodicity of a semiconductor crystal affects the motion of electrons...
s and other periodic wave equations. As another generalization, for structures that are only uniform along one direction x (such as a waveguide
Waveguide
A waveguide is a structure which guides waves, such as electromagnetic waves or sound waves. There are different types of waveguides for each type of wave...
along the x direction), the solutions (waveguide modes) are of the form exp[i(kx-ωt)] multiplied by some amplitude function a(y,z). This is a special case of a separable partial differential equation
Separable partial differential equation
A separable partial differential equation is one that can be broken into a set of separate equations of lower dimensionality by a method of separation of variables. This generally relies upon the problem having some special form or symmetry...
.
The term is used in the same way for telecommunication
Telecommunication
Telecommunication is the transmission of information over significant distances to communicate. In earlier times, telecommunications involved the use of visual signals, such as beacons, smoke signals, semaphore telegraphs, signal flags, and optical heliographs, or audio messages via coded...
, e.g. in Federal Standard 1037C
Federal Standard 1037C
Federal Standard 1037C, titled Telecommunications: Glossary of Telecommunication Terms is a United States Federal Standard, issued by the General Services Administration pursuant to the Federal Property and Administrative Services Act of 1949, as amended....
and MIL-STD-188
MIL-STD-188
MIL-STD-188 is a series of U.S. military standards relating to telecommunications.-Purpose:Faced with “past technical deficiencies in telecommunications systems and equipment and software…that were traced to basic inadequacies in the application of telecommunication standards and to the lack of a...
.
Polarized electromagnetic plane waves
Represented in the first illustration toward the right is a linearly polarizedLinear polarization
In electrodynamics, linear polarization or plane polarization of electromagnetic radiation is a confinement of the electric field vector or magnetic field vector to a given plane along the direction of propagation...
, electromagnetic wave. Because this is a plane wave, each blue vector, indicating the perpendicular displacement from a point on the axis out to the sine wave, represents the magnitude and direction of the electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
for an entire plane that is perpendicular to the axis.
Represented in the second illustration is a circularly polarized
Circular polarization
In electrodynamics, circular polarization of an electromagnetic wave is a polarization in which the electric field of the passing wave does not change strength but only changes direction in a rotary type manner....
, electromagnetic plane wave. Each blue vector indicating the perpendicular displacement from a point on the axis out to the helix, also represents the magnitude and direction of the electric field for an entire plane perpendicular to the axis.
In both illustrations, along the axes is a series of shorter blue vectors which are scaled down versions of the longer blue vectors. These shorter blue vectors are extrapolated out into the block of black vectors which fill a volume of space. Notice that for a given plane, the black vectors are identical, indicating that the magnitude and direction of the electric field is constant along that plane.
In the case of the linearly polarized light, the field strength from plane to plane varies from a maximum in one direction, down to zero, and then back up to a maximum in the opposite direction.
In the case of the circularly polarized light, the field strength remains constant from plane to plane but its direction steadily changes in a rotary type manner.
Not indicated in either illustration is the electric field’s corresponding magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
which is proportional in strength to the electric field at each point in space but is at a right angle to it. Illustrations of the magnetic field vectors would be virtually identical to these except all the vectors would be rotated 90 degrees perpendicular to the direction of propagation.
See also
- Angular spectrum methodAngular spectrum methodThe angular spectrum method is a technique for modeling the propagation of a wave field. This technique involves expanding a complex wave field into a summation of infinite number of plane waves. Its mathematical origins lie in the field of Fourier Optics but it has been applied extensively in the...
- Plane waves in a vacuum
- Plane wave expansion

