
Effective Medium Approximations
Encyclopedia
Effective medium approximations or effective medium theory (sometimes abbreviated as EMA or EMT) are physical models that describe the macroscopic properties of a medium based on the properties and the relative fractions of its components. They can be discrete models such as applied to resistor networks or continuum theories as applied to elasticity or viscosity but most of the current theories have difficulty in describing percolating systems. Indeed, among the numerous effective medium approximations, only Bruggeman’s symmetrical theory is able to predict a threshold. This characteristic feature of the latter theory puts it in the same category as other mean field theories of critical phenomena
.
There are many different effective medium approximations, each of them being more or less accurate in distinct conditions. Nevertheless, they all assume that the macroscopic system is homogeneous and typical of all mean field theories, they fail to predict the properties of a multiphase medium close to the percolation threshold due to the absence of long-range correlations or critical fluctuations in the theory.
The properties under consideration are usually the conductivity or the dielectric constant
or the dielectric constant
 of the medium. These parameters are interchangeable in the formulas in a whole range of models due to the wide applicability of the Laplace equation. The problems that fall outside of this class are mainly in the field of elasticity and hydrodynamics, due to the higher order tensorial character of the effective medium constants.
of the medium. These parameters are interchangeable in the formulas in a whole range of models due to the wide applicability of the Laplace equation. The problems that fall outside of this class are mainly in the field of elasticity and hydrodynamics, due to the higher order tensorial character of the effective medium constants.
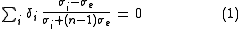
In a system of Euclidean spatial dimension that has an arbitrary number of components, the sum is made over all the constituents.
that has an arbitrary number of components, the sum is made over all the constituents.  and
and 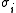 are respectively the fraction and the conductivity of each component, and
are respectively the fraction and the conductivity of each component, and 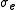 is the effective conductivity of the medium. (The sum over the
is the effective conductivity of the medium. (The sum over the 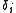 's is unity.)
's is unity.)
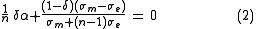
This is a generalization of Eq. (1) to a biphasic system with ellipsoidal inclusions of conductivity into a matrix of conductivity
into a matrix of conductivity 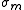 . The fraction of inclusions is
. The fraction of inclusions is 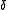 and the system is
and the system is  dimensional. For randomly oriented inclusions,
dimensional. For randomly oriented inclusions,

where the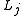 's denote the appropriate doublet/triplet of depolarization factors which is governed by the ratios between the axis of the ellipse/ellipsoid. For example: in the case of a circle {
's denote the appropriate doublet/triplet of depolarization factors which is governed by the ratios between the axis of the ellipse/ellipsoid. For example: in the case of a circle { ,
, 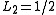 } and in the case of a sphere {
} and in the case of a sphere {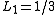 ,
, 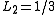 ,
, 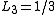 }. (The sum over the
}. (The sum over the  's is unity.)
's is unity.)
The most general case to which the Bruggeman approach has been applied involves bianisotropic ellipsoidal inclusions.
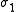 , take it as a sphere of volume
, take it as a sphere of volume 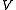 and assume it is embedded in a uniform medium with an effective conductivity
and assume it is embedded in a uniform medium with an effective conductivity 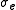 . If the electric field
. If the electric field
far from the inclusion is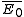 then elementary considerations lead to a dipole moment
then elementary considerations lead to a dipole moment
associated with the volume

This polarization
produces a deviation from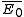 . If the average deviation is to vanish, the total polarization summed over the two types of inclusion must vanish. Thus
. If the average deviation is to vanish, the total polarization summed over the two types of inclusion must vanish. Thus
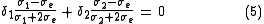
where and
and 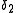 are respectively the volume fraction of material 1 and 2. This can be easily extended to a system of dimension
are respectively the volume fraction of material 1 and 2. This can be easily extended to a system of dimension  that has an arbitrary number of components. All cases
that has an arbitrary number of components. All cases
can be combined to yield Eq. (1).
Eq. (1) can also be obtained by requiring the deviation in current to vanish
. It has been derived here from the assumption that the inclusions are spherical and it can be modified for shapes with other depolarization factors; leading to Eq. (2).
A more general derivation applicable to bianisotropic materials is also available.
Unfortunately, it is not the case close to the percolation threshold where the system is governed by the largest cluster of conductors, which is a fractal, and long-range correlations that are totally absent from Bruggeman's simple formula.
The threshold values are in general not correctly predicted. It is 33% in the EMA, in three dimensions, far
from the 16% expected from percolation theory and observed in experiments. However, in
two dimensions, the EMA gives a threshold of 50% and has been proven to model percolation
relatively well
.
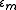 and inclusions with
and inclusions with 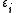 .
.
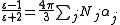
By using elementary electrostatic, we get for a spherical inclusion with dielectric constant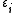 and a radius
and a radius  a polarisability
a polarisability  :
: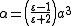
If we combine with the Clausius Mosotti eqation, we get:
with the Clausius Mosotti eqation, we get:
Where is the effective dielectric constant of the medium,
is the effective dielectric constant of the medium, 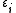 is the one of the inclusions;
is the one of the inclusions; 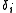 is the volume fraction of the inclusions.
is the volume fraction of the inclusions.
As the model of Maxwell Garnett is a Composition of a matrix medium with inclusions we enhance the equation:

This is the Maxwell Garnett equation.
Where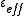 is the effective dielectric constant of the medium,
is the effective dielectric constant of the medium, 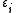 is the one of the inclusions and
is the one of the inclusions and 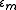 is the one of the matrix;
is the one of the matrix; 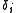 is the volume fraction of the inclusions.
is the volume fraction of the inclusions.
Only if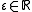 we can simplify the Maxwell Garnett equation to:
we can simplify the Maxwell Garnett equation to: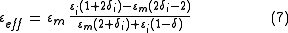
where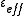 is the effective dielectric constant of the medium,
is the effective dielectric constant of the medium, 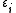 is the one of the inclusions and
is the one of the inclusions and  is the one of the matrix;
is the one of the matrix;  is the volume fraction of the embedded material.
is the volume fraction of the embedded material.
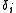 since it is assumed that the domains are spatially separated
since it is assumed that the domains are spatially separated
.
Critical phenomena
In physics, critical phenomena is the collective name associated with thephysics of critical points. Most of them stem from the divergence of thecorrelation length, but also the dynamics slows down...
.
There are many different effective medium approximations, each of them being more or less accurate in distinct conditions. Nevertheless, they all assume that the macroscopic system is homogeneous and typical of all mean field theories, they fail to predict the properties of a multiphase medium close to the percolation threshold due to the absence of long-range correlations or critical fluctuations in the theory.
The properties under consideration are usually the conductivity
 or the dielectric constant
or the dielectric constantDielectric constant
The relative permittivity of a material under given conditions reflects the extent to which it concentrates electrostatic lines of flux. In technical terms, it is the ratio of the amount of electrical energy stored in a material by an applied voltage, relative to that stored in a vacuum...
 of the medium. These parameters are interchangeable in the formulas in a whole range of models due to the wide applicability of the Laplace equation. The problems that fall outside of this class are mainly in the field of elasticity and hydrodynamics, due to the higher order tensorial character of the effective medium constants.
of the medium. These parameters are interchangeable in the formulas in a whole range of models due to the wide applicability of the Laplace equation. The problems that fall outside of this class are mainly in the field of elasticity and hydrodynamics, due to the higher order tensorial character of the effective medium constants.Formulas
Without any loss of generality, we shall consider the study of the effective conductivity (which can be either dc or ac) for a system made up of spherical multicomponent inclusions with different arbitrary conductivities. Then the celebrated Bruggeman formula takes the form:Circular and spherical inclusions
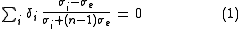
In a system of Euclidean spatial dimension
 that has an arbitrary number of components, the sum is made over all the constituents.
that has an arbitrary number of components, the sum is made over all the constituents.  and
and 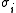 are respectively the fraction and the conductivity of each component, and
are respectively the fraction and the conductivity of each component, and 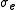 is the effective conductivity of the medium. (The sum over the
is the effective conductivity of the medium. (The sum over the 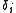 's is unity.)
's is unity.)Elliptical and ellipsoidal inclusions
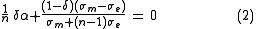
This is a generalization of Eq. (1) to a biphasic system with ellipsoidal inclusions of conductivity
 into a matrix of conductivity
into a matrix of conductivity 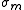 . The fraction of inclusions is
. The fraction of inclusions is 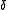 and the system is
and the system is  dimensional. For randomly oriented inclusions,
dimensional. For randomly oriented inclusions,
where the
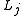 's denote the appropriate doublet/triplet of depolarization factors which is governed by the ratios between the axis of the ellipse/ellipsoid. For example: in the case of a circle {
's denote the appropriate doublet/triplet of depolarization factors which is governed by the ratios between the axis of the ellipse/ellipsoid. For example: in the case of a circle { ,
, 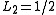 } and in the case of a sphere {
} and in the case of a sphere {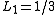 ,
, 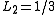 ,
, 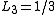 }. (The sum over the
}. (The sum over the  's is unity.)
's is unity.)The most general case to which the Bruggeman approach has been applied involves bianisotropic ellipsoidal inclusions.
Derivation
The figure illustrates a two-component medium. Let us consider the cross-hatched volume of conductivity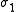 , take it as a sphere of volume
, take it as a sphere of volume 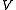 and assume it is embedded in a uniform medium with an effective conductivity
and assume it is embedded in a uniform medium with an effective conductivity 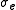 . If the electric field
. If the electric fieldElectric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
far from the inclusion is
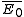 then elementary considerations lead to a dipole moment
then elementary considerations lead to a dipole momentDipole moment
Dipole moment can be defined as the product of magnitude of charge & distance of separation between the charges.Dipole moment may refer to:*Electric dipole moment, the measure of the electrical polarity of a system of charges...
associated with the volume

This polarization
Polarization
Polarization is a property of certain types of waves that describes the orientation of their oscillations. Electromagnetic waves, such as light, and gravitational waves exhibit polarization; acoustic waves in a gas or liquid do not have polarization because the direction of vibration and...
produces a deviation from
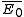 . If the average deviation is to vanish, the total polarization summed over the two types of inclusion must vanish. Thus
. If the average deviation is to vanish, the total polarization summed over the two types of inclusion must vanish. Thus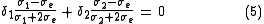
where
 and
and 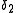 are respectively the volume fraction of material 1 and 2. This can be easily extended to a system of dimension
are respectively the volume fraction of material 1 and 2. This can be easily extended to a system of dimension  that has an arbitrary number of components. All cases
that has an arbitrary number of components. All casescan be combined to yield Eq. (1).
Eq. (1) can also be obtained by requiring the deviation in current to vanish
. It has been derived here from the assumption that the inclusions are spherical and it can be modified for shapes with other depolarization factors; leading to Eq. (2).
A more general derivation applicable to bianisotropic materials is also available.
Modeling of percolating systems
The main approximation is that all the domains are located in an equivalent mean field.Unfortunately, it is not the case close to the percolation threshold where the system is governed by the largest cluster of conductors, which is a fractal, and long-range correlations that are totally absent from Bruggeman's simple formula.
The threshold values are in general not correctly predicted. It is 33% in the EMA, in three dimensions, far
from the 16% expected from percolation theory and observed in experiments. However, in
two dimensions, the EMA gives a threshold of 50% and has been proven to model percolation
relatively well
.
Maxwell Garnett's Equation
In the Maxwell Garnett Approximation the effective medium consists of a matrix medium with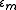 and inclusions with
and inclusions with 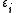 .
.Derivation
For the derivation of the Maxwell-Garnett equation we start with an array of polarizable particles. Only by using the Lorentz local field concept, it is straightforward to get the Clausius Mosotti equation.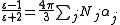
By using elementary electrostatic, we get for a spherical inclusion with dielectric constant
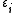 and a radius
and a radius  a polarisability
a polarisability  :
: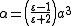
If we combine
 with the Clausius Mosotti eqation, we get:
with the Clausius Mosotti eqation, we get:
Where
 is the effective dielectric constant of the medium,
is the effective dielectric constant of the medium, 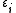 is the one of the inclusions;
is the one of the inclusions; 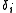 is the volume fraction of the inclusions.
is the volume fraction of the inclusions.As the model of Maxwell Garnett is a Composition of a matrix medium with inclusions we enhance the equation:
Formula

This is the Maxwell Garnett equation.
Where
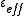 is the effective dielectric constant of the medium,
is the effective dielectric constant of the medium, 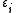 is the one of the inclusions and
is the one of the inclusions and 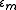 is the one of the matrix;
is the one of the matrix; 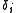 is the volume fraction of the inclusions.
is the volume fraction of the inclusions.Only if
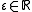 we can simplify the Maxwell Garnett equation to:
we can simplify the Maxwell Garnett equation to: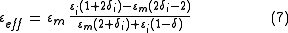
where
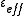 is the effective dielectric constant of the medium,
is the effective dielectric constant of the medium, 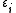 is the one of the inclusions and
is the one of the inclusions and  is the one of the matrix;
is the one of the matrix;  is the volume fraction of the embedded material.
is the volume fraction of the embedded material.Validity
In general terms, the Maxwell Garnett EMA is expected to be valid at low volume fractions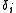 since it is assumed that the domains are spatially separated
since it is assumed that the domains are spatially separated.

