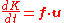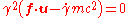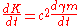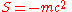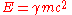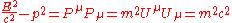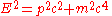Four-vector
Encyclopedia
In the theory of relativity
, a four-vector is a vector in a four-dimensional real vector space
, called Minkowski space
. It differs from a vector in that it can be transformed by Lorentz transformations. The usage of the four-vector name tacitly assumes that its components refer to a standard basis. The components transform between these bases as the space
and time
coordinate differences, under spatial translations, rotations, and boosts (a change by a constant velocity to another inertial reference frame). The set of all such translations, rotations, and boosts (called Poincaré transformations) forms the Poincaré group
under spatial translations, rotations, and boosts (a change by a constant velocity to another inertial reference frame). The set of all such translations, rotations, and boosts (called Poincaré transformations) forms the Poincaré group
. The set of rotations and boosts (Lorentz transformation
s, described by 4×4 matrices
) forms the Lorentz group
.
This article considers four-vectors in the context of special relativity
. Although the concept of four-vectors also extends to general relativity
, some of the results stated in this article require modification in general relativity.
is called an "event" and is described in a standard basis by a set of four coordinates such as

where = 0, 1, 2, 3, labels the spacetime
= 0, 1, 2, 3, labels the spacetime
dimension
s and where c is the speed of light
. The definition ensures that all the coordinates have the same units (of distance). These coordinates are the components of the position four-vector for the event.
ensures that all the coordinates have the same units (of distance). These coordinates are the components of the position four-vector for the event.
The displacement four-vector is defined to be an "arrow" linking two events:
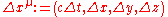
(Note that the position vector is the displacement vector when one of the two events is the origin of the coordinate system. Position vectors are relatively trivial; the general theory of four-vectors is concerned with displacement vectors.)
The scalar product of two four-vectors and
and  is defined (using Einstein notation
is defined (using Einstein notation
) as

where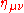 is the entry in the
is the entry in the  th row and
th row and  th column of the Minkowski metric
th column of the Minkowski metric  . Sometimes this inner product is called the Minkowski inner product. It is not a true inner product in the mathematical sense because it is not positive definite. (Note: some authors define
. Sometimes this inner product is called the Minkowski inner product. It is not a true inner product in the mathematical sense because it is not positive definite. (Note: some authors define  with the opposite sign:
with the opposite sign: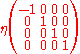
in which case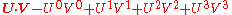
Either convention will work, since the primary significance of the Minkowski inner product is that for any two four-vectors, its value is invariant for all observers.)
An important property of the inner product is that it is invariant
(that is, a scalar
): a change of coordinates does not result in a change in value of the inner product.
The inner product is often expressed as the effect of the dual vector of one vector on the other:

Here the s are the components of the dual vector
s are the components of the dual vector 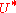 of
of  in the dual basis and called the covariant coordinates of
in the dual basis and called the covariant coordinates of  , while the original
, while the original 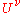 components are called the contravariant coordinates. Lower and upper indices indicate always covariant and contravariant coordinates, respectively.
components are called the contravariant coordinates. Lower and upper indices indicate always covariant and contravariant coordinates, respectively.
The relation between the covariant and contravariant coordinates is:
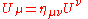 .
.
The four-vectors are arrows on the spacetime diagram or Minkowski diagram
. In this article, four-vectors will be referred to simply as vectors.
Four-vectors may be classified as either spacelike, timelike or null. Spacelike, timelike, and null vectors are ones whose inner product with themselves is less than, greater than, and equal to zero respectively (assuming Minkowski metric with signature
(+,-,-,-)).
In special relativity (but not general relativity), the derivative of a four-vector with respect to a scalar (invariant) is itself a four-vector.
(τ). As proper time is an invariant, this guarantees that the proper-time-derivative of any four-vector is itself a four-vector. It is then important to find a relation between this proper-time-derivative and another time derivative (using the time of an inertial reference frame). This relation is provided by the time transformation in the Lorentz transformations and is:
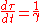
where γ is the Lorentz factor
. Important four-vectors in relativity theory can now be defined.
of an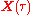 world line
world line
is defined by:
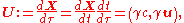
where, using suffix notation,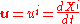
for . Notice that
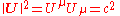
The geometric meaning of 4-velocity is the unit vector tangent to the world line in Minkowski space.
is given by:
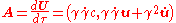
Since the magnitude of
of  is a constant, the four acceleration is (pseudo-)orthogonal to the four velocity, i.e. the Minkowski inner product of the four-acceleration and the four-velocity is zero:
is a constant, the four acceleration is (pseudo-)orthogonal to the four velocity, i.e. the Minkowski inner product of the four-acceleration and the four-velocity is zero:
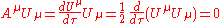
which is true for all world lines.
The geometric meaning of 4-acceleration is the curvature vector of the world line in Minkowski space.
for a massive particle is given by:
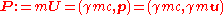
where m is the invariant mass
of the particle and p is the relativistic momentum.
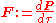
For a particle of constant mass, this is equivalent to

where
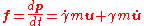 .
.
Theory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
, a four-vector is a vector in a four-dimensional real vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, called Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
. It differs from a vector in that it can be transformed by Lorentz transformations. The usage of the four-vector name tacitly assumes that its components refer to a standard basis. The components transform between these bases as the space
Space
Space is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...
and time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
coordinate differences,
 under spatial translations, rotations, and boosts (a change by a constant velocity to another inertial reference frame). The set of all such translations, rotations, and boosts (called Poincaré transformations) forms the Poincaré group
under spatial translations, rotations, and boosts (a change by a constant velocity to another inertial reference frame). The set of all such translations, rotations, and boosts (called Poincaré transformations) forms the Poincaré groupPoincaré group
In physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
. The set of rotations and boosts (Lorentz transformation
Lorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
s, described by 4×4 matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
) forms the Lorentz group
Lorentz group
In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...
.
This article considers four-vectors in the context of special relativity
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
. Although the concept of four-vectors also extends to general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, some of the results stated in this article require modification in general relativity.
Mathematics of four-vectors
A point in Minkowski spaceMinkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
is called an "event" and is described in a standard basis by a set of four coordinates such as

where
 = 0, 1, 2, 3, labels the spacetime
= 0, 1, 2, 3, labels the spacetimeSpacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s and where c is the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
. The definition
 ensures that all the coordinates have the same units (of distance). These coordinates are the components of the position four-vector for the event.
ensures that all the coordinates have the same units (of distance). These coordinates are the components of the position four-vector for the event.The displacement four-vector is defined to be an "arrow" linking two events:
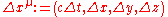
(Note that the position vector is the displacement vector when one of the two events is the origin of the coordinate system. Position vectors are relatively trivial; the general theory of four-vectors is concerned with displacement vectors.)
The scalar product of two four-vectors
 and
and  is defined (using Einstein notation
is defined (using Einstein notationEinstein notation
In mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention useful when dealing with coordinate formulae...
) as

where
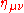 is the entry in the
is the entry in the  th row and
th row and  th column of the Minkowski metric
th column of the Minkowski metric  . Sometimes this inner product is called the Minkowski inner product. It is not a true inner product in the mathematical sense because it is not positive definite. (Note: some authors define
. Sometimes this inner product is called the Minkowski inner product. It is not a true inner product in the mathematical sense because it is not positive definite. (Note: some authors define  with the opposite sign:
with the opposite sign: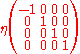
in which case
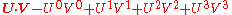
Either convention will work, since the primary significance of the Minkowski inner product is that for any two four-vectors, its value is invariant for all observers.)
An important property of the inner product is that it is invariant
Invariant (physics)
In mathematics and theoretical physics, an invariant is a property of a system which remains unchanged under some transformation.-Examples:In the current era, the immobility of polaris under the diurnal motion of the celestial sphere is a classical illustration of physical invariance.Another...
(that is, a scalar
Scalar (physics)
In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations , or by Lorentz transformations or space-time translations . This is in contrast to a vector...
): a change of coordinates does not result in a change in value of the inner product.
The inner product is often expressed as the effect of the dual vector of one vector on the other:

Here the
 s are the components of the dual vector
s are the components of the dual vector 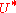 of
of  in the dual basis and called the covariant coordinates of
in the dual basis and called the covariant coordinates of  , while the original
, while the original 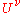 components are called the contravariant coordinates. Lower and upper indices indicate always covariant and contravariant coordinates, respectively.
components are called the contravariant coordinates. Lower and upper indices indicate always covariant and contravariant coordinates, respectively.The relation between the covariant and contravariant coordinates is:
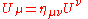 .
.The four-vectors are arrows on the spacetime diagram or Minkowski diagram
Minkowski diagram
The Minkowski diagram was developed in 1908 by Hermann Minkowski and provides an illustration of the properties of space and time in the special theory of relativity. It allows a quantitative understanding of the corresponding phenomena like time dilation and length contraction without mathematical...
. In this article, four-vectors will be referred to simply as vectors.
Four-vectors may be classified as either spacelike, timelike or null. Spacelike, timelike, and null vectors are ones whose inner product with themselves is less than, greater than, and equal to zero respectively (assuming Minkowski metric with signature
Metric signature
The signature of a metric tensor is the number of positive and negative eigenvalues of the metric. That is, the corresponding real symmetric matrix is diagonalised, and the diagonal entries of each sign counted...
(+,-,-,-)).
In special relativity (but not general relativity), the derivative of a four-vector with respect to a scalar (invariant) is itself a four-vector.
Examples of four-vectors in dynamics
When considering physical phenomena, differential equations arise naturally; however, when considering space and time derivatives of functions, it is unclear which reference frame these derivatives are taken with respect to. It is agreed that time derivatives are taken with respect to the proper timeProper time
In relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
(τ). As proper time is an invariant, this guarantees that the proper-time-derivative of any four-vector is itself a four-vector. It is then important to find a relation between this proper-time-derivative and another time derivative (using the time of an inertial reference frame). This relation is provided by the time transformation in the Lorentz transformations and is:
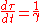
where γ is the Lorentz factor
Lorentz factor
The Lorentz factor or Lorentz term appears in several equations in special relativity, including time dilation, length contraction, and the relativistic mass formula. Because of its ubiquity, physicists generally represent it with the shorthand symbol γ . It gets its name from its earlier...
. Important four-vectors in relativity theory can now be defined.
Four-velocity
The four-velocityFour-velocity
In physics, in particular in special relativity and general relativity, the four-velocity of an object is a four-vector that replaces classicalvelocity...
of an
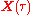 world line
world lineWorld line
In physics, the world line of an object is the unique path of that object as it travels through 4-dimensional spacetime. The concept of "world line" is distinguished from the concept of "orbit" or "trajectory" by the time dimension, and typically encompasses a large area of spacetime wherein...
is defined by:
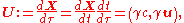
where, using suffix notation,
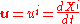
for . Notice that
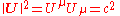
The geometric meaning of 4-velocity is the unit vector tangent to the world line in Minkowski space.
Four-acceleration
The four-accelerationFour-acceleration
In special relativity, four-acceleration is a four-vector and is defined as the change in four-velocity over the particle's proper time:whereandand \gamma_u is the Lorentz factor for the speed u...
is given by:
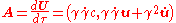
Since the magnitude
 of
of  is a constant, the four acceleration is (pseudo-)orthogonal to the four velocity, i.e. the Minkowski inner product of the four-acceleration and the four-velocity is zero:
is a constant, the four acceleration is (pseudo-)orthogonal to the four velocity, i.e. the Minkowski inner product of the four-acceleration and the four-velocity is zero: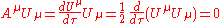
which is true for all world lines.
The geometric meaning of 4-acceleration is the curvature vector of the world line in Minkowski space.
Four-momentum
The four-momentumFour-momentum
In special relativity, four-momentum is the generalization of the classical three-dimensional momentum to four-dimensional spacetime. Momentum is a vector in three dimensions; similarly four-momentum is a four-vector in spacetime...
for a massive particle is given by:
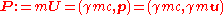
where m is the invariant mass
Invariant mass
The invariant mass, rest mass, intrinsic mass, proper mass or just mass is a characteristic of the total energy and momentum of an object or a system of objects that is the same in all frames of reference related by Lorentz transformations...
of the particle and p is the relativistic momentum.
Four-force
The four-force is defined by: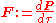
For a particle of constant mass, this is equivalent to

where
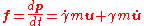 .
.Lorentz transformation
All four-vectors transform in the same manner. In the standard sets of inertial frames as shown by the graph,-
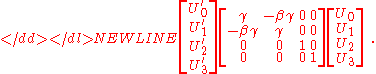
Physics of four-vectors
The power and elegance of the four-vector formalism may be demonstrated by seeing that known relations between energy and matter are embedded into it.
E = mc2
Here, an expression for the total energy of a particle will be derived. The kinetic energy (K) of a particle is defined analogously to the classical definition, namely as
with f as above. Noticing that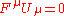 and expanding this out we get
and expanding this out we get
Hence
which yields
for some constant S. When the particle is at rest (u = 0), we take its kinetic energy to be zero (K = 0). This gives
Thus, we interpret the total energy E of the particle as composed of its kinetic energy K and its rest energy m c2. Thus, we have
E2 = p2c2 + m2c4
Using the relation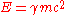 , we can write the four-momentum as
, we can write the four-momentum as
-
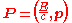 .
.
Taking the inner product of the four-momentum with itself in two different ways, we obtain the relation
i.e.
Hence
This last relation is useful in many areas of physics.
Examples of four-vectors in electromagnetism
Examples of four-vectors in electromagnetism include the four-currentFour-currentIn special and general relativity, the four-current is the Lorentz covariant four-vector that replaces the electromagnetic current density, or indeed any conventional charge current density...
defined by
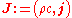
formed from the current density j and charge density ρ, and the electromagnetic four-potentialElectromagnetic four-potentialThe electromagnetic four-potential is a potential from which the electromagnetic field can be derived. It combines both the electric scalar potential and the magnetic vector potential into a single space-time four-vector. In a given reference frame, the first component is the scalar potential and...
defined by
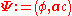
formed from the vector potential a and the scalar potential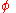 .
.
A plane electromagnetic wave can be described by the four-frequency defined as
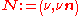
where is the frequency of the wave and n is a unit vector in the travel direction of the wave. Notice that
is the frequency of the wave and n is a unit vector in the travel direction of the wave. Notice that
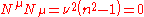
so that the four-frequency is always a null vector.
A wave packet of nearly monochromatic light can be characterized by the wave vectorWave vectorIn physics, a wave vector is a vector which helps describe a wave. Like any vector, it has a magnitude and direction, both of which are important: Its magnitude is either the wavenumber or angular wavenumber of the wave , and its direction is ordinarily the direction of wave propagation In...
, or four-wavevector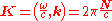
The 4-impulse of single photonPhotonIn physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
is
Four-vectors in quantum theory
In relativistic quantum mechanics, the probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
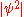 is substituted by the time component of a four-vector:
is substituted by the time component of a four-vector:
See also
- four-velocityFour-velocityIn physics, in particular in special relativity and general relativity, the four-velocity of an object is a four-vector that replaces classicalvelocity...
- four-accelerationFour-accelerationIn special relativity, four-acceleration is a four-vector and is defined as the change in four-velocity over the particle's proper time:whereandand \gamma_u is the Lorentz factor for the speed u...
- four-momentumFour-momentumIn special relativity, four-momentum is the generalization of the classical three-dimensional momentum to four-dimensional spacetime. Momentum is a vector in three dimensions; similarly four-momentum is a four-vector in spacetime...
- four-force
- four-currentFour-currentIn special and general relativity, the four-current is the Lorentz covariant four-vector that replaces the electromagnetic current density, or indeed any conventional charge current density...
- electromagnetic four-potentialElectromagnetic four-potentialThe electromagnetic four-potential is a potential from which the electromagnetic field can be derived. It combines both the electric scalar potential and the magnetic vector potential into a single space-time four-vector. In a given reference frame, the first component is the scalar potential and...
- four-gradientFour-gradientThe four-gradient is the four-vector generalization of the gradient:\partial_\alpha \ = \left...
- four-frequency
- paravectorParavectorThe name paravector is used for the sum of a scalar and a vector in any Clifford algebra This name was given by J. G...
- wave vectorWave vectorIn physics, a wave vector is a vector which helps describe a wave. Like any vector, it has a magnitude and direction, both of which are important: Its magnitude is either the wavenumber or angular wavenumber of the wave , and its direction is ordinarily the direction of wave propagation In...
- Dust (relativity)Dust (relativity)In special and general relativity, dust is the name conventionally given to a configuration of matter which can be interpreted as small bodies which interact only gravitationally....
Number-Flux 4-vector - Basic introduction to the mathematics of curved spacetimeBasic introduction to the mathematics of curved spacetimeThe mathematics of general relativity are very complex. In Newton's theories of motions, an object's mass and length remain constant as it changes speed, and the rate of passage of time also remains unchanged. As a result, many problems in Newtonian mechanics can be solved with algebra alone...
- Minkowski spaceMinkowski spaceIn physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
-