
Continuum mechanics
Encyclopedia
Continuum mechanics is a branch of mechanics
that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles. The French mathematician Augustin Louis Cauchy
was the first to formulate such models in the 19th century, but research in the area continues today.
Modelling an object as a continuum assumes that the substance of the object completely fills the space it occupies. Modelling objects in this way ignores the fact that matter is made of atom
s, and so is not continuous; however, on length scale
s much greater than that of inter-atomic distances, such models are highly accurate. Fundamental physical laws such as the conservation of mass
, the conservation of momentum, and the conservation of energy
may be applied to such models to derive differential equations describing the behavior of such objects, and some information about the particular material studied is added through a constitutive relation.
Continuum mechanics deals with physical properties of solids and fluids which are independent of any particular coordinate system
in which they are observed. These physical properties are then represented by tensor
s, which are mathematical objects that have the required property of being independent of coordinate system. These tensors can be expressed in coordinate systems for computational convenience.
elements with properties being those of the bulk material.
The validity of the continuum assumption may be verified by a theoretical analysis, in which either some clear periodicity is identified or statistical homogeneity
and ergodicity
of the microstructure
exists. More specifically, the continuum hypothesis/assumption hinges on the concepts of a representative volume element (RVE)
(sometimes called "representative elementary volume") and separation of scales based on the Hill–Mandel condition. This condition provides a link between an experimentalist's and a theoretician's viewpoint on constitutive equations (linear and nonlinear elastic/inelastic or coupled fields) as well as a way of spatial and statistical averaging of the microstructure.
When the separation of scales does not hold, or when one wants to establish a continuum of a finer resolution than that of the RVE size, one employs a statistical volume element (SVE), which, in turn, leads to random continuum fields. The latter then provide a micromechanics basis for stochastic finite elements (SFE). The levels of SVE and RVE link continuum mechanics to statistical mechanics
. The RVE may be assessed only in a limited way via experimental testing: when the constitutive response becomes spatially homogeneous.
Specifically for fluid
s, the Knudsen number
is used to assess to what extent the approximation of continuity can be made.
to the material body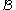 being modeled. The points within this region are called particles or material points. Different configurations or states of the body correspond to different regions in Euclidean space. The region corresponding to the body's configuration at time
being modeled. The points within this region are called particles or material points. Different configurations or states of the body correspond to different regions in Euclidean space. The region corresponding to the body's configuration at time 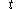 is labeled
is labeled 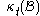 .
.
A particular particle within the body in a particular configuration is characterized by a position vector
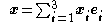 ,
,
where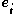 are the coordinate vector
are the coordinate vector
s in some frame of reference
chosen for the problem (See figure 1). This vector can be expressed as a function
of the particle position in some reference configuration, for example the configuration at the initial time, so that
in some reference configuration, for example the configuration at the initial time, so that
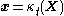 .
.
This function needs to have various properties so that the model makes physical sense.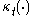 needs to be:
needs to be:
For the mathematical formulation of the model,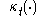 is also assumed to be twice continuously differentiable, so that differential equations describing the motion may be formulated.
is also assumed to be twice continuously differentiable, so that differential equations describing the motion may be formulated.
Following the classical dynamics of Newton
and Euler
, the motion of a material body is produced by the action of externally applied forces which are assumed to be of two kinds: surface forces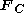 and body forces
and body forces 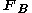 . Thus, the total force
. Thus, the total force  applied to a body or to a portion of the body can be expressed as:
applied to a body or to a portion of the body can be expressed as:

Surface forces or contact forces, expressed as force per unit area, can act either on the bounding surface of the body, as a result of mechanical contact with other bodies, or on imaginary internal surfaces that bound portions of the body, as a result of the mechanical interaction between the parts of the body to either side of the surface (Euler-Cauchy's stress principle). When a body is acted upon by external contact forces, internal contact forces are then transmitted from point to point inside the body to balance their action, according to Newton's second law of motion
of conservation of linear momentum and angular momentum
(for continuous bodies these laws are called the Euler's equations of motion
). The internal contact forces are related to the body's deformation
through constitutive equations. The internal contact forces may be mathematically described by how they relate to the motion of the body, independent of the body's material makeup.
The distribution of internal contact forces throughout the volume of the body is assumed to be continuous. Therefore, there exists a contact force density or Cauchy traction field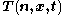 that represents this distribution in a particular configuration of the body at a given time
that represents this distribution in a particular configuration of the body at a given time  . It is not a vector field because it depends not only on the position
. It is not a vector field because it depends not only on the position 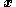 of a particular material point, but also on the local orientation of the surface element as defined by its normal vector
of a particular material point, but also on the local orientation of the surface element as defined by its normal vector  .
.
Any differential area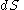 with normal vector
with normal vector  of a given internal surface area
of a given internal surface area 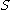 , bounding a portion of the body, experiences a contact force
, bounding a portion of the body, experiences a contact force 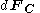 arising from the contact between both portions of the body on each side of
arising from the contact between both portions of the body on each side of 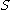 , and it is given by
, and it is given by
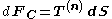
where is the surface traction, also called stress vector, traction, or traction vector,. The stress vector is a frame-indifferent vector (see Euler-Cauchy's stress principle).
is the surface traction, also called stress vector, traction, or traction vector,. The stress vector is a frame-indifferent vector (see Euler-Cauchy's stress principle).
The total contact force on the particular internal surface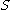 is then expressed as the sum (surface integral
is then expressed as the sum (surface integral
) of the contact forces on all differential surfaces :
:
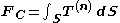
In continuum mechanics a body is considered stress-free if the only forces present are those inter-atomic forces (ionic
, metallic
, and van der Waals force
s) required to hold the body together and to keep its shape in the absence of all external influences, including gravitational attraction. Stresses generated during manufacture of the body to a specific configuration are also excluded when considering stresses in a body. Therefore, the stresses considered in continuum mechanics are only those produced by deformation of the body, sc. only relative changes in stress are considered, not the absolute values of stress.
Body forces are forces originating from sources outside of the body that act on the volume (or mass) of the body. Saying that body forces are due to outside sources implies that the interaction between different parts of the body (internal forces) are manifested through the contact forces alone. These forces arise from the presence of the body in force fields, e.g. gravitational field
(gravitational forces) or electromagnetic field (electromagnetic forces), or from inertial forces
when bodies are in motion. As the mass of a continuous body is assumed to be continuously distributed, any force originating from the mass is also continuously distributed. Thus, body forces are specified by vector fields which are assumed to be continuous over the entire volume of the body, i.e. acting on every point in it. Body forces are represented by a body force density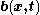 (per unit of mass), which is a frame-indifferent vector field.
(per unit of mass), which is a frame-indifferent vector field.
In the case of gravitational forces, the intensity of the force depends on, or is proportional to, the mass density of the material, and it is specified in terms of force per unit mass (
of the material, and it is specified in terms of force per unit mass (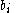 ) or per unit volume (
) or per unit volume ( ). These two specifications are related through the material density by the equation
). These two specifications are related through the material density by the equation 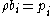 . Similarly, the intensity of electromagnetic forces depends upon the strength (electric charge
. Similarly, the intensity of electromagnetic forces depends upon the strength (electric charge
) of the electromagnetic field.
The total body force applied to a continuous body is expressed as
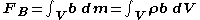
Body forces and contact forces acting on the body lead to corresponding moments of force (torque
s) relative to a given point. Thus, the total applied torque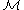 about the origin is given by
about the origin is given by
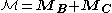
In certain situations, not commonly considered in the analysis of the mechanical behavior or materials, it becomes necessary to include two other types of forces: these are body moments and couple stresses (surface couples, contact torques). Body moments, or body couples, are moments per unit volume or per unit mass applied to the volume of the body. Couple stresses are moments per unit area applied on a surface. Both are important in the analysis of stress for a polarized dielectric solid under the action of an electric field, materials where the molecular structure is taken into consideration (e.g. bones), solids under the action of an external magnetic field, and the dislocation theory of metals.
Materials that exhibit body couples and couple stresses in addition to moments produced exclusively by forces are called polar materials. Non-polar materials are then those materials with only moments of forces. In the classical branches of continuum mechanics the development of the theory of stresses is based on non-polar materials.
Thus, the sum of all applied forces and torques (with respect to the origin of the coordinate system) in the body can be given by
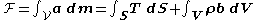
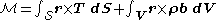
. The displacement of a body has two components: a rigid-body displacement and a deformation
. A rigid-body displacement consists of a simultaneous translation and rotation of the body without changing its shape or size. Deformation implies the change in shape and/or size of the body from an initial or undeformed configuration to a current or deformed configuration
to a current or deformed configuration  (Figure 2).
(Figure 2).
The motion of a continuum body is a continuous time sequence of displacements. Thus, the material body will occupy different configurations at different times so that a particle occupies a series of points in space which describe a pathline.
There is continuity during deformation or motion of a continuum body in the sense that:
It is convenient to identify a reference configuration or initial condition which all subsequent configurations are referenced from. The reference configuration need not be one that the body will ever occupy. Often, the configuration at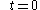 is considered the reference configuration,
is considered the reference configuration, 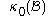 . The components
. The components  of the position vector
of the position vector 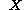 of a particle, taken with respect to the reference configuration, are called the material or reference coordinates.
of a particle, taken with respect to the reference configuration, are called the material or reference coordinates.
When analyzing the deformation
or motion of solids, or the flow
of fluids, it is necessary to describe the sequence or evolution of configurations throughout time. One description for motion is made in terms of the material or referential coordinates, called material description or Lagrangian description.
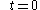 . An observer standing in the referential frame of reference observes the changes in the position and physical properties as the material body moves in space as time progresses. The results obtained are independent of the choice of initial time and reference configuration,
. An observer standing in the referential frame of reference observes the changes in the position and physical properties as the material body moves in space as time progresses. The results obtained are independent of the choice of initial time and reference configuration, 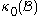 . This description is normally used in solid mechanics
. This description is normally used in solid mechanics
.
In the Lagrangian description, the motion of a continuum body is expressed by the mapping function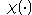 (Figure 2),
(Figure 2),
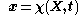
which is a mapping of the initial configuration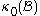 onto the current configuration
onto the current configuration 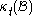 , giving a geometrical correspondence between them, i.e. giving the position vector
, giving a geometrical correspondence between them, i.e. giving the position vector 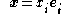 that a particle
that a particle 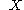 , with a position vector
, with a position vector 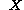 in the undeformed or reference configuration
in the undeformed or reference configuration 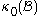 , will occupy in the current or deformed configuration
, will occupy in the current or deformed configuration 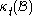 at time
at time  . The components
. The components 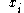 are called the spatial coordinates.
are called the spatial coordinates.
Physical and kinematic properties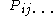 , i.e. thermodynamic properties and velocity, which describe or characterize features of the material body, are expressed as continuous functions of position and time, i.e.
, i.e. thermodynamic properties and velocity, which describe or characterize features of the material body, are expressed as continuous functions of position and time, i.e. 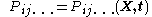 .
.
The material derivative of any property of a continuum, which may be a scalar, vector, or tensor, is the time rate of change of that property for a specific group of particles of the moving continuum body. The material derivative is also known as the substantial derivative, or comoving derivative, or convective derivative. It can be thought as the rate at which the property changes when measured by an observer traveling with that group of particles.
of a continuum, which may be a scalar, vector, or tensor, is the time rate of change of that property for a specific group of particles of the moving continuum body. The material derivative is also known as the substantial derivative, or comoving derivative, or convective derivative. It can be thought as the rate at which the property changes when measured by an observer traveling with that group of particles.
In the Lagrangian description, the material derivative of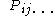 is simply the partial derivative with respect to time, and the position vector
is simply the partial derivative with respect to time, and the position vector 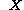 is held constant as it does not change with time. Thus, we have
is held constant as it does not change with time. Thus, we have
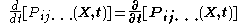
The instantaneous position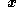 is a property of a particle, and its material derivative is the instantaneous velocity
is a property of a particle, and its material derivative is the instantaneous velocity  of the particle. Therefore, the velocity field of the continuum is given by
of the particle. Therefore, the velocity field of the continuum is given by
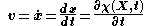
Similarly, the acceleration field is given by
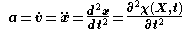
Continuity in the Lagrangian description is expressed by the spatial and temporal continuity of the mapping from the reference configuration to the current configuration of the material points. All physical quantities characterizing the continuum are described this way. In this sense, the function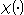 and
and 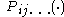 are single-valued and continuous, with continuous derivatives with respect to space and time to whatever order is required, usually to the second or third.
are single-valued and continuous, with continuous derivatives with respect to space and time to whatever order is required, usually to the second or third.
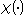 to trace backwards where the particle currently located at
to trace backwards where the particle currently located at 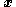 was located in the initial or referenced configuration
was located in the initial or referenced configuration 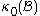 . In this case the description of motion is made in terms of the spatial coordinates, in which case is called the spatial description or Eulerian description, i.e. the current configuration is taken as the reference configuration.
. In this case the description of motion is made in terms of the spatial coordinates, in which case is called the spatial description or Eulerian description, i.e. the current configuration is taken as the reference configuration.
The Eulerian description, introduced by d'Alembert, focuses on the current configuration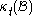 , giving attention to what is occurring at a fixed point in space as time progresses, instead of giving attention to individual particles as they move through space and time. This approach is conveniently applied in the study of fluid flow
, giving attention to what is occurring at a fixed point in space as time progresses, instead of giving attention to individual particles as they move through space and time. This approach is conveniently applied in the study of fluid flow
where the kinematic property of greatest interest is the rate at which change is taking place rather than the shape of the body of fluid at a reference time.
Mathematically, the motion of a continuum using the Eulerian description is expressed by the mapping function
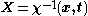
which provides a tracing of the particle which now occupies the position in the current configuration
in the current configuration 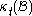 to its original position
to its original position  in the initial configuration
in the initial configuration 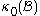 .
.
A necessary and sufficient condition for this inverse function to exist is that the determinant of the Jacobian Matrix, often referred to simply as the Jacobian, should be different from zero. Thus,
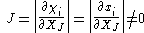
In the Eulerian description, the physical properties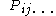 are expressed as
are expressed as
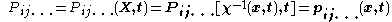
where the functional form of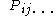 in the Lagrangian description is not the same as the form of
in the Lagrangian description is not the same as the form of 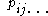 in the Eulerian description.
in the Eulerian description.
The material derivative of , using the chain rule, is then
, using the chain rule, is then
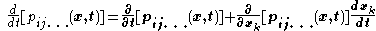
The first term on the right-hand side of this equation gives the local rate of change of the property occurring at position
occurring at position 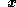 . The second term of the right-hand side is the convective rate of change and expresses the contribution of the particle changing position in space (motion).
. The second term of the right-hand side is the convective rate of change and expresses the contribution of the particle changing position in space (motion).
Continuity in the Eulerian description is expressed by the spatial and temporal continuity and continuous differentiability of the velocity field. All physical quantities are defined this way at each instant of time, in the current configuration, as a function of the vector position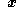 .
.
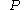 in the undeformed configuration and deformed configuration is called the displacement vector
in the undeformed configuration and deformed configuration is called the displacement vector
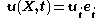 , in the Lagrangian description, or
, in the Lagrangian description, or  , in the Eulerian description.
, in the Eulerian description.
A displacement field is a vector field of all displacement vectors for all particles in the body, which relates the deformed configuration with the undeformed configuration. It is convenient to do the analysis of deformation or motion of a continuum body in terms of the displacement field, In general, the displacement field is expressed in terms of the material coordinates as
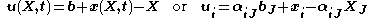
or in terms of the spatial coordinates as

where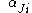 are the direction cosines between the material and spatial coordinate systems with unit vectors
are the direction cosines between the material and spatial coordinate systems with unit vectors 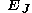 and
and 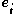 , respectively. Thus
, respectively. Thus
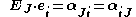
and the relationship between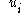 and
and 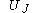 is then given by
is then given by
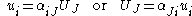
Knowing that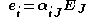
then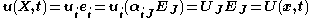
It is common to superimpose the coordinate systems for the undeformed and deformed configurations, which results in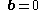 , and the direction cosines become Kronecker deltas, i.e.
, and the direction cosines become Kronecker deltas, i.e.
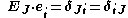
Thus, we have
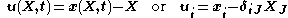
or in terms of the spatial coordinates as
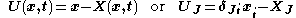
, momentum, and energy
. Kinematic relations and constitutive equations are needed to complete the system of governing equations. Physical restrictions on the form of the constitutive relations can be applied by requiring that the second law of thermodynamics
be satisfied under all conditions. In the continuum mechanics of solids, the second law of thermodynamics is satisfied if the Clausius–Duhem form of the entropy inequality is satisfied.
The balance laws express the idea that the rate of change of a quantity (mass, momentum, energy) in a volume must arise from three causes:
Let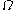 be the body (an open subset of Euclidean space) and let
be the body (an open subset of Euclidean space) and let 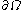 be its surface (the boundary of
be its surface (the boundary of 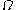 ).
).
Let the motion of material points in the body be described by the map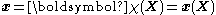
where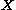 is the position of a point in the initial configuration and
is the position of a point in the initial configuration and 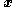 is the location of the same point in the deformed configuration.
is the location of the same point in the deformed configuration.
The deformation gradient is given by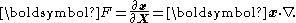
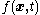 be a physical quantity that is flowing through the body. Let
be a physical quantity that is flowing through the body. Let 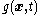 be sources on the surface of the body and let
be sources on the surface of the body and let 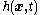 be sources inside the body. Let
be sources inside the body. Let  be the outward unit normal to the surface
be the outward unit normal to the surface  . Let
. Let 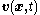 be the velocity of the physical particles that carry the physical quantity that is flowing. Also, let the speed at which the bounding surface
be the velocity of the physical particles that carry the physical quantity that is flowing. Also, let the speed at which the bounding surface  is moving be
is moving be 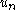 (in the direction
(in the direction  ).
).
Then, balance laws can be expressed in the general form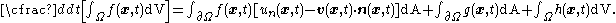
Note that the functions ,
, 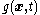 , and
, and 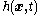 can be scalar valued, vector valued, or tensor valued - depending on the physical quantity that the balance equation deals with. If there are internal boundaries in the body, jump discontinuities also need to be specified in the balance laws.
can be scalar valued, vector valued, or tensor valued - depending on the physical quantity that the balance equation deals with. If there are internal boundaries in the body, jump discontinuities also need to be specified in the balance laws.
If we take the Lagrangian
point of view, it can be shown that the balance laws of mass, momentum, and energy for a solid can be written as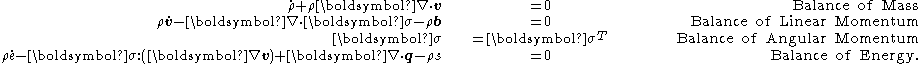
In the above equations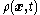 is the mass density (current),
is the mass density (current), 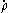 is the material time derivative of
is the material time derivative of 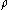 ,
, 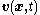 is the particle velocity,
is the particle velocity, 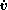 is the material time derivative of
is the material time derivative of  ,
, 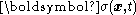 is the Cauchy stress tensor,
is the Cauchy stress tensor, 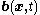 is the body force density,
is the body force density, 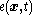 is the internal energy per unit mass,
is the internal energy per unit mass, 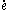 is the material time derivative of
is the material time derivative of  ,
, 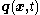 is the heat flux vector, and
is the heat flux vector, and  is an energy source per unit mass.
is an energy source per unit mass.
With respect to the reference configuration, the balance laws can be written as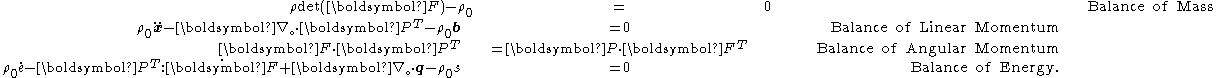
In the above,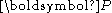 is the first Piola-Kirchhoff stress tensor, and
is the first Piola-Kirchhoff stress tensor, and 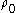 is the mass density in the reference configuration. The first Piola-Kirchhoff stress tensor is related to the Cauchy stress tensor by
is the mass density in the reference configuration. The first Piola-Kirchhoff stress tensor is related to the Cauchy stress tensor by
We can alternatively define the nominal stress tensor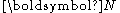 which is the transpose of the first Piola-Kirchhoff stress tensor such that
which is the transpose of the first Piola-Kirchhoff stress tensor such that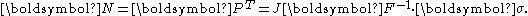
Then the balance laws become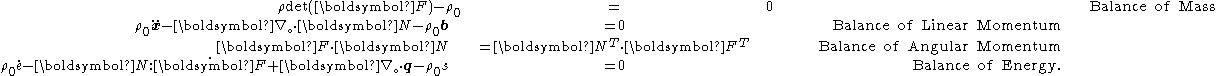
The operators in the above equations are defined as such that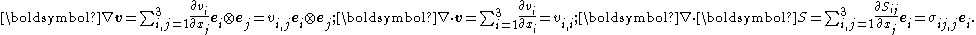
where is a vector field,
is a vector field, 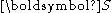 is a second-order tensor field, and
is a second-order tensor field, and 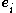 are the components of an orthonormal basis in the current configuration. Also,
are the components of an orthonormal basis in the current configuration. Also,
where is a vector field,
is a vector field,  is a second-order tensor field, and
is a second-order tensor field, and 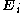 are the components of an orthonormal basis in the reference configuration.
are the components of an orthonormal basis in the reference configuration.
The inner product is defined as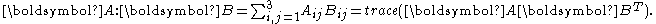
Just like in the balance laws in the previous section, we assume that there is a flux of a quantity, a source of the quantity, and an internal density of the quantity per unit mass. The quantity of interest in this case is the entropy. Thus, we assume that there is an entropy flux, an entropy source, and an internal entropy density per unit mass (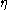 ) in the region of interest.
) in the region of interest.
Let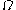 be such a region and let
be such a region and let  be its boundary. Then the second law of thermodynamics states that the rate of increase of
be its boundary. Then the second law of thermodynamics states that the rate of increase of 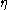 in this region is greater than or equal to the sum of that supplied to
in this region is greater than or equal to the sum of that supplied to 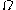 (as a flux or from internal sources) and the change of the internal entropy density due to material flowing in and out of the region.
(as a flux or from internal sources) and the change of the internal entropy density due to material flowing in and out of the region.
Let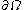 move with a velocity
move with a velocity 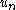 and let particles inside
and let particles inside 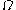 have velocities
have velocities  . Let
. Let  be the unit outward normal to the surface
be the unit outward normal to the surface 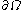 . Let
. Let 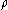 be the density of matter in the region,
be the density of matter in the region, 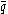 be the entropy flux at the surface, and
be the entropy flux at the surface, and  be the entropy source per unit mass.
be the entropy source per unit mass.
Then the entropy inequality may be written as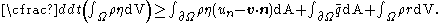
The scalar entropy flux can be related to the vector flux at the surface by the relation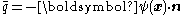 . Under the assumption of incrementally isothermal conditions, we have
. Under the assumption of incrementally isothermal conditions, we have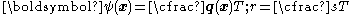
where is the heat flux vector,
is the heat flux vector,  is a energy source per unit mass, and
is a energy source per unit mass, and  is the absolute temperature of a material point at
is the absolute temperature of a material point at  at time
at time  .
.
We then have the Clausius–Duhem inequality in integral form:
We can show that the entropy inequality may be written in differential form as
In terms of the Cauchy stress and the internal energy, the Clausius–Duhem inequality may be written as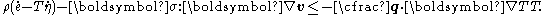
Mechanics
Mechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles. The French mathematician Augustin Louis Cauchy
Augustin Louis Cauchy
Baron Augustin-Louis Cauchy was a French mathematician who was an early pioneer of analysis. He started the project of formulating and proving the theorems of infinitesimal calculus in a rigorous manner, rejecting the heuristic principle of the generality of algebra exploited by earlier authors...
was the first to formulate such models in the 19th century, but research in the area continues today.
Modelling an object as a continuum assumes that the substance of the object completely fills the space it occupies. Modelling objects in this way ignores the fact that matter is made of atom
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
s, and so is not continuous; however, on length scale
Length scale
In physics, length scale is a particular length or distance determined with the precision of one order of magnitude. The concept of length scale is particularly important because physical phenomena of different length scales cannot affect each other and are said to decouple...
s much greater than that of inter-atomic distances, such models are highly accurate. Fundamental physical laws such as the conservation of mass
Conservation of mass
The law of conservation of mass, also known as the principle of mass/matter conservation, states that the mass of an isolated system will remain constant over time...
, the conservation of momentum, and the conservation of energy
Conservation of energy
The nineteenth century law of conservation of energy is a law of physics. It states that the total amount of energy in an isolated system remains constant over time. The total energy is said to be conserved over time...
may be applied to such models to derive differential equations describing the behavior of such objects, and some information about the particular material studied is added through a constitutive relation.
Continuum mechanics deals with physical properties of solids and fluids which are independent of any particular coordinate system
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
in which they are observed. These physical properties are then represented by tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
s, which are mathematical objects that have the required property of being independent of coordinate system. These tensors can be expressed in coordinate systems for computational convenience.
The concept of a continuum
Materials, such as solids, liquids and gases, are composed of molecules separated by empty space. On a macroscopic scale, materials have cracks and discontinuities. However, certain physical phenomena can be modelled assuming the materials exist as a continuum, meaning the matter in the body is continuously distributed and fills the entire region of space it occupies. A continuum is a body that can be continually sub-divided into infinitesimalInfinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
elements with properties being those of the bulk material.
The validity of the continuum assumption may be verified by a theoretical analysis, in which either some clear periodicity is identified or statistical homogeneity
Homogeneity (statistics)
In statistics, homogeneity and its opposite, heterogeneity, arise in describing the properties of a dataset, or several datasets. They relate to the validity of the often convenient assumption that the statistical properties of any one part of an overall dataset are the same as any other part...
and ergodicity
Ergodicity
In mathematics, the term ergodic is used to describe a dynamical system which, broadly speaking, has the same behavior averaged over time as averaged over space. In physics the term is used to imply that a system satisfies the ergodic hypothesis of thermodynamics.-Etymology:The word ergodic is...
of the microstructure
Microstructure
Microstructure is defined as the structure of a prepared surface or thin foil of material as revealed by a microscope above 25× magnification...
exists. More specifically, the continuum hypothesis/assumption hinges on the concepts of a representative volume element (RVE)
Representative elementary volume
In hydrogeology, the representative elementary volume is the smallest volume over which a measurement can be made that will yield a value representative of the whole. Below REV, the parameter is not defined and the material can not be treated as a continuum.In order to establish a given porous...
(sometimes called "representative elementary volume") and separation of scales based on the Hill–Mandel condition. This condition provides a link between an experimentalist's and a theoretician's viewpoint on constitutive equations (linear and nonlinear elastic/inelastic or coupled fields) as well as a way of spatial and statistical averaging of the microstructure.
When the separation of scales does not hold, or when one wants to establish a continuum of a finer resolution than that of the RVE size, one employs a statistical volume element (SVE), which, in turn, leads to random continuum fields. The latter then provide a micromechanics basis for stochastic finite elements (SFE). The levels of SVE and RVE link continuum mechanics to statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
. The RVE may be assessed only in a limited way via experimental testing: when the constitutive response becomes spatially homogeneous.
Specifically for fluid
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
s, the Knudsen number
Knudsen number
The Knudsen number is a dimensionless number defined as the ratio of the molecular mean free path length to a representative physical length scale. This length scale could be, for example, the radius of a body in a fluid...
is used to assess to what extent the approximation of continuity can be made.
Formulation of models
Continuum mechanics models begin by assigning a region in three dimensional Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
to the material body
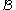 being modeled. The points within this region are called particles or material points. Different configurations or states of the body correspond to different regions in Euclidean space. The region corresponding to the body's configuration at time
being modeled. The points within this region are called particles or material points. Different configurations or states of the body correspond to different regions in Euclidean space. The region corresponding to the body's configuration at time 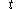 is labeled
is labeled 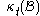 .
.A particular particle within the body in a particular configuration is characterized by a position vector
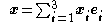 ,
,where
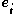 are the coordinate vector
are the coordinate vectorCoordinate vector
In linear algebra, a coordinate vector is an explicit representation of a vector in an abstract vector space as an ordered list of numbers or, equivalently, as an element of the coordinate space Fn....
s in some frame of reference
Frame of reference
A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...
chosen for the problem (See figure 1). This vector can be expressed as a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of the particle position
 in some reference configuration, for example the configuration at the initial time, so that
in some reference configuration, for example the configuration at the initial time, so that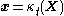 .
.This function needs to have various properties so that the model makes physical sense.
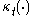 needs to be:
needs to be:
- continuous in time, so that the body changes in a way which is realistic,
- globally invertibleInverse functionIn mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
at all times, so that the body cannot intersect itself, - orientation-preserving, as transformations which produce mirror reflections are not possible in nature.
For the mathematical formulation of the model,
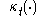 is also assumed to be twice continuously differentiable, so that differential equations describing the motion may be formulated.
is also assumed to be twice continuously differentiable, so that differential equations describing the motion may be formulated.Forces in a continuum
Continuum mechanics deals with deformable bodies, as opposed to rigid bodies. A solid is a deformable body that possesses shear strength, sc. a solid can support shear forces (forces parallel to the material surface on which they act). Fluids, on the other hand, do not sustain shear forces. For the study of the mechanical behavior of solids and fluids these are assumed to be continuous bodies, which means that the matter fills the entire region of space it occupies, despite the fact that matter is made of atoms, has voids, and is discrete. Therefore, when continuum mechanics refers to a point or particle in a continuous body it does not describe a point in the interatomic space or an atomic particle, rather an idealized part of the body occupying that point.Following the classical dynamics of Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
and Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
, the motion of a material body is produced by the action of externally applied forces which are assumed to be of two kinds: surface forces
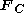 and body forces
and body forces 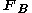 . Thus, the total force
. Thus, the total force  applied to a body or to a portion of the body can be expressed as:
applied to a body or to a portion of the body can be expressed as:
Surface forces or contact forces, expressed as force per unit area, can act either on the bounding surface of the body, as a result of mechanical contact with other bodies, or on imaginary internal surfaces that bound portions of the body, as a result of the mechanical interaction between the parts of the body to either side of the surface (Euler-Cauchy's stress principle). When a body is acted upon by external contact forces, internal contact forces are then transmitted from point to point inside the body to balance their action, according to Newton's second law of motion
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
of conservation of linear momentum and angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
(for continuous bodies these laws are called the Euler's equations of motion
Euler's laws
Euler's laws of motion, formulated by Leonhard Euler about 50 years after Isaac Newton formulated his laws about the motion of particles, extends them to rigid body motion.-Euler's first law:...
). The internal contact forces are related to the body's deformation
Deformation (mechanics)
Deformation in continuum mechanics is the transformation of a body from a reference configuration to a current configuration. A configuration is a set containing the positions of all particles of the body...
through constitutive equations. The internal contact forces may be mathematically described by how they relate to the motion of the body, independent of the body's material makeup.
The distribution of internal contact forces throughout the volume of the body is assumed to be continuous. Therefore, there exists a contact force density or Cauchy traction field
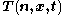 that represents this distribution in a particular configuration of the body at a given time
that represents this distribution in a particular configuration of the body at a given time  . It is not a vector field because it depends not only on the position
. It is not a vector field because it depends not only on the position 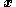 of a particular material point, but also on the local orientation of the surface element as defined by its normal vector
of a particular material point, but also on the local orientation of the surface element as defined by its normal vector  .
.Any differential area
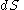 with normal vector
with normal vector  of a given internal surface area
of a given internal surface area 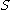 , bounding a portion of the body, experiences a contact force
, bounding a portion of the body, experiences a contact force 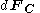 arising from the contact between both portions of the body on each side of
arising from the contact between both portions of the body on each side of 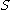 , and it is given by
, and it is given by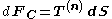
where
 is the surface traction, also called stress vector, traction, or traction vector,. The stress vector is a frame-indifferent vector (see Euler-Cauchy's stress principle).
is the surface traction, also called stress vector, traction, or traction vector,. The stress vector is a frame-indifferent vector (see Euler-Cauchy's stress principle).The total contact force on the particular internal surface
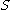 is then expressed as the sum (surface integral
is then expressed as the sum (surface integralSurface integral
In mathematics, a surface integral is a definite integral taken over a surface ; it can be thought of as the double integral analog of the line integral...
) of the contact forces on all differential surfaces
 :
: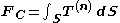
In continuum mechanics a body is considered stress-free if the only forces present are those inter-atomic forces (ionic
Ionic bond
An ionic bond is a type of chemical bond formed through an electrostatic attraction between two oppositely charged ions. Ionic bonds are formed between a cation, which is usually a metal, and an anion, which is usually a nonmetal. Pure ionic bonding cannot exist: all ionic compounds have some...
, metallic
Metallic bond
Metallic bonding is the electrostatic attractive forces between the delocalized electrons, called conduction electrons, gathered in an "electron sea", and the positively charged metal ions...
, and van der Waals force
Van der Waals force
In physical chemistry, the van der Waals force , named after Dutch scientist Johannes Diderik van der Waals, is the sum of the attractive or repulsive forces between molecules other than those due to covalent bonds or to the electrostatic interaction of ions with one another or with neutral...
s) required to hold the body together and to keep its shape in the absence of all external influences, including gravitational attraction. Stresses generated during manufacture of the body to a specific configuration are also excluded when considering stresses in a body. Therefore, the stresses considered in continuum mechanics are only those produced by deformation of the body, sc. only relative changes in stress are considered, not the absolute values of stress.
Body forces are forces originating from sources outside of the body that act on the volume (or mass) of the body. Saying that body forces are due to outside sources implies that the interaction between different parts of the body (internal forces) are manifested through the contact forces alone. These forces arise from the presence of the body in force fields, e.g. gravitational field
Gravitational field
The gravitational field is a model used in physics to explain the existence of gravity. In its original concept, gravity was a force between point masses...
(gravitational forces) or electromagnetic field (electromagnetic forces), or from inertial forces
Fictitious force
A fictitious force, also called a pseudo force, d'Alembert force or inertial force, is an apparent force that acts on all masses in a non-inertial frame of reference, such as a rotating reference frame....
when bodies are in motion. As the mass of a continuous body is assumed to be continuously distributed, any force originating from the mass is also continuously distributed. Thus, body forces are specified by vector fields which are assumed to be continuous over the entire volume of the body, i.e. acting on every point in it. Body forces are represented by a body force density
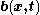 (per unit of mass), which is a frame-indifferent vector field.
(per unit of mass), which is a frame-indifferent vector field.In the case of gravitational forces, the intensity of the force depends on, or is proportional to, the mass density
 of the material, and it is specified in terms of force per unit mass (
of the material, and it is specified in terms of force per unit mass (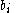 ) or per unit volume (
) or per unit volume ( ). These two specifications are related through the material density by the equation
). These two specifications are related through the material density by the equation 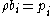 . Similarly, the intensity of electromagnetic forces depends upon the strength (electric charge
. Similarly, the intensity of electromagnetic forces depends upon the strength (electric chargeElectric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
) of the electromagnetic field.
The total body force applied to a continuous body is expressed as
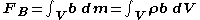
Body forces and contact forces acting on the body lead to corresponding moments of force (torque
Torque
Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....
s) relative to a given point. Thus, the total applied torque
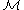 about the origin is given by
about the origin is given by
In certain situations, not commonly considered in the analysis of the mechanical behavior or materials, it becomes necessary to include two other types of forces: these are body moments and couple stresses (surface couples, contact torques). Body moments, or body couples, are moments per unit volume or per unit mass applied to the volume of the body. Couple stresses are moments per unit area applied on a surface. Both are important in the analysis of stress for a polarized dielectric solid under the action of an electric field, materials where the molecular structure is taken into consideration (e.g. bones), solids under the action of an external magnetic field, and the dislocation theory of metals.
Materials that exhibit body couples and couple stresses in addition to moments produced exclusively by forces are called polar materials. Non-polar materials are then those materials with only moments of forces. In the classical branches of continuum mechanics the development of the theory of stresses is based on non-polar materials.
Thus, the sum of all applied forces and torques (with respect to the origin of the coordinate system) in the body can be given by
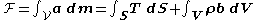
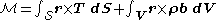
Kinematics: deformation and motion
A change in the configuration of a continuum body results in a displacementDisplacement field (mechanics)
A displacement field is an assignment of displacement vectors for all points in a region or body that is displaced from one state to another. A displacement vector specifies the position of a point or a particle in reference to an origin or to a previous position...
. The displacement of a body has two components: a rigid-body displacement and a deformation
Deformation (mechanics)
Deformation in continuum mechanics is the transformation of a body from a reference configuration to a current configuration. A configuration is a set containing the positions of all particles of the body...
. A rigid-body displacement consists of a simultaneous translation and rotation of the body without changing its shape or size. Deformation implies the change in shape and/or size of the body from an initial or undeformed configuration
 to a current or deformed configuration
to a current or deformed configuration  (Figure 2).
(Figure 2).The motion of a continuum body is a continuous time sequence of displacements. Thus, the material body will occupy different configurations at different times so that a particle occupies a series of points in space which describe a pathline.
There is continuity during deformation or motion of a continuum body in the sense that:
- The material points forming a closed curve at any instant will always form a closed curve at any subsequent time.
- The material points forming a closed surface at any instant will always form a closed surface at any subsequent time and the matter within the closed surface will always remain within.
It is convenient to identify a reference configuration or initial condition which all subsequent configurations are referenced from. The reference configuration need not be one that the body will ever occupy. Often, the configuration at
 is considered the reference configuration,
is considered the reference configuration, 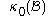 . The components
. The components  of the position vector
of the position vector 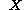 of a particle, taken with respect to the reference configuration, are called the material or reference coordinates.
of a particle, taken with respect to the reference configuration, are called the material or reference coordinates.When analyzing the deformation
Deformation (mechanics)
Deformation in continuum mechanics is the transformation of a body from a reference configuration to a current configuration. A configuration is a set containing the positions of all particles of the body...
or motion of solids, or the flow
Fluid mechanics
Fluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...
of fluids, it is necessary to describe the sequence or evolution of configurations throughout time. One description for motion is made in terms of the material or referential coordinates, called material description or Lagrangian description.
Lagrangian description
In the Lagrangian description the position and physical properties of the particles are described in terms of the material or referential coordinates and time. In this case the reference configuration is the configuration at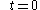 . An observer standing in the referential frame of reference observes the changes in the position and physical properties as the material body moves in space as time progresses. The results obtained are independent of the choice of initial time and reference configuration,
. An observer standing in the referential frame of reference observes the changes in the position and physical properties as the material body moves in space as time progresses. The results obtained are independent of the choice of initial time and reference configuration, 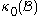 . This description is normally used in solid mechanics
. This description is normally used in solid mechanicsSolid mechanics
Solid mechanics is the branch of mechanics, physics, and mathematics that concerns the behavior of solid matter under external actions . It is part of a broader study known as continuum mechanics. One of the most common practical applications of solid mechanics is the Euler-Bernoulli beam equation...
.
In the Lagrangian description, the motion of a continuum body is expressed by the mapping function
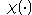 (Figure 2),
(Figure 2),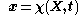
which is a mapping of the initial configuration
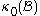 onto the current configuration
onto the current configuration 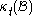 , giving a geometrical correspondence between them, i.e. giving the position vector
, giving a geometrical correspondence between them, i.e. giving the position vector 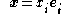 that a particle
that a particle 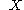 , with a position vector
, with a position vector 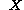 in the undeformed or reference configuration
in the undeformed or reference configuration 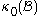 , will occupy in the current or deformed configuration
, will occupy in the current or deformed configuration 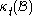 at time
at time  . The components
. The components 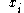 are called the spatial coordinates.
are called the spatial coordinates.Physical and kinematic properties
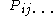 , i.e. thermodynamic properties and velocity, which describe or characterize features of the material body, are expressed as continuous functions of position and time, i.e.
, i.e. thermodynamic properties and velocity, which describe or characterize features of the material body, are expressed as continuous functions of position and time, i.e. 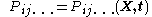 .
.The material derivative of any property
 of a continuum, which may be a scalar, vector, or tensor, is the time rate of change of that property for a specific group of particles of the moving continuum body. The material derivative is also known as the substantial derivative, or comoving derivative, or convective derivative. It can be thought as the rate at which the property changes when measured by an observer traveling with that group of particles.
of a continuum, which may be a scalar, vector, or tensor, is the time rate of change of that property for a specific group of particles of the moving continuum body. The material derivative is also known as the substantial derivative, or comoving derivative, or convective derivative. It can be thought as the rate at which the property changes when measured by an observer traveling with that group of particles.In the Lagrangian description, the material derivative of
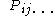 is simply the partial derivative with respect to time, and the position vector
is simply the partial derivative with respect to time, and the position vector 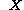 is held constant as it does not change with time. Thus, we have
is held constant as it does not change with time. Thus, we have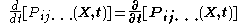
The instantaneous position
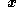 is a property of a particle, and its material derivative is the instantaneous velocity
is a property of a particle, and its material derivative is the instantaneous velocity  of the particle. Therefore, the velocity field of the continuum is given by
of the particle. Therefore, the velocity field of the continuum is given by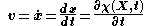
Similarly, the acceleration field is given by
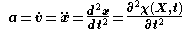
Continuity in the Lagrangian description is expressed by the spatial and temporal continuity of the mapping from the reference configuration to the current configuration of the material points. All physical quantities characterizing the continuum are described this way. In this sense, the function
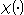 and
and  are single-valued and continuous, with continuous derivatives with respect to space and time to whatever order is required, usually to the second or third.
are single-valued and continuous, with continuous derivatives with respect to space and time to whatever order is required, usually to the second or third.Eulerian description
Continuity allows for the inverse of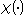 to trace backwards where the particle currently located at
to trace backwards where the particle currently located at 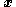 was located in the initial or referenced configuration
was located in the initial or referenced configuration 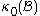 . In this case the description of motion is made in terms of the spatial coordinates, in which case is called the spatial description or Eulerian description, i.e. the current configuration is taken as the reference configuration.
. In this case the description of motion is made in terms of the spatial coordinates, in which case is called the spatial description or Eulerian description, i.e. the current configuration is taken as the reference configuration.The Eulerian description, introduced by d'Alembert, focuses on the current configuration
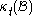 , giving attention to what is occurring at a fixed point in space as time progresses, instead of giving attention to individual particles as they move through space and time. This approach is conveniently applied in the study of fluid flow
, giving attention to what is occurring at a fixed point in space as time progresses, instead of giving attention to individual particles as they move through space and time. This approach is conveniently applied in the study of fluid flowFluid mechanics
Fluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...
where the kinematic property of greatest interest is the rate at which change is taking place rather than the shape of the body of fluid at a reference time.
Mathematically, the motion of a continuum using the Eulerian description is expressed by the mapping function
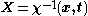
which provides a tracing of the particle which now occupies the position
 in the current configuration
in the current configuration 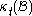 to its original position
to its original position  in the initial configuration
in the initial configuration 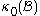 .
.A necessary and sufficient condition for this inverse function to exist is that the determinant of the Jacobian Matrix, often referred to simply as the Jacobian, should be different from zero. Thus,
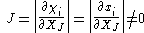
In the Eulerian description, the physical properties
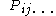 are expressed as
are expressed as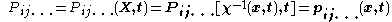
where the functional form of
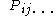 in the Lagrangian description is not the same as the form of
in the Lagrangian description is not the same as the form of 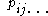 in the Eulerian description.
in the Eulerian description.The material derivative of
 , using the chain rule, is then
, using the chain rule, is then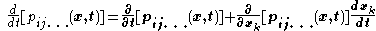
The first term on the right-hand side of this equation gives the local rate of change of the property
 occurring at position
occurring at position 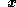 . The second term of the right-hand side is the convective rate of change and expresses the contribution of the particle changing position in space (motion).
. The second term of the right-hand side is the convective rate of change and expresses the contribution of the particle changing position in space (motion).Continuity in the Eulerian description is expressed by the spatial and temporal continuity and continuous differentiability of the velocity field. All physical quantities are defined this way at each instant of time, in the current configuration, as a function of the vector position
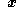 .
.Displacement field
The vector joining the positions of a particle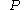 in the undeformed configuration and deformed configuration is called the displacement vector
in the undeformed configuration and deformed configuration is called the displacement vectorDisplacement (vector)
A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P...
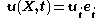 , in the Lagrangian description, or
, in the Lagrangian description, or  , in the Eulerian description.
, in the Eulerian description.A displacement field is a vector field of all displacement vectors for all particles in the body, which relates the deformed configuration with the undeformed configuration. It is convenient to do the analysis of deformation or motion of a continuum body in terms of the displacement field, In general, the displacement field is expressed in terms of the material coordinates as
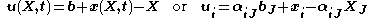
or in terms of the spatial coordinates as

where
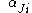 are the direction cosines between the material and spatial coordinate systems with unit vectors
are the direction cosines between the material and spatial coordinate systems with unit vectors 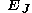 and
and 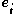 , respectively. Thus
, respectively. Thus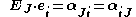
and the relationship between
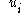 and
and 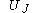 is then given by
is then given by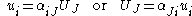
Knowing that
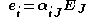
then
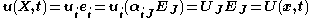
It is common to superimpose the coordinate systems for the undeformed and deformed configurations, which results in
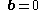 , and the direction cosines become Kronecker deltas, i.e.
, and the direction cosines become Kronecker deltas, i.e.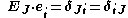
Thus, we have
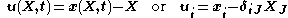
or in terms of the spatial coordinates as
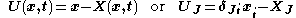
Governing equations
Continuum mechanics deals with the behavior of materials that can be approximated as continuous for certain length and time scales. The equations that govern the mechanics of such materials include the balance laws for massConservation of mass
The law of conservation of mass, also known as the principle of mass/matter conservation, states that the mass of an isolated system will remain constant over time...
, momentum, and energy
Conservation of energy
The nineteenth century law of conservation of energy is a law of physics. It states that the total amount of energy in an isolated system remains constant over time. The total energy is said to be conserved over time...
. Kinematic relations and constitutive equations are needed to complete the system of governing equations. Physical restrictions on the form of the constitutive relations can be applied by requiring that the second law of thermodynamics
Second law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
be satisfied under all conditions. In the continuum mechanics of solids, the second law of thermodynamics is satisfied if the Clausius–Duhem form of the entropy inequality is satisfied.
The balance laws express the idea that the rate of change of a quantity (mass, momentum, energy) in a volume must arise from three causes:
- the physical quantity itself flows through the surface that bounds the volume,
- there is a source of the physical quantity on the surface of the volume, or/and,
- there is a source of the physical quantity inside the volume.
Let
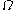 be the body (an open subset of Euclidean space) and let
be the body (an open subset of Euclidean space) and let 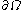 be its surface (the boundary of
be its surface (the boundary of 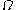 ).
).Let the motion of material points in the body be described by the map
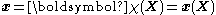
where
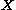 is the position of a point in the initial configuration and
is the position of a point in the initial configuration and 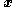 is the location of the same point in the deformed configuration.
is the location of the same point in the deformed configuration.The deformation gradient is given by
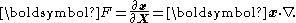
Balance laws
Let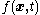 be a physical quantity that is flowing through the body. Let
be a physical quantity that is flowing through the body. Let 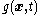 be sources on the surface of the body and let
be sources on the surface of the body and let 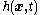 be sources inside the body. Let
be sources inside the body. Let  be the outward unit normal to the surface
be the outward unit normal to the surface  . Let
. Let 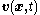 be the velocity of the physical particles that carry the physical quantity that is flowing. Also, let the speed at which the bounding surface
be the velocity of the physical particles that carry the physical quantity that is flowing. Also, let the speed at which the bounding surface  is moving be
is moving be 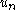 (in the direction
(in the direction  ).
).Then, balance laws can be expressed in the general form
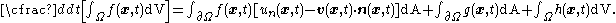
Note that the functions
 ,
, 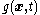 , and
, and 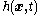 can be scalar valued, vector valued, or tensor valued - depending on the physical quantity that the balance equation deals with. If there are internal boundaries in the body, jump discontinuities also need to be specified in the balance laws.
can be scalar valued, vector valued, or tensor valued - depending on the physical quantity that the balance equation deals with. If there are internal boundaries in the body, jump discontinuities also need to be specified in the balance laws.If we take the Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
point of view, it can be shown that the balance laws of mass, momentum, and energy for a solid can be written as
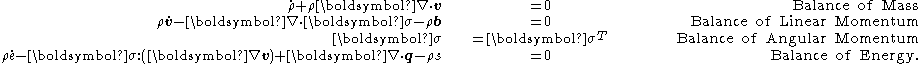
In the above equations
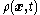 is the mass density (current),
is the mass density (current), 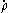 is the material time derivative of
is the material time derivative of 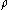 ,
, 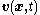 is the particle velocity,
is the particle velocity, 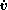 is the material time derivative of
is the material time derivative of  ,
, 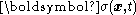 is the Cauchy stress tensor,
is the Cauchy stress tensor, 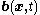 is the body force density,
is the body force density, 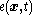 is the internal energy per unit mass,
is the internal energy per unit mass, 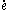 is the material time derivative of
is the material time derivative of  ,
, 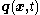 is the heat flux vector, and
is the heat flux vector, and  is an energy source per unit mass.
is an energy source per unit mass.With respect to the reference configuration, the balance laws can be written as
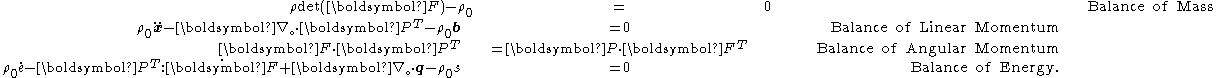
In the above,
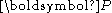 is the first Piola-Kirchhoff stress tensor, and
is the first Piola-Kirchhoff stress tensor, and 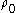 is the mass density in the reference configuration. The first Piola-Kirchhoff stress tensor is related to the Cauchy stress tensor by
is the mass density in the reference configuration. The first Piola-Kirchhoff stress tensor is related to the Cauchy stress tensor by
We can alternatively define the nominal stress tensor
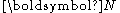 which is the transpose of the first Piola-Kirchhoff stress tensor such that
which is the transpose of the first Piola-Kirchhoff stress tensor such that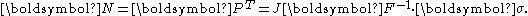
Then the balance laws become
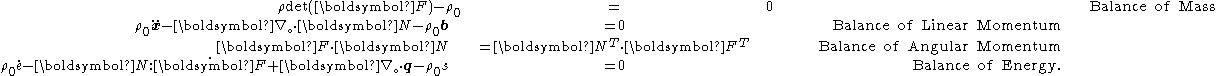
The operators in the above equations are defined as such that
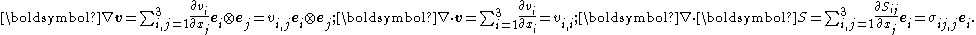
where
 is a vector field,
is a vector field, 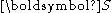 is a second-order tensor field, and
is a second-order tensor field, and 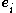 are the components of an orthonormal basis in the current configuration. Also,
are the components of an orthonormal basis in the current configuration. Also,
where
 is a vector field,
is a vector field,  is a second-order tensor field, and
is a second-order tensor field, and 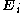 are the components of an orthonormal basis in the reference configuration.
are the components of an orthonormal basis in the reference configuration.The inner product is defined as
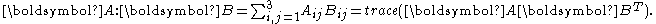
The Clausius–Duhem inequality
The Clausius–Duhem inequality can be used to express the second law of thermodynamics for elastic-plastic materials. This inequality is a statement concerning the irreversibility of natural processes, especially when energy dissipation is involved.Just like in the balance laws in the previous section, we assume that there is a flux of a quantity, a source of the quantity, and an internal density of the quantity per unit mass. The quantity of interest in this case is the entropy. Thus, we assume that there is an entropy flux, an entropy source, and an internal entropy density per unit mass (
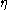 ) in the region of interest.
) in the region of interest.Let
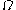 be such a region and let
be such a region and let  be its boundary. Then the second law of thermodynamics states that the rate of increase of
be its boundary. Then the second law of thermodynamics states that the rate of increase of 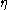 in this region is greater than or equal to the sum of that supplied to
in this region is greater than or equal to the sum of that supplied to 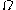 (as a flux or from internal sources) and the change of the internal entropy density due to material flowing in and out of the region.
(as a flux or from internal sources) and the change of the internal entropy density due to material flowing in and out of the region.Let
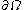 move with a velocity
move with a velocity 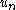 and let particles inside
and let particles inside 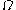 have velocities
have velocities  . Let
. Let  be the unit outward normal to the surface
be the unit outward normal to the surface 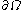 . Let
. Let 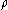 be the density of matter in the region,
be the density of matter in the region, 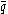 be the entropy flux at the surface, and
be the entropy flux at the surface, and  be the entropy source per unit mass.
be the entropy source per unit mass.Then the entropy inequality may be written as
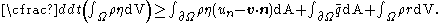
The scalar entropy flux can be related to the vector flux at the surface by the relation
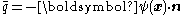 . Under the assumption of incrementally isothermal conditions, we have
. Under the assumption of incrementally isothermal conditions, we have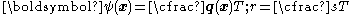
where
 is the heat flux vector,
is the heat flux vector,  is a energy source per unit mass, and
is a energy source per unit mass, and  is the absolute temperature of a material point at
is the absolute temperature of a material point at  at time
at time  .
.We then have the Clausius–Duhem inequality in integral form:

We can show that the entropy inequality may be written in differential form as

In terms of the Cauchy stress and the internal energy, the Clausius–Duhem inequality may be written as
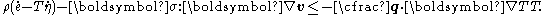
Applications
- MechanicsMechanicsMechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
- Solid mechanicsSolid mechanicsSolid mechanics is the branch of mechanics, physics, and mathematics that concerns the behavior of solid matter under external actions . It is part of a broader study known as continuum mechanics. One of the most common practical applications of solid mechanics is the Euler-Bernoulli beam equation...
- Fluid mechanicsFluid mechanicsFluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...
- Solid mechanics
- EngineeringEngineeringEngineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
- Mechanical engineeringMechanical engineeringMechanical engineering is a discipline of engineering that applies the principles of physics and materials science for analysis, design, manufacturing, and maintenance of mechanical systems. It is the branch of engineering that involves the production and usage of heat and mechanical power for the...
- Civil engineeringCivil engineeringCivil engineering is a professional engineering discipline that deals with the design, construction, and maintenance of the physical and naturally built environment, including works like roads, bridges, canals, dams, and buildings...
- Aerospace engineeringAerospace engineeringAerospace engineering is the primary branch of engineering concerned with the design, construction and science of aircraft and spacecraft. It is divided into two major and overlapping branches: aeronautical engineering and astronautical engineering...
- Mechanical engineering
See also
- Finite deformation tensorsFinite deformation tensorsIn continuum mechanics, the finite strain theory—also called large strain theory, or large deformation theory—deals with deformations in which both rotations and strains are arbitrarily large, i.e. invalidates the assumptions inherent in infinitesimal strain theory...
- Finite strain theory
- Stress (physics)Stress (physics)In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
- Stress measuresStress measuresThe most commonly used measure of stress is the Cauchy stress. However, several other measures of stress can be defined. Some such stress measures that are widely used in continuum mechanics, particularly in the computational context, are:...
- Hyperelastic materialHyperelastic materialA hyperelastic or Green elastic material is a type of constitutive model for ideally elastic material for which the stress-strain relationship derives from a strain energy density function. The hyperelastic material is a special case of a Cauchy elastic material.For many materials, linear elastic...
- Cauchy elastic materialCauchy elastic materialA Cauchy-elastic material is one in which the Cauchy stress at each material point is determined only by the current state of deformation . A Cauchy-elastic material is one in which the Cauchy stress at each material point is determined only by the current state of deformation (with respect to an...
- Equation of stateEquation of stateIn physics and thermodynamics, an equation of state is a relation between state variables. More specifically, an equation of state is a thermodynamic equation describing the state of matter under a given set of physical conditions...
- Theory of elasticity
- Bernoulli's principleBernoulli's principleIn fluid dynamics, Bernoulli's principle states that for an inviscid flow, an increase in the speed of the fluid occurs simultaneously with a decrease in pressure or a decrease in the fluid's potential energy...
- PeridynamicsPeridynamicsPeridynamics is a formulation of continuum mechanics that is oriented toward deformations with discontinuities, especially fractures.-Purpose of peridynamics:...
(a non-local continuum theory leading to integral equations) - Tensor calculus
- Curvilinear coordinatesCurvilinear coordinatesCurvilinear coordinates are a coordinate system for Euclidean space in which the coordinate lines may be curved. These coordinates may be derived from a set of Cartesian coordinates by using a transformation that is locally invertible at each point. This means that one can convert a point given...
- Tensor derivative (continuum mechanics)Tensor derivative (continuum mechanics)The derivatives of scalars, vectors, and second-order tensors with respect to second-order tensors are of considerable use in continuum mechanics. These derivatives are used in the theories of nonlinear elasticity and plasticity, particularly in the design of algorithms for numerical...
- Movable cellular automatonMovable cellular automatonThe Movable cellular automaton method is a method in computational solid mechanics based on the discrete concept. It provides advantages both of classical cellular automaton and discrete element methods. Important advantage of the МСА method is a possibility of direct simulation of materials...

