Displacement current
Encyclopedia
In electromagnetism
, displacement current is a quantity that is defined in terms of the rate of change of electric displacement field. Displacement current has the units of electric current density
, and it has an associated magnetic field
just as actual currents do. However it is not an electric current of moving charges
, but a time-varying electric field
. In materials, there is also a contribution from the slight motion of charges bound in atoms, dielectric polarization.
The idea was conceived by James Clerk Maxwell
in his 1861 paper On Physical Lines of Force in connection with the displacement of electric particles in a dielectric
medium. Maxwell added displacement current to the electric current
term in Ampère's Circuital Law. In his 1865 paper A Dynamical Theory of the Electromagnetic Field
Maxwell used this amended version of Ampère's Circuital Law to derive the electromagnetic wave equation
. This derivation is now generally accepted as an historical landmark in physics by virtue of uniting electricity, magnetism and optics into one single unified theory. The displacement current term is now seen as a crucial addition that completed Maxwell's equations and is necessary to explain many phenomena, most particularly the existence of electromagnetic waves.
where:
Differentiating this equation with respect to time defines the displacement current, which therefore has two components in a dielectric
:
The first term on the right hand side is present in material media and in free space. It doesn't necessarily involve any actual movement of charge, but it does have an associated magnetic field, just as does a current due to charge motion. Some authors apply the name displacement current to only this contribution.
The second term on the right hand side is associated with the polarization of the individual molecules of the dielectric material. Polarization results when the charges in molecules move a little under the influence of an applied electric field
. The positive and negative charges in molecules separate, causing an increase in the state of polarization P. A changing state of polarization corresponds to charge movement and so is equivalent to a current.
This polarization is the displacement current as it was originally conceived by Maxwell. Maxwell made no special treatment of the vacuum, treating it as a material medium. For Maxwell, the effect of P was simply to change the relative permittivity εr in the relation D = εrε0 E.
The modern justification of displacement current is explained below.
where the permittivity
ε = ε0 εr,
In this equation the use of ε, accounts for
the polarization of the dielectric.
The scalar
value of displacement current may also be expressed in terms of electric flux:
The forms in terms of ε are correct only for linear isotropic materials. More generally ε may be replaced by a tensor
, may depend upon the electric field itself, and may exhibit time dependence (dispersion).
For a linear isotropic dielectric, the polarization P is given by:
where χe is known as the electric susceptibility
of the dielectric. Note that:
:
where
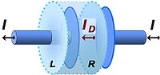
The magnetic field between the plates is the same as that outside the plates, so the displacement current must be the same as the conduction current in the wires, that is,
which extends the notion of current beyond a mere transport of charge.
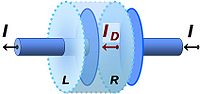
Next, this displacement current is related to the charging of the capacitor. Consider the current in the imaginary cylindrical surface shown surrounding the left plate. A current, say I, passes outward through the left surface L of the cylinder, but no conduction current (no transport of real charges) enters the right surface R. Notice that the electric field between the plates E increases as the capacitor charges. That is, in a manner described by Gauss's law
, assuming no dielectric between the plates:
where S refers to the imaginary cylindrical surface. Assuming a parallel plate capacitor with uniform electric field, and neglecting fringing effects around the edges of the plates, differentiation provides:
where the sign is negative because charge leaves this plate (the charge is decreasing), and where S is the area of the face R. The electric field at face L is zero because the field due to charge on the right-hand plate is terminated by the equal but opposite charge on the left-hand plate. Under the assumption of a uniform electric field distribution inside the capacitor, the displacement current density JD is found by dividing by the area of the surface:
where I is the current leaving the cylindrical surface (which must equal −ID as the two currents sum to zero) and JD is the flow of charge per unit area into the cylindrical surface through the face R.
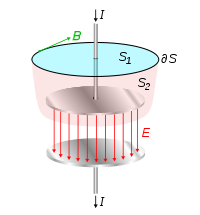Combining these results, the magnetic field is found using the integral form of Ampère's law
with an arbitrary choice of contour provided the displacement current density term is added to the conduction current density (the Ampère-Maxwell equation):
This equation says that the integral of the magnetic field B around a loop ∂S is equal to the integrated current J through any surface spanning the loop, plus the displacement current term ε0 ∂E / ∂t through the surface. Applying the Ampère-Maxwell equation to surface S1 we find:
However, applying this law to surface S2, which is bounded by exactly the same curve
, but lies between the plates, provides:
Any surface that intersects the wire has current I passing through it so Ampère's law
gives the correct magnetic field. Also, any surface bounded by the same loop but passing between the capacitor's plates has no charge transport flowing through it, but the ε0 ∂E / ∂t term provides a second source for the magnetic field besides charge conduction current. Because the current is increasing the charge on the capacitor's plates, the electric field between the plates is increasing, and the rate of change of electric field gives the correct value for the field B found above.
The current leaving a volume must equal the rate of decrease of charge in a volume. In differential form this continuity equation becomes:
where the left side is the divergence of the free current density and the right side is the rate of decrease of the free charge density. However, Ampère's law
in its original form states:
which implies that the divergence of the current term vanishes, contradicting the continuity equation. (Vanishing of the divergence is a result of the mathematical identity that states the divergence of a curl is always zero.) This conflict is removed by addition of the displacement current, as then:
and
which is in agreement with the continuity equation because of Gauss's law
:
Substituting this form for J into Ampère's law
, and assuming there is no bound or free current density contributing to J :
with the result:
However,
leading to the wave equation
:
where use is made of the vector identity that holds for any vector field V(r, t):
and the fact that the divergence of the magnetic field is zero. An identical wave equation can be found for the electric field by taking the curl:
If J, P and ρ are zero, the result is:
The electric field can be expressed in the general form:
where φ is the electric potential
(which can be chosen to satisfy Poisson's equation
) and A is a vector potential
. The ∇φ component on the right hand side is the Gauss's law component, and this is the component that is relevant to the conservation of charge argument above. The second term on the right-hand side is the one relevant to the electromagnetic wave equation, because it is the term that contributes to the curl of E. Because of the vector identity that says the curl of a gradient is zero, ∇φ does not contribute to ∇×E.
Maxwell's purpose is stated by him at (Part I, p. 161):
He is careful to point out the treatment is one of analogy:
In part III, in relation to displacement current, he says
Clearly Maxwell was driving at magnetization even though the same introduction clearly talks about dielectric polarization.
Maxwell concluded, using Newton's equation for the speed of sound (Lines of Force, Part III, equation (132)), that “light consists of transverse undulations in the same medium that is the cause of electric and magnetic phenomena.”
But although the above quotations point towards a magnetic explanation for displacement current, for example, based upon the divergence of the above curl equation, Maxwell's explanation ultimately stressed linear polarization of dielectrics:
With some change of symbols (and units): r → J, R → −E and the material constant E−2 → 4π εrε0 these equations take the familiar form:
When it came to deriving the electromagnetic wave equation from displacement current in his 1865 paper A Dynamical Theory of the Electromagnetic Field
, he got around the problem of the non-zero divergence associated with Gauss's law and dielectric displacement by eliminating the Gauss term and deriving the wave equation exclusively for the solenoidal magnetic field vector.
Maxwell's emphasis on polarization diverted attention towards the electric capacitor circuit, and led to the common belief that Maxwell conceived of displacement current so as to maintain conservation of charge in an electric capacitor circuit. There are a variety of debatable notions about Maxwell's thinking, ranging from his supposed desire to perfect the symmetry of the field equations to the desire to achieve compatibility with the continuity equation.
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
, displacement current is a quantity that is defined in terms of the rate of change of electric displacement field. Displacement current has the units of electric current density
Current density
Current density is a measure of the density of flow of a conserved charge. Usually the charge is the electric charge, in which case the associated current density is the electric current per unit area of cross section, but the term current density can also be applied to other conserved...
, and it has an associated magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
just as actual currents do. However it is not an electric current of moving charges
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
, but a time-varying electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
. In materials, there is also a contribution from the slight motion of charges bound in atoms, dielectric polarization.
The idea was conceived by James Clerk Maxwell
James Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
in his 1861 paper On Physical Lines of Force in connection with the displacement of electric particles in a dielectric
Dielectric
A dielectric is an electrical insulator that can be polarized by an applied electric field. When a dielectric is placed in an electric field, electric charges do not flow through the material, as in a conductor, but only slightly shift from their average equilibrium positions causing dielectric...
medium. Maxwell added displacement current to the electric current
Electric current
Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire...
term in Ampère's Circuital Law. In his 1865 paper A Dynamical Theory of the Electromagnetic Field
A Dynamical Theory of the Electromagnetic Field
"A Dynamical Theory of the Electromagnetic Field" is the third of James Clerk Maxwell's papers regarding electromagnetism, published in 1865. It is the paper in which the original set of four Maxwell's equations first appeared...
Maxwell used this amended version of Ampère's Circuital Law to derive the electromagnetic wave equation
Electromagnetic wave equation
The electromagnetic wave equation is a second-order partial differential equation that describes the propagation of electromagnetic waves through a medium or in a vacuum...
. This derivation is now generally accepted as an historical landmark in physics by virtue of uniting electricity, magnetism and optics into one single unified theory. The displacement current term is now seen as a crucial addition that completed Maxwell's equations and is necessary to explain many phenomena, most particularly the existence of electromagnetic waves.
Explanation
The electric displacement field is defined as:where:
- ε0 is the permittivityPermittivityIn electromagnetism, absolute permittivity is the measure of the resistance that is encountered when forming an electric field in a medium. In other words, permittivity is a measure of how an electric field affects, and is affected by, a dielectric medium. The permittivity of a medium describes how...
of free space - E is the electric field intensity
- P is the polarization of the medium
Differentiating this equation with respect to time defines the displacement current, which therefore has two components in a dielectric
Dielectric
A dielectric is an electrical insulator that can be polarized by an applied electric field. When a dielectric is placed in an electric field, electric charges do not flow through the material, as in a conductor, but only slightly shift from their average equilibrium positions causing dielectric...
:
The first term on the right hand side is present in material media and in free space. It doesn't necessarily involve any actual movement of charge, but it does have an associated magnetic field, just as does a current due to charge motion. Some authors apply the name displacement current to only this contribution.
The second term on the right hand side is associated with the polarization of the individual molecules of the dielectric material. Polarization results when the charges in molecules move a little under the influence of an applied electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
. The positive and negative charges in molecules separate, causing an increase in the state of polarization P. A changing state of polarization corresponds to charge movement and so is equivalent to a current.
This polarization is the displacement current as it was originally conceived by Maxwell. Maxwell made no special treatment of the vacuum, treating it as a material medium. For Maxwell, the effect of P was simply to change the relative permittivity εr in the relation D = εrε0 E.
The modern justification of displacement current is explained below.
Isotropic dielectric case
In the case of a very simple dielectric material the constitutive relation holds:where the permittivity
Permittivity
In electromagnetism, absolute permittivity is the measure of the resistance that is encountered when forming an electric field in a medium. In other words, permittivity is a measure of how an electric field affects, and is affected by, a dielectric medium. The permittivity of a medium describes how...
ε = ε0 εr,
- εr is the relative permittivity of the dielectric and
- ε0 is the electric constantElectric constantThe physical constant ε0, commonly called the vacuum permittivity, permittivity of free space or electric constant is an ideal, physical constant, which is the value of the absolute dielectric permittivity of classical vacuum...
.
In this equation the use of ε, accounts for
the polarization of the dielectric.
The scalar
Scalar (physics)
In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations , or by Lorentz transformations or space-time translations . This is in contrast to a vector...
value of displacement current may also be expressed in terms of electric flux:
The forms in terms of ε are correct only for linear isotropic materials. More generally ε may be replaced by a tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
, may depend upon the electric field itself, and may exhibit time dependence (dispersion).
For a linear isotropic dielectric, the polarization P is given by:
where χe is known as the electric susceptibility
Electric susceptibility
In electromagnetism, the electric susceptibility \chi_e is a dimensionless proportionality constant that indicates the degree of polarization of a dielectric material in response to an applied electric field...
of the dielectric. Note that:
Necessity
Some implications of the displacement current follow, which agree with experimental observation, and with the requirements of logical consistency for the theory of electromagnetism.Current in capacitors
An example illustrating the need for the displacement current arises in connection with capacitors with no medium between the plates. Consider the charging capacitor in the figure. The capacitor is in a circuit that transfers charge (on a wire external to the capacitor) from the left plate to the right plate, charging the capacitor and increasing the electric field between its plates. The same current enters the right plate (say I ) as leaves the left plate. Although current is flowing through the capacitor, no actual charge is transported through the vacuum between its plates. Nonetheless, a magnetic field exists between the plates as though a current were present there as well. The explanation is that a displacement current ID flows in the vacuum, and this current produces the magnetic field in the region between the plates according to Ampère's lawAmpère's law
In classical electromagnetism, Ampère's circuital law, discovered by André-Marie Ampère in 1826, relates the integrated magnetic field around a closed loop to the electric current passing through the loop...
:
where
is the closed line integralLine integralIn mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...
around some closed curve C.
is the magnetic fieldMagnetic fieldA magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
in teslaTesla (unit)The tesla is the SI derived unit of magnetic field B . One tesla is equal to one weber per square meter, and it was defined in 1960 in honour of the inventor, physicist, and electrical engineer Nikola Tesla...
.-
is the vector dot productDot productIn mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
. 
is an infinitesimalInfinitesimalInfinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
element (differentialDifferential (mathematics)In mathematics, the term differential has several meanings.-Basic notions:* In calculus, the differential represents a change in the linearization of a function....
) of the curve C (that is, a vector with magnitude equal to the length of the infinitesimal line element, and direction given by the tangent to the curve C).
is the magnetic constant also called the permeability of free space.
is the net displacement current that links the curve C.
The magnetic field between the plates is the same as that outside the plates, so the displacement current must be the same as the conduction current in the wires, that is,
which extends the notion of current beyond a mere transport of charge.
Next, this displacement current is related to the charging of the capacitor. Consider the current in the imaginary cylindrical surface shown surrounding the left plate. A current, say I, passes outward through the left surface L of the cylinder, but no conduction current (no transport of real charges) enters the right surface R. Notice that the electric field between the plates E increases as the capacitor charges. That is, in a manner described by Gauss's law
Gauss's law
In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:...
, assuming no dielectric between the plates:
where S refers to the imaginary cylindrical surface. Assuming a parallel plate capacitor with uniform electric field, and neglecting fringing effects around the edges of the plates, differentiation provides:
where the sign is negative because charge leaves this plate (the charge is decreasing), and where S is the area of the face R. The electric field at face L is zero because the field due to charge on the right-hand plate is terminated by the equal but opposite charge on the left-hand plate. Under the assumption of a uniform electric field distribution inside the capacitor, the displacement current density JD is found by dividing by the area of the surface:
where I is the current leaving the cylindrical surface (which must equal −ID as the two currents sum to zero) and JD is the flow of charge per unit area into the cylindrical surface through the face R.
Ampère's law
In classical electromagnetism, Ampère's circuital law, discovered by André-Marie Ampère in 1826, relates the integrated magnetic field around a closed loop to the electric current passing through the loop...
with an arbitrary choice of contour provided the displacement current density term is added to the conduction current density (the Ampère-Maxwell equation):
This equation says that the integral of the magnetic field B around a loop ∂S is equal to the integrated current J through any surface spanning the loop, plus the displacement current term ε0 ∂E / ∂t through the surface. Applying the Ampère-Maxwell equation to surface S1 we find:
However, applying this law to surface S2, which is bounded by exactly the same curve
, but lies between the plates, provides:Any surface that intersects the wire has current I passing through it so Ampère's law
Ampère's law
In classical electromagnetism, Ampère's circuital law, discovered by André-Marie Ampère in 1826, relates the integrated magnetic field around a closed loop to the electric current passing through the loop...
gives the correct magnetic field. Also, any surface bounded by the same loop but passing between the capacitor's plates has no charge transport flowing through it, but the ε0 ∂E / ∂t term provides a second source for the magnetic field besides charge conduction current. Because the current is increasing the charge on the capacitor's plates, the electric field between the plates is increasing, and the rate of change of electric field gives the correct value for the field B found above.
Mathematical formulation
In a more mathematical vein, the same results can be obtained from the underlying differential equations. Consider for simplicity a non-magnetic medium where the relative magnetic permeability is unity, and the complication of magnetization current is absent.The current leaving a volume must equal the rate of decrease of charge in a volume. In differential form this continuity equation becomes:
where the left side is the divergence of the free current density and the right side is the rate of decrease of the free charge density. However, Ampère's law
Ampère's law
In classical electromagnetism, Ampère's circuital law, discovered by André-Marie Ampère in 1826, relates the integrated magnetic field around a closed loop to the electric current passing through the loop...
in its original form states:
which implies that the divergence of the current term vanishes, contradicting the continuity equation. (Vanishing of the divergence is a result of the mathematical identity that states the divergence of a curl is always zero.) This conflict is removed by addition of the displacement current, as then:
and
which is in agreement with the continuity equation because of Gauss's law
Gauss's law
In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:...
:
Wave propagation
The added displacement current also leads to wave propagation by taking the curl of the equation for magnetic field.Substituting this form for J into Ampère's law
Ampère's law
In classical electromagnetism, Ampère's circuital law, discovered by André-Marie Ampère in 1826, relates the integrated magnetic field around a closed loop to the electric current passing through the loop...
, and assuming there is no bound or free current density contributing to J :
with the result:
However,
leading to the wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
:
where use is made of the vector identity that holds for any vector field V(r, t):
and the fact that the divergence of the magnetic field is zero. An identical wave equation can be found for the electric field by taking the curl:
If J, P and ρ are zero, the result is:
The electric field can be expressed in the general form:
where φ is the electric potential
Electric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
(which can be chosen to satisfy Poisson's equation
Poisson's equation
In mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in electrostatics, mechanical engineering and theoretical physics...
) and A is a vector potential
Magnetic potential
The term magnetic potential can be used for either of two quantities in classical electromagnetism: the magnetic vector potential, A, and the magnetic scalar potential, ψ...
. The ∇φ component on the right hand side is the Gauss's law component, and this is the component that is relevant to the conservation of charge argument above. The second term on the right-hand side is the one relevant to the electromagnetic wave equation, because it is the term that contributes to the curl of E. Because of the vector identity that says the curl of a gradient is zero, ∇φ does not contribute to ∇×E.
History and interpretation
Maxwell's displacement current was postulated in part III of his 1861 paper 'On Physical Lines of Force'. Few topics in modern physics have caused as much confusion and misunderstanding as that of displacement current. This is in part due to the fact that Maxwell used a sea of molecular vortices in his derivation, while modern textbooks operate on the basis that displacement current can exist in free space. Maxwell's derivation is unrelated to the modern day derivation for displacement current in the vacuum, which is based on consistency between Ampère's law for the magnetic field and the continuity equation for electric charge.Maxwell's purpose is stated by him at (Part I, p. 161):
He is careful to point out the treatment is one of analogy:
In part III, in relation to displacement current, he says
Clearly Maxwell was driving at magnetization even though the same introduction clearly talks about dielectric polarization.
Maxwell concluded, using Newton's equation for the speed of sound (Lines of Force, Part III, equation (132)), that “light consists of transverse undulations in the same medium that is the cause of electric and magnetic phenomena.”
But although the above quotations point towards a magnetic explanation for displacement current, for example, based upon the divergence of the above curl equation, Maxwell's explanation ultimately stressed linear polarization of dielectrics:
With some change of symbols (and units): r → J, R → −E and the material constant E−2 → 4π εrε0 these equations take the familiar form:
When it came to deriving the electromagnetic wave equation from displacement current in his 1865 paper A Dynamical Theory of the Electromagnetic Field
A Dynamical Theory of the Electromagnetic Field
"A Dynamical Theory of the Electromagnetic Field" is the third of James Clerk Maxwell's papers regarding electromagnetism, published in 1865. It is the paper in which the original set of four Maxwell's equations first appeared...
, he got around the problem of the non-zero divergence associated with Gauss's law and dielectric displacement by eliminating the Gauss term and deriving the wave equation exclusively for the solenoidal magnetic field vector.
Maxwell's emphasis on polarization diverted attention towards the electric capacitor circuit, and led to the common belief that Maxwell conceived of displacement current so as to maintain conservation of charge in an electric capacitor circuit. There are a variety of debatable notions about Maxwell's thinking, ranging from his supposed desire to perfect the symmetry of the field equations to the desire to achieve compatibility with the continuity equation.
Maxwell's papers
- On Faraday's Lines of Force Maxwell's paper of 1855
- On Physical Lines of Force Maxwell's paper of 1861
- A Dynamical Theory of the Electromagnetic Field Maxwell's paper of 1864
Further reading
- AM Bork Maxwell, Displacement Current, and Symmetry (1963)
- AM Bork Maxwell and the Electromagnetic Wave Equation (1967)
See also
- Electromagnetic wave equationElectromagnetic wave equationThe electromagnetic wave equation is a second-order partial differential equation that describes the propagation of electromagnetic waves through a medium or in a vacuum...
- Ampère's lawAmpère's lawIn classical electromagnetism, Ampère's circuital law, discovered by André-Marie Ampère in 1826, relates the integrated magnetic field around a closed loop to the electric current passing through the loop...
- Capacitance