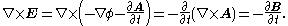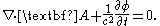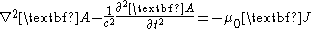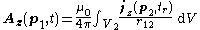Magnetic potential
Encyclopedia
The term magnetic potential can be used for either of two quantities in classical electromagnetism
: the magnetic vector potential, A, (often simply called the vector potential) and the magnetic scalar potential, ψ. Both quantities can be used in certain circumstances to calculate the magnetic field
.
The more frequently used magnetic vector potential A (often simply called the vector potential) is defined such that the curl of A is the magnetic B field. Together with the electric potential, the magnetic vector potential can be used to specify the electric field
, E as well. Therefore, many equations of electromagnetism can be written either in terms of the E and B, or in terms of the magnetic vector potential and electric potential. In more advanced theories such as quantum mechanics
, most equations use the potentials and not the E and B fields.
The magnetic scalar potential ψ is sometimes used to specify the magnetic H-field in cases when there are no free currents, in a manner analogous to using the electric potential
to determine the electric field
in electrostatics
. One important use of ψ is to determine the magnetic field due to permanent magnets when their magnetization
is known. With some care the scalar potential can be extended to include free currents as well.
that together with the (scalar field) electric potential
φ are defined as:
where B is the magnetic field
and E is the electric field. In magnetostatics where there is no time varying charge distribution, only the first equation is needed. (In the context of electrodynamics, the terms "vector potential" and "scalar potential" are used for "magnetic vector potential" and "electric potential
", respectively. In mathematics, vector potential
and scalar potential
have more general meanings.)
Defining the electric and magnetic fields from potentials automatically satisfies two of Maxwell's equations
: Gauss's law for magnetism and Faraday's Law
. For example, if A is continuous and well-defined everywhere, then it is guaranteed not to result in magnetic monopoles. (In the mathematical theory of magnetic monopoles, A is allowed to be either undefined or multiple-valued in some places; see magnetic monopole
for details.)
Starting with the above definitions:
Alternatively, the existence of A and φ is guaranteed from these two laws using the Helmholtz's theorem
. For example, since the magnetic field is divergence
-free (Gauss's law for magnetism), i.e. , A always exists that satisfies the above definition.
The vector potential A is used when studying the Lagrangian
in classical mechanics
and in quantum mechanics
(see Schrödinger equation for charged particles
, Dirac equation
, Aharonov-Bohm effect
).
In the SI system, the units of A are volt
-second
s per metre
(V·s·m−1) and are the same as that of momentum per unit charge.
Although the magnetic field B is a pseudovector
(also called axial vector), the vector potential A is not: A is a polar vector. This means that if the right-hand rule
for cross product
s were replaced with a left-hand rule, but without changing any other equations or definitions, then B would switch signs, but A would not change. This is an example of a general theorem: The curl of a polar vector is a pseudovector, and vice-versa.
available when choosing A. This condition is known as gauge invariance.
Using the Lorenz gauge, Maxwell's equations
can be written compactly in terms of the magnetic vector potential A and the electric scalar potential
Φ.
In other gauges
, the equations are different. A different notation to write these same equations (using four-vectors) is shown below.
There are a few notable things about A and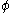
calculated in this way:
In other gauges the formula for A and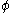
is different—for example, see Coulomb gauge for another possibility.
Since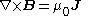
(assuming quasi-static conditions, i.e. 
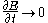)and 
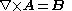, the lines and contours of A relate to B like the lines and contours of B relate to j. Thus, a depiction of the A field around a loop of B flux (as would be produced in a toroidal inductor) is qualitatively the same as the B field around a loop of current.
The figure to the left is an artist's depiction of the A field. The thicker lines indicate paths of higher average intensity (shorter paths have higher intensity so that the path integral is the same). The lines are just drawn to look good and impart general look of the A field.
The drawing tacitly assumes
. This would be true under the following assumptions:
, it is natural to join the magnetic vector potential together with the (scalar) electric potential
into the electromagnetic potential, also called "four-potential".
One motivation for doing so is that the four-potential is a mathematical four-vector
. Thus, using standard four-vector transformation rules, if the electric and magnetic potentials are known in one inertial reference frame, they can be simply calculated in any other inertial reference frame.
Another, related motivation is that the content of classical electromagnetism can be written in a concise and convenient form using the electromagnetic four potential, especially when the Lorenz gauge is used. In particular, in abstract index notation
, the set of Maxwell's equations
(in the Lorenz gauge) may be written (in Gaussian units
) as follows:
where □ is the d'Alembertian and J is the four-current
. The first equation is the Lorenz gauge condition
while the second contains Maxwell's equations.
Yet another motivation for creating the electromagnetic four-potential is that it plays a very important role in quantum electrodynamics
.
is another useful tool in describing the magnetic field, especially for permanent magnets.
In a simply connected domain where there is no free current,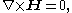
hence we can define magnetic scalar potential ψ as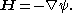
And since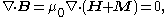
it follows that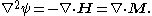
Here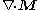
acts as the source for magnetic field, much like 
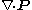as the source for electric field. So analogously to bound electric charge, we can call
bound magnetic charge.
If there is free current, one may subtract the contribution of free current per Biot-Savart law
from total magnetic field and solve the remainder with the scalar potential method.
Classical electromagnetism
Classical electromagnetism is a branch of theoretical physics that studies consequences of the electromagnetic forces between electric charges and currents...
: the magnetic vector potential, A, (often simply called the vector potential) and the magnetic scalar potential, ψ. Both quantities can be used in certain circumstances to calculate the magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
.
The more frequently used magnetic vector potential A (often simply called the vector potential) is defined such that the curl of A is the magnetic B field. Together with the electric potential, the magnetic vector potential can be used to specify the electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
, E as well. Therefore, many equations of electromagnetism can be written either in terms of the E and B, or in terms of the magnetic vector potential and electric potential. In more advanced theories such as quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, most equations use the potentials and not the E and B fields.
The magnetic scalar potential ψ is sometimes used to specify the magnetic H-field in cases when there are no free currents, in a manner analogous to using the electric potential
Electric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
to determine the electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
in electrostatics
Electrostatics
Electrostatics is the branch of physics that deals with the phenomena and properties of stationary or slow-moving electric charges....
. One important use of ψ is to determine the magnetic field due to permanent magnets when their magnetization
Magnetization
In classical electromagnetism, magnetization or magnetic polarization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material...
is known. With some care the scalar potential can be extended to include free currents as well.
Magnetic vector potential
The magnetic vector potential A is a vector fieldVector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
that together with the (scalar field) electric potential
Electric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
φ are defined as:
where B is the magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
and E is the electric field. In magnetostatics where there is no time varying charge distribution, only the first equation is needed. (In the context of electrodynamics, the terms "vector potential" and "scalar potential" are used for "magnetic vector potential" and "electric potential
Electric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
", respectively. In mathematics, vector potential
Vector potential
In vector calculus, a vector potential is a vector field whose curl is a given vector field. This is analogous to a scalar potential, which is a scalar field whose negative gradient is a given vector field....
and scalar potential
Scalar potential
A scalar potential is a fundamental concept in vector analysis and physics . The scalar potential is an example of a scalar field...
have more general meanings.)
Defining the electric and magnetic fields from potentials automatically satisfies two of Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
: Gauss's law for magnetism and Faraday's Law
Faraday's law of induction
Faraday's law of induction dates from the 1830s, and is a basic law of electromagnetism relating to the operating principles of transformers, inductors, and many types of electrical motors and generators...
. For example, if A is continuous and well-defined everywhere, then it is guaranteed not to result in magnetic monopoles. (In the mathematical theory of magnetic monopoles, A is allowed to be either undefined or multiple-valued in some places; see magnetic monopole
Magnetic monopole
A magnetic monopole is a hypothetical particle in particle physics that is a magnet with only one magnetic pole . In more technical terms, a magnetic monopole would have a net "magnetic charge". Modern interest in the concept stems from particle theories, notably the grand unified and superstring...
for details.)
Starting with the above definitions:
Alternatively, the existence of A and φ is guaranteed from these two laws using the Helmholtz's theorem
Helmholtz decomposition
In physics and mathematics, in the area of vector calculus, Helmholtz's theorem, also known as the fundamental theorem of vector calculus, states that any sufficiently smooth, rapidly decaying vector field in three dimensions can be resolved into the sum of an irrotational vector field and a...
. For example, since the magnetic field is divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
-free (Gauss's law for magnetism), i.e. , A always exists that satisfies the above definition.
The vector potential A is used when studying the Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
in classical mechanics
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
and in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
(see Schrödinger equation for charged particles
Pauli equation
The Pauli equation, also known as the Schrödinger–Pauli equation, is the formulation of the Schrödinger equation for spin- particles which takes into account the interaction of the particle's spin with the electromagnetic field...
, Dirac equation
Dirac equation
The Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
, Aharonov-Bohm effect
Aharonov-Bohm effect
The Aharonov–Bohm effect, sometimes called the Ehrenberg–Siday–Aharonov–Bohm effect, is a quantum mechanical phenomenon in which an electrically charged particle is affected by an electromagnetic field , despite being confined to a region in which both the magnetic field B and electric field E are...
).
In the SI system, the units of A are volt
Volt
The volt is the SI derived unit for electric potential, electric potential difference, and electromotive force. The volt is named in honor of the Italian physicist Alessandro Volta , who invented the voltaic pile, possibly the first chemical battery.- Definition :A single volt is defined as the...
-second
Second
The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....
s per metre
Metre
The metre , symbol m, is the base unit of length in the International System of Units . Originally intended to be one ten-millionth of the distance from the Earth's equator to the North Pole , its definition has been periodically refined to reflect growing knowledge of metrology...
(V·s·m−1) and are the same as that of momentum per unit charge.
Although the magnetic field B is a pseudovector
Pseudovector
In physics and mathematics, a pseudovector is a quantity that transforms like a vector under a proper rotation, but gains an additional sign flip under an improper rotation such as a reflection. Geometrically it is the opposite, of equal magnitude but in the opposite direction, of its mirror image...
(also called axial vector), the vector potential A is not: A is a polar vector. This means that if the right-hand rule
Right-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
for cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
s were replaced with a left-hand rule, but without changing any other equations or definitions, then B would switch signs, but A would not change. This is an example of a general theorem: The curl of a polar vector is a pseudovector, and vice-versa.
Gauge choices
The above definition does not define the magnetic vector potential uniquely because, by definition, we can arbitrarily add curl-free components to the magnetic potential without changing the observed magnetic field. Thus, there is a degree of freedomDegrees of freedom (physics and chemistry)
A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...
available when choosing A. This condition is known as gauge invariance.
Maxwell's equations in terms of vector potential
Using the above definition of the potentials and applying it to the other two Maxwell's equations (the ones that are not automatically satisfied) results in a complicated differential equation that can be simplified using the Lorenz gauge where A is chosen so as to satisfy:
Using the Lorenz gauge, Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
can be written compactly in terms of the magnetic vector potential A and the electric scalar potential
Electric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
Φ.
In other gauges
Gauge fixing
In the physics of gauge theories, gauge fixing denotes a mathematical procedure for coping with redundant degrees of freedom in field variables. By definition, a gauge theory represents each physically distinct configuration of the system as an equivalence class of detailed local field...
, the equations are different. A different notation to write these same equations (using four-vectors) is shown below.
Calculation of potentials from source distributions
The solutions of Maxwell's equations (in the Lorenz gauge) Feynman and Jackson with the boundary condition that both potentials go to zero sufficiently fast as they approach infinity are called the retarded potentials which are:-
where 
-
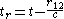
- where
- t is the time at which the value of A and
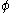are to be calculated. - p1 is the point at which the value of A and
are to be calculated. - p2 is the integration variable.
- r12 is the distance from point p1 to point p2.
- tr is a time earlier than t by
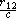which is the time it takes an effect generated at p2 to propagate to p1 at the speed of light. tr is also called retarded time. - A ( p1, t ) is the magnetic vector potential at point p1 and time t.
-
( p1, t )is the electric scalar potential at point p1 and time t. - j ( p1, tr ) is the current density at point p2 and time tr
-
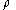( p1, tr ) is the charge density at point p2 and time tr. - V2 is the volume of all points p2 where
or 
is non-zero at least sometimes.
- t is the time at which the value of A and
- where
There are a few notable things about A and
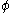calculated in this way:- (The Lorenz gauge conditionLorenz gauge conditionIn electromagnetism, the Lorenz gauge or Lorenz gauge condition is a partial gauge fixing of the electromagnetic vector potential. The condition is that \partial_\mu A^\mu=0...
):
is satisfied. - The position of the source point p2 only enters the equation as a scalar distance from p1 to p2. The direction from p1 to p2 does not enter into the equation. The only thing that matters about a source point is how far away it is.
- The integrand uses retarded time. This simply reflects the fact that changes in the sources propagate at the speed of light
- The equation for A is a vector equation. In Cartesian coordinates, the equation separates into three equations thus:
-
-
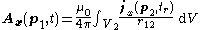where Ax and jx are the components of A and j in the direction of the x axis.
-
- In this form it is easy to see that the component of A in a given direction depends only on the components of
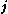that are in the same direction. If the current is carried in a long straight wire, the A points in the same direction as the wire.
In other gauges the formula for A and
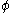is different—for example, see Coulomb gauge for another possibility.Depiction of the A field
See Feynman for the depiction of the A field around a long thin solenoid.Since
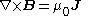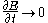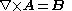(assuming quasi-static conditions, i.e. )and , the lines and contours of A relate to B like the lines and contours of B relate to j. Thus, a depiction of the A field around a loop of B flux (as would be produced in a toroidal inductor) is qualitatively the same as the B field around a loop of current.The figure to the left is an artist's depiction of the A field. The thicker lines indicate paths of higher average intensity (shorter paths have higher intensity so that the path integral is the same). The lines are just drawn to look good and impart general look of the A field.
The drawing tacitly assumes
. This would be true under the following assumptions:- the Coulomb gauge is assumed
- the Lorenz gauge is assumed and there is no distribution of charge,
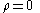
- the Lorenz gauge is assumed and zero frequency is assumed
- the Lorenz gauge is assumed and a non-zero frequency that is low enough to neglect
is assumed
Electromagnetic four-potential
In the context of special relativitySpecial relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
, it is natural to join the magnetic vector potential together with the (scalar) electric potential
Electric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
into the electromagnetic potential, also called "four-potential".
One motivation for doing so is that the four-potential is a mathematical four-vector
Four-vector
In the theory of relativity, a four-vector is a vector in a four-dimensional real vector space, called Minkowski space. It differs from a vector in that it can be transformed by Lorentz transformations. The usage of the four-vector name tacitly assumes that its components refer to a standard basis...
. Thus, using standard four-vector transformation rules, if the electric and magnetic potentials are known in one inertial reference frame, they can be simply calculated in any other inertial reference frame.
Another, related motivation is that the content of classical electromagnetism can be written in a concise and convenient form using the electromagnetic four potential, especially when the Lorenz gauge is used. In particular, in abstract index notation
Abstract index notation
Abstract index notation is a mathematical notation for tensors and spinors that uses indices to indicate their types, rather than their components in a particular basis. The indices are mere placeholders, not related to any fixed basis and, in particular, are non-numerical...
, the set of Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
(in the Lorenz gauge) may be written (in Gaussian units
Gaussian units
Gaussian units comprise a metric system of physical units. This system is the most common of the several electromagnetic unit systems based on cgs units. It is also called the Gaussian unit system, Gaussian-cgs units, or often just cgs units...
) as follows:
where □ is the d'Alembertian and J is the four-current
Four-current
In special and general relativity, the four-current is the Lorentz covariant four-vector that replaces the electromagnetic current density, or indeed any conventional charge current density...
. The first equation is the Lorenz gauge condition
Lorenz gauge condition
In electromagnetism, the Lorenz gauge or Lorenz gauge condition is a partial gauge fixing of the electromagnetic vector potential. The condition is that \partial_\mu A^\mu=0...
while the second contains Maxwell's equations.
Yet another motivation for creating the electromagnetic four-potential is that it plays a very important role in quantum electrodynamics
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
.
Magnetic scalar potential
The magnetic scalar potentialScalar potential
A scalar potential is a fundamental concept in vector analysis and physics . The scalar potential is an example of a scalar field...
is another useful tool in describing the magnetic field, especially for permanent magnets.
In a simply connected domain where there is no free current,
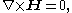
hence we can define magnetic scalar potential ψ as
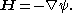
And since
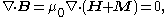
it follows that
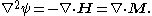
Here
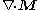acts as the source for magnetic field, much like 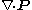as the source for electric field. So analogously to bound electric charge, we can callbound magnetic charge.
If there is free current, one may subtract the contribution of free current per Biot-Savart law
Biot-Savart law
The Biot–Savart law is an equation in electromagnetism that describes the magnetic field B generated by an electric current. The vector field B depends on the magnitude, direction, length, and proximity of the electric current, and also on a fundamental constant called the magnetic constant...
from total magnetic field and solve the remainder with the scalar potential method.