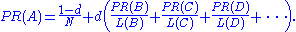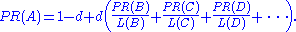PageRank
Encyclopedia
Larry Page
Lawrence "Larry" Page is an American computer scientist and internet entrepreneur who, with Sergey Brin, is best known as the co-founder of Google. As of April 4, 2011, he is also the chief executive of Google, as announced on January 20, 2011...
and used by the Google
Google
Google Inc. is an American multinational public corporation invested in Internet search, cloud computing, and advertising technologies. Google hosts and develops a number of Internet-based services and products, and generates profit primarily from advertising through its AdWords program...
Internet search engine
Search engine
A search engine is an information retrieval system designed to help find information stored on a computer system. The search results are usually presented in a list and are commonly called hits. Search engines help to minimize the time required to find information and the amount of information...
, that assigns a numerical weighting to each element of a hyperlink
Hyperlink
In computing, a hyperlink is a reference to data that the reader can directly follow, or that is followed automatically. A hyperlink points to a whole document or to a specific element within a document. Hypertext is text with hyperlinks...
ed set
Set (computer science)
In computer science, a set is an abstract data structure that can store certain values, without any particular order, and no repeated values. It is a computer implementation of the mathematical concept of a finite set...
of documents, such as the World Wide Web
World Wide Web
The World Wide Web is a system of interlinked hypertext documents accessed via the Internet...
, with the purpose of "measuring" its relative importance within the set. The algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
may be applied to any collection of entities with reciprocal
Reciprocal
-In mathematics:*Multiplicative inverse, in mathematics, the number 1/x, which multiplied by x gives the product 1, also known as a reciprocal*Reciprocal rule, a technique in calculus for calculating derivatives of reciprocal functions...
quotations and references. The numerical weight that it assigns to any given element E is referred to as the PageRank of E and denoted by
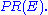
The name "PageRank" is a trademark
Trademark
A trademark, trade mark, or trade-mark is a distinctive sign or indicator used by an individual, business organization, or other legal entity to identify that the products or services to consumers with which the trademark appears originate from a unique source, and to distinguish its products or...
of Google, and the PageRank process has been patent
Patent
A patent is a form of intellectual property. It consists of a set of exclusive rights granted by a sovereign state to an inventor or their assignee for a limited period of time in exchange for the public disclosure of an invention....
ed . However, the patent is assigned to Stanford University
Stanford University
The Leland Stanford Junior University, commonly referred to as Stanford University or Stanford, is a private research university on an campus located near Palo Alto, California. It is situated in the northwestern Santa Clara Valley on the San Francisco Peninsula, approximately northwest of San...
and not to Google. Google has exclusive license rights on the patent from Stanford University. The university received 1.8 million shares of Google in exchange for use of the patent; the shares were sold in 2005 for $
United States dollar
The United States dollar , also referred to as the American dollar, is the official currency of the United States of America. It is divided into 100 smaller units called cents or pennies....
336 million.
Description
A PageRank results from a mathematical algorithm based on the graphGraph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
, the webgraph
Webgraph
The webgraph describes the directed links between pages of the World Wide Web. A graph, in general, consists of several vertices, some pairs connected by edges. In a directed graph, edges are directed lines or arcs...
, created by all World Wide Web pages as nodes and hyperlink
Hyperlink
In computing, a hyperlink is a reference to data that the reader can directly follow, or that is followed automatically. A hyperlink points to a whole document or to a specific element within a document. Hypertext is text with hyperlinks...
s as edges, taking into consideration authority hubs such as cnn.com or usa.gov
USA.gov
USA.gov is the official web portal of the United States government. It is designed to improve the public’s interaction with the U.S. government by quickly directing website visitors to the services or information they are seeking, and by inviting the public to share ideas to improve government...
. The rank value indicates an importance of a particular page. A hyperlink to a page counts as a vote of support. The PageRank of a page is defined recursively
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
and depends on the number and PageRank metric of all pages that link to it ("incoming links"). A page that is linked to by many pages with high PageRank receives a high rank itself. If there are no links to a web page there is no support for that page.
Numerous academic papers concerning PageRank have been published since Page and Brin's original paper. In practice, the PageRank concept has proven to be vulnerable to manipulation, and extensive research has been devoted to identifying falsely inflated PageRank and ways to ignore links from documents with falsely inflated PageRank.
Other link-based ranking algorithms for Web pages include the HITS algorithm
HITS algorithm
Hyperlink-Induced Topic Search is a link analysis algorithm that rates Web pages, developed by Jon Kleinberg. It was a precursor to PageRank...
invented by Jon Kleinberg
Jon Kleinberg
-External links:**** Stephen Ibaraki*Yury Lifshits,...
(used by Teoma
Teoma
Teoma, pronounced chawmuh , was an Internet search engine founded in 2000 by Professor Apostolos Gerasoulis and his colleagues at Rutgers University in New Jersey. Professor Tao Yang from the University of California, Santa Barbara co-led technology R&D. Their research grew out of the 1998 DiscoWeb...
and now Ask.com
Ask.com
Ask is a Q&A focused search engine founded in 1996 by Garrett Gruener and David Warthen in Berkeley, California. The original software was implemented by Gary Chevsky from his own design. Warthen, Chevsky, Justin Grant, and others built the early AskJeeves.com website around that core engine...
), the IBM CLEVER project
CLEVER project
The CLEVER project was a research project in Web search led by Jon Kleinberg at IBM's Almaden Research Center.Techniques developed in CLEVER included various forms of link analysis, including the HITS algorithm....
, and the TrustRank
TrustRank
TrustRank is a link analysis technique described in a paper by Stanford University and Yahoo! researchers for semi-automatically separating useful webpages from spam.Many Web spam pages are created only with the intention of misleading search engines...
algorithm.
History
PageRank was developed at Stanford UniversityStanford University
The Leland Stanford Junior University, commonly referred to as Stanford University or Stanford, is a private research university on an campus located near Palo Alto, California. It is situated in the northwestern Santa Clara Valley on the San Francisco Peninsula, approximately northwest of San...
by Larry Page
Larry Page
Lawrence "Larry" Page is an American computer scientist and internet entrepreneur who, with Sergey Brin, is best known as the co-founder of Google. As of April 4, 2011, he is also the chief executive of Google, as announced on January 20, 2011...
(hence the name Page-Rank) and Sergey Brin
Sergey Brin
Sergey Mikhaylovich Brin is a Russian-born American computer scientist and internet entrepreneur who, with Larry Page, co-founded Google, one of the largest internet companies. , his personal wealth is estimated to be $16.7 billion....
as part of a research project about a new kind of search engine. Sergey Brin had the idea that information on the web could be ordered in a hierarchy by "link popularity": a page is ranked higher as there are more links to it. It was co-authored by Rajeev Motwani
Rajeev Motwani
Rajeev Motwani was a professor of Computer Science at Stanford University whose research focused on theoretical computer science. He was an early advisor and supporter of companies including Google and PayPal, and a special advisor to Sequoia Capital. He was a winner of the Gödel Prize in...
and Terry Winograd
Terry Winograd
Terry Allen Winograd is an American professor of computer science at Stanford University, and co-director of the Stanford Human-Computer Interaction Group...
. The first paper about the project, describing PageRank and the initial prototype of the Google search
Google search
Google or Google Web Search is a web search engine owned by Google Inc. Google Search is the most-used search engine on the World Wide Web, receiving several hundred million queries each day through its various services....
engine, was published in 1998: shortly after, Page and Brin founded Google Inc., the company behind the Google search engine. While just one of many factors that determine the ranking of Google search results, PageRank continues to provide the basis for all of Google's web search tools.
PageRank has been influenced by citation analysis
Citation analysis
Citation analysis is the examination of the frequency, patterns, and graphs of citations in articles and books. It uses citations in scholarly works to establish links to other works or other researchers. Citation analysis is one of the most widely used methods of bibliometrics...
, early developed by Eugene Garfield
Eugene Garfield
Eugene "Gene" Garfield is an American scientist, one of the founders of bibliometrics and scientometrics. He received a PhD in Structural Linguistics from the University of Pennsylvania in 1961. Dr. Garfield was the founder of the Institute for Scientific Information , which was located in...
in the 1950s at the University of Pennsylvania, and by Hyper Search
Hyper Search
Hyper Search has been the first published technique to introduce link analysis for search engines, opening the way for the second-generation of search engines...
, developed by Massimo Marchiori
Massimo Marchiori
Massimo Marchiori is an Italian computer scientist who made major contributions to the development of the World Wide Web.-Biography:...
at the University of Padua. In the same year PageRank was introduced (1998), Jon Kleinberg
Jon Kleinberg
-External links:**** Stephen Ibaraki*Yury Lifshits,...
published his important work on HITS
HITS algorithm
Hyperlink-Induced Topic Search is a link analysis algorithm that rates Web pages, developed by Jon Kleinberg. It was a precursor to PageRank...
. Google's founders cite Garfield, Marchiori, and Kleinberg in their original paper.
A small search engine called "RankDex" from IDD Information Services designed by Robin Li
Robin Li
Robin Li is a Chinese entrepreneur, co-founder of China's most popular search engine Baidu.Li studied information management at Peking University and the State University of New York, Buffalo. In 2000 he founded Baidu with Eric Xu...
was, since 1996, already exploring a similar strategy for site-scoring and page ranking. The technology in RankDex would be patented by 1999 and used later when Li founded Baidu
Baidu
Baidu, Inc. , simply known as Baidu and incorporated on January 18, 2000, is a Chinese web services company headquartered in the Baidu Campus in Haidian District, Beijing, People's Republic of China....
in China. Li's work would be referenced by some of Larry Page's U.S. patents for his Google search methods.
Algorithm
PageRank is a probability distributionProbability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
used to represent the likelihood that a person randomly clicking on links will arrive at any particular page. PageRank can be calculated for collections of documents of any size. It is assumed in several research papers that the distribution is evenly divided among all documents in the collection at the beginning of the computational process. The PageRank computations require several passes, called "iterations", through the collection to adjust approximate PageRank values to more closely reflect the theoretical true value.
A probability is expressed as a numeric value between 0 and 1. A 0.5 probability is commonly expressed as a "50% chance" of something happening. Hence, a PageRank of 0.5 means there is a 50% chance that a person clicking on a random link will be directed to the document with the 0.5 PageRank.
Simplified algorithm
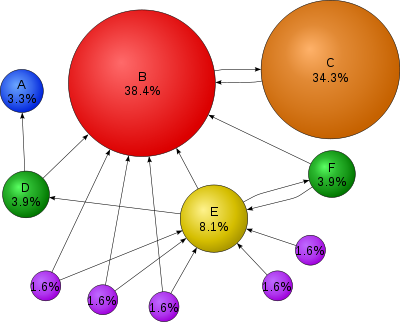
Assume a small universe of four web pages: A, B, C and D. The initial approximation of PageRank would be evenly divided between these four documents. Hence, each document would begin with an estimated PageRank of 0.25.In the original form of PageRank initial values were simply 1. This meant that the sum of all pages was the total number of pages on the web at that time. Later versions of PageRank (see the formulas below) would assume a probability distribution between 0 and 1. Here a simple probability distribution will be used—hence the initial value of 0.25.
If pages B, C, and D each only link to A, they would each confer 0.25 PageRank to A. All PageRank PR in this simplistic system would thus gather to A because all links would be pointing to A.
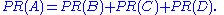
This is 0.75.
Suppose that page B has a link to page C as well as to page A, while page D has links to all three pages. The value of the link-votes is divided among all the outbound links on a page. Thus, page B gives a vote worth 0.125 to page A and a vote worth 0.125 to page C. Only one third of D
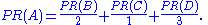
In other words, the PageRank conferred by an outbound link is equal to the document's own PageRank score divided by the normalized number of outbound links L (it is assumed that links to specific URLs only count once per document).
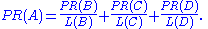
In the general case, the PageRank value for any page u can be expressed as:
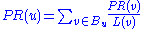 ,
,i.e. the PageRank value for a page u is dependent on the PageRank values for each page v out of the set Bu (this set contains all pages linking to page u), divided by the number L(v) of links from page v.
Damping factor
The PageRank theory holds that even an imaginary surfer who is randomly clicking on links will eventually stop clicking. The probability, at any step, that the person will continue is a damping factor d. Various studies have tested different damping factors, but it is generally assumed that the damping factor will be set around 0.85.The damping factor is subtracted from 1 (and in some variations of the algorithm, the result is divided by the number of documents (N) in the collection) and this term is then added to the product of the damping factor and the sum of the incoming PageRank scores. That is,
So any page's PageRank is derived in large part from the PageRanks of other pages. The damping factor adjusts the derived value downward. The original paper, however, gave the following formula, which has led to some confusion:
The difference between them is that the PageRank values in the first formula sum to one, while in the second formula each PageRank gets multiplied by N and the sum becomes N. A statement in Page and Brin's paper that "the sum of all PageRanks is one" and claims by other Google employees support the first variant of the formula above.
To be more specific, in the latter formula, the probability for the random surfer reaching a page is weighted by the total number of web pages. So, in this version PageRank is an expected value for the random surfer visiting a page, when he restarts this procedure as often as the web has pages. If the web had 100 pages and a page had a PageRank value of 2, the random surfer would reach that page in an average twice if he restarts 100 times. Basically, the two formulas do not differ fundamentally from each other. A PageRank that has been calculated by using the former formula has to be multiplied by the total number of web pages to get the according PageRank that would have been calculated by using the latter formula. Even Page and Brin mixed up the two formulas in their most popular paper "The Anatomy of a Large-Scale Hypertextual Web Search Engine", where they claim the latter formula to form a probability distribution over web pages with the sum of all pages' PageRanks being one.
Google recalculates PageRank scores each time it crawls the Web and rebuilds its index. As Google increases the number of documents in its collection, the initial approximation of PageRank decreases for all documents.
The formula uses a model of a random surfer who gets bored after several clicks and switches to a random page. The PageRank value of a page reflects the chance that the random surfer will land on that page by clicking on a link. It can be understood as a Markov chain
Markov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
in which the states are pages, and the transitions are all equally probable and are the links between pages.
If a page has no links to other pages, it becomes a sink and therefore terminates the random surfing process. If the random surfer arrives at a sink page, it picks another URL
Uniform Resource Locator
In computing, a uniform resource locator or universal resource locator is a specific character string that constitutes a reference to an Internet resource....
at random and continues surfing again.
When calculating PageRank, pages with no outbound links are assumed to link out to all other pages in the collection. Their PageRank scores are therefore divided evenly among all other pages. In other words, to be fair with pages that are not sinks, these random transitions are added to all nodes in the Web, with a residual probability of usually d = 0.85, estimated from the frequency that an average surfer uses his or her browser's bookmark feature.
So, the equation is as follows:

where
 are the pages under consideration,
are the pages under consideration,  is the set of pages that link to
is the set of pages that link to  ,
,  is the number of outbound links on page
is the number of outbound links on page 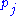 , and N is the total number of pages.
, and N is the total number of pages.The PageRank values are the entries of the dominant eigenvector of the modified adjacency matrix
Adjacency matrix
In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
. This makes PageRank a particularly elegant metric: the eigenvector is
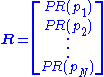
where R is the solution of the equation
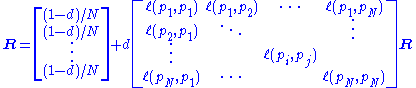
where the adjacency function
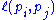 is 0 if page
is 0 if page  does not link to
does not link to  , and normalized such that, for each j
, and normalized such that, for each j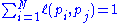 ,
,i.e. the elements of each column sum up to 1, so the matrix is a stochastic matrix
Stochastic matrix
In mathematics, a stochastic matrix is a matrix used to describe the transitions of a Markov chain. It has found use in probability theory, statistics and linear algebra, as well as computer science...
(for more details see the computation section below). Thus this is a variant of the eigenvector centrality measure used commonly in network analysis
Network theory
Network theory is an area of computer science and network science and part of graph theory. It has application in many disciplines including statistical physics, particle physics, computer science, biology, economics, operations research, and sociology...
.
Because of the large eigengap of the modified adjacency matrix above, the values of the PageRank eigenvector are fast to approximate (only a few iterations are needed).
As a result of Markov theory
Markov process
In probability theory and statistics, a Markov process, named after the Russian mathematician Andrey Markov, is a time-varying random phenomenon for which a specific property holds...
, it can be shown that the PageRank of a page is the probability of being at that page after lots of clicks. This happens to equal
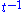 where
where  is the expectation
is the expectationExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of the number of clicks (or random jumps) required to get from the page back to itself.
The main disadvantage is that it favors older pages, because a new page, even a very good one, will not have many links unless it is part of an existing site (a site being a densely connected set of pages, such as Wikipedia
Wikipedia
Wikipedia is a free, web-based, collaborative, multilingual encyclopedia project supported by the non-profit Wikimedia Foundation. Its 20 million articles have been written collaboratively by volunteers around the world. Almost all of its articles can be edited by anyone with access to the site,...
). The Google Directory (itself a derivative of the Open Directory Project
Open Directory Project
The Open Directory Project , also known as Dmoz , is a multilingual open content directory of World Wide Web links. It is owned by Netscape but it is constructed and maintained by a community of volunteer editors.ODP uses a hierarchical ontology scheme for organizing site listings...
) allows users to see results sorted by PageRank within categories. The Google Directory is the only service offered by Google where PageRank directly determines display order. In Google's other search services (such as its primary Web search) PageRank is used to weight the relevance scores of pages shown in search results.
Several strategies have been proposed to accelerate the computation of PageRank.
Various strategies to manipulate PageRank have been employed in concerted efforts to improve search results rankings and monetize advertising links. These strategies have severely impacted the reliability of the PageRank concept, which seeks to determine which documents are actually highly valued by the Web community.
Google is known to penalize link farm
Link farm
On the World Wide Web, a link farm is any group of web sites that all hyperlink to every other site in the group. Although some link farms can be created by hand, most are created through automated programs and services. A link farm is a form of spamming the index of a search engine...
s and other schemes designed to artificially inflate PageRank. In December 2007 Google started actively penalizing sites selling paid text links. How Google identifies link farms and other PageRank manipulation tools are among Google's trade secret
Trade secret
A trade secret is a formula, practice, process, design, instrument, pattern, or compilation of information which is not generally known or reasonably ascertainable, by which a business can obtain an economic advantage over competitors or customers...
s.
Computation
To summarize, PageRank can be either computed iteratively or algebraically. The iterative method can be viewed differently as thepower iteration
Power iteration
In mathematics, the power iteration is an eigenvalue algorithm: given a matrix A, the algorithm will produce a number λ and a nonzero vector v , such that Av = λv....
method, or power method. The basic mathematical operations performed in the iterative method and the power method are identical.
Iterative
In the former case, at , an initial probability distribution is assumed, usually
, an initial probability distribution is assumed, usually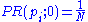 .
.At each time step, the computation, as detailed above, yields
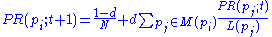 ,
,or in matrix notation
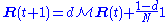 , (*)
, (*)where
 and
and  is the column vector of length
is the column vector of length 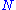 containing only ones.
containing only ones.The matrix
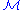 is defined as
is defined as
-

i.e.,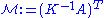 ,
,
where
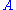 denotes the adjacency matrixAdjacency matrixIn mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
denotes the adjacency matrixAdjacency matrixIn mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
of the graph and is the diagonal matrix with the outdegrees in the diagonal.
is the diagonal matrix with the outdegrees in the diagonal.
The computation ends when for some small
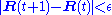 ,
,
i.e., when convergence is assumed.
Algebraic
In the latter case, for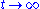 (i.e., in the steady stateSteady stateA system in a steady state has numerous properties that are unchanging in time. This implies that for any property p of the system, the partial derivative with respect to time is zero:...
(i.e., in the steady stateSteady stateA system in a steady state has numerous properties that are unchanging in time. This implies that for any property p of the system, the partial derivative with respect to time is zero:...
), the above equation (*) reads . (**)
. (**)
The solution is given by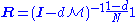 ,
,
with the identity matrixIdentity matrixIn linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
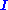 .
.
The solution exists and is unique for . This can be seen by noting that
. This can be seen by noting that  is by construction a stochastic matrixStochastic matrixIn mathematics, a stochastic matrix is a matrix used to describe the transitions of a Markov chain. It has found use in probability theory, statistics and linear algebra, as well as computer science...
is by construction a stochastic matrixStochastic matrixIn mathematics, a stochastic matrix is a matrix used to describe the transitions of a Markov chain. It has found use in probability theory, statistics and linear algebra, as well as computer science...
and hence has an eigenvalue equal to one because of the Perron–Frobenius theoremPerron–Frobenius theoremIn linear algebra, the Perron–Frobenius theorem, proved by and , asserts that a real square matrix with positive entries has a unique largest real eigenvalue and that the corresponding eigenvector has strictly positive components, and also asserts a similar statement for certain classes of...
.
Power Method
If the matrix is a transition probability, i.e., column-stochastic with no columns consisting of
is a transition probability, i.e., column-stochastic with no columns consisting of
just zeros and is a probability distribution (i.e.,
is a probability distribution (i.e.,  ,
,  where
where  is matrix of all ones), Eq. (**) is equivalent to
is matrix of all ones), Eq. (**) is equivalent to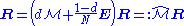 . (***)
. (***)
Hence PageRank is the principal eigenvector of
is the principal eigenvector of  . A fast and easy
. A fast and easy
way to compute this is using the power methodPower iterationIn mathematics, the power iteration is an eigenvalue algorithm: given a matrix A, the algorithm will produce a number λ and a nonzero vector v , such that Av = λv....
: starting with an arbitrary vector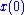 , the operator
, the operator  is applied in succession, i.e.,
is applied in succession, i.e.,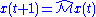 ,
,
until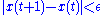 .
.
Note that in Eq. (***) the matrix on the right-hand side in the parenthesis can be interpreted as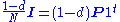 ,
,
where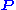 is an initial probability distribution. In the current case
is an initial probability distribution. In the current case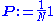 .
.
Finally, if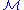 has columns with only zero values, they should be replaced with the initial
has columns with only zero values, they should be replaced with the initial
probability vector
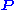 . In other words
. In other words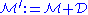 ,
,
where the matrix is defined as
is defined as ,
,
with
In this case, the above two computations using only give the same PageRank if their
only give the same PageRank if their
results are normalized:-
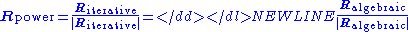 .
.
PageRank matlab/octave implementation
% Parameter M adjacency matrix where Mi,j represents the link from 'j' to 'i', such that for all 'j' sum(i, Mi,j) = 1
% Parameter d damping factor
% Parameter v_quadratic_error quadratic error for v
% Return v vector rank such as vi is the i-th rank from [0, 1]
function [v] = rank(M, d, v_quadratic_error)
N = size(M, 2);
v = rand(N, 1);
v = v ./ norm(v, 2);
last_v = ones(N, 1) * inf;
M_prime = (d .* M) + (((1 - d) / N) .* ones(N, N));
while(norm(v - last_v, 2) > v_quadratic_error)
last_v = v;
v = M_prime * v;
v = v ./ norm(v, 2);
end
Code example for the octave/matlab rank function
M = [0 0 0 0 1 ; 0.5 0 0 0 0 ; 0.5 0 0 0 0 ; 0 1 0.5 0 0 ; 0 0 0.5 1 0];
rank(M, 0.80, 0.001)
Efficiency
Depending on the framework used to perform the computation, the exact implementation of the methods, and the required accuracy of the result, the computation time of the these methods can vary greatly.
Google Toolbar
The Google ToolbarGoogle ToolbarGoogle Toolbar is an Internet browser toolbar only available for Internet Explorer and Firefox .-Google Toolbar 1.0 December 11, 2000:New features:*Direct access to the Google search functionality from any web page*Web Site search...
's PageRank feature displays a visited page's PageRank as a whole number between 0 and 10. The most popular websites have a PageRank of 10. The least have a PageRank of 0. Google has not disclosed the precise method for determining a Toolbar PageRank value. The displayed value is not the actual value Google uses so it is only a rough guide. ‘Toolbar’ PageRank is different from Google PageRank because the PageRank displayed in the toolbar is not 100% reflective of the way Google judges the value of a website.
PageRank measures number of sites which link to particular page. The PageRank of a particular page is roughly based upon the quantity of inbound links as well as the PageRank of the pages providing the links. Other factors are also part of the algorithm such as the size of a page, the number of changes and its up-to-dateness, the key texts in headlines and the words of hyperlinked anchor texts.
The Google Toolbar's PageRank is updated infrequently, so often shows out of date values. The last confirmed update was 27 June 2011, however, there was previously no confirmed update for more than a year.
SERP Rank
The Search engine results pageSearch engine results pageA search engine results page , is the listing of web pages returned by a search engine in response to a keyword query. The results normally include a list of web pages with titles, a link to the page, and a short description showing where the Keywords have matched content within the page...
(SERP) is the actual result returned by a search engine in response to a keyword query. The SERP consists of a list of links to web pages with associated text snippets. The SERP rank of a web page refers to the placement of the corresponding link on the SERP, where higher placement means higher SERP rank. The SERP rank of a web page is not only a function of its PageRank, but depends on a relatively large and continuously adjusted set of factors (over 200), commonly referred to by internet marketers as "Google Love". Search engine optimizationSearch engine optimizationSearch engine optimization is the process of improving the visibility of a website or a web page in search engines via the "natural" or un-paid search results...
(SEO) is aimed at achieving the highest possible SERP rank for a website or a set of web pages.
With the introduction of Google Places into the mainstream organic SERP, PageRank plays little to no role in ranking a business in the Local Business Results. While the theory of citations is still computed in their algorithm, PageRank is not a factor since Google ranks business listings and not web pages.
Google directory PageRank
The Google Directory PageRank is an 8-unit measurement. These values can be viewed in the Google Directory. Unlike the Google Toolbar, which shows the PageRank value by a mouseover of the green bar, the Google Directory does not show the PageRank as a numeric value but only as a green bar.
False or spoofed PageRank
While the PageRank shown in the Toolbar is considered to be derived from an accurate PageRank value (at some time prior to the time of publication by Google) for most sites, this value was at one time easily manipulated. A previous flaw was that any low PageRank page that was redirected, via a HTTP 302HTTP 302The HTTP response status code 302 Found is the most common way of performing a redirection.It is an example of industry practice contradicting the standard HTTP/1.0 specification , which required the client to perform a temporary redirect , but popular browsers implemented it as a 303 See Other , i.e...
response or a "Refresh" meta tag, to a high PageRank page caused the lower PageRank page to acquire the PageRank of the destination page. In theory a new, PR 0 page with no incoming links could have been redirected to the Google home page—which is a PR 10—and then the PR of the new page would be upgraded to a PR10. This spoofingWebsite spoofingWebsite spoofing is the act of creating a website, as a hoax, with the intention of misleading readers that the website has been created by a different person or organisation. Another meaning for spoof is fake websites. Normally, the spoof website will adopt the design of the target website and...
technique, also known as 302 Google JackingPage hijackingPage hijacking is a form of search engine index spamming. It is achieved by creating a rogue copy of a popular website which shows contents similar to the original to a web crawler, but redirects web surfers to unrelated or malicious websites...
, was a known failing or bug in the system. Any page's PageRank could have been spoofed to a higher or lower number of the webmaster's choice and only Google has access to the real PageRank of the page. Spoofing is generally detected by running a Google search for a URL with questionable PageRank, as the results will display the URL of an entirely different site (the one redirected to) in its results.
Manipulating PageRank
For search engine optimizationSearch engine optimizationSearch engine optimization is the process of improving the visibility of a website or a web page in search engines via the "natural" or un-paid search results...
purposes, some companies offer to sell high PageRank links to webmasters. As links from higher-PR pages are believed to be more valuable, they tend to be more expensive. It can be an effective and viable marketing strategy to buy link advertisements on content pages of quality and relevant sites to drive traffic and increase a webmaster's link popularity. However, Google has publicly warned webmasters that if they are or were discovered to be selling links for the purpose of conferring PageRank and reputation, their links will be devalued (ignored in the calculation of other pages' PageRanks). The practice of buying and selling links is intensely debated across the Webmaster community. Google advises webmasters to use the nofollowNofollownofollow is a value that can be assigned to the rel attribute of an HTML a element to instruct some search engines that a hyperlink should not influence the link target's ranking in the search engine's index...
HTMLHTMLHyperText Markup Language is the predominant markup language for web pages. HTML elements are the basic building-blocks of webpages....
attributeAttribute (computing)In computing, an attribute is a specification that defines a property of an object, element, or file. It may also refer to or set the specific value for a given instance of such....
value on sponsored links. According to Matt CuttsMatt CuttsMatt Cutts works for the Search Quality group in Google, specializing in search engine optimization issues. In an interview with USA Today in June 2008, Cutts provided advice on how to optimize search results on Google.-Career:...
, Google is concerned about webmasters who try to game the system, and thereby reduce the quality and relevancy of Google search results.
The intentional surfer model
The original PageRank algorithm reflects the so-called random surfer model, meaning that the PageRank of a particular page is derived from the theoretical probability of visiting that page when clicking on links at random. However, real users do not randomly surf the web, but follow links according to their interest and intention. A page ranking model that reflects the importance of a particular page as a function of how many actual visits it receives by real users is called the intentional surfer model. The Google toolbar sends information to Google for every page visited, and thereby provides a basis for computing PageRank based on the intentional surfer model. The introduction of the nofollowNofollownofollow is a value that can be assigned to the rel attribute of an HTML a element to instruct some search engines that a hyperlink should not influence the link target's ranking in the search engine's index...
attribute by Google to combat SpamdexingSpamdexingIn computing, spamdexing is the deliberate manipulation of search engine indexes...
has the side effect that webmasters commonly use it on outgoing links to increase their own PageRank. This causes a loss of actual links for the Web crawlers to follow, thereby making the original PageRank algorithm based on the random surfer model potentially unreliable. Using information about users' browsing habits provided by the Google toolbar partly compensates for the loss of information caused by the nofollowNofollownofollow is a value that can be assigned to the rel attribute of an HTML a element to instruct some search engines that a hyperlink should not influence the link target's ranking in the search engine's index...
attribute. The SERPSearch engine results pageA search engine results page , is the listing of web pages returned by a search engine in response to a keyword query. The results normally include a list of web pages with titles, a link to the page, and a short description showing where the Keywords have matched content within the page...
rank of a page, which determines a page's actual placement in the search results, is based on a combination of the random surfer model (PageRank) and the intentional surfer model (browsing habits) in addition to other factors.
Other uses
A version of PageRank has recently been proposed as a replacement for the traditional Institute for Scientific InformationInstitute for Scientific InformationThe Institute for Scientific Information was founded by Eugene Garfield in 1960. It was acquired by Thomson Scientific & Healthcare in 1992, became known as Thomson ISI and now is part of the Healthcare & Science business of the multi-billion dollar Thomson Reuters Corporation.ISI offered...
(ISI) impact factorImpact factorThe impact factor, often abbreviated IF, is a measure reflecting the average number of citations to articles published in science and social science journals. It is frequently used as a proxy for the relative importance of a journal within its field, with journals with higher impact factors deemed...
, and implemented at eigenfactor.org. Instead of merely counting total citation to a journal, the "importance" of each citation is determined in a PageRank fashion.
A similar new use of PageRank is to rank academic doctoral programs based on their records of placing their graduates in faculty positions. In PageRank terms, academic departments link to each other by hiring their faculty from each other (and from themselves).
PageRank has been used to rank spaces or streets to predict how many people (pedestrians or vehicles) come to the individual spaces or streets. In lexical semanticsLexical semanticsLexical semantics is a subfield of linguistic semantics. It is the study of how and what the words of a language denote . Words may either be taken to denote things in the world, or concepts, depending on the particular approach to lexical semantics.The units of meaning in lexical semantics are...
it has been used to perform Word Sense DisambiguationWord sense disambiguationIn computational linguistics, word-sense disambiguation is an open problem of natural language processing, which governs the process of identifying which sense of a word is used in a sentence, when the word has multiple meanings...
and to automatically rank WordNetWordNetWordNet is a lexical database for the English language. It groups English words into sets of synonyms called synsets, provides short, general definitions, and records the various semantic relations between these synonym sets...
synsets according to how strongly they possess a given semantic property, such as positivity or negativity.
A dynamic weighting method similar to PageRank has been used to generate customized reading lists based on the link structure of Wikipedia.
A Web crawlerWeb crawlerA Web crawler is a computer program that browses the World Wide Web in a methodical, automated manner or in an orderly fashion. Other terms for Web crawlers are ants, automatic indexers, bots, Web spiders, Web robots, or—especially in the FOAF community—Web scutters.This process is called Web...
may use PageRank as one of a number of importance metrics it uses to determine which URL to visit during a crawl of the web. One of the early working papers
that were used in the creation of Google is Efficient crawling through URL ordering,
which discusses the use of a number of different importance metrics to determine how deeply, and how much of a site Google will crawl. PageRank is presented as one of a number of these importance metrics, though there are others listed such as the number of inbound and outbound links for a URL, and the distance from the root directory on a site to the URL.
The PageRank may also be used as a methodology to measure the apparent impact of a community like the BlogosphereBlogosphereThe blogosphere is made up of all blogs and their interconnections. The term implies that blogs exist together as a connected community or as a social network in which everyday authors can publish their opinions...
on the overall Web itself. This approach uses therefore the PageRank to measure the distribution of attention in reflection of the Scale-free networkScale-free networkA scale-free network is a network whose degree distribution follows a power law, at least asymptotically. That is, the fraction P of nodes in the network having k connections to other nodes goes for large values of k as...
paradigm.
In any ecosystem, a modified version of PageRank may be used to determine species that are essential to the continuing health of the environment.
An application of PageRank to the analysis of protein networks in biology is reported recently.
nofollow
In early 2005, Google implemented a new value, "nofollowNofollownofollow is a value that can be assigned to the rel attribute of an HTML a element to instruct some search engines that a hyperlink should not influence the link target's ranking in the search engine's index...
", for the rel attribute of HTML link and anchor elements, so that website developers and blogBlogA blog is a type of website or part of a website supposed to be updated with new content from time to time. Blogs are usually maintained by an individual with regular entries of commentary, descriptions of events, or other material such as graphics or video. Entries are commonly displayed in...
gers can make links that Google will not consider for the purposes of PageRank—they are links that no longer constitute a "vote" in the PageRank system. The nofollow relationship was added in an attempt to help combat spamdexingSpamdexingIn computing, spamdexing is the deliberate manipulation of search engine indexes...
.
As an example, people could previously create many message-board posts with links to their website to artificially inflate their PageRank. With the nofollow value, message-board administrators can modify their code to automatically insert "rel='nofollow'" to all hyperlinks in posts, thus preventing PageRank from being affected by those particular posts. This method of avoidance, however, also has various drawbacks, such as reducing the link value of legitimate comments. (See: Spam in blogs#nofollow)
In an effort to manually control the flow of PageRank among pages within a website, many webmasters practice what is known as PageRank Sculpting—which is the act of strategically placing the nofollow attribute on certain internal links of a website in order to funnel PageRank towards those pages the webmaster deemed most important. This tactic has been used since the inception of the nofollow attribute, but may no longer be effective since Google announced that blocking PageRank transfer with nofollow does not redirect that PageRank to other links.
Deprecation
PageRank was once available for the verified site maintainers through the Google Webmaster Tools interface. However on October 15, 2009, a Google employee confirmed that the company had removed PageRank from its Webmaster Tools section, explaining that "We’ve been telling people for a long time that they shouldn’t focus on PageRank so much; many site owners seem to think it's the most important metric for them to track, which is simply not true." The PageRank indicator is not available in Google's own ChromeGoogle ChromeGoogle Chrome is a web browser developed by Google that uses the WebKit layout engine. It was first released as a beta version for Microsoft Windows on September 2, 2008, and the public stable release was on December 11, 2008. The name is derived from the graphical user interface frame, or...
browser.
The visible page rank is updated very infrequently. After the rank in the Google toolbar was updated in 3 April 2010, there was no confirmed update for more than 9 months, while it was finally updated afterwards. Some authors ask not when but rather if the rank will be updated again.
Google may be moving away from a publicly visible page rank in order to motivate work on content quality by discouraging content farmContent farmIn the context of the World Wide Web, the term content farm is used to describe a company that employs large numbers of often freelance writers to generate large amounts of textual content which is specifically designed to satisfy algorithms for maximal retrieval by automated search engines...
ing as a means of boosting a site's reputation. A visible, high rank can inflate the value of a site, and provides useful feedback for paid SEOsSearch engine optimizationSearch engine optimization is the process of improving the visibility of a website or a web page in search engines via the "natural" or un-paid search results...
that add no value to the system. In addition, Google has been criticized and even sued for perceived low ranks.
On , many users mistakenly thought Google PageRank was gone. As it turns out, it was simply an update to the URL used to query the PageRank from Google.
See also
- EigenTrustEigenTrustEigenTrust algorithm is a reputation management algorithm for peer-to-peer networks, developed by Sep Kamvar, Mario Schlosser, and Hector Garcia-Molina...
— a decentralized PageRank algorithm - Google bombGoogle bombThe terms Google bomb and Googlewashing refer to practices, such as creating large numbers of links, that cause a web page to have a high ranking for searches on unrelated or off topic keyword phrases, often for comical or satirical purposes...
- Google searchGoogle searchGoogle or Google Web Search is a web search engine owned by Google Inc. Google Search is the most-used search engine on the World Wide Web, receiving several hundred million queries each day through its various services....
- Google matrixGoogle matrixA Google matrix is a particular stochastic matrix that is used by Google's PageRank algorithm. The matrix represents a graph with edges representing links between pages....
- Google PandaGoogle PandaGoogle Panda is a change to the Google's search results ranking algorithm that was first released in February 2011 . The change aimed to lower the rank of "low-quality sites", and return higher-quality sites near the top of the search results...
- Hilltop algorithmHilltop algorithmThe Hilltop algorithm is an algorithm used to find documents relevant to a particular keyword topic. Created by Krishna Bharat while he was at Compaq Systems Research Center and George A. Mihăilă, then at the University of Toronto, it was acquired by Google in February 2003...
- Link love
- Methods of website linkingMethods of website linkingThis article pertains to methods of hyperlinking to/of different websites, often used in regard to search engine optimization . Many techniques and special terminology about linking are described below.-Reciprocal link:...
- PigeonRank
- Power method — the iterative eigenvector algorithm used to calculate PageRank
- Search engine optimizationSearch engine optimizationSearch engine optimization is the process of improving the visibility of a website or a web page in search engines via the "natural" or un-paid search results...
- SimRankSimRankSimRank is a general similarity measure, based on a simple and intuitive graph-theoretic model.SimRank is applicable in any domain with object-to-object relationships, that measures similarity of the structural context in which objects occur, based on their relationships with other...
— a measure of object-to-object similarity based on random-surfer model - Topic-Sensitive PageRank
- TrustRankTrustRankTrustRank is a link analysis technique described in a paper by Stanford University and Yahoo! researchers for semi-automatically separating useful webpages from spam.Many Web spam pages are created only with the intention of misleading search engines...
- WebgraphWebgraphThe webgraph describes the directed links between pages of the World Wide Web. A graph, in general, consists of several vertices, some pairs connected by edges. In a directed graph, edges are directed lines or arcs...
- CheiRankCheiRankThe CheiRank is an eigenvector with a maximal real eigenvalue of the Google matrix G^* constructed for a directed network with the inverted directions of links. It is similar to the PageRank vector, which ranks the network nodes in average proportionally to a number of incoming links being the...
Relevant patents
- Original PageRank U.S. Patent—Method for node ranking in a linked database—Patent number 6,285,999—September 4, 2001
- PageRank U.S. Patent—Method for scoring documents in a linked database—Patent number 6,799,176—September 28, 2004
- PageRank U.S. Patent—Method for node ranking in a linked database—Patent number 7,058,628—June 6, 2006
- PageRank U.S. Patent—Scoring documents in a linked database—Patent number 7,269,587—September 11, 2007
External links
- Our Search: Google Technology by Google
- How Google Finds Your Needle in the Web's Haystack by the American Mathematical Society
- Web PageRank prediction with Markov models Michalis Vazirgiannis, Dimitris Drosos, Pierre Senellart, Akrivi Vlachou - Research paper
- Scientist discovers PageRank-type algorithm from the 1940s—February 17, 2010
- EigenTrust
-