Rydberg formula
Encyclopedia
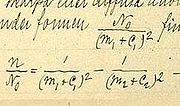
Atomic physics
Atomic physics is the field of physics that studies atoms as an isolated system of electrons and an atomic nucleus. It is primarily concerned with the arrangement of electrons around the nucleus and...
to describe the wavelengths of spectral lines of many chemical element
Chemical element
A chemical element is a pure chemical substance consisting of one type of atom distinguished by its atomic number, which is the number of protons in its nucleus. Familiar examples of elements include carbon, oxygen, aluminum, iron, copper, gold, mercury, and lead.As of November 2011, 118 elements...
s. It was formulated by the Swedish physicist
Physicist
A physicist is a scientist who studies or practices physics. Physicists study a wide range of physical phenomena in many branches of physics spanning all length scales: from sub-atomic particles of which all ordinary matter is made to the behavior of the material Universe as a whole...
Johannes Rydberg
Johannes Rydberg
Johannes Robert Rydberg, , , was a Swedish physicist mainly known for devising the Rydberg formula, in 1888, which is used to predict the wavelengths of photons emitted by changes in the energy level of an electron in a hydrogen atom.The physical constant known as the...
, and presented on November 5, 1888.
History
In the 1880s, Rydberg worked on a formula describing the relation between the wavelengths in spectral lines of alkali metals. He noticed that lines came in series and he found that he could simplify his calculations by using the wavenumberWavenumber
In the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
(the number of waves occupying a set unit of length, equal to 1/λ, the inverse of the wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
) as his unit of measurement. He plotted the wavenumbers (n) of successive lines in each series against consecutive integers which represented the order of the lines in that particular series. Finding that the resulting curves were similarly shaped, he sought a single function which could generate all of them, when appropriate constants were inserted.
First he tried the formula:
, where n is the line's wavenumber, n0 is the series limit, m is the line's ordinal number in the series, m is a constant different for different series and C0 is a universal constant. This did not work very well.Rydberg was trying:
when he became aware of Balmer's formula for the hydrogen spectrum 
In this equation, m is an integer and h is a constant (not to be confused with the later Planck's constant, a completely different number now usually given the symbol h).Rydberg therefore rewrote Balmer's formula in terms of wavenumbers, as
.This suggested that the Balmer formula for hydrogen might be a special case with
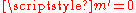and 
, where 
, the reciprocal of Balmer's constant (this constant h is written B in the Balmer equation article, again to avoid confusion with Planck's constant).The term Co was found to be a universal constant common to all elements, equal to 4/h. This constant is now known as the Rydberg constant
Rydberg constant
The Rydberg constant, symbol R∞, named after the Swedish physicist Johannes Rydberg, is a physical constant relating to atomic spectra in the science of spectroscopy. Rydberg initially determined its value empirically from spectroscopy, but Niels Bohr later showed that its value could be calculated...
, and m is known as the quantum defect
Quantum defect
The term quantum defect is ambiguous. Various meanings are discussed below. Characteristic is that the defect deals with the loss on the smallest energy scale of light: that of the quantum.-Quantum defect in laser science:...
.
As stressed by Niels Bohr
Niels Bohr
Niels Henrik David Bohr was a Danish physicist who made foundational contributions to understanding atomic structure and quantum mechanics, for which he received the Nobel Prize in Physics in 1922. Bohr mentored and collaborated with many of the top physicists of the century at his institute in...
, expressing results in terms of wavenumber, not wavelength, was the key to Rydberg's discovery. The fundamental role of wavenumbers was also emphasized by the Rydberg-Ritz combination principle
Rydberg-Ritz combination principle
The Rydberg-Ritz Combination Principle is the theory proposed by Walter Ritz in 1908 to explain relationship of the spectral lines for all atoms...
of 1908. The fundamental reason for this lies in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. Light's wavenumber is proportional to frequency
, and therefore also proportional to light's quantum energy E. Thus, 
. Modern understanding is that Rydberg's findings were a reflection of the underlying simplicity of the behavior of spectral lines, in terms of fixed (quantized) energy differences between electronElectron
The electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
orbitals in atoms. Rydberg's 1888 classical expression for the form of the spectral series was not accompanied by a physical explanation. Ritz's pre-quantum 1908 explanation for the mechanism underlying the spectral series was that atomic electrons behaved like magnets and that the magnets could vibrate with respect to the atomic nucleus (at least temporarily) to produce electromagnetic radiation, but this theory was superseded in 1913 by Niels Bohr
Niels Bohr
Niels Henrik David Bohr was a Danish physicist who made foundational contributions to understanding atomic structure and quantum mechanics, for which he received the Nobel Prize in Physics in 1922. Bohr mentored and collaborated with many of the top physicists of the century at his institute in...
's model of the atom
Bohr model
In atomic physics, the Bohr model, introduced by Niels Bohr in 1913, depicts the atom as a small, positively charged nucleus surrounded by electrons that travel in circular orbits around the nucleus—similar in structure to the solar system, but with electrostatic forces providing attraction,...
.
In Bohr's conception of the atom, the integer Rydberg (and Balmer) n numbers represent electron orbitals at different integral distances from the atom. A frequency (or spectral energy) emitted in a transition from n1 to n2 therefore represents the photon energy emitted or absorbed when an electron makes a jump from orbital 1 to orbital 2.
Rydberg formula for hydrogen
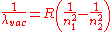
Where
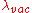is the wavelengthWavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
of electromagnetic radiation emitted in vacuum
Vacuum
In everyday usage, vacuum is a volume of space that is essentially empty of matter, such that its gaseous pressure is much less than atmospheric pressure. The word comes from the Latin term for "empty". A perfect vacuum would be one with no particles in it at all, which is impossible to achieve in...
,
is the Rydberg constantRydberg constant
The Rydberg constant, symbol R∞, named after the Swedish physicist Johannes Rydberg, is a physical constant relating to atomic spectra in the science of spectroscopy. Rydberg initially determined its value empirically from spectroscopy, but Niels Bohr later showed that its value could be calculated...
, approximately 1.097 * 107 m-1,
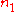and 
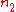are integers such that 
.By setting
to 1 and letting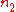 
run from 2 to infinity, the spectral lines known as the Lyman seriesLyman series
In physics and chemistry, the Lyman series is the series of transitions and resulting ultraviolet emission lines of the hydrogen atom as an electron goes from n ≥ 2 to n = 1...
converging to 91 nm are obtained, in the same manner:
| n1 | n2 | Name | Converge toward |
|---|---|---|---|
| 1 | 2 → ∞ | Lyman series Lyman series In physics and chemistry, the Lyman series is the series of transitions and resulting ultraviolet emission lines of the hydrogen atom as an electron goes from n ≥ 2 to n = 1... |
91.13 nm (UV Ultraviolet Ultraviolet light is electromagnetic radiation with a wavelength shorter than that of visible light, but longer than X-rays, in the range 10 nm to 400 nm, and energies from 3 eV to 124 eV... ) |
| 2 | 3 → ∞ | Balmer series Balmer series The Balmer series or Balmer lines in atomic physics, is the designation of one of a set of six different named series describing the spectral line emissions of the hydrogen atom.... |
364.51 nm (Visible Visible spectrum The visible spectrum is the portion of the electromagnetic spectrum that is visible to the human eye. Electromagnetic radiation in this range of wavelengths is called visible light or simply light. A typical human eye will respond to wavelengths from about 390 to 750 nm. In terms of... ) |
| 3 | 4 → ∞ | Paschen series | 820.14 nm (IR Infrared Infrared light is electromagnetic radiation with a wavelength longer than that of visible light, measured from the nominal edge of visible red light at 0.74 micrometres , and extending conventionally to 300 µm... ) |
| 4 | 5 → ∞ | Brackett series | 1458.03 nm (Far IR) |
| 5 | 6 → ∞ | Pfund series | 2278.17 nm (Far IR) |
| 6 | 7 → ∞ | Humphreys series | 3280.56 nm (Far IR) |
Rydberg formula for any hydrogen-like element
The formula above can be extended for use with any hydrogen-likeHydrogen-like atom
A hydrogen-like ion is any atomic nucleus with one electron and thus is isoelectronic with hydrogen. Except for the hydrogen atom itself , these ions carry the positive charge e, where Z is the atomic number of the atom. Examples of hydrogen-like ions are He+, Li2+, Be3+ and B4+...
chemical element
Chemical element
A chemical element is a pure chemical substance consisting of one type of atom distinguished by its atomic number, which is the number of protons in its nucleus. Familiar examples of elements include carbon, oxygen, aluminum, iron, copper, gold, mercury, and lead.As of November 2011, 118 elements...
s with
where
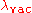is the wavelengthWavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
of the light emitted in vacuum
Vacuum
In everyday usage, vacuum is a volume of space that is essentially empty of matter, such that its gaseous pressure is much less than atmospheric pressure. The word comes from the Latin term for "empty". A perfect vacuum would be one with no particles in it at all, which is impossible to achieve in...
;
is the Rydberg constantRydberg constant
The Rydberg constant, symbol R∞, named after the Swedish physicist Johannes Rydberg, is a physical constant relating to atomic spectra in the science of spectroscopy. Rydberg initially determined its value empirically from spectroscopy, but Niels Bohr later showed that its value could be calculated...
for this element;
is the atomic numberAtomic number
In chemistry and physics, the atomic number is the number of protons found in the nucleus of an atom and therefore identical to the charge number of the nucleus. It is conventionally represented by the symbol Z. The atomic number uniquely identifies a chemical element...
, i.e. the number of proton
Proton
The proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....
s in the atomic nucleus
Atomic nucleus
The nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...
of this element;
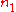and 
are integers such that 
.It's important to notice that this formula can be directly applied only to hydrogen-like, also called hydrogenic atoms of chemical element
Chemical element
A chemical element is a pure chemical substance consisting of one type of atom distinguished by its atomic number, which is the number of protons in its nucleus. Familiar examples of elements include carbon, oxygen, aluminum, iron, copper, gold, mercury, and lead.As of November 2011, 118 elements...
s, i.e. atoms with only one electron being affected by an effective nuclear charge (which is easily estimated). Examples would include He+, Li2+, Be3+ etc., where no other electrons exist in the atom.
But the Rydberg formula also provides correct wavelengths for distant electrons, where the effective nuclear charge can be estimated as the same as that for hydrogen, since all but one of the nuclear charges have been screened by other electrons, and the core of the atom has an effective positive charge of +1.
Finally, with certain modifications (replacement of Z by Z−1, and use of the integers 1 and 2 for the ns to give a numerical value of for the difference of their inverse squares), the Rydberg formula provides correct values in the special case of K-alpha
K-alpha
In X-ray spectroscopy, K-alpha emission lines result when an electron transitions to the innermost "K" shell from a 2p orbital of the second or "L" shell...
lines, since the transition in question is the K-alpha transition of the electron from the 1s orbital to the 2p orbital. This is analogous to the Lyman-alpha line
Lyman-alpha line
In physics, the Lyman-alpha line, sometimes written as Ly-\alpha line, is a spectral line of hydrogen, or more generally of one-electron ions, in the Lyman series, emitted when the electron falls from the n = 2 orbital to the n = 1 orbital, where n is the principal quantum number...
transition for hydrogen, and has the same frequency factor. Because the 2p electron is not screened by any other electrons in the atom from the nucleus, the nuclear charge is diminished only by the single remaining 1s electron, causing the system to be effectively a hydrogenic atom, but with a diminished nuclear charge Z−1. Its frequency is thus the Lyman-alpha hydrogen frequency, increased by a factor of (Z−1)2. This formula of f = c/λ = (Lyman-alpha frequency)⋅(Z−1)2 is historically known as Moseley's law
Moseley's law
Moseley's law is an empirical law concerning the characteristic x-rays that are emitted by atoms. The law was discovered and published by the English physicist Henry Moseley in 1913...
(having added a factor c to convert wavelength to frequency), and can be used to predict wavelengths of the Kα (K-alpha) X-ray spectral emission lines of chemical elements from aluminum to gold. See the biography of Henry Moseley
Henry Moseley
Henry Gwyn Jeffreys Moseley was an English physicist. Moseley's outstanding contribution to the science of physics was the justification from physical laws of the previous empirical and chemical concept of the atomic number. This stemmed from his development of Moseley's law in X-ray spectra...
for the historical importance of this law, which was derived empirically at about the same time it was explained by the Bohr model
Bohr model
In atomic physics, the Bohr model, introduced by Niels Bohr in 1913, depicts the atom as a small, positively charged nucleus surrounded by electrons that travel in circular orbits around the nucleus—similar in structure to the solar system, but with electrostatic forces providing attraction,...
of the atom.
For other spectral transitions in multi-electron atoms, the Rydberg formula generally provides incorrect results, since the magnitude of the screening of inner electrons for outer-electron transitions is variable and not possible to compensate for in the simple manner above.