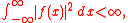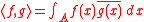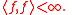In mathematics, a quadratically integrable function, also called a square-integrable function, is a real

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

- or complex

Complex number

A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...

-valued measurable function

Measurable function

In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...

 for which the integral

Integral

Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...

 of the square of the absolute value

Absolute value

In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...

 is finite. Thus, if

then ƒ is quadratically integrable on the real line (−∞, ∞). One may also speak of quadratic integrability over bounded intervals such as [0, 1].

The quadratically integrable functions form an inner product space

Inner product space

In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...

 whose inner product is given by

where
is the complex conjugate

Complex conjugate

In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...

 of g,

• A is the set over which one integrates—in the first example above, A is (−∞, ∞); in the second, A is [0, 1].

Since |a|² = a , quadratic integrability is the same as saying

It can be shown that quadratically integrable functions form a complete metric space, hence a Banach space

Banach space

In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...

. As we have the additional property of the inner product, this is specifically a Hilbert space

Hilbert space

The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...

. This inner product space is conventionally denoted L².

The space of quadratically integrable functions is the L^p space

Lp space

In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...

in which p = 2.