
Orientation (geometry)
Encyclopedia
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
the orientation, angular position, or attitude of an object such as a line
Line (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
, plane or rigid body
Rigid body
In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...
is part of the description of how it is placed in the space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
it is in.
Namely, it is the imaginary rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
that is needed to move the object from a reference placement to its current placement. A rotation may not be enough to reach the current placement. It may be necessary to add an imaginary translation
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
, called the object's location (or position, or linear position). The location and orientation together fully describe how the object is placed in space. The above mentioned imaginary rotation and translation may be thought to occur in any order, as the orientation of an object does not change when it translates, and its location does not change when it rotates.
Euler's rotation theorem
Euler's rotation theorem
In geometry, Euler's rotation theorem states that, in three-dimensional space, any displacement of a rigid body such that a point on the rigid body remains fixed, is equivalent to a single rotation about some axis that runs through the fixed point. It also means that the composition of two...
shows that any orientation can be reached with a single rotation around a fixed axis
Rotation around a fixed axis
Rotation around a fixed axis is a special case of rotational motion. The fixed axis hypothesis exclude the possibility of a moving axis, and cannot describe such phenomena as wobbling or precession. According to Euler's rotation theorem, simultaneous rotation around more than one axis at the same...
. This gives one common way of representing the orientation using an axis-angle representation. Other widely used methods include rotation quaternions
Quaternions and spatial rotation
Unit quaternions provide a convenient mathematical notation for representing orientations and rotations of objects in three dimensions. Compared to Euler angles they are simpler to compose and avoid the problem of gimbal lock. Compared to rotation matrices they are more numerically stable and may...
, Euler angles
Euler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...
, or rotation matrices. More specialist uses include Miller indices in crystallography, strike and dip
Strike and dip
Strike and dip refer to the orientation or attitude of a geologic feature. The strike line of a bed, fault, or other planar feature is a line representing the intersection of that feature with a horizontal plane. On a geologic map, this is represented with a short straight line segment oriented...
in geology and grade on maps and signs.
Typically, the orientation is given relative to a frame of reference
Frame of reference
A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...
, usually specified by a Cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
.
Three dimensions
In general the position and orientation in space of a rigid bodyRigid body
In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...
are defined as the position and orientation, relative to the main reference frame, of another reference frame, which is fixed relative to the body, and hence translates and rotates with it (the body's local reference frame, or local coordinate system). At least three independent values are needed to describe the orientation of this local frame. Three other values are needed to describe its location. Thus, a rigid body free to move in space is said to have six degrees of freedom.
All the points of the body change their position during a rotation except for those lying on the rotation axis. If the rigid body has rotational symmetry
Rotational symmetry
Generally speaking, an object with rotational symmetry is an object that looks the same after a certain amount of rotation. An object may have more than one rotational symmetry; for instance, if reflections or turning it over are not counted, the triskelion appearing on the Isle of Man's flag has...
not all orientations are distinguishable, except by observing how the orientation evolves in time from a known starting orientation. For example, the orientation in space of a line
Line (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
, line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
, or vector can be specified with only two values, for example two direction cosines. Another example is the position of a point on the earth, often described using the orientation of a line joining it with the earth center, measured using the two angles of longitude and latitude. Likewise, the orientation of a plane can be described with two values as well, for instance by specifying the orientation of a line normal
Surface normal
A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...
to that plane, or by using the strike and dip angles.
Further details about the mathematical methods to represent the orientation of rigid bodies and planes in three dimensions are given in the following sections.
Two dimensions
In two dimensions the orientation of any object (line, vector, or plane figure) is given by a single value: the angle through which it has rotated. There is only one degree of freedom and only one fixed point about which the rotation takes place.Rigid body in three dimensions
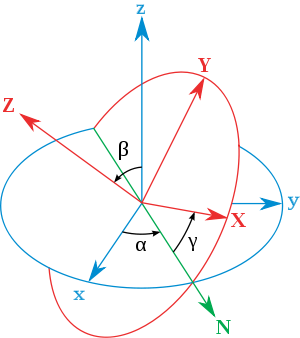
Several methods to describe orientations of a rigid body in three dimensions have been developed. They are summarized in the following sections.Euler angles
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
. He imagined three reference frames that could rotate one around the other, and realized that by starting with a fixed reference frame and performing three rotations, he could get any other reference frame in the space (using two rotations to fix the vertical axis and other to fix the other two axes). The values of these three rotations are called Euler angles
Euler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...
.
Tait-Bryan angles
These are three angles, also known as yaw, pitch and roll, Navigation angles and Cardan angles. Mathematically they constitute a set of six possibilities inside the twelve possible sets of Euler angles, the ordering being the one best used for describing the orientation of a vehicle such as an airplane. In aerospace engineering they are usually referred to as Euler angles.Orientation vector
Euler also realized that the composition of two rotations is equivalent to a single rotation about a different fixed axis (Euler's rotation theoremEuler's rotation theorem
In geometry, Euler's rotation theorem states that, in three-dimensional space, any displacement of a rigid body such that a point on the rigid body remains fixed, is equivalent to a single rotation about some axis that runs through the fixed point. It also means that the composition of two...
). Therefore the composition of the former three angles has to be equal to only one rotation, whose axis was complicated to calculate until matrices were developed.
Based on this fact he introduced a vectorial way to describe any rotation, with a vector on the rotation axis and module equal to the value of the angle. Therefore any orientation can be represented by a rotation vector (also called Euler vector) that leads to it from the reference frame. When used to represent an orientation, the rotation vector is commonly called orientation vector, or attitude vector.
A similar method, called axis-angle representation, describes a rotation or orientation using a unit vector aligned with the rotation axis, and a separate value to indicate the angle (see figure).
Orientation matrix
With the introduction of matrices the Euler theorems were rewritten. The rotations were described by orthogonal matricesOrthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
referred to as rotation matrices or direction cosine matrices. When used to represent an orientation, a rotation matrix is commonly called orientation matrix, or attitude matrix.
The above mentioned Euler vector is the eigenvector of a rotation matrix (a rotation matrix has a unique real eigenvalue).
The product of two rotation matrices is the composition of rotations. Therefore, as before, the orientation can be given as the rotation from the initial frame to achieve the frame that we want to describe.
The configuration space
Configuration space
- Configuration space in physics :In classical mechanics, the configuration space is the space of possible positions that a physical system may attain, possibly subject to external constraints...
of a non-symmetrical
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
object in n-dimensional space is SO(n)
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
×
Product topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
Rn
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. Orientation may be visualized by attaching a basis of tangent vectors
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
to an object. The direction in which each vector points determines its orientation.
Orientation quaternion
Another way to describe rotations is using rotation quaternionsQuaternions and spatial rotation
Unit quaternions provide a convenient mathematical notation for representing orientations and rotations of objects in three dimensions. Compared to Euler angles they are simpler to compose and avoid the problem of gimbal lock. Compared to rotation matrices they are more numerically stable and may...
, also called versors. They are equivalent to rotation matrices and rotation vectors. With respect to rotation vectors, they can be more easily converted to and from matrices. When used to represent orientations, rotation quaternions are typically called orientation quaternions or attitude quaternions.
Miller indices
The attitude of a lattice planeLattice plane
In crystallography, a lattice plane of a given Bravais lattice is a plane whose intersections with the lattice are periodic and intersect the Bravais lattice; equivalently, a lattice plane is any plane containing at least three noncollinear Bravais lattice points...
is the orientation of the line normal to the plane, and is described by the plane's Miller indices. In three-space a family of planes (a series of parallel planes) can be denoted by its Miller indices (hkl), so the family of planes has an attitude common to all its constituent planes.
Strike and dip
Many features observed in geology are planes or lines, and their orientation is commonly referred to as their attitude. These attitudes are specified with two angles.For a line, these angles are called the trend and the plunge. The trend is the compass direction of the line, and the plunge is the downward angle it makes with a horizontal plane.
For a plane, the two angles are called its strike (angle) and its dip (angle). A strike line is the intersection of a horizontal plane with the observed planar feature (and therefore a horizontal line), and the strike angle is the bearing of this line (that is, relative to geographic north
True north
True north is the direction along the earth's surface towards the geographic North Pole.True geodetic north usually differs from magnetic north , and from grid north...
or from magnetic north
Magnetic declination
Magnetic declination is the angle between magnetic north and true north. The declination is positive when the magnetic north is east of true north. The term magnetic variation is a synonym, and is more often used in navigation...
). The dip is the angle between a horizontal plane and the observed planar feature as observed in a third vertical plane perpendicular to the strike line.
Rigid body
The attitude of a rigid body is its orientation as described, for example, by the orientation of a frame fixed in the body relative to a fixed reference frame. The attitude is described by attitude coordinates, and consists of at least three coordinates. One scheme for orienting a rigid body is based upon body-axes rotation; successive rotations three times about the axes of the body's fixed reference frame, thereby establishing the body's Euler anglesEuler angles
The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body. To describe such an orientation in 3-dimensional Euclidean space three parameters are required...
. Another is based upon roll, pitch and yaw, although these terms also refer to incremental deviations from the nominal attitude
Flight dynamics
Flight dynamics is the science of air vehicle orientation and control in three dimensions. The three critical flight dynamics parameters are the angles of rotation in three dimensions about the vehicle's center of mass, known as pitch, roll and yaw .Aerospace engineers develop control systems for...
Orientation of a space
The above described geometrical meaning of the word orientation should not be confused with its meaning in the context of linear algebraLinear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, where a different orientation means a change to the mirror image
Mirror image
A mirror image is a reflected duplication of an object that appears identical but reversed. As an optical effect it results from reflection off of substances such as a mirror or water. It is also a concept in geometry and can be used as a conceptualization process for 3-D structures...
by a reflection
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
.
Formally, for any dimension, the orientation of the image of an object under a direct isometry with respect to that object is the linear part of that isometry. Thus it is an element of SO(n), or, put differently, the corresponding coset in E+(n) / T, where T is the translation group.
See also
- Euler's rotation theoremEuler's rotation theoremIn geometry, Euler's rotation theorem states that, in three-dimensional space, any displacement of a rigid body such that a point on the rigid body remains fixed, is equivalent to a single rotation about some axis that runs through the fixed point. It also means that the composition of two...
- Flight dynamics (spacecraft)
- GyroscopeGyroscopeA gyroscope is a device for measuring or maintaining orientation, based on the principles of angular momentum. In essence, a mechanical gyroscope is a spinning wheel or disk whose axle is free to take any orientation...
- Plane of rotationPlane of rotationIn geometry, a plane of rotation is an abstract object used to describe or visualise rotations in space. In three dimensions it is an alternative to the axis of rotation, but unlike the axis of rotation it can be used in other dimensions, such as two, four or more dimensions.Mathematically such...
- Rotation representation (mathematics)Rotation representation (mathematics)In geometry a rotation representation expresses a rotation as a mathematical transformation. In physics, this concept extends to classical mechanics where rotational kinematics is the science of describing with numbers the purely rotational motion of an object.According to Euler's rotation theorem...
- Triad MethodTriad MethodThe Triad Method, also known as the algebraic method, is a method for calculating the inclination of an object based on two known vectors in relation to that object's axis system. It was developed in 1964 by Harold D. Black and first published in the Journal of the American Institute of Aeronautics...

