
Quadratic eigenvalue problem
Encyclopedia
In mathematics, the quadratic eigenvalue problem (QEP), is to find scalar
eigenvalues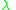 , left eigenvectors
, left eigenvectors 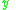 and right eigenvectors
and right eigenvectors  such that
such that
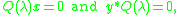
where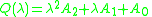 , with matrix coefficients
, with matrix coefficients 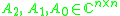 and we require that
and we require that 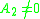 , (so that we have a nonzero leading coefficient). There are
, (so that we have a nonzero leading coefficient). There are 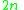 eigenvalues that may be infinite or finite, and possibly zero. This is a special case of a nonlinear eigenproblem.
eigenvalues that may be infinite or finite, and possibly zero. This is a special case of a nonlinear eigenproblem. 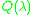 is also known as a quadratic matrix polynomial.
is also known as a quadratic matrix polynomial.
. In this case the quadratic,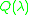 has the form
has the form 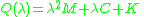 , where
, where 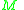 is the mass matrix
is the mass matrix
, is the damping matrix
is the damping matrix
and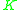 is the stiffness matrix.
is the stiffness matrix.
Other applications include vibro-acoustics and fluid dynamics.
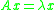 and
and 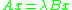
are based on transforming the problem to Schur or Generalized Schur form. However, there is no analogous form for quadratic matrix polynomials.
One approach is to transform the quadratic matrix polynomial to a linear matrix pencil (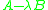 ), and solve a generalized
), and solve a generalized
eigenvalue problem. Once eigenvalues and eigenvectors of the linear problem have been determined, eigenvectors and eigenvalues of the quadratic can be determined.
The most common linearization is the first companion linearization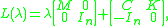
where is the
is the  -by-
-by- identity matrix, with corresponding eigenvector
identity matrix, with corresponding eigenvector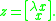
We solve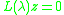 for
for 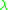 and
and  , for example by computing the Generalized Schur form. We can then
, for example by computing the Generalized Schur form. We can then
take the first components of
components of  as the eigenvector
as the eigenvector  of the original quadratic
of the original quadratic 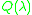 .
.
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
eigenvalues
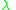 , left eigenvectors
, left eigenvectors 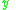 and right eigenvectors
and right eigenvectors  such that
such that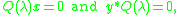
where
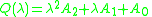 , with matrix coefficients
, with matrix coefficients 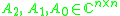 and we require that
and we require that 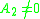 , (so that we have a nonzero leading coefficient). There are
, (so that we have a nonzero leading coefficient). There are 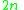 eigenvalues that may be infinite or finite, and possibly zero. This is a special case of a nonlinear eigenproblem.
eigenvalues that may be infinite or finite, and possibly zero. This is a special case of a nonlinear eigenproblem. 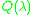 is also known as a quadratic matrix polynomial.
is also known as a quadratic matrix polynomial.Applications
A QEP can result in part of the dynamic analysis of structures discretized by the finite element methodFinite element method
The finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
. In this case the quadratic,
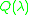 has the form
has the form 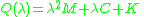 , where
, where 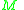 is the mass matrix
is the mass matrixMass matrix
In computational mechanics, a mass matrix is a generalization of the concept of mass to generalized coordinates. For example, consider a two-body particle system in one dimension...
,
 is the damping matrix
is the damping matrixDamping matrix
In applied mathematics, a damping matrix is a matrix corresponding to any of certain systems of linear ordinary differential equations.A damping matrix is defined as follows...
and
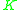 is the stiffness matrix.
is the stiffness matrix.Other applications include vibro-acoustics and fluid dynamics.
Methods of Solution
Direct methods for solving the standard or generalized eigenvalue problems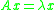 and
and 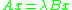
are based on transforming the problem to Schur or Generalized Schur form. However, there is no analogous form for quadratic matrix polynomials.
One approach is to transform the quadratic matrix polynomial to a linear matrix pencil (
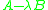 ), and solve a generalized
), and solve a generalizedeigenvalue problem. Once eigenvalues and eigenvectors of the linear problem have been determined, eigenvectors and eigenvalues of the quadratic can be determined.
The most common linearization is the first companion linearization
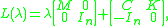
where
 is the
is the  -by-
-by- identity matrix, with corresponding eigenvector
identity matrix, with corresponding eigenvector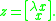
We solve
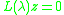 for
for 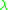 and
and  , for example by computing the Generalized Schur form. We can then
, for example by computing the Generalized Schur form. We can thentake the first
 components of
components of  as the eigenvector
as the eigenvector  of the original quadratic
of the original quadratic 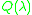 .
.

