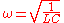Angular frequency
Encyclopedia
In physics
, angular frequency ω (also referred to by the terms angular speed, radial frequency, circular frequency, orbital frequency, and radian frequency) is a scalar measure of rotation rate. Angular frequency (or angular speed) is the magnitude of the vector quantity angular velocity
. The term angular frequency vector is sometimes used as a synonym for the vector quantity angular velocity
is sometimes used as a synonym for the vector quantity angular velocity
.
One revolution is equal to 2π radian
s, hence
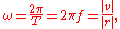
where
units, angular frequency is normally presented in radian
s per second
, even when it does not express a rotational value. From the perspective of dimensional analysis
, the unit Hertz
(Hz) is also correct, but in practice it is only used for ordinary frequency f, and almost never for ω. This convention helps avoid confusion.
In digital signal processing
, the angular frequency may be normalized by the sampling rate
, yielding the normalized frequency
.
For example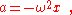
where x is displacement from an equilibrium position.
Using 'ordinary' revolutions-per-second frequency, this equation would be

where
This is referred to as the natural frequency (which can sometimes be denoted as ω0).
equals the square root of the inverse of capacitance
(C measured in farad
s), times the inductance
of the circuit (L in henrys).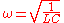
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, angular frequency ω (also referred to by the terms angular speed, radial frequency, circular frequency, orbital frequency, and radian frequency) is a scalar measure of rotation rate. Angular frequency (or angular speed) is the magnitude of the vector quantity angular velocity
Angular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
. The term angular frequency vector
 is sometimes used as a synonym for the vector quantity angular velocity
is sometimes used as a synonym for the vector quantity angular velocityAngular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
.
One revolution is equal to 2π radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s, hence
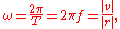
where
- ω is the angular frequency or angular speed (measured in radians per second),
- T is the periodFrequencyFrequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
(measured in secondSecondThe second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....
s), - f is the ordinary frequencyFrequencyFrequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
(measured in hertzHertzThe hertz is the SI unit of frequency defined as the number of cycles per second of a periodic phenomenon. One of its most common uses is the description of the sine wave, particularly those used in radio and audio applications....
) (sometimes symbolised with νNu (letter)Nu , is the 13th letter of the Greek alphabet. In the system of Greek numerals it has a value of 50...
), - v is the tangential velocityVelocityIn physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
of a point about the axis of rotation (measured in meters per secondMetre per secondMetre per second is an SI derived unit of both speed and velocity , defined by distance in metres divided by time in seconds....
), - r is the radiusRadiusIn classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
of rotation (measured in meters).
Units
In SISi
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
units, angular frequency is normally presented in radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s per second
Second
The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....
, even when it does not express a rotational value. From the perspective of dimensional analysis
Dimensional analysis
In physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
, the unit Hertz
Hertz
The hertz is the SI unit of frequency defined as the number of cycles per second of a periodic phenomenon. One of its most common uses is the description of the sine wave, particularly those used in radio and audio applications....
(Hz) is also correct, but in practice it is only used for ordinary frequency f, and almost never for ω. This convention helps avoid confusion.
In digital signal processing
Digital signal processing
Digital signal processing is concerned with the representation of discrete time signals by a sequence of numbers or symbols and the processing of these signals. Digital signal processing and analog signal processing are subfields of signal processing...
, the angular frequency may be normalized by the sampling rate
Sampling rate
The sampling rate, sample rate, or sampling frequency defines the number of samples per unit of time taken from a continuous signal to make a discrete signal. For time-domain signals, the unit for sampling rate is hertz , sometimes noted as Sa/s...
, yielding the normalized frequency
Normalized frequency (digital signal processing)
In digital signal processing, the normalized frequency of a periodic signal is its frequency expressed in units of cycles per sample, rather than in the usual SI units of hertz...
.
For example
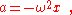
where x is displacement from an equilibrium position.
Using 'ordinary' revolutions-per-second frequency, this equation would be

Oscillations of a spring
Another often encountered expression when dealing with small oscillations or where damping is negligible is:
where
- k is the spring constant
- m is the mass of the object.
This is referred to as the natural frequency (which can sometimes be denoted as ω0).
LC Circuits
The resonant angular frequency in an LC circuitLC circuit
An LC circuit, also called a resonant circuit or tuned circuit, consists of an inductor, represented by the letter L, and a capacitor, represented by the letter C...
equals the square root of the inverse of capacitance
Capacitance
In electromagnetism and electronics, capacitance is the ability of a capacitor to store energy in an electric field. Capacitance is also a measure of the amount of electric potential energy stored for a given electric potential. A common form of energy storage device is a parallel-plate capacitor...
(C measured in farad
Farad
The farad is the SI unit of capacitance. The unit is named after the English physicist Michael Faraday.- Definition :A farad is the charge in coulombs which a capacitor will accept for the potential across it to change 1 volt. A coulomb is 1 ampere second...
s), times the inductance
Inductance
In electromagnetism and electronics, inductance is the ability of an inductor to store energy in a magnetic field. Inductors generate an opposing voltage proportional to the rate of change in current in a circuit...
of the circuit (L in henrys).