Mass matrix
Encyclopedia
In computational mechanics
, a mass matrix is a generalization of the concept of mass
to generalized coordinates
. For example, consider a two-body particle system in one dimension. The position of such a system has two degrees of freedom, the position of each particle, which can be described by the generalized position vector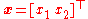
.
Supposing the particles have masses,
and 
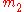. We can write Newton's second law
for each particle as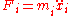
and the kinetic energy
of the system as
Putting the masses into the matrix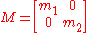
,
the same equations of motion for the two-particle system become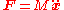
and the total kinetic energy
is given by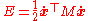
.
The structure of the mass matrix becomes more complicated in more dimensions. For example, in two dimensions, there are two degrees of freedom for a given particle, so if the ith particle corresponds to degree of freedom j and j+1, then
For example, in two dimensions the two-body system has 4 degrees of freedom (in Cartesian coordinates these would be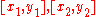
). Then, the generalized position vector would be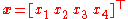
and the mass matrix would be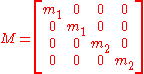
For applications in which mass is distributed such as rigid-body dynamics, there may be off-diagonal terms. For example, in one dimension if two particles with mass are connected by an ideal spring with a uniformly distributed mass, the effective acceleration of all points along the spring would correspond to differential mass elements, the acceleration of which would interpolate between the velocities of the two particles.
For discrete approximations of continuum mechanics
as in the finite element method
, there may be more than one way to construct the mass matrix, depending on desired computational and accuracy performance. For example, a lumped-mass method, in which the deformation of each element is ignored, creates a diagonal mass matrix and negates the need to integrate mass across the deformed element.
Computational mechanics
Computational mechanics is the discipline concerned with the use of computational methods to study phenomena governed by the principles of mechanics. Before the emergence of computational science as a "third way" besides theoretical and experimental sciences, computational mechanics was widely...
, a mass matrix is a generalization of the concept of mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
to generalized coordinates
Generalized coordinates
In the study of multibody systems, generalized coordinates are a set of coordinates used to describe the configuration of a system relative to some reference configuration....
. For example, consider a two-body particle system in one dimension. The position of such a system has two degrees of freedom, the position of each particle, which can be described by the generalized position vector
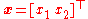.Supposing the particles have masses,
and 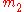. We can write Newton's second lawNewton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
for each particle as
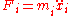
and the kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
of the system as
Putting the masses into the matrix
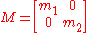,the same equations of motion for the two-particle system become
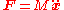
and the total kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
is given by
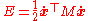.The structure of the mass matrix becomes more complicated in more dimensions. For example, in two dimensions, there are two degrees of freedom for a given particle, so if the ith particle corresponds to degree of freedom j and j+1, then
For example, in two dimensions the two-body system has 4 degrees of freedom (in Cartesian coordinates these would be
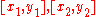). Then, the generalized position vector would be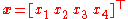and the mass matrix would be
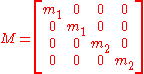
For applications in which mass is distributed such as rigid-body dynamics, there may be off-diagonal terms. For example, in one dimension if two particles with mass are connected by an ideal spring with a uniformly distributed mass, the effective acceleration of all points along the spring would correspond to differential mass elements, the acceleration of which would interpolate between the velocities of the two particles.
For discrete approximations of continuum mechanics
Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
as in the finite element method
Finite element method
The finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
, there may be more than one way to construct the mass matrix, depending on desired computational and accuracy performance. For example, a lumped-mass method, in which the deformation of each element is ignored, creates a diagonal mass matrix and negates the need to integrate mass across the deformed element.