Constant term
Encyclopedia
In mathematics
, a constant term is a term
in an algebraic expression
has a value that is constant
or cannot change, because it does not contain any modifiable variables
. For example, in the quadratic polynomial
the 3 is a constant term.
After like terms are combined, an algebraic expression will have at most one constant term. Thus, it is common to speak of the quadratic polynomial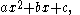
where x is the variable, and has a constant term of c. If c = 0, then the constant term will not actually appear when the quadratic is written.
It is notable that a term that is constant, with a constant as a multiplicative coefficient added to it (although this expression could be more simply written as their product), still constitutes a constant term as a variable is still not present in the new term. Although the expression is modified, the term (and coefficient) itself classifies as constant. However, should this introduced coefficient contain a variable, while the original number has a constant meaning, this has no bearing if the new term stays constant as the introduced coefficient will always override the constant expression - for example, in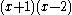
when x is multiplied by 2, the result, 2x, is not constant; while 1 * -2 is -2 and still a constant.
Any polynomial
written in standard form has a unique constant term, which can be considered a coefficient
of x0. In particular, the constant term will always be the lowest degree
term of the polynomial. This also applies to multivariate polynomials. For example, the polynomial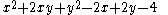
has a constant term of −4, which can be considered to be the coefficient of x0y0, where the variables are become eliminated by exponentiated to 0 (any number exponentiated to 0 becomes 1). For any polynomial, the constant term can be obtained by substituting in 0 instead of each variable; thus, eliminating each variable. The concept of exponentiation to 0 can be extended to power series and other types of series, for example in this power series: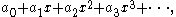
a0 is the constant term. In general a constant term is one that does not involve any variables at all. However in expressions that involve terms with other types of factors than constants and powers of variables, the notion of constant term cannot be used in this sense, since that would lead to calling "4" the constant term of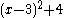
, whereas substituting 0 for x in this polynomial makes it evaluate to 13.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a constant term is a term
Term (mathematics)
A term is a mathematical expression which may form a separable part of an equation, a series, or another expression.-Definition:In elementary mathematics, a term is either a single number or variable, or the product of several numbers or variables separated from another term by a + or - sign in an...
in an algebraic expression
Expression (mathematics)
In mathematics, an expression is a finite combination of symbols that is well-formed according to rules that depend on the context. Symbols can designate numbers , variables, operations, functions, and other mathematical symbols, as well as punctuation, symbols of grouping, and other syntactic...
has a value that is constant
Constant function
In mathematics, a constant function is a function whose values do not vary and thus are constant. For example the function f = 4 is constant since f maps any value to 4...
or cannot change, because it does not contain any modifiable variables
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
. For example, in the quadratic polynomial
Quadratic polynomial
In mathematics, a quadratic polynomial or quadratic is a polynomial of degree two, also called second-order polynomial. That means the exponents of the polynomial's variables are no larger than 2...
the 3 is a constant term.
After like terms are combined, an algebraic expression will have at most one constant term. Thus, it is common to speak of the quadratic polynomial
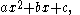
where x is the variable, and has a constant term of c. If c = 0, then the constant term will not actually appear when the quadratic is written.
It is notable that a term that is constant, with a constant as a multiplicative coefficient added to it (although this expression could be more simply written as their product), still constitutes a constant term as a variable is still not present in the new term. Although the expression is modified, the term (and coefficient) itself classifies as constant. However, should this introduced coefficient contain a variable, while the original number has a constant meaning, this has no bearing if the new term stays constant as the introduced coefficient will always override the constant expression - for example, in
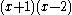when x is multiplied by 2, the result, 2x, is not constant; while 1 * -2 is -2 and still a constant.Any polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
written in standard form has a unique constant term, which can be considered a coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
of x0. In particular, the constant term will always be the lowest degree
Degree of a polynomial
The degree of a polynomial represents the highest degree of a polynominal's terms , should the polynomial be expressed in canonical form . The degree of an individual term is the sum of the exponents acting on the term's variables...
term of the polynomial. This also applies to multivariate polynomials. For example, the polynomial
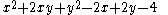
has a constant term of −4, which can be considered to be the coefficient of x0y0, where the variables are become eliminated by exponentiated to 0 (any number exponentiated to 0 becomes 1). For any polynomial, the constant term can be obtained by substituting in 0 instead of each variable; thus, eliminating each variable. The concept of exponentiation to 0 can be extended to power series and other types of series, for example in this power series:
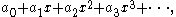
a0 is the constant term. In general a constant term is one that does not involve any variables at all. However in expressions that involve terms with other types of factors than constants and powers of variables, the notion of constant term cannot be used in this sense, since that would lead to calling "4" the constant term of
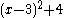, whereas substituting 0 for x in this polynomial makes it evaluate to 13.