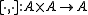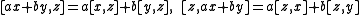Algebra (ring theory)
Encyclopedia
In mathematics
, specifically in ring theory
, an algebra over a commutative ring is a generalization of the concept of an algebra over a field
, where the base field
K is replaced by a commutative ring
R.
In this article, all rings are assumed to be unital.
A together with a binary operation
[·, ·]
called A-multiplication, which satisfies the following axiom:
under A-multiplication (it satisfies associativity and it has an identity), then the R-algebra is called an associative algebra
. An associative algebra forms a ring over R and provides a generalization of a ring. An equivalent definition of an associative R-algebra is a ring homomorphism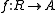 such that the image of f is contained in the center of A.
such that the image of f is contained in the center of A.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in ring theory
Ring theory
In abstract algebra, ring theory is the study of rings—algebraic structures in which addition and multiplication are defined and have similar properties to those familiar from the integers...
, an algebra over a commutative ring is a generalization of the concept of an algebra over a field
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
, where the base field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K is replaced by a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
R.
In this article, all rings are assumed to be unital.
Formal Definition
Let R be a commutative ring. An algebra is an R-moduleModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
A together with a binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
[·, ·]
called A-multiplication, which satisfies the following axiom:
- BilinearityBilinear operatorIn mathematics, a bilinear operator is a function combining elements of two vector spaces to yield an element of a third vector space that is linear in each of its arguments. Matrix multiplication is an example.-Definition:...
:
- for all scalars a, b in R and all elements x, y, z in A.
Associative Algebras
If A is a monoidMonoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
under A-multiplication (it satisfies associativity and it has an identity), then the R-algebra is called an associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
. An associative algebra forms a ring over R and provides a generalization of a ring. An equivalent definition of an associative R-algebra is a ring homomorphism
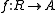 such that the image of f is contained in the center of A.
such that the image of f is contained in the center of A.See also
- associative algebraAssociative algebraIn mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
- commutative algebraCommutative algebraCommutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
- Lie algebraLie algebraIn mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
- semiringSemiringIn abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse...
- split-biquaternion (example)
- Example of a non-associative algebra (example)