
Chromatic polynomial
Encyclopedia
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
studied in algebraic graph theory
Algebraic graph theory
Algebraic graph theory is a branch of mathematics in which algebraic methods are applied to problems about graphs. This is in contrast to geometric, combinatoric, or algorithmic approaches...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
. It counts the number of graph coloring
Graph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
s as a function of the number of colors and was originally defined by George David Birkhoff
George David Birkhoff
-External links:* − from National Academies Press, by Oswald Veblen....
to attack the four color problem. It was generalised to the Tutte polynomial
Tutte polynomial
The Tutte polynomial, also called the dichromate or the Tutte–Whitney polynomial, is a polynomial in two variables which plays an important role in graph theory, a branch of mathematics and theoretical computer science...
by H. Whitney and W. T. Tutte
W. T. Tutte
William Thomas Tutte, OC, FRS, known as Bill Tutte, was a British, later Canadian, codebreaker and mathematician. During World War II he made a brilliant and fundamental advance in Cryptanalysis of the Lorenz cipher, a major German code system, which had a significant impact on the Allied...
, linking it to the Potts model
Potts model
In statistical mechanics, the Potts model, a generalization of the Ising model, is a model of interacting spins on a crystalline lattice. By studying the Potts model, one may gain insight into the behaviour of ferromagnets and certain other phenomena of solid state physics...
of statistical physics
Statistical physics
Statistical physics is the branch of physics that uses methods of probability theory and statistics, and particularly the mathematical tools for dealing with large populations and approximations, in solving physical problems. It can describe a wide variety of fields with an inherently stochastic...
.
History
George David BirkhoffGeorge David Birkhoff
-External links:* − from National Academies Press, by Oswald Veblen....
introduced the chromatic polynomial in 1912, defining it only for planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
s, in an attempt to prove the four color theorem
Four color theorem
In mathematics, the four color theorem, or the four color map theorem states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color...
. If
 denotes the number of proper colorings of
denotes the number of proper colorings of  with
with  colors then one could establish the four color theorem by showing
colors then one could establish the four color theorem by showing  for all planar graphs
for all planar graphs  . In this way he hoped to apply the powerful tools of analysis and algebra for studying the roots of polynomials to the combinatorial coloring problem.
. In this way he hoped to apply the powerful tools of analysis and algebra for studying the roots of polynomials to the combinatorial coloring problem.Hassler Whitney
Hassler Whitney
Hassler Whitney was an American mathematician. He was one of the founders of singularity theory, and did foundational work in manifolds, embeddings, immersions, and characteristic classes.-Work:...
generalised Birkhoff’s polynomial from the planar case to general graphs in 1932. In 1968 Read asked which polynomials are the chromatic polynomials of some graph, a question that remains open, and introduced the concept of chromatically equivalent graphs. Today, chromatic polynomials are one of the central objects of algebraic graph theory
Algebraic graph theory
Algebraic graph theory is a branch of mathematics in which algebraic methods are applied to problems about graphs. This is in contrast to geometric, combinatoric, or algorithmic approaches...
Definition

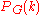 ,
, 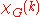 , or
, or  , and sometimes in the form
, and sometimes in the form  , where it is understood that for fixed
, where it is understood that for fixed  the function is a polynomial in
the function is a polynomial in  , the number of colors.
, the number of colors.For example, the path graph
Path graph
In the mathematical field of graph theory, a path graph or linear graph is a particularly simple example of a tree, namely a tree with two or more vertices that is not branched at all, that is, contains only vertices of degree 2 and 1...
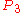 on 3 vertices cannot be colored at all with 0 or 1 colors. With 2 colors, it can be colored in 2 ways. With 3 colors, it can be colored in 12 ways.
on 3 vertices cannot be colored at all with 0 or 1 colors. With 2 colors, it can be colored in 2 ways. With 3 colors, it can be colored in 12 ways.
Available colors 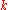 |
0 | 1 | 2 | 3 |
Number of colorings 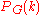 |
0 | 0 | 2 | 12 |
The chromatic polynomial is defined as the unique interpolating polynomial of degree
 through the points
through the points 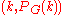 for
for 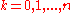 , where
, where  is the number of vertices in
is the number of vertices in  .
.For the example graph,
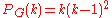 , and indeed
, and indeed  .
.The chromatic polynomial includes at least as much information about the colorability of
 as does the chromatic number. Indeed, the chromatic number is the smallest positive integer that is not a root of the chromatic polynomial,
as does the chromatic number. Indeed, the chromatic number is the smallest positive integer that is not a root of the chromatic polynomial,
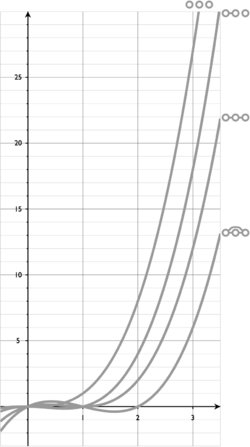
Examples
Triangle  |
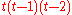 |
| Path graph Path graph In the mathematical field of graph theory, a path graph or linear graph is a particularly simple example of a tree, namely a tree with two or more vertices that is not branched at all, that is, contains only vertices of degree 2 and 1... 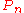 |
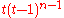 |
| Complete graph Complete graph In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:... 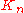 |
 |
Tree with  vertices vertices |
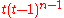 |
| Cycle Cycle graph In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn... 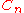 |
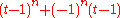 |
| Petersen graph Petersen graph In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it... |
 |
Properties
For fixed on
on  vertices, the chromatic polynomial
vertices, the chromatic polynomial 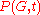 is in fact a polynomial; it has degree
is in fact a polynomial; it has degree  . Nonisomorphic graphs may have the same chromatic polynomial.
. Nonisomorphic graphs may have the same chromatic polynomial.By definition, evaluating the chromatic polynomial in
 yields the number of
yields the number of 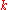 -colorings of
-colorings of  for
for 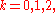 …
… . Perhaps surprisingly, the same holds for any
. Perhaps surprisingly, the same holds for any  , and besides,
, and besides,  yields the number of acyclic orientations
yields the number of acyclic orientationsDirected acyclic graph
In mathematics and computer science, a directed acyclic graph , is a directed graph with no directed cycles. That is, it is formed by a collection of vertices and directed edges, each edge connecting one vertex to another, such that there is no way to start at some vertex v and follow a sequence of...
of
 . Furthermore,
. Furthermore,the derivative evaluated at 1,
 equals the chromatic invariant
equals the chromatic invariant 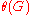 up to sign.
up to sign.If
 has
has  vertices,
vertices,  edges, and
edges, and  components
componentsConnected component (graph theory)
In graph theory, a connected component of an undirected graph is a subgraph in which any two vertices are connected to each other by paths, and which is connected to no additional vertices. For example, the graph shown in the illustration on the right has three connected components...
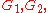 …,
…,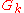 , then
, then
- The coefficient of
 in
in 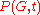 is 1.
is 1. - The coefficient of
 in
in  is .
is . - The coefficients of
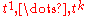 are all nonzero.
are all nonzero. - The coefficient of
 is nonzero.
is nonzero. -

- The coefficients of every chromatic polynomial alternate in signs.
A graph G with
 vertices is a tree if and only if
vertices is a tree if and only if  .
.Chromatic equivalence
 vertices have the same chromatic polynomial; in particular,
vertices have the same chromatic polynomial; in particular, 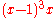 is the chromatic polynomial of both the claw graph
is the chromatic polynomial of both the claw graphClaw (graph theory)
In graph theory, an area of mathematics, a claw-free graph is a graph that does not have a claw as an induced subgraph.A claw is another name for the complete bipartite graph K1,3...
and the path graph
Path graph
In the mathematical field of graph theory, a path graph or linear graph is a particularly simple example of a tree, namely a tree with two or more vertices that is not branched at all, that is, contains only vertices of degree 2 and 1...
on 4 vertices.
Chromatic uniqueness
A graph is chromatically unique if it is determined by its chromatic polynomial, up to isomorphism. In other words, is chromatically unique if
is chromatically unique if  implies that
implies that  and
and  are isomorphic. All Cycle graph
are isomorphic. All Cycle graphCycle graph
In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...
s are chromatically unique.
Chromatic roots
A root (or zero) of a chromatic polynomial, called a “chromatic root”, is a value where
where  . Chromatic roots have been very well studied, in fact, Birkhoff’s original motivation for defining the chromatic polynomial was to show that for planar graphs,
. Chromatic roots have been very well studied, in fact, Birkhoff’s original motivation for defining the chromatic polynomial was to show that for planar graphs, 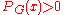 for
for  ≥ 4. This would have established the four color theorem
≥ 4. This would have established the four color theoremFour color theorem
In mathematics, the four color theorem, or the four color map theorem states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color...
.
No graph can be 0-colored, so 0 is always a chromatic root. Only edgeless graphs can be 1-colored, so 1 is a chromatic root for every graph with at least an edge. On the other hand, except for these two points, no graph can have a chromatic root at a real number smaller than or equal to 32/27. A result of Tutte connects the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
 with the study of chromatic roots, showing that chromatic roots exist very close to
with the study of chromatic roots, showing that chromatic roots exist very close to 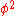 :
:If
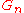 is a planar triangulation of a sphere then
is a planar triangulation of a sphere then 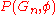 ≤
≤ 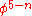 . While the real line thus has large parts that contain no chromatic roots for any graph, every point in the complex plane
. While the real line thus has large parts that contain no chromatic roots for any graph, every point in the complex planeComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
is arbitrarily close to a chromatic root in the sense that there exists an infinite family of graphs whose chromatic roots are dense in the complex plane.
Algorithms
 with
with  vertices.
vertices.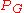
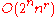 for some constant
for some constant 
Sharp-P
In computational complexity theory, the complexity class #P is the set of the counting problems associated with the decision problems in the set NP. More formally, #P is the class of function problems of the form "compute ƒ," where ƒ is the number of accepting paths of a nondeterministic...
-hard
 with
with  vertices.
vertices.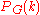
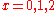 .
.  for
for  . Otherwise
. Otherwise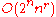 for some constant
for some constant 
Sharp-P
In computational complexity theory, the complexity class #P is the set of the counting problems associated with the decision problems in the set NP. More formally, #P is the class of function problems of the form "compute ƒ," where ƒ is the number of accepting paths of a nondeterministic...
-hard unless
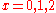

Computational problems associated with the chromatic polynomial include
- finding the chromatic polynomial
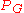 of a given graph
of a given graph  , for example finding its coefficients
, for example finding its coefficients - evaluating
 at a fixed point
at a fixed point 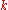 for given
for given  . When
. When 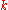 is a natural number, this problem is normally viewed as computing the number of
is a natural number, this problem is normally viewed as computing the number of  -colorings of a given graph. For example, this includes the problem #3-coloring of counting the number of 3-colorings, a canonical problem in the study of complexity of counting, complete for the counting class #PSharp-PIn computational complexity theory, the complexity class #P is the set of the counting problems associated with the decision problems in the set NP. More formally, #P is the class of function problems of the form "compute ƒ," where ƒ is the number of accepting paths of a nondeterministic...
-colorings of a given graph. For example, this includes the problem #3-coloring of counting the number of 3-colorings, a canonical problem in the study of complexity of counting, complete for the counting class #PSharp-PIn computational complexity theory, the complexity class #P is the set of the counting problems associated with the decision problems in the set NP. More formally, #P is the class of function problems of the form "compute ƒ," where ƒ is the number of accepting paths of a nondeterministic...
.
The first problem is more general because if we knew the coefficients of
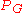 we could evaluate it at any point in polynomial time because the degree is
we could evaluate it at any point in polynomial time because the degree is  . The difficulty of the second type of problem depends strongly on the value of
. The difficulty of the second type of problem depends strongly on the value of 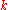 and has been intensively studied in computational complexity
and has been intensively studied in computational complexityComputational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
.
Efficient algorithms
For some basic graph classes, closed formulas for the chromatic polynomial are known. For instance this is true for trees and cliques, as listed in the table above.Polynomial time algorithms are known for computing the chromatic polynomial for wider classes of graphs, including chordal graph
Chordal graph
In the mathematical area of graph theory, a graph is chordal if each of its cycles of four or more nodes has a chord, which is an edge joining two nodes that are not adjacent in the cycle. An equivalent definition is that any chordless cycles have at most three nodes...
s and graphs of bounded clique-width
Clique-width
In graph theory, the clique-width of a graph G is the minimum number of labels needed to construct G by means of the following 4 operations :#Creation of a new vertex v with label i...
. The latter class includes cograph
Cograph
In graph theory, a cograph, or complement-reducible graph, or P4-free graph, is a graph that can be generated from the single-vertex graph K1 by complementation and disjoint union...
s and graphs of bounded tree-width, such as outerplanar graph
Outerplanar graph
In graph theory, an undirected graph is an outerplanar graph if it can be drawn in the plane without crossings in such a way that all of the vertices belong to the unbounded face of the drawing. That is, no vertex is totally surrounded by edges...
s.
Deletion–contraction
A recursive way of computing the chromatic polynomial is based on edge contractionEdge contraction
In graph theory, an edge contraction is an operation which removes an edge from a graph while simultaneously merging together the two vertices it previously connected. Edge contraction is a fundamental operation in the theory of graph minors...
: for a pair of vertices
 and
and  the graph
the graph 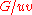 is obtained by merging the two vertices and removing any edges between them.
is obtained by merging the two vertices and removing any edges between them.Then the chromatic polynomial satisfies the recurrence relation

where
 and
and  are adjacent vertices and
are adjacent vertices and  is the graph with the edge
is the graph with the edge  removed. Equivalently,
removed. Equivalently,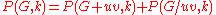
if
 and
and  are not adjacent and
are not adjacent and  is the graph with the edge
is the graph with the edge  added. In the first form, the recurrence terminates in a collection of empty graphs. In the second form, it terminates in a collection of complete graphs. These recurrences are also called the Fundamental Reduction Theorem
added. In the first form, the recurrence terminates in a collection of empty graphs. In the second form, it terminates in a collection of complete graphs. These recurrences are also called the Fundamental Reduction TheoremTutte’s curiosity about which other graph properties satisfied such recurrences led him to discover a bivariate generalization of the chromatic polynomial, the Tutte polynomial
Tutte polynomial
The Tutte polynomial, also called the dichromate or the Tutte–Whitney polynomial, is a polynomial in two variables which plays an important role in graph theory, a branch of mathematics and theoretical computer science...
.
The expressions give rise to a recursive procedure, called the deletion–contraction algorithm, which forms the basis of many algorithms for graph coloring. The ChromaticPolynomial function in the computer algebra system Mathematica
Mathematica
Mathematica is a computational software program used in scientific, engineering, and mathematical fields and other areas of technical computing...
uses the second recurrence if the graph is dense, and the first recurrence if the graph is sparse The worst case running time of either formula satisfies the same recurrence relation as the Fibonacci numbers, so in the worst case, the algorithm runs in time within a polynomial factor of
 . The analysis can be improved to within a polynomial factor of the number
. The analysis can be improved to within a polynomial factor of the number 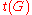 of spanning trees
of spanning treesSpanning tree (mathematics)
In the mathematical field of graph theory, a spanning tree T of a connected, undirected graph G is a tree composed of all the vertices and some of the edges of G. Informally, a spanning tree of G is a selection of edges of G that form a tree spanning every vertex...
of the input graph.
In practice, branch and bound
Branch and bound
Branch and bound is a general algorithm for finding optimal solutions of various optimization problems, especially in discrete and combinatorial optimization...
strategies and graph isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
rejection are employed to avoid some recursive calls, the running time depends on the heuristic used to pick the vertex pair.
Computational complexity
The problem of computing the number of 3-colorings of a given graph is a canonical example of a #PSharp-P
In computational complexity theory, the complexity class #P is the set of the counting problems associated with the decision problems in the set NP. More formally, #P is the class of function problems of the form "compute ƒ," where ƒ is the number of accepting paths of a nondeterministic...
-complete problem, so the problem of computing the coefficients of the chromatic polynomial is #P-hard. Similarly, evaluating
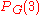 for given
for given  is #P-complete.
is #P-complete.On the other hand, for
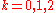 it is easy to compute
it is easy to compute 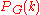 , so the corresponding problems are polynomial-time computable. For integers
, so the corresponding problems are polynomial-time computable. For integers  the problem is #P-hard, which is established similar to the case
the problem is #P-hard, which is established similar to the case  . In fact, it is known that
. In fact, it is known that 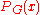 is #P-hard for all
is #P-hard for all  (including negative integers and non-integers) except for the three “easy points” Thus, from the perspective of #P-hardness, the complexity of computing the chromatic polynomial is completely understood.
(including negative integers and non-integers) except for the three “easy points” Thus, from the perspective of #P-hardness, the complexity of computing the chromatic polynomial is completely understood.In the expansion
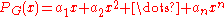 , the coefficient
, the coefficient 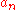 is always equal to 1, and several other properties of the coefficients are known. This raises the question if some of the coefficients are easy to compute. However the computational problem of computing the
is always equal to 1, and several other properties of the coefficients are known. This raises the question if some of the coefficients are easy to compute. However the computational problem of computing the  th coefficient of
th coefficient of 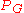 for fixed
for fixed  for given graph
for given graph  is hard for #P.
is hard for #P.No approximation algorithms for computing
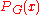 are known for any
are known for any  except for the three easy points. At the integer points
except for the three easy points. At the integer points 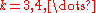 , the corresponding decision problem
, the corresponding decision problemDecision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
of deciding if a given graph can be
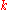 -colored is NP-hard
-colored is NP-hardNP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
. Such problems cannot be approximated to any multiplicative factor by a bounded-error probabilistic algorithm unless NP = RP, because any multiplicative approximation would distinguish the values 0 and 1, effectively solving the decision version in bounded-error probabilistic polynomial time. In particular, under the same assumption, this rules out the possibility of a fully polynomial time randomised approximation scheme (FPRAS). For other points, more complicated arguments are needed, and the question is the focus of active research. , it is known that there is no FPRAS for computing
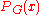 for any
for any  unless NP = RP holds.
unless NP = RP holds.External links
- PlanetMathPlanetMathPlanetMath is a free, collaborative, online mathematics encyclopedia. The emphasis is on rigour, openness, pedagogy, real-time content, interlinked content, and also community of about 24,000 people with various maths interests. Intended to be comprehensive, the project is hosted by the Digital...
Chromatic polynomial - Code for computing Tutte, Chromatic and Flow Polynomials by Gary Haggard, David J. Pearce and Gordon Royle: http://www.ecs.vuw.ac.nz/~djp/tutte/
The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.


