Horner scheme
Encyclopedia
In numerical analysis
, the Horner scheme (also known as Horner algorithm), named after William George Horner
, is an algorithm
for the efficient evaluation of polynomial
s in monomial form
. Horner's method describes a manual process by which one may approximate the roots of a polynomial equation. The Horner scheme can also be viewed as a fast algorithm for dividing a polynomial by a linear polynomial with Ruffini's rule
.
where
are real numbers, we wish to evaluate the polynomial at a specific value of x, say x0.
To accomplish this, we define a new sequence of constants as follows:
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, the Horner scheme (also known as Horner algorithm), named after William George Horner
William George Horner
William George Horner was a British mathematician and schoolmaster. The invention of the zoetrope, in 1834 and under a different name , has been attributed to him.-Life:...
, is an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
for the efficient evaluation of polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s in monomial form
Monomial basis
In mathematics a monomial basis is a way to describe uniquely a polynomial using a linear combination of monomials. This description, the monomial form of a polynomial, is often used because of the simple structure of the monomial basis....
. Horner's method describes a manual process by which one may approximate the roots of a polynomial equation. The Horner scheme can also be viewed as a fast algorithm for dividing a polynomial by a linear polynomial with Ruffini's rule
Ruffini's rule
In mathematics, Ruffini's rule allows the rapid division of any polynomial by a binomial of the form x − r. It was described by Paolo Ruffini in 1809. Ruffini's rule is a special case of synthetic division when the divisor is a linear factor. The Horner scheme is a fast algorithm for dividing...
.
Description of the algorithm
Given the polynomialwhere
are real numbers, we wish to evaluate the polynomial at a specific value of x, say x0.To accomplish this, we define a new sequence of constants as follows:
-
Then b0 is the value of p(x0).
To see why this works, note that the polynomial can be written in the form
Thus, by iteratively substituting the
into the expression,
-
Examples
Evaluate
for 
.
We use synthetic division as follows:
x₀│ x³ x² x¹ x⁰
3 │ 2 -6 2 -1
│ 6 0 6
└────────────────────────
2 0 2 5
The entries in the third row are the sum of those in the first two. Each entry in the second row is the product of the x-value (3 in this example) with the third-row entry immediately to the left. The entries in the first row are the coefficients of the polynomial to be evaluated. Then the remainder of
on division by 
is 5.
But by the remainder theorem, we know that the remainder is
. Thus 
In this example, if
we can see that 
, the entries in the third row. So, synthetic division is based on Horner Scheme.
As a consequence of the polynomial remainder theoremPolynomial remainder theoremIn algebra, the polynomial remainder theorem or little Bézout's theorem is an application of polynomial long division. It states that the remainder of a polynomial f\, divided by a linear divisor x-a\, is equal to f \,.- Example :...
, the entries in the third row are the coefficients of the second-degree polynomial, the quotient of
on division by 
.
The remainder is 5. This makes Horner's method useful for polynomial long divisionPolynomial long divisionIn algebra, polynomial long division is an algorithm for dividing a polynomial by another polynomial of the same or lower degree, a generalised version of the familiar arithmetic technique called long division...
.
Divide
by 
:
2 │ 1 -6 11 -6
│ 2 -8 6
└────────────────────────
1 -4 3 0
The quotient is
.
Let
and 
. Divide 
by 
using Horner's scheme.
2 │ 4 -6 0 3 │ -5
────┼──────────────────────┼───────
1 │ 2 -2 -1 │ 1
│ │
└──────────────────────┼───────
2 -2 -1 1 │ -4
The third row is the sum of the first two rows, divided by 2. Each entry in the second row is the product of 1 with the third-row entry to the left. The answer is
Floating point multiplication and division
Horner's method is a fast, code-efficient method for multiplication and division of binary numbers on a microcontrollerMicrocontrollerA microcontroller is a small computer on a single integrated circuit containing a processor core, memory, and programmable input/output peripherals. Program memory in the form of NOR flash or OTP ROM is also often included on chip, as well as a typically small amount of RAM...
with no hardware multiplierBinary multiplierA binary multiplier is an electronic circuit used in digital electronics, such as a computer, to multiply two binary numbers. It is built using binary adders....
. One of the binary numbers to be multiplied is represented as a trivial polynomial, where, (using the above notation): ai = 1, and x = 2. Then, x (or x to some power) is repeatedly factored out. In this binary numeral systemBinary numeral systemThe binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
(base 2), x = 2, so powers of 2 are repeatedly factored out.
Example
For example, to find the product of two numbers, (0.15625) and m:
Method
To find the product of two binary numbers, "d" and "m".- 1. A register holding the intermediate result is initialized to (d).
- 2. Begin in (m) with the least significant (rightmost) non-zero bit,
- 2b. Count (to the left) the number of bit positions to the next most significant non-zero bit. If there are no more-significant bits, then take the value of the current bit position.
- 2c. Using that value, perform a right-shift operation by that number of bits on the register holding the intermediate result
- 3. If all the non-zero bits were counted, then the intermediate result register now holds the final result. Otherwise, add (d) to the intermediate result, and continue in step #2 with the next most significant bit in (m).
Derivation
In general, for a binary number with bit values: (
) the product is:
At this stage in the algorithm, it is required that terms with zero-valued coefficients are dropped, so that only binary coefficients equal to one are counted, thus the problem of multiplication or division by zeroDivision by zeroIn mathematics, division by zero is division where the divisor is zero. Such a division can be formally expressed as a / 0 where a is the dividend . Whether this expression can be assigned a well-defined value depends upon the mathematical setting...
is not an issue, despite this implication in the factored equation:
The denominators all equal one (or the term is absent), so this reduces to:
or equivalently (as consistent with the "method" described above):
In binary (base 2) math, multiplication by a power of 2 is merely a register shiftArithmetic shiftIn computer programming, an arithmetic shift is a shift operator, sometimes known as a signed shift . For binary numbers it is a bitwise operation that shifts all of the bits of its operand; every bit in the operand is simply moved a given number of bit positions, and the vacant bit-positions are...
operation. Thus, multiplying by 2 is calculated in base-2 by an arithmetic shiftArithmetic shiftIn computer programming, an arithmetic shift is a shift operator, sometimes known as a signed shift . For binary numbers it is a bitwise operation that shifts all of the bits of its operand; every bit in the operand is simply moved a given number of bit positions, and the vacant bit-positions are...
. The factor (2−1) is a right arithmetic shiftArithmetic shiftIn computer programming, an arithmetic shift is a shift operator, sometimes known as a signed shift . For binary numbers it is a bitwise operation that shifts all of the bits of its operand; every bit in the operand is simply moved a given number of bit positions, and the vacant bit-positions are...
, a (0) results in no operation (since 20 = 1, is the multiplicative identity elementIdentity elementIn mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
), and a (21) results in a left arithmetic shift.
The multiplication product can now be quickly calculated using only arithmetic shift operations, addition and subtraction.
The method is particularly fast on processors supporting a single-instruction shift-and-addition-accumulate. Compared to a C floating-point library, Horner's method sacrifices some accuracy, however it is nominally 13 times faster (16 times faster when the "canonical signed digitCanonical signed digitIn computing canonical-signed-digit is a number system for encoding a floating-point value in a two's complement representation. This encoding contains 33% fewer zeros than the two's complement form, leading to efficient implementations of add/subtract networks in hardwired Digital signal...
" (CSD) form is used), and uses only 20% of the code space.
Polynomial root finding
Using the Horner scheme in combination with Newton's zero finding method it is possible to approximate the real roots of a polynomial. The algorithm is as follows. Given a polynomial
of degree 
with zeros 
make some initial guess 
such that 
. Now follow the steps outline below.
1. Using Newton's methodNewton's methodIn numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
find the largest zero,
of 
using the guess 
.
2. Use the Horner scheme to divide out
to obtain 
. Return to step 1 but use the polynomial 
and the initial guess 
.
These two steps are repeated until all real zeros are found for the polynomial. If the approximated zeros are not precise enough, the obtained values can be used as initial guesses for Newton's method but using the full polynomial rather than the reduced polynomials.
Example
Consider the polynomial,
which can be expanded to,
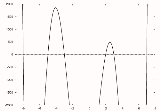
From the above we know that the largest root of this polynomial is 7 so we are able to make an initial guess of 8. Using Newton's method the first zero of 7 is found as shown in black in the figure to the right. Next
is divided by 
to obtain,
which is drawn in red in the figure to the right. Newton's method is used to find the largest zero of this polynomial with an initial guess of 7. The largest zero of this polynomial which corresponds to the second largest zero of the original polynomial is found at 3 and is circled in red. The degree 5 polynomial is now divided by
to obtain,
which is shown in yellow. The zero for this polynomial is found at 2 again using Newton's method and is circled in yellow. The Horner scheme is now used to obtain,
which is shown in green and found to have a zero at -3. This polynomial is further reduced to,
which is shown in blue and yields a zero of -5. The final root of the original polynomial may be found by either using the final zero as an initial guess for Newton's method, or by reducing
and solving the linear equation. As can be seen, the expected roots of -8, -5, -3, 2, 3, and 7 were found.
Octave implementation
The following OctaveGNU OctaveGNU Octave is a high-level language, primarily intended for numerical computations. It provides a convenient command-line interface for solving linear and nonlinear problems numerically, and for performing other numerical experiments using a language that is mostly compatible with MATLAB...
code was used in the example above to implement the Horner scheme.
function [y b] = horner(a,x)
% Input a is the polynomial coefficient vector, x the value to be evaluated at.
% The output y is the evaluated polynomial and b the divided coefficient vector.
b(1) = a(1);
for i = 2:length(a)
b(i) = a(i)+x*b(i-1);
end
y = b(length(a));
b = b(1:length(b)-1);
end
Python implementation
The following PythonPython (programming language)Python is a general-purpose, high-level programming language whose design philosophy emphasizes code readability. Python claims to "[combine] remarkable power with very clear syntax", and its standard library is large and comprehensive...
code implements the Horner scheme.
def horner(x, *args):
"""A function that implements the Horner Scheme for evaluating a
polynomial of coefficients *args in x."""
result = 0
for coefficient in args:
result = result * x + coefficient
return result
Application
The Horner scheme is often used to convert between different positional numeral systemNumeral systemA numeral system is a writing system for expressing numbers, that is a mathematical notation for representing numbers of a given set, using graphemes or symbols in a consistent manner....
s – in which case x is the base of the number system, and the ai coefficients are the digits of the base-x representation of a given number – and can also be used if x is a matrix, in which case the gain in computational efficiency is even greater. In fact, when x is a matrix, further acceleration is possible which exploits the structure of matrix multiplicationMatrix multiplicationIn mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
, and only
instead of n multiplies are needed (at the expense of requiring more storage) using the 1973 method of Paterson and Stockmeyer.
Efficiency
Evaluation using the monomial form of a degree-n polynomial requires at most n additions and (n2 + n)/2 multiplications, if powers are calculated by repeated multiplication and each monomial is evaluated individually. (This can be reduced to n additions and 2n - 1 multiplications by evaluating the powers of x iteratively.) If numerical data are represented in terms of digits (or bits), then the naive algorithm also entails storing approximately 2n times the number of bits of x (the evaluated polynomial has approximate magnitude xn, and one must also store xn itself). By contrast, Horner's scheme requires only n additions and n multiplications, and its storage requirements are only n times the number of bits of x. Alternatively, Horner's scheme can be computed with n fused multiply–adds. Horner's scheme can also be extended to evaluate the first k derivatives of the polynomial with kn additions and multiplications.
It has been shown that the Horner scheme is optimal, in the sense that any algorithm to evaluate an arbitrary polynomial must use at least as many operations. That the number of additions required is minimal was shown by Alexander OstrowskiAlexander OstrowskiAlexander Markowich Ostrowski , was a mathematician.His father Mark having been a merchant, Alexander Ostrowski attended the Kiev College of Commerce, not a high school, and thus had an insufficient qualification to be admitted to university...
in 1954; that the number of multiplications is minimal by Victor PanVictor PanVictor Ya. Pan is a Soviet and American mathematician and computer scientist. He earned his Ph.D. at Moscow University then continued at the Soviet Academy of Sciences. During that time, he published a number of significant papers and became known informally as "polynomial Pan" for his pioneering...
, in 1966. When x is a matrix, the Horner scheme is not optimal.
This assumes that the polynomial is evaluated in monomial form and no preconditioning of the representation is allowed, which makes sense if the polynomial is evaluated only once. However, if preconditioning is allowed and the polynomial is to be evaluated many times, then faster algorithms are possible. They involve a transformation of the representation of the polynomial. In general, a degree-n polynomial can be evaluated using only
multiplications and n additions (see KnuthDonald KnuthDonald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...
: The Art of Computer ProgrammingThe Art of Computer ProgrammingThe Art of Computer Programming is a comprehensive monograph written by Donald Knuth that covers many kinds of programming algorithms and their analysis....
, Vol.2).
History
Even though the algorithm is named after William George HornerWilliam George HornerWilliam George Horner was a British mathematician and schoolmaster. The invention of the zoetrope, in 1834 and under a different name , has been attributed to him.-Life:...
, who described it in 1819, the method was already known to Isaac NewtonIsaac NewtonSir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
in 1669, the Chinese mathematicianChinese mathematicsMathematics in China emerged independently by the 11th century BC. The Chinese independently developed very large and negative numbers, decimals, a place value decimal system, a binary system, algebra, geometry, and trigonometry....
Qin Jiushao in his Mathematical Treatise in Nine SectionsMathematical Treatise in Nine SectionsThe Mathematical Treatise in Nine Sections is a mathematical text written by Chinese Southern Song dynasty mathematician Qin Jiushao in the year 1247.This book contains nine chapters:#Da Yan type ;#Heaven phenomena...
in the 13th century, and even earlier to the 11th century Song dynasty mathematician Jia XianJia XianJia Xian was a Chinese mathematician from Kaifeng of the Song Dynasty, in the first half of the 11th century.-Biography:...
, and the PersianPersian peopleThe Persian people are part of the Iranian peoples who speak the modern Persian language and closely akin Iranian dialects and languages. The origin of the ethnic Iranian/Persian peoples are traced to the Ancient Iranian peoples, who were part of the ancient Indo-Iranians and themselves part of...
Muslim mathematicianIslamic mathematicsIn the history of mathematics, mathematics in medieval Islam, often termed Islamic mathematics or Arabic mathematics, covers the body of mathematics preserved and developed under the Islamic civilization between circa 622 and 1600...
Sharaf al-Dīn al-Tūsī in the 12th century. The earliest use of Horner's scheme was in The Nine Chapters on the Mathematical ArtThe Nine Chapters on the Mathematical ArtThe Nine Chapters on the Mathematical Art is a Chinese mathematics book, composed by several generations of scholars from the 10th–2nd century BCE, its latest stage being from the 1st century CE...
, a Chinese work of the Han DynastyHan DynastyThe Han Dynasty was the second imperial dynasty of China, preceded by the Qin Dynasty and succeeded by the Three Kingdoms . It was founded by the rebel leader Liu Bang, known posthumously as Emperor Gaozu of Han. It was briefly interrupted by the Xin Dynasty of the former regent Wang Mang...
(202 BC – 220 AD) edited by Liu HuiLiu HuiLiu Hui was a mathematician of the state of Cao Wei during the Three Kingdoms period of Chinese history. In 263, he edited and published a book with solutions to mathematical problems presented in the famous Chinese book of mathematic known as The Nine Chapters on the Mathematical Art .He was a...
(fl. 3rd century).
See also
- Clenshaw algorithmClenshaw algorithmIn numerical analysis, the Clenshaw algorithm is a recursive method to evaluate a linear combination of Chebyshev polynomials. In general it applies to any class of functions that can be defined by a three-term recurrence relation.-Clenshaw algorithm:...
to evaluate polynomials in Chebyshev form - De Casteljau's algorithmDe Casteljau's algorithmIn the mathematical field of numerical analysis, De Casteljau's algorithm is a recursive method to evaluate polynomials in Bernstein form or Bézier curves, named after its inventor Paul de Casteljau...
to evaluate polynomials in Bézier form - De Boor's algorithmDe Boor's algorithmIn the mathematical subfield of numerical analysis the de Boor's algorithm is a fast and numerically stable algorithm for evaluating spline curves in B-spline form. It is a generalization of the de Casteljau's algorithm for Bézier curves. The algorithm was devised by Carl R. de Boor...
to evaluate splines in B-splineB-splineIn the mathematical subfield of numerical analysis, a B-spline is a spline function that has minimal support with respect to a given degree, smoothness, and domain partition. B-splines were investigated as early as the nineteenth century by Nikolai Lobachevsky...
form - Estrin's schemeEstrin's schemeIn numerical analysis Estrin's scheme is an algorithm for numerical evaluation of polynomials.The Horner scheme for evaluation of polynomials is one of the most commonly used algorithms for this purpose and unlike Estrin's scheme it is optimal in the sense that it minimizes the number of...
that is amenable to parallelization on modern computer architectures.
External links
-