Antiderivative
Encyclopedia
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, an "anti-derivative", antiderivative, primitive integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
or indefinite integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
f is a function F whose derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
is equal to f, i.e., F ′ = f. The process of solving for antiderivatives is called antidifferentiation (or indefinite integration) and its opposite function is called differentiation, which is the process of finding a derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
. Antiderivatives are related to definite integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
s through the fundamental theorem of calculus
Fundamental theorem of calculus
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
: the definite integral of a function over an interval is equal to the difference between the values of an antiderivative evaluated at the endpoints of the interval.
The discrete equivalent of the notion of antiderivative is antidifference.
Example
The function F(x) = x3/3 is an antiderivative of f(x) = x2. As the derivative of a constantConstant function
In mathematics, a constant function is a function whose values do not vary and thus are constant. For example the function f = 4 is constant since f maps any value to 4...
is zero
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
, x2 will have an infinite
Infinity
Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
number of antiderivatives; such as (x3/3) + 0, (x3/3) + 7, (x3/3) − 42, (x3/3) + 293 etc. Thus, all the antiderivatives of x2 can be obtained by changing the value of C in F(x) = (x3/3) + C; where C is an arbitrary constant known as the constant of integration
Arbitrary constant of integration
In calculus, the indefinite integral of a given function is only defined up to an additive constant, the constant of integration. This constant expresses an ambiguity inherent in the construction of antiderivatives...
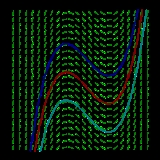
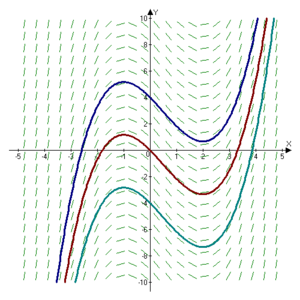
. Essentially, the graphs
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
of antiderivatives of a given function are vertical translation
Vertical translation
In function graphing, a vertical translation is a related graph which, for every point ; has a y value which differs from another graph, by exactly some constant c. For example, the antiderivatives of a family are vertical translations of each other....
s of each other; each graph's location depending upon the value
Value (mathematics)
In mathematics, value commonly refers to the 'output' of a function. In the most basic case, that of unary, single-valued functions, there is one input and one output .The function f of the example is real-valued, since each and every possible function value is real...
of C.
In physics, the integration of acceleration yields velocity plus a constant. The constant is the initial velocity term that would be lost upon taking the derivative of velocity because the derivative of a constant term is zero. This same pattern applies to further integrations and derivatives of motion (position, velocity, acceleration, and so on).
Uses and properties
Antiderivatives are important because they can be used to compute definite integrals, using the fundamental theorem of calculusFundamental theorem of calculus
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
: if F is an antiderivative of the integrable
Riemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
function f, then:
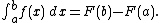
Because of this, each of the infinitely many antiderivatives of a given function f is sometimes called the "general integral" or "indefinite integral" of f and is written using the integral symbol with no bounds:

If F is an antiderivative of f, and the function f is defined on some interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
, then every other antiderivative G of f differs from F by a constant: there exists a number C such that G(x) = F(x) + C for all x. C is called the arbitrary constant of integration
Arbitrary constant of integration
In calculus, the indefinite integral of a given function is only defined up to an additive constant, the constant of integration. This constant expresses an ambiguity inherent in the construction of antiderivatives...
. If the domain of F is a disjoint union
Disjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
of two or more intervals, then a different constant of integration may be chosen for each of the intervals. For instance
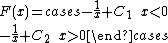
is the most general antiderivative of
 on its natural domain
on its natural domain 
Every continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
f has an antiderivative, and one antiderivative F is given by the definite integral of f with variable upper boundary:

Varying the lower boundary produces other antiderivatives (but not necessarily all possible antiderivatives). This is another formulation of the fundamental theorem of calculus
Fundamental theorem of calculus
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
.
There are many functions whose antiderivatives, even though they exist, cannot be expressed in terms of elementary functions (like polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s, exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
s, logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
s, trigonometric functions, inverse trigonometric functions and their combinations). Examples of these are
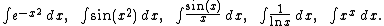
See also differential Galois theory
Differential Galois theory
In mathematics, differential Galois theory studies the Galois groups of differential equations.Whereas algebraic Galois theory studies extensions of algebraic fields, differential Galois theory studies extensions of differential fields, i.e. fields that are equipped with a derivation, D. Much of...
for a more detailed discussion.
Techniques of integration
Finding antiderivatives of elementary functions is often considerably harder than finding their derivatives. For some elementary functions, it is impossible to find an antiderivative in terms of other elementary functions. See the article on elementary functionsElementary function (differential algebra)
In mathematics, an elementary function is a function of one variable built from a finite number of exponentials, logarithms, constants, and nth roots through composition and combinations using the four elementary operations...
for further information.
We have various methods at our disposal:
- the linearity of integrationLinearity of integrationIn calculus, linearity is a fundamental property of the integral that follows from the sum rule in integration and the constant factor rule in integration. Linearity of integration is related to the linearity of summation, since integrals are thought of as infinite sums.Let ƒ and g be functions...
allows us to break complicated integrals into simpler ones - integration by substitutionIntegration by substitutionIn calculus, integration by substitution is a method for finding antiderivatives and integrals. Using the fundamental theorem of calculus often requires finding an antiderivative. For this and other reasons, integration by substitution is an important tool for mathematicians...
, often combined with trigonometric identities or the natural logarithmNatural logarithmThe natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828... - integration by partsIntegration by partsIn calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
to integrate products of functions - the inverse chain rule method, a special case of integration by substitution
- the method of partial fractions in integrationPartial fractions in integrationIn integral calculus, partial fraction expansions provide an approach to integrating a general rational function. Any rational function of a real variable can be written as the sum of a polynomial function and a finite number of algebraic fractions...
allows us to integrate all rational functionRational functionIn mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s (fractions of two polynomials) - the Risch algorithmRisch algorithmThe Risch algorithm, named after Robert Henry Risch, is an algorithm for the calculus operation of indefinite integration . The algorithm transforms the problem of integration into a problem in algebra. It is based on the form of the function being integrated and on methods for integrating rational...
- integrals can also be looked up in a table of integrals
- when integrating multiple times, we can use certain additional techniques, see for instance double integrals and polar coordinatesPolar coordinate systemIn mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a fixed point and an angle from a fixed direction....
, the Jacobian and the Stokes' theoremStokes' theoremIn differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850... - computer algebra systemComputer algebra systemA computer algebra system is a software program that facilitates symbolic mathematics. The core functionality of a CAS is manipulation of mathematical expressions in symbolic form.-Symbolic manipulations:...
s can be used to automate some or all of the work involved in the symbolic techniques above, which is particularly useful when the algebraic manipulations involved are very complex or lengthy - if a function has no elementary antiderivative (for instance, exp(-x2)), its definite integral can be approximated using numerical integrationNumerical integrationIn numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...
- to calculate the (
 times) repeated antiderivative of a function
times) repeated antiderivative of a function  Cauchy's formula is useful (cf. Cauchy formula for repeated integrationCauchy formula for repeated integrationThe Cauchy formula for repeated integration, named after Augustin Louis Cauchy, allows one to compress n antidifferentiations of a function into a single integral .-Scalar case:Let ƒ be a continuous function on the real line...
Cauchy's formula is useful (cf. Cauchy formula for repeated integrationCauchy formula for repeated integrationThe Cauchy formula for repeated integration, named after Augustin Louis Cauchy, allows one to compress n antidifferentiations of a function into a single integral .-Scalar case:Let ƒ be a continuous function on the real line...
):
Antiderivatives of non-continuous functions
Non-continuous functions can have antiderivatives. While there are still open questions in this area, it is known that:- Some highly pathological functionsPathological (mathematics)In mathematics, a pathological phenomenon is one whose properties are considered atypically bad or counterintuitive; the opposite is well-behaved....
with large sets of discontinuities may nevertheless have antiderivatives. - In some cases, the antiderivatives of such pathological functions may be found by Riemann integrationRiemann integralIn the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
, while in other cases these functions are not Riemann integrable.
Assuming that the domains of the functions are open intervals:
- A necessary, but not sufficient, condition for a function f to have an antiderivative is that f have the intermediate value propertyIntermediate value theoremIn mathematical analysis, the intermediate value theorem states that for each value between the least upper bound and greatest lower bound of the image of a continuous function there is at least one point in its domain that the function maps to that value....
. That is, if [a, b] is a subinterval of the domain of f and d is any real number between f(a) and f(b), then f(c) = d for some c between a and b. To see this, let F be an antiderivative of f and consider the continuous function g(x) = F(x) − dx on the closed interval [a, b]. Then g must have either a maximum or minimum c in the open interval (a, b) and so 0 = g′(c) = f(c) − d. - The set of discontinuities of f must be a meagre set. This set must also be an F-sigma set (since the set of discontinuities of any function must be of this type). Moreover for any meagre F-sigma set, one can construct some function f having an antiderivative, which has the given set as its set of discontinuities.
- If f has an antiderivative, is boundedBounded functionIn mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
on closed finite subintervals of the domain and has a set of discontinuities of Lebesgue measureLebesgue measureIn measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
0, then an antiderivative may be found by integration. - If f has an antiderivative F on a closed interval [a,b], then for any choice of partition
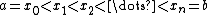 , if one chooses sample points
, if one chooses sample points 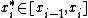 as specified by the mean value theoremMean value theoremIn calculus, the mean value theorem states, roughly, that given an arc of a differentiable curve, there is at least one point on that arc at which the derivative of the curve is equal to the "average" derivative of the arc. Briefly, a suitable infinitesimal element of the arc is parallel to the...
as specified by the mean value theoremMean value theoremIn calculus, the mean value theorem states, roughly, that given an arc of a differentiable curve, there is at least one point on that arc at which the derivative of the curve is equal to the "average" derivative of the arc. Briefly, a suitable infinitesimal element of the arc is parallel to the...
, then the corresponding Riemann sum telescopes to the value F(b) − F(a).
-
-
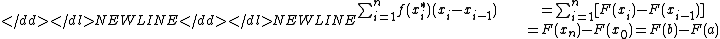
- However if f is unbounded, or if f is bounded but the set of discontinuities of f has positive Lebesgue measure, a different choice of sample points
 may give a significantly different value for the Riemann sum, no matter how fine the partition. See Example 4 below.
may give a significantly different value for the Riemann sum, no matter how fine the partition. See Example 4 below.
Some examples
- The function

with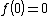 is not continuous at
is not continuous at  but has the antiderivative
but has the antiderivative

with . Since f is bounded on closed finite intervals and is only discontinuous at 0, the antiderivative F may be obtained by integration:
. Since f is bounded on closed finite intervals and is only discontinuous at 0, the antiderivative F may be obtained by integration:  .
.
- The function

with is not continuous at
is not continuous at  but has the antiderivative
but has the antiderivative

with . Unlike Example 1, f(x) is unbounded in any interval containing 0, so the Riemann integral is undefined.
. Unlike Example 1, f(x) is unbounded in any interval containing 0, so the Riemann integral is undefined.
- If f(x) is the function in Example 1 and F is its antiderivative, and
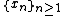 is a denseDense setIn topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
is a denseDense setIn topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
countable subset of the open interval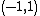 , then the function
, then the function

has an antiderivative
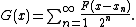
The set of discontinuities of g is precisely the set . Since g is bounded on closed finite intervals and the set of discontinuities has measure 0, the antiderivative G may be found by integration.
. Since g is bounded on closed finite intervals and the set of discontinuities has measure 0, the antiderivative G may be found by integration.
- Let
 be a denseDense setIn topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
be a denseDense setIn topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
countable subset of the open interval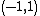 . Consider the everywhere continuous strictly increasing function
. Consider the everywhere continuous strictly increasing function
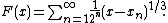
It can be shown that

 for all values x where the series converges, and that the graph of F(x) has vertical tangent lines at all other values of x. In particular the graph has vertical tangent lines at all points in the set
for all values x where the series converges, and that the graph of F(x) has vertical tangent lines at all other values of x. In particular the graph has vertical tangent lines at all points in the set
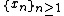 .
.
Moreover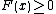 for all x where the derivative is defined. It follows that the inverse function
for all x where the derivative is defined. It follows that the inverse function  is differentiable everywhere and that
is differentiable everywhere and that

for all x in the set which is dense in the interval
which is dense in the interval 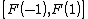 . Thus g has an antiderivative G. On the other hand, it can not be true that
. Thus g has an antiderivative G. On the other hand, it can not be true that

since for any partition of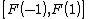 , one can choose sample points for the Riemann sum from the set
, one can choose sample points for the Riemann sum from the set 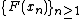 , giving a value of 0 for the sum. It follows that g has a set of discontinuities of positive Lebesgue measure. Figure 1 on the right shows an approximation to the graph of g(x) where
, giving a value of 0 for the sum. It follows that g has a set of discontinuities of positive Lebesgue measure. Figure 1 on the right shows an approximation to the graph of g(x) where  and the series is truncated to 8 terms. Figure 2 shows the graph of an approximation to the antiderivative G(x), also truncated to 8 terms. On the other hand if the Riemann integral is replaced by the Lebesgue integral, then Fatou's lemmaFatou's lemmaIn mathematics, Fatou's lemma establishes an inequality relating the integral of the limit inferior of a sequence of functions to the limit inferior of integrals of these functions...
and the series is truncated to 8 terms. Figure 2 shows the graph of an approximation to the antiderivative G(x), also truncated to 8 terms. On the other hand if the Riemann integral is replaced by the Lebesgue integral, then Fatou's lemmaFatou's lemmaIn mathematics, Fatou's lemma establishes an inequality relating the integral of the limit inferior of a sequence of functions to the limit inferior of integrals of these functions...
or the dominated convergence theoremDominated convergence theoremIn measure theory, Lebesgue's dominated convergence theorem provides sufficient conditions under which two limit processes commute, namely Lebesgue integration and almost everywhere convergence of a sequence of functions...
shows that g does satisfy the fundamental theorem of calculus in that context.
- In Examples 3 and 4, the sets of discontinuities of the functions g are dense only in a finite open interval
 . However these examples can be easily modified so as to have sets of discontinuities which are dense on the entire real line
. However these examples can be easily modified so as to have sets of discontinuities which are dense on the entire real line  . Let
. Let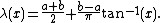
Then has a dense set of discontinuities on
has a dense set of discontinuities on 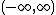 and has antiderivative
and has antiderivative 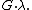
- Using a similar method as in Example 5, one can modify g in Example 4 so as to vanish at all rational numbers. If one uses a naive version of the Riemann integralRiemann integralIn the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
defined as the limit of left-hand or right-hand Riemann sums over regular partitions, one will obtain that the integral of such a function g over an interval is 0 whenever a and b are both rational, instead of
is 0 whenever a and b are both rational, instead of 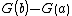 . Thus the fundamental theorem of calculus will fail spectacularly.
. Thus the fundamental theorem of calculus will fail spectacularly.
See also
- Antiderivative (complex analysis)Antiderivative (complex analysis)In complex analysis, a branch of mathematics, the antiderivative, or primitive, of a complex-valued function g is a function whose complex derivative is g...
- Lists of integrals
- Symbolic integrationSymbolic integrationIn calculus symbolic integration is the problem of finding a formula for the antiderivative, or indefinite integral, of a given function f, i.e...
External links
- Wolfram Integrator — Free online symbolic integration with MathematicaMathematicaMathematica is a computational software program used in scientific, engineering, and mathematical fields and other areas of technical computing...
- Mathematical Assistant on Web — symbolic computations online. Allows to integrate in small steps (with hints for next step (integration by parts, substitution, partial fractions, application of formulas and others), powered by Maxima
- Function Calculator from WIMS
- Integral
- "The Indefinite Integral or Anti-derivative " at the Khan AcademyKhan AcademyThe Khan Academy is a not-for-profit educational organization, created in 2006 by Bangladeshi American educator Salman Khan, a graduate of MIT. With the stated mission of "providing a high quality education to anyone, anywhere", the website supplies a free online collection of more than 2,700 micro...
- However if f is unbounded, or if f is bounded but the set of discontinuities of f has positive Lebesgue measure, a different choice of sample points
-


