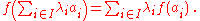Affine transformation
Encyclopedia

Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, an affine transformation or affine map or an affinity (from the Latin, affinis, "connected with") is a transformation which preserves straight lines. It is the most general class of transformations with this property. It is equivalent to a translation
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
followed by a linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
.
Mathematical Definition
An affine map between two affine space
between two affine spaceAffine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
s is a map that acts on vectors, defined by pairs of points, as a linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
: there exists a linear transformation φ such that

for any pair of points
 . If an origin
. If an origin 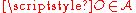 is chosen, and
is chosen, and  denotes its image
denotes its image 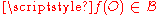 , then this means that for any vector
, then this means that for any vector  :
:
If an origin
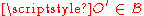 is also chosen, this can be decomposed as an affine transformation
is also chosen, this can be decomposed as an affine transformation  that sends
that sends  , namely
, namely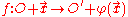
followed by the translation by a vector
 .
.The conclusion is that, heuristically,
 consists of a translation and a linear map.
consists of a translation and a linear map.Another definition is: Given two affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
s
 and
and  , over the same field, a function
, over the same field, a function  is an affine map if and only if for every family
is an affine map if and only if for every family 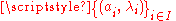 of weighted points in
of weighted points in  such that
such that  we have
we haveIn other words,
 preserves barycenters.
preserves barycenters.In the finite-dimensional case, an affine map can be specified in coordinates by a matrix A (describing φ) together with the vector
 .
.An affine transformation preserves
- The collinearityLine (geometry)The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
relation between points; i.e., the points which lie on a line continue to be collinear after the transformation - Ratios of vectors along a line; i.e., for distinct collinear points
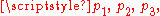 the ratio of
the ratio of  and
and  is the same as that of
is the same as that of  and
and  .
. - More generally barycenters of weighted collections of points.
Representation
Ordinary vector algebra uses matrix multiplication to represent linear transformations, and vector addition to represent translations. Using an augmented matrixAugmented matrix
In linear algebra, an augmented matrix is a matrix obtained by appending the columns of two given matrices, usually for the purpose of performing the same elementary row operations on each of the given matrices.Given the matrices A and B, where:A =...
and an augmented vector, it is possible to represent both using a single matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
. The technique requires that all vectors are augmented with a "1" at the end, and all matrices are augmented with an extra row of zeros at the bottom, an extra column—the translation vector—to the right, and a "1" in the lower right corner. If A is a matrix,
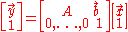
is equivalent to the following
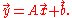
The above mentioned augmented matrix is called affine transformation matrix, or projective transformation matrix (as it can also be used to perform Projective transformations).
This representation exhibits the set of all invertible
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
affine transformations as the semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of Kn and GL(n, k). This is a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
under the operation of composition of functions, called the affine group
Affine group
In mathematics, the affine group or general affine group of any affine space over a field K is the group of all invertible affine transformations from the space into itself.It is a Lie group if K is the real or complex field or quaternions....
.
Ordinary matrix-vector multiplication always maps the origin to the origin, and could therefore never represent a translation, in which the origin must necessarily be mapped to some other point. By appending the additional coordinate "1" to every vector, one essentially considers the space to be mapped as a subset of a space with an additional dimension. In that space, the original space occupies the subset in which the additional coordinate is 1. Thus the origin of the original space can be found at (0,0, ... 0, 1). A translation within the original space by means of a linear transformation of the higher-dimensional space is then possible (specifically, a shear transformation). The coordinates in the higher-dimensional space are an example of homogeneous coordinates
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
. If the original space is Euclidean
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, the higher dimensional space is a real projective space
Real projective space
In mathematics, real projective space, or RPn, is the topological space of lines through 0 in Rn+1. It is a compact, smooth manifold of dimension n, and a special case of a Grassmannian.-Construction:...
.
The advantage of using homogeneous coordinates is that one can combine
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
any number of affine transformations into one by multiplying the respective matrices. This property is used extensively in computer graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
.
Properties
An affine transformation is invertible if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
A is invertible. In the matrix representation, the inverse is:
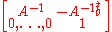
The invertible affine transformations (of an affine space onto itself) form the affine group
Affine group
In mathematics, the affine group or general affine group of any affine space over a field K is the group of all invertible affine transformations from the space into itself.It is a Lie group if K is the real or complex field or quaternions....
, which has the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
of degree n as subgroup and is itself a subgroup of the general linear group of degree n + 1.
The similarity transformations form the subgroup where A is a scalar times an orthogonal matrix
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
. If and only if the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of A is 1 or −1 then the transformation preserves area; these also form a subgroup. Combining both conditions we have the isometries
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
, the subgroup of both where A is an orthogonal matrix.
Each of these groups has a subgroup of transformations which preserve orientation
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
: those where the determinant of A is positive. In the last case this is in 3D the group of rigid body
Rigid body
In physics, a rigid body is an idealization of a solid body of finite size in which deformation is neglected. In other words, the distance between any two given points of a rigid body remains constant in time regardless of external forces exerted on it...
motions (proper rotation
Improper rotation
In 3D geometry, an improper rotation, also called rotoreflection or rotary reflection is, depending on context, a linear transformation or affine transformation which is the combination of a rotation about an axis and a reflection in a plane perpendicular to the axis.Equivalently it is the...
s and pure translations).
For any matrix A the following propositions are equivalent:
- A − I is invertible
- A does not have an eigenvalue equal to 1
- for all b the transformation has exactly one fixed pointFixed point (mathematics)In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
- there is a b for which the transformation has exactly one fixed point
- affine transformations with matrix A can be written as a linear transformation with some point as origin
If there is a fixed point, we can take that as the origin, and the affine transformation reduces to a linear transformation. This may make it easier to classify and understand the transformation. For example, describing a transformation as a rotation by a certain angle with respect to a certain axis is easier to get an idea of the overall behavior of the transformation than describing it as a combination of a translation and a rotation. However, this depends on application and context. Describing such a transformation for an object tends to make more sense in terms of rotation about an axis through the center of that object, combined with a translation, rather than by just a rotation with respect to some distant point. As an example: "move 200 m north and rotate 90° anti-clockwise", rather than the equivalent "with respect to the point 141 m to the northwest, rotate 90° anti-clockwise".
Affine transformations in 2D without fixed point (so where A has eigenvalue 1) are:
- pure translations
- scalingScaling (geometry)In Euclidean geometry, uniform scaling is a linear transformation that enlarges or shrinks objects by a scale factor that is the same in all directions. The result of uniform scaling is similar to the original...
in a given direction, with respect to a line in another direction (not necessarily perpendicular), combined with translation that is not purely in the direction of scaling; the scale factorScale factorA scale factor is a number which scales, or multiplies, some quantity. In the equation y=Cx, C is the scale factor for x. C is also the coefficient of x, and may be called the constant of proportionality of y to x...
is the other eigenvalue; taking "scaling" in a generalized sense it includes the cases that the scale factor is zero (projectionProjection (linear algebra)In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself such that P2 = P. It leaves its image unchanged....
) and negative; the latter includes reflectionReflection (mathematics)In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
, and combined with translation it includes glide reflectionGlide reflectionIn geometry, a glide reflection is a type of isometry of the Euclidean plane: the combination of a reflection in a line and a translation along that line. Reversing the order of combining gives the same result...
. - shearShear (mathematics)In mathematics, shear mapping or transvection is a particular kind of linear mapping. Linear mapping is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication...
combined with translation that is not purely in the direction of the shear (there is no other eigenvalue than 1; it has algebraic multiplicity 2, but geometric multiplicity 1)
Affine transformation of the plane
To visualise the general affine transformation of the Euclidean plane, take labelled parallelogramParallelogram
In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...
s ABCD and A′B′C′D′. Whatever the choices of points, there is an affine transformation T of the plane taking A to A′, and each vertex similarly. Supposing we exclude the degenerate case where ABCD has zero area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
, there is a unique such affine transformation T. Drawing out a whole grid of parallelograms based on ABCD, the image T(P) of any point P is determined by noting that T(A) = A′, T applied to the line segment AB is A′B′, T applied to the line segment AC is A′C′, and T respects scalar multiples of vectors based at A. [If A, E, F are collinear then the ratio length(AF)/length(AE) is equal to length(A′F′)/length(A′E′).] Geometrically T transforms the grid based on ABCD to that based in A′B′C′D′.
Affine transformations don't respect lengths or angles; they multiply area by a constant factor
- area of A′B′C′D′ / area of ABCD.
A given T may either be direct (respect orientation), or indirect (reverse orientation), and this may be determined by its effect on signed areas (as defined, for example, by the cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
of vectors).
Affine transformation over a finite field
The following equation expresses an affine transformation in GF(28) (with "+" representing XOR):
where [M] is the matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...

and {v} is the vector
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
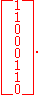
For instance, the affine transformation of the element {a} = y7 + y6 + y3 + y = {11001010} in big-endian
Endianness
In computing, the term endian or endianness refers to the ordering of individually addressable sub-components within the representation of a larger data item as stored in external memory . Each sub-component in the representation has a unique degree of significance, like the place value of digits...
binary
Binary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
notation = {CA} in big-endian hexadecimal
Hexadecimal
In mathematics and computer science, hexadecimal is a positional numeral system with a radix, or base, of 16. It uses sixteen distinct symbols, most often the symbols 0–9 to represent values zero to nine, and A, B, C, D, E, F to represent values ten to fifteen...
notation, is calculated as follows:




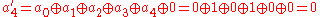

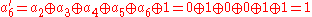

Thus, {a′} = y7 + y6 + y5 + y3 + y2 + 1 = {11101101} = {ED}.
Affine transformation in plane geometry
In ℝ2, the transformation shown at right is accomplished using the map given by: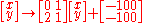
Transforming the three corner points of the original triangle (in red) gives three new points which form the new triangle (in blue). This transformation skews and translates the original triangle.
In fact, all triangles are related to one another by affine transformations. This is also true for all parallelograms, but not for all quadrilaterals.
See also
- The transformation matrix for an affine transformation
- Affine geometryAffine geometryIn mathematics affine geometry is the study of geometric properties which remain unchanged by affine transformations, i.e. non-singular linear transformations and translations...
- Homothetic transformation
- Similarity transformation
- Linear transformationLinear transformationIn mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
(the second meaning is affine transformation in 1D) - 3D projection3D projection3D projection is any method of mapping three-dimensional points to a two-dimensional plane. As most current methods for displaying graphical data are based on planar two-dimensional media, the use of this type of projection is widespread, especially in computer graphics, engineering and drafting.-...
- Flat (geometry)Flat (geometry)In geometry, a flat is a subset of n-dimensional space that is congruent to a Euclidean space of lower dimension. The flats in two-dimensional space are points and lines, and the flats in three-dimensional space are points, lines, and planes....
External links
- Geometric Operations: Affine Transform, R. Fisher, S. Perkins, A. Walker and E. Wolfart.
- Affine Transform by Bernard Vuilleumier, Wolfram Demonstrations ProjectWolfram Demonstrations ProjectThe Wolfram Demonstrations Project is hosted by Wolfram Research, whose stated goal is to bring computational exploration to the widest possible audience. It consists of an organized, open-source collection of small interactive programs called Demonstrations, which are meant to visually and...
. - Affine Transformation on PlanetMath
- Free Affine Transformation software