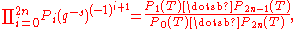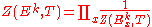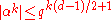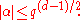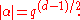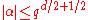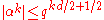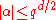Weil conjectures
Encyclopedia
In mathematics
, the Weil conjectures were some highly-influential proposals by on the generating function
s (known as local zeta-function
s) derived from counting the number of points on algebraic varieties
over finite field
s.
A variety V over a finite field with q elements has a finite number of rational points, as well as points over every finite field with qk elements containing that field. The generating function has coefficients derived from the numbers Nk of points over the (essentially unique) field with qk elements.
Weil conjectured that such zeta-functions should be rational function
s, should satisfy a form of functional equation
, and should have their zeroes in restricted places. The last two parts were quite consciously modeled on the Riemann zeta function and Riemann hypothesis
.
The rationality was proved by , the functional equation by , and the analogue of the Riemann hypothesis was proved by
and appears in section VII of his Disquisitiones Arithmeticae
, concerned with roots of unity and Gaussian period
s. In article 358, he moves on from the periods that build up towers of quadratic extensions, for the construction of regular polygons; and assumes that p is a prime number such that is divisible by 3. Then there is a cyclic cubic field inside the cyclotomic field of pth roots of unity, and a normal integral basis of periods for the integers of this field (an instance of the Hilbert–Speiser theorem). Gauss constructs the order-3 periods, corresponding to the cyclic group
(Z/pZ)× of non-zero residues modulo p under multiplication and its unique subgroup of index three. Gauss lets
, 
, and 
be its cosets. Taking the periods (sums of roots of unity) corresponding to these cosets applied to exp(2πi/p), he notes that these periods have a multiplication table that is accessible to calculation. Products are linear combinations of the periods, and he determines the coefficients. He sets, for example,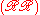 
equal to the number of elements of Z/pZ which are in 
and which, after being increased by one, are also in 
. He proves that this number and related ones are the coefficients of the products of the periods. To see the relation of these sets to the Weil conjectures, notice that if α and are both in 
, then there exist x and y in Z/pZ such that x3 = α and y3 = α + 1; consequently, x3 + 1 = y3. Therefore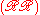 
is the number of solutions to x3 + 1 = y3 in the finite field Z/pZ. The other coefficients have similar interpretations. Gauss's determination of the coefficients of the products of the periods therefore counts the number of points on these elliptic curve
s, and as a byproduct he proves the analog of the Riemann hypothesis.
The Weil conjectures in the special case of algebraic curve
s were conjectured by . The case of curves over finite fields was proved by Weil, finishing the project started by Hasse's theorem on elliptic curves over finite fields. Their interest was obvious enough from within number theory
: they implied upper bounds for exponential sum
s, a basic concern in analytic number theory
.
What was really eye-catching, from the point of view of other mathematical areas, was the proposed connection with algebraic topology
. Given that finite fields are discrete in nature, and topology speaks only about the continuous, the detailed formulation of Weil (based on working out some examples) was striking and novel. It suggested that geometry over finite fields should fit into well-known patterns relating to Betti number
s, the Lefschetz fixed-point theorem
and so on.
The analogy with topology suggested that a new homological theory be set up applying within algebraic geometry
. This took two decades (it was a central aim of the work and school of Alexander Grothendieck
) building up on initial suggestions from Serre
. The rationality part of the conjectures was proved first by , using p-adic
methods. and his collaborators established the rationality conjecture, the functional equation and the link to Betti numbers by using the properties of étale cohomology
, a new cohomology theory developed by Grothendieck and Artin for attacking the Weil conjectures, as outlined in .
Of the four conjectures the analogue of the Riemann hypothesis was the hardest to prove. Motivated by the proof of of an analogue of the Weil conjectures for Kähler manifold
s, Grothendieck envisioned a proof based on his standard conjectures on algebraic cycles
. However, the standard conjectures remain open (except for the hard Lefschetz theorem, which was proved by Deligne by extending his work on the Weil conjectures), and the analogue of the Riemann hypothesis was proved by , using the étale cohomology theory but circumventing the use of standard conjectures by an ingenious argument.
found and proved a generalization of the Weil conjectures, bounding the weights of the pushforward of a sheaf.
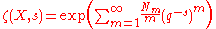
where Nm is the number of points of X defined over the degree m extension Fqm of Fq.
The Weil conjectures state:
of T = q−s. More precisely, ζ(X, s) can be written as a finite alternating product
for some numbers αij.
(Functional equation and Poincaré duality) The zeta function satisfies E is the Euler characteristic
of X. In particular, for each i, the numbers α2n-i,1, α2n-i,2, … equal the numbers qn/αi,1, qn/αi,2, … in some order.(Riemann hypothesis) |α i,j| = qi/2 for all and all j. This implies that all zeros of Pk(T) lie on the "critical line" of complex numbers s with real part k/2.
(Betti numbers) If X is a (good) "reduction mod p" of a non-singular projective variety Y defined over a number field embedded in the field of complex numbers, then the degree of Pi is the ith Betti number
of the space of complex points of Y.
It is easy to check all parts of the Weil conjectures directly. For example, the corresponding complex variety is the Riemann sphere
and its initial Betti numbers are 1, 0, 1.
The number of points of X over a field with qm elements is
just Nm = 1 + qm + q2m + ... + qnm. The zeta function is just
It is again easy to check all parts of the Weil conjectures directly. (Complex projective space
gives the relevant Betti numbers, which nearly determine the answer.)
The reason why the projective line and projective space were so easy is that they can be written as disjoint unions of a finite number of copies of affine spaces, which makes the number of points on them particularly easy to calculate. It is also easy to prove the Weil conjectures for other spaces, such as Grassmannians, that have the same property.
If E is an elliptic curve over a finite field with q elements, then the number of points of E defined over the field with qm elements is 1 − αm− βm + qm,
where α and β are complex conjugates with absolute value √q.
The zeta function is
" for varieties over finite fields, similar to the usual cohomology with rational coefficients for complex varieties.
His idea was that if F is the Frobenius automorphism over the finite field, then the number of points of the variety X over the field of order qm is the number of fixed points of Fm (acting on all points of the variety X defined over the algebraic closure). In algebraic topology the number of fixed points of an automorphism can be worked out using the Lefschetz fixed point theorem, given as an alternating sum of traces on the cohomology groups. So if there were similar cohomology groups for varieties over finite fields, then the zeta function could be expressed in terms of them.
The first problem with this is that the coefficient field for a Weil cohomology theory cannot be the rational numbers. To see this consider the case of a supersingular elliptic curve
over a finite field of characteristic p. The endomorphism ring of this is an order in a quaternion algebra
over the rationals, and should act on the first cohomology group, which should be a 2 dimensional vector space over the coefficient field by analogy with the case of a complex elliptic curve. However a quaternion algebra over the rationals cannot act on a 2 dimensional vector space over the rationals. The same argument eliminates the possibility of the coefficient field being the reals or the p-adic numbers, because the quaternion algebra is still a division algebra over these fields. However it does not eliminate the possibility that the coefficient field is the field of l-adic numbers for some prime l ≠ p, because over these fields the division algebra splits and becomes a matrix algebra, which can act on a 2-dimensional vector space. Grothendieck and Michael Artin
managed to construct suitable cohomology theories over the field of l-adic numbers for each prime l ≠ p, called l-adic cohomology.
where each polynomial Pi is the determinant of I − TF on the l-adic cohomology group Hi.
The rationality of the zeta function follows immediately. The functional equation for the zeta function follows from Poincaré duality for l-adic cohomology, and the relation with complex Betti numbers of a lift follows from a comparison theorem between l-adic and ordinary cohomology for complex varieties.
More generally, Grothendieck proved a similar formula for the zeta function of a sheaf F0:
as a product over cohomology groups:
The special case of the constant sheaf gives the usual zeta function.
Deligne's first proof of the Weil conjectures used the following steps:
After blowing up
V and extending the base field, one may assume that the variety V has a morphism onto the projective line P1, with a finite number of singular fibers with very mild (quadratic) singularities. The theory of monodromy of Lefschetz pencil
s, introduced for complex varieties (and ordinary cohomology) by , and extended by and to l-adic cohomology, relates the cohomology of V to that of its fibers. The relation depends on the space Ex of vanishing cycles, the subspace of the cohomology Hd−1(Vx) of a non-singular fiber Vx, spanned by classes that vanish on singular fibers.
The Leray spectral sequence
relates the middle cohomology group of V to the cohomology of the fiber and base. The hard part to deal with is more or less a group H1(P1, j*E) = H(U,E), where U is the points the projective line with non-singular fibers, and j is the inclusion of U into the projective line, and E is the sheaf with fibers the spaces Ex of vanishing cycles.
If k is even then all the coefficients of the factors on the right (considered as power series in T) are non-negative; this follows by writing
and using the fact that the traces of powers of F are rational, so their k powers are non-negative as k is even. Deligne proves the rationality of the traces by relating them to numbers of points of varieties, which are always (rational) integers.
This estimate can be used to find the absolute value of any eigenvalue α of Frobenius on a fiber of E as follows. For any integer k, αk is an eigenvalue of Frobenius on a stalk of Ek, which for k even is bounded by q1+k(d−1)/2. So
As this is true for arbitrarily large even k, this implies that
Poincaré duality
then implies that
A constructible sheaf on a variety over a finite field is called pure of weight β if for all points x the eigenvalues of the Frobenius at x all have absolute value N(x)β/2, and is called mixed of weight ≤β if it can be written as repeated extensions by pure sheaves with weights ≤β.
Deligne's theorem states that if f is a morphism of schemes of finite type over a finite field, then Rif! takes mixed sheaves of weight ≤β to mixed sheaves of weight ≤β+i.
The original Weil conjectures follow by taking f to be a morphism from a smooth projective variety to a point and considering the constant sheaf Ql on the variety. This gives an upper bound on the absolute values of the eigenvalues of Frobenius, and Poincaré duality then shows that this is also a lower bound.
In general Rif! does not take pure sheaves to pure sheaves. However it does when a suitable form of Poincaré duality holds, for example if f is smooth and proper, or if one works with perverse sheaves rather than sheaves as in .
Inspired by the work of on Morse theory
, found another proof, using Deligne's l-adic Fourier transform
, which allowed him to simplify Deligne's proof by avoiding the use of the method of Hadamard and de la Vallée Poussin. His proof generalizes the classical calculation of the absolute value of Gauss sum
s using the fact that the norm of a Fourier transform has a simple relation to the norm of the original function. used Laumon's proof as the basis for their exposition of Deligne's theorem. gave a further simplification of Laumon's proof, using monodromy in the spirit of Deligne's first proof. gave another proof using the Fourier transform, replacing etale cohomology with rigid cohomology
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Weil conjectures were some highly-influential proposals by on the generating function
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
s (known as local zeta-function
Local zeta-function
In number theory, a local zeta-functionis a function whose logarithmic derivative is a generating functionfor the number of solutions of a set of equations defined over a finite field F, in extension fields Fk of F.-Formulation:...
s) derived from counting the number of points on algebraic varieties
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
over finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s.
A variety V over a finite field with q elements has a finite number of rational points, as well as points over every finite field with qk elements containing that field. The generating function has coefficients derived from the numbers Nk of points over the (essentially unique) field with qk elements.
Weil conjectured that such zeta-functions should be rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s, should satisfy a form of functional equation
Functional equation
In mathematics, a functional equation is any equation that specifies a function in implicit form.Often, the equation relates the value of a function at some point with its values at other points. For instance, properties of functions can be determined by considering the types of functional...
, and should have their zeroes in restricted places. The last two parts were quite consciously modeled on the Riemann zeta function and Riemann hypothesis
Riemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
.
The rationality was proved by , the functional equation by , and the analogue of the Riemann hypothesis was proved by
Background and history
The earliest antecedent of the Weil conjectures is by Carl Friedrich GaussCarl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
and appears in section VII of his Disquisitiones Arithmeticae
Disquisitiones Arithmeticae
The Disquisitiones Arithmeticae is a textbook of number theory written in Latin by Carl Friedrich Gauss in 1798 when Gauss was 21 and first published in 1801 when he was 24...
, concerned with roots of unity and Gaussian period
Gaussian period
In mathematics, in the area of number theory, a Gaussian period is a certain kind of sum of roots of unity. The periods permit explicit calculations in cyclotomic fields connected with Galois theory and with harmonic analysis . They are basic in the classical theory called cyclotomy...
s. In article 358, he moves on from the periods that build up towers of quadratic extensions, for the construction of regular polygons; and assumes that p is a prime number such that is divisible by 3. Then there is a cyclic cubic field inside the cyclotomic field of pth roots of unity, and a normal integral basis of periods for the integers of this field (an instance of the Hilbert–Speiser theorem). Gauss constructs the order-3 periods, corresponding to the cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
(Z/pZ)× of non-zero residues modulo p under multiplication and its unique subgroup of index three. Gauss lets
, , and be its cosets. Taking the periods (sums of roots of unity) corresponding to these cosets applied to exp(2πi/p), he notes that these periods have a multiplication table that is accessible to calculation. Products are linear combinations of the periods, and he determines the coefficients. He sets, for example, 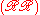equal to the number of elements of Z/pZ which are in and which, after being increased by one, are also in . He proves that this number and related ones are the coefficients of the products of the periods. To see the relation of these sets to the Weil conjectures, notice that if α and are both in , then there exist x and y in Z/pZ such that x3 = α and y3 = α + 1; consequently, x3 + 1 = y3. Therefore 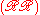is the number of solutions to x3 + 1 = y3 in the finite field Z/pZ. The other coefficients have similar interpretations. Gauss's determination of the coefficients of the products of the periods therefore counts the number of points on these elliptic curveElliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s, and as a byproduct he proves the analog of the Riemann hypothesis.
The Weil conjectures in the special case of algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
s were conjectured by . The case of curves over finite fields was proved by Weil, finishing the project started by Hasse's theorem on elliptic curves over finite fields. Their interest was obvious enough from within number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
: they implied upper bounds for exponential sum
Exponential sum
In mathematics, an exponential sum may be a finite Fourier series , or other finite sum formed using the exponential function, usually expressed by means of the functione = \exp.\,...
s, a basic concern in analytic number theory
Analytic number theory
In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Dirichlet's introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic...
.
What was really eye-catching, from the point of view of other mathematical areas, was the proposed connection with algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
. Given that finite fields are discrete in nature, and topology speaks only about the continuous, the detailed formulation of Weil (based on working out some examples) was striking and novel. It suggested that geometry over finite fields should fit into well-known patterns relating to Betti number
Betti number
In algebraic topology, a mathematical discipline, the Betti numbers can be used to distinguish topological spaces. Intuitively, the first Betti number of a space counts the maximum number of cuts that can be made without dividing the space into two pieces....
s, the Lefschetz fixed-point theorem
Lefschetz fixed-point theorem
In mathematics, the Lefschetz fixed-point theorem is a formula that counts the fixed points of a continuous mapping from a compact topological space X to itself by means of traces of the induced mappings on the homology groups of X...
and so on.
The analogy with topology suggested that a new homological theory be set up applying within algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
. This took two decades (it was a central aim of the work and school of Alexander Grothendieck
Alexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
) building up on initial suggestions from Serre
Jean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
. The rationality part of the conjectures was proved first by , using p-adic
P-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
methods. and his collaborators established the rationality conjecture, the functional equation and the link to Betti numbers by using the properties of étale cohomology
Étale cohomology
In mathematics, the étale cohomology groups of an algebraic variety or scheme are algebraic analogues of the usual cohomology groups with finite coefficients of a topological space, introduced by Grothendieck in order to prove the Weil conjectures...
, a new cohomology theory developed by Grothendieck and Artin for attacking the Weil conjectures, as outlined in .
Of the four conjectures the analogue of the Riemann hypothesis was the hardest to prove. Motivated by the proof of of an analogue of the Weil conjectures for Kähler manifold
Kähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
s, Grothendieck envisioned a proof based on his standard conjectures on algebraic cycles
Standard conjectures on algebraic cycles
In mathematics, the standard conjectures about algebraic cycles is a package of several conjectures describing the relationship of algebraic cycles and Weil cohomology theories. One of the original applications of these conjectures, envisaged by Alexander Grothendieck, was to prove that his...
. However, the standard conjectures remain open (except for the hard Lefschetz theorem, which was proved by Deligne by extending his work on the Weil conjectures), and the analogue of the Riemann hypothesis was proved by , using the étale cohomology theory but circumventing the use of standard conjectures by an ingenious argument.
found and proved a generalization of the Weil conjectures, bounding the weights of the pushforward of a sheaf.
Statement of the Weil conjectures
Suppose that X is a non-singular n-dimensional projective algebraic variety over the field Fq with q elements. The zeta function ζ(X, s) of X is by definition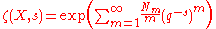where Nm is the number of points of X defined over the degree m extension Fqm of Fq.
The Weil conjectures state:
- (Rationality) ζ(
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
of T = q−s. More precisely, ζ(X, s) can be written as a finite alternating product
for some numbers αij.
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
of X. In particular, for each i, the numbers α2n-i,1, α2n-i,2, … equal the numbers qn/αi,1, qn/αi,2, … in some order.
Betti number
In algebraic topology, a mathematical discipline, the Betti numbers can be used to distinguish topological spaces. Intuitively, the first Betti number of a space counts the maximum number of cuts that can be made without dividing the space into two pieces....
of the space of complex points of Y.
The projective line
The simplest example (other than a point) is to take X to be the projective line. The number of points of X over a field with qm elements is just Nm = qm + 1 (where the "+ 1" comes from the "point at infinity"). The zeta function is just- 1/(1 −
It is easy to check all parts of the Weil conjectures directly. For example, the corresponding complex variety is the Riemann sphere
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
and its initial Betti numbers are 1, 0, 1.
Projective space
It is not much harder to do n dimensional projective space.The number of points of X over a field with qm elements is
just Nm = 1 + qm + q2m + ... + qnm. The zeta function is just
- 1/(1 −
It is again easy to check all parts of the Weil conjectures directly. (Complex projective space
Complex projective space
In mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines...
gives the relevant Betti numbers, which nearly determine the answer.)
The reason why the projective line and projective space were so easy is that they can be written as disjoint unions of a finite number of copies of affine spaces, which makes the number of points on them particularly easy to calculate. It is also easy to prove the Weil conjectures for other spaces, such as Grassmannians, that have the same property.
Elliptic curves
These give the first non-trivial cases of the Weil conjectures (proved by Hasse).If E is an elliptic curve over a finite field with q elements, then the number of points of E defined over the field with qm elements is 1 − αm− βm + qm,
where α and β are complex conjugates with absolute value √q.
The zeta function is
- ζ(
Weil cohomology
Weil suggested that the conjectures would follow from the existence of a suitable "Weil cohomology theoryWeil cohomology theory
In algebraic geometry, a Weil cohomology or Weil cohomology theory is a cohomology satisfying certain axioms concerning the interplay of algebraic cycles and cohomology groups. The name is in honor of André Weil...
" for varieties over finite fields, similar to the usual cohomology with rational coefficients for complex varieties.
His idea was that if F is the Frobenius automorphism over the finite field, then the number of points of the variety X over the field of order qm is the number of fixed points of Fm (acting on all points of the variety X defined over the algebraic closure). In algebraic topology the number of fixed points of an automorphism can be worked out using the Lefschetz fixed point theorem, given as an alternating sum of traces on the cohomology groups. So if there were similar cohomology groups for varieties over finite fields, then the zeta function could be expressed in terms of them.
The first problem with this is that the coefficient field for a Weil cohomology theory cannot be the rational numbers. To see this consider the case of a supersingular elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
over a finite field of characteristic p. The endomorphism ring of this is an order in a quaternion algebra
Quaternion algebra
In mathematics, a quaternion algebra over a field F is a central simple algebra A over F that has dimension 4 over F. Every quaternion algebra becomes the matrix algebra by extending scalars , i.e...
over the rationals, and should act on the first cohomology group, which should be a 2 dimensional vector space over the coefficient field by analogy with the case of a complex elliptic curve. However a quaternion algebra over the rationals cannot act on a 2 dimensional vector space over the rationals. The same argument eliminates the possibility of the coefficient field being the reals or the p-adic numbers, because the quaternion algebra is still a division algebra over these fields. However it does not eliminate the possibility that the coefficient field is the field of l-adic numbers for some prime l ≠ p, because over these fields the division algebra splits and becomes a matrix algebra, which can act on a 2-dimensional vector space. Grothendieck and Michael Artin
Michael Artin
Michael Artin is an American mathematician and a professor emeritus in the Massachusetts Institute of Technology mathematics department, known for his contributions to algebraic geometry. and also generally recognized as one of the outstanding professors in his field.Artin was born in Hamburg,...
managed to construct suitable cohomology theories over the field of l-adic numbers for each prime l ≠ p, called l-adic cohomology.
Grothendieck's formula for the zeta function
Grothendieck proved an analogue of the Lefschetz fixed point formula for l-adic cohomology theory, and by applying it to the Frobenius automorphism F was able to prove the following formula for the zeta function.where each polynomial Pi is the determinant of I − TF on the l-adic cohomology group Hi.
The rationality of the zeta function follows immediately. The functional equation for the zeta function follows from Poincaré duality for l-adic cohomology, and the relation with complex Betti numbers of a lift follows from a comparison theorem between l-adic and ordinary cohomology for complex varieties.
More generally, Grothendieck proved a similar formula for the zeta function of a sheaf F0:
as a product over cohomology groups:
The special case of the constant sheaf gives the usual zeta function.
Deligne's first proof
, , and gave expository accounts of the first proof . Much of the background in l-adic cohomology is described in .Deligne's first proof of the Weil conjectures used the following steps:
Use of Lefschetz pencils
- Grothendieck expressed the zeta function in terms of the trace of Frobenius on
Blowing up
In mathematics, blowing up or blowup is a type of geometric transformation which replaces a subspace of a given space with all the directions pointing out of that subspace. For example, the blowup of a point in a plane replaces the point with the projectivized tangent space at that point...
V and extending the base field, one may assume that the variety V has a morphism onto the projective line P1, with a finite number of singular fibers with very mild (quadratic) singularities. The theory of monodromy of Lefschetz pencil
Lefschetz pencil
In mathematics, a Lefschetz pencil is a construction in algebraic geometry considered by Solomon Lefschetz, in order to analyse the algebraic topology of an algebraic variety V. A pencil here is a particular kind of linear system of divisors on V, namely a one-parameter family, parametrised by the...
s, introduced for complex varieties (and ordinary cohomology) by , and extended by and to l-adic cohomology, relates the cohomology of V to that of its fibers. The relation depends on the space Ex of vanishing cycles, the subspace of the cohomology Hd−1(Vx) of a non-singular fiber Vx, spanned by classes that vanish on singular fibers.
Leray spectral sequence
In mathematics, the Leray spectral sequence was a pioneering example in homological algebra, introduced in 1946 by Jean Leray. The formulation was of a spectral sequence, expressing the relationship holding in sheaf cohomology between two topological spaces X and Y, and set up by a continuous...
relates the middle cohomology group of V to the cohomology of the fiber and base. The hard part to deal with is more or less a group H1(P1, j*E) = H(U,E), where U is the points the projective line with non-singular fibers, and j is the inclusion of U into the projective line, and E is the sheaf with fibers the spaces Ex of vanishing cycles.
The key estimate
The heart of Deligne's proof is to show that the sheaf E over U is pure, in other words to find the absolute values of the eigenvalues of Frobenius on its stalks. This is done by studying the zeta functions of the even powers Ek of E and applying Grothendieck's formula for the zeta functions as alternating products over cohomology groups. The crucial idea of considering even k powers of E was inspired by the paper , who used a similar idea with k=2 for bounding the Ramanujan tau function. pointed out that a generalization of Rankin's result for higher even values of k would imply the Ramanujan conjecture, and Deligne realized that in the case of zeta functions of varieties, Grothendieck's theory of zeta functions of sheaves provided an analogue of this generalization.- The poles of the zeta function of Ek are found using Grothendieck's formula
-
- and calculating the cohomology groups in the denominator explicitly. The H term is usually just 1 as U is usually not compact, and the H can be calculated explicitly as follows. Poincaré duality relates H(Ek) to H(Ek), which is in turn the space of covariants of the monodromy group, which is the geometric fundamental group of U acting on the fiber of Ek at a point. The fiber of E has a bilinear form induced by cup productCup productIn mathematics, specifically in algebraic topology, the cup product is a method of adjoining two cocycles of degree p and q to form a composite cocycle of degree p + q. This defines an associative graded commutative product operation in cohomology, turning the cohomology of a space X into a...
, which is antisymmetric if d is even, and makes E into a symplectic space. (This is a little inaccurate: Deligne did later show that E∩E⊥ = 0 by using the hard Lefschetz theorem, this requires the Weil conjectures, and the proof of the Weil conjectures really has to use a slightly more complicated argument with E/E∩E⊥ rather than E.) An argument of Kazhdan and Margulis shows that the image of the monodromy group acting on E is Zariski dense in a symplectic group and therefore has the same invariants, which are well known from classical invariant theory. Keeping track of the action of Frobenius in this calculation shows that its eigenvalues are all qk(d−1)/2+1, so the zeta function of Z(Ek,T) has poles only at T=1/qk(d−1)/2+1.- The Euler product for the zeta function of
- The powers series for
Poincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
then implies that
Completion of the proof
The deduction of the Riemann hypothesis from this estimate is mostly a fairly straightforward use of standard techniques and is done as follows.- The eigenvalues of Frobenius on H(U,E) can now be estimated as they are the zeros of the zeta function of the sheaf E. This zeta function can be written as an Euler product of zeta functions of the stalks of E, and using the estimate for the eigenvalues on these stalks shows that this product converges for |T|<q−d/2−1/2, so that there are no zeros of the zeta function in this region. This implies that the eigenvalues of Frobenius on E are at most qd/2+1/2 in absolute value (in fact it will soon be seen that they have absolute value exactly qd/2). This step of the argument is very similar to the usual proof that the Riemann zeta function has no zeros with real part greater than 1, by writing it as an Euler product.
- The conclusion of this is that the eigenvalues α of the Frobenius of a variety of even dimension d on the middle cohomology group satisfy
-
- To obtain the Riemann hypothesis one needs to eliminate the 1/2 from the exponent. This can be done as follows. Applying this estimate to any even power Vk of V and using the Kunneth formula shows that the eigenvalues of Frobenius on the middle cohomology of a variety V of any dimension d satisfy
- As this is true for arbitrarily large even k, this implies that
- Poincaré dualityPoincaré dualityIn mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
then implies that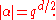
- This proves the Weil conjectures for the middle cohomology of a variety. The Weil conjectures for the cohomology below the middle dimension follow from this by applying the weak Lefschetz theorem, and the conjectures for cohomology above the middle dimension then follow from Poincaré duality.
Deligne's second proof
found and proved a generalization of the Weil conjectures, bounding the weights of the pushforward of a sheaf. In practice it is this generalization rather than the original Weil conjectures that is mostly used in applications, such as the hard Lefschetz theorem. Much of the second proof is a rearrangement of the ideas of his first proof. The main extra idea needed is an argument closely related to the theorem of Hadamard and de la Vallée Poussin, used by Deligne to show that various L-series do not have zeros with real part 1.A constructible sheaf on a variety over a finite field is called pure of weight β if for all points x the eigenvalues of the Frobenius at x all have absolute value N(x)β/2, and is called mixed of weight ≤β if it can be written as repeated extensions by pure sheaves with weights ≤β.
Deligne's theorem states that if f is a morphism of schemes of finite type over a finite field, then Rif! takes mixed sheaves of weight ≤β to mixed sheaves of weight ≤β+i.
The original Weil conjectures follow by taking f to be a morphism from a smooth projective variety to a point and considering the constant sheaf Ql on the variety. This gives an upper bound on the absolute values of the eigenvalues of Frobenius, and Poincaré duality then shows that this is also a lower bound.
In general Rif! does not take pure sheaves to pure sheaves. However it does when a suitable form of Poincaré duality holds, for example if f is smooth and proper, or if one works with perverse sheaves rather than sheaves as in .
Inspired by the work of on Morse theory
Morse theory
In differential topology, the techniques of Morse theory give a very direct way of analyzing the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a differentiable function on a manifold will, in a typical case, reflect...
, found another proof, using Deligne's l-adic Fourier transform
Fourier–Deligne transform
In algebraic geometry, the Fourier–Deligne transform, or ℓ-adic Fourier transform, or geometric Fourier transform, is an operation on objects of the derived category of ℓ-adic sheaves over the affine line. It was introduced by Pierre Deligne on November 29th, 1976 in a letter to David Kazhdan as...
, which allowed him to simplify Deligne's proof by avoiding the use of the method of Hadamard and de la Vallée Poussin. His proof generalizes the classical calculation of the absolute value of Gauss sum
Gauss sum
In mathematics, a Gauss sum or Gaussian sum is a particular kind of finite sum of roots of unity, typicallyG := G= \sum \chi\cdot \psi...
s using the fact that the norm of a Fourier transform has a simple relation to the norm of the original function. used Laumon's proof as the basis for their exposition of Deligne's theorem. gave a further simplification of Laumon's proof, using monodromy in the spirit of Deligne's first proof. gave another proof using the Fourier transform, replacing etale cohomology with rigid cohomology
Rigid cohomology
In mathematics, rigid cohomology is a p-adic cohomology theory introduced by . It extends crystalline cohomology to schemes that need not be proper or smooth, and extends Monsky–Washnitzer cohomology to non-affine varieties....
.