
Projective linear group
Encyclopedia
In mathematics
, especially in the group theoretic
area of algebra
, the projective linear group (also known as the projective general linear group or PGL) is the induced action
of the general linear group
of a vector space
V on the associated projective space
P(V). Explicitly, the projective linear group is the quotient group
where GL(V) is the general linear group
of V and Z(V) is the subgroup of all nonzero scalar transformations of V; these are quotiented out because they act trivially on the projective space and they form the kernel
of the action, and the notation "Z" reflects that the scalar transformations form the center of the general linear group.
The projective special linear group, PSL, is defined analogously, as the induced action of the special linear group
on the associated projective space. Explicitly:
where SL(V) is the special linear group over V and SZ(V) is the subgroup of scalar transformations with unit determinant
. Here SZ is the center of SL, and is naturally identified with the group of nth roots of unity in K (where n is the dimension of V and K is the base field).
PGL and PSL are some of the fundamental groups of study, part of the so-called classical groups, and an element of PGL is called a projective linear transformation. If V is the n-dimensional vector space over a field
F, namely the alternate notations PGL(n, F) and PSL(n, F) are also used.
Note that PGL(n, F) and PSL(n, F) are equal if and only if every element of F contains an nth root in F. As an example, note that but this corresponds to the real projective line being orientable, and the projective special linear group only being the orientation-preserving transformations.
PGL and PSL can also be defined over a ring, with an important example being the modular group
,
, where the projective group acting on homogeneous coordinates
(x0:x1: … :xn) is the underlying group of the geometry.This is therefore PGL(n + 1, F) for projective space
of dimension n Stated differently, the natural action
of GL(V) on V descends to an action of PGL(V) on the projective space P(V).
The projective linear groups therefore generalise the case PGL(2,C) of Möbius transformations (sometimes called the Möbius group), which acts on the projective line
.
Note that unlike the general linear group, which is generally defined axiomatically as "invertible functions preserving the linear (vector space) structure", the projective linear group is defined constructively, as a quotient of the general linear group of the associated vector space, rather than axiomatically as "invertible functions preserving the projective linear structure". This is reflected in the notation: PGL(n,F) is the group associated to GL(n,F), and is the projective linear group of (n − 1)-dimensional projective space, not n-dimensional projective space.
(a set of points P, lines L, and an incidence relation I specifying which points lie on which lines) satisfying certain axioms – an automorphism of a projective space thus defined then being an automorphism f of the set of points and an automorphism g of the set of lines, preserving the incidence relation,"Preserving the incidence relation" means that if point p is on line l then is in
is in  ; formally, if
; formally, if  then
then  . which is exactly a collineation of a space to itself. Projective linear transforms are collineations (planes in a vector space correspond to lines in the associated projective space, and linear transforms map planes to planes, so projective linear transforms map lines to lines), but in general not all collineations are projective linear transforms – PGL is in general a proper subgroup of the collineation group.
. which is exactly a collineation of a space to itself. Projective linear transforms are collineations (planes in a vector space correspond to lines in the associated projective space, and linear transforms map planes to planes, so projective linear transforms map lines to lines), but in general not all collineations are projective linear transforms – PGL is in general a proper subgroup of the collineation group.
Specifically, for (a projective line), all points are collinear, so the collineation group is exactly the symmetric group
(a projective line), all points are collinear, so the collineation group is exactly the symmetric group
of the points of the projective line, and except for and
and  (where PGL is the full symmetric group), PGL is a proper subgroup of the full symmetric group on these points.
(where PGL is the full symmetric group), PGL is a proper subgroup of the full symmetric group on these points.
For the collineation group is the projective semilinear group,
the collineation group is the projective semilinear group,  – this is PGL, twisted by field automorphisms; formally,
– this is PGL, twisted by field automorphisms; formally,  where k is the prime field for K; this is the fundamental theorem of projective geometry. Thus for K a prime field (
where k is the prime field for K; this is the fundamental theorem of projective geometry. Thus for K a prime field ( or
or  ), we have
), we have  but for K a field with non-trivial Galois automorphisms (such as
but for K a field with non-trivial Galois automorphisms (such as  for
for  or
or  ), the projective linear group is a proper subgroup of the collineation group, which can be thought of as "transforms preserving a projective semi-linear structure". Correspondingly, the quotient group
), the projective linear group is a proper subgroup of the collineation group, which can be thought of as "transforms preserving a projective semi-linear structure". Correspondingly, the quotient group  corresponds to "choices of linear structure", with the identity (base point) being the existing linear structure.
corresponds to "choices of linear structure", with the identity (base point) being the existing linear structure.
One may also define collineation groups for axiomatically defined projective spaces, where there is no natural notion of a projective linear transform. However, with the exception of the non-Desarguesian plane
s, all projective spaces are the projectivization of a linear space over a division ring
though, as noted above, there are multiple choices of linear structure, namely a torsor over (for
(for  ).
).
 A more familiar geometric way to understand the projective transforms is via projective rotations (the elements of PSO(n+1)), which corresponds to the stereographic projection
A more familiar geometric way to understand the projective transforms is via projective rotations (the elements of PSO(n+1)), which corresponds to the stereographic projection
of rotations of the unit hypersphere, and has dimension Visually, this corresponds to standing at the origin (or placing a camera at the origin), and turning one's angle of view, then projecting onto a flat plane. Rotations in axes perpendicular to the hyperplane preserve the hyperplane and yield a rotation of the hyperplane (an element of SO(n), which has dimension
Visually, this corresponds to standing at the origin (or placing a camera at the origin), and turning one's angle of view, then projecting onto a flat plane. Rotations in axes perpendicular to the hyperplane preserve the hyperplane and yield a rotation of the hyperplane (an element of SO(n), which has dimension  ), while rotations in axes parallel to the hyperplane are proper projective maps, and accounts for the remaining n dimensions.
), while rotations in axes parallel to the hyperplane are proper projective maps, and accounts for the remaining n dimensions.
 corresponding to the rational function
corresponding to the rational function

where multiplication of matrices agrees with composition of functions, and quotienting out by scalar matrices corresponding to multiplying the top and bottom of the fraction by a common factor. As with Möbius transformations, these functions can be interpreted as automorphisms of the projective line
over K.
finite field
Fq are often written as PSL(n,q) or Ln(q). They are finite simple groups whenever n is at least 2, with two exceptions: L2(2), which is isomorphic to S3, the symmetric group
on 3 letters, and is solvable
; and L2(3), which is isomorphic to A4, the alternating group on 4 letters, and is also solvable.
The special linear groups SL(n,q) are thus quasisimple: perfect central extensions of a simple group (unless and
and  or 3).
or 3).
in the 1830s, and were the second family of finite simple group
s, after the alternating groups. Galois constructed them as fractional linear transforms, and observed that they were simple except if p was 2 or 3; this is contained in his last letter to Chevalier. In the same letter and attached manuscripts, Galois also constructed the general linear group over a prime field, GL(ν, p), in studying the Galois group of the general equation of degree pν.
The groups PSL(n,q) (general n, general finite field) were then constructed in the classic 1870 text by Camille Jordan
, Traité des substitutions et des équations algébriques.
(qn − q)(qn − q2) … (qn − qn−1)/(q − 1) = qn2 – 1 – O(qn2 – 3)
which corresponds to the order of GL(n, q), divided by for projectivization; see q-analog
for projectivization; see q-analog
for discussion of such formulas. Note that the degree is n2 - 1, which agrees with the dimension as an algebraic group. The "O" is for big O notation
, meaning "terms involving lower order". This also equals the order of SL(n,q); there dividing by (q − 1) is due to the determinant.
The order of PSL(n, q) is the above, divided by , the number of scalar matrices with determinant 1 – or equivalently dividing by
, the number of scalar matrices with determinant 1 – or equivalently dividing by  , the number of classes of element that have no nth root, or equivalently, dividing by the number of nth roots of unity in
, the number of classes of element that have no nth root, or equivalently, dividing by the number of nth roots of unity in  .These are equal because they are the kernel and cokernel of the endomorphism
.These are equal because they are the kernel and cokernel of the endomorphism  formally,
formally,  More abstractly, the first realizes PSL as SL/SZ, while the second realizes PSL as the kernel of
More abstractly, the first realizes PSL as SL/SZ, while the second realizes PSL as the kernel of 
 , and
, and 
there are other exceptional isomorphisms between projective special linear groups and alternating groups (these groups are all simple, as the alternating group over 5 or more letters is simple):
 (see here for a proof)
(see here for a proof)

The isomorphism allows one to see the exotic outer automorphism of
allows one to see the exotic outer automorphism of  in terms of field automorphism and matrix operations. The isomorphism
in terms of field automorphism and matrix operations. The isomorphism  is of interest in the structure of the Mathieu group M24.
is of interest in the structure of the Mathieu group M24.
The associated extensions are covering groups of the alternating groups
are covering groups of the alternating groups
(universal perfect central extensions) for , by uniqueness of the universal perfect central extension; for
, by uniqueness of the universal perfect central extension; for  , the associated extension is a perfect central extension, but not universal: there is a 3-fold covering group
, the associated extension is a perfect central extension, but not universal: there is a 3-fold covering group
.
The groups over have a number of exceptional isomorphisms:
have a number of exceptional isomorphisms: the alternating group on five elements, or equivalently the icosahedral group;
the alternating group on five elements, or equivalently the icosahedral group; the symmetric group
the symmetric group
on five elements; the double cover of the alternating group A5
the double cover of the alternating group A5
, or equivalently the binary icosahedral group.
They can also be used to give a construction of an exotic map S5 → S6, as described below. Note however that GL(2,5) is not a double cover of but is rather a 4-fold cover.
but is rather a 4-fold cover.
A further isomorphism is: is the simple group of order 168, the second smallest non-abelian simple group, and is not an alternating group; see PSL(2,7)
is the simple group of order 168, the second smallest non-abelian simple group, and is not an alternating group; see PSL(2,7)
.
The above exceptional isomorphisms involving the projective special linear groups are almost all of the exceptional isomorphisms between families of finite simple groups; the only other exceptional isomorphism is between a projective special unitary group and a projective symplectic group.
between a projective special unitary group and a projective symplectic group.
 acts on the projective space
acts on the projective space  which has
which has  points, and this yields a map from the projective linear group to the symmetric group on
points, and this yields a map from the projective linear group to the symmetric group on  points. For
points. For  , this is the projective line
, this is the projective line  which has
which has  points, so there is a map
points, so there is a map  .
.
To understand these maps, it is useful to recall these facts:
Thus the image is a 3-transitive subgroup of known order, which allows it to be identified. This yields the following maps:
 points, non-trivial actions on fewer points are rarer. Indeed, for PSL(2,p) acts non-trivially on p points if and only if p = 2, 3, 5, 7, or 11; for 2 and 3 the group is not simple, while for 5, 7, and 11, the group is simple – further, it does not act non-trivially on fewer than p points.Since p divides the order of the group, the group does not embed in (or, since simple, map non-trivially to)
points, non-trivial actions on fewer points are rarer. Indeed, for PSL(2,p) acts non-trivially on p points if and only if p = 2, 3, 5, 7, or 11; for 2 and 3 the group is not simple, while for 5, 7, and 11, the group is simple – further, it does not act non-trivially on fewer than p points.Since p divides the order of the group, the group does not embed in (or, since simple, map non-trivially to)  for
for  as p does not divide the order of this latter group. This was first observed by Évariste Galois
as p does not divide the order of this latter group. This was first observed by Évariste Galois
in his last letter to Chevalier, 1832.
This can be analyzed as follows; note that for 2 and 3 the action is not faithful (it is a non-trivial quotient, and the PSL group is not simple), while for 5, 7, and 11 the action is faithful (as the group is simple and the action is non-trivial), and yields an embedding into Sp. In all but the last case, PSL(2,11), it corresponds to an exceptional isomorphism, where the right-most group has an obvious action on p points:
Further, L2(7) and L2(11) have two inequivalent actions on p points; geometrically this is realized by the action on a biplane, which has p points and p blocks – the action on the points and the action on the blocks are both actions on p points, but not conjugate (they have different point stabilizers); they are instead related by an outer automorphism of the group.
More recently, these last three exceptional actions have been interpreted as an example of the ADE classification
: these actions correspond to products (as sets, not as groups) of the groups as
 and
and  where the groups
where the groups 
 and
and  are the isometry groups of the Platonic solid
are the isometry groups of the Platonic solid
s, and correspond to and
and  under the McKay correspondence. These three exceptional cases are also realized as the geometries of polyhedra (equivalently, tilings of Riemann surfaces), respectively: the compound of five tetrahedra
under the McKay correspondence. These three exceptional cases are also realized as the geometries of polyhedra (equivalently, tilings of Riemann surfaces), respectively: the compound of five tetrahedra
inside the icosahedron (sphere, genus 0), the order 2 biplane (complementary Fano plane
) inside the Klein quartic (genus 3), and the order 3 biplane (Paley biplane) inside the buckyball surface (genus 70).
The action of can be seen algebraically as due to an exceptional inclusion
can be seen algebraically as due to an exceptional inclusion  – there are two conjugacy classes of subgroups of
– there are two conjugacy classes of subgroups of  that are isomorphic to
that are isomorphic to  each with 11 elements: the action of
each with 11 elements: the action of  by conjugation on these is an action on 11 points, and, further, the two conjugacy classes are related by an outer automorphism of
by conjugation on these is an action on 11 points, and, further, the two conjugacy classes are related by an outer automorphism of  (The same is true for subgroups of L2(7) isomorphic to S4, and this also has a biplane geometry.)
(The same is true for subgroups of L2(7) isomorphic to S4, and this also has a biplane geometry.)
Geometrically, this action can be understood via a biplane geometry, which is defined as follows. A biplane geometry is a symmetric design
(a set of points and an equal number of "lines", or rather blocks) such that any set of two points is contained in two lines, while any two lines intersect in two points; this is similar to a finite projective plane, except that rather than two points determining one line (and two lines determining one point), they determine two lines (respectively, points). In this case (the Paley biplane, obtained from the Paley digraph of order 11), the points are the affine line (the finite field) F11, where the first line is defined to be the five non-zero quadratic residues (points which are squares: 1, 3, 4, 5, 9), and the other lines are the affine translates of this (add a constant to all the points). is then isomorphic to the subgroup of S11 that preserve this geometry (sends lines to lines), giving a set of 11 points on which it acts – in fact two: the points or the lines, which corresponds to the outer automorphism – while
is then isomorphic to the subgroup of S11 that preserve this geometry (sends lines to lines), giving a set of 11 points on which it acts – in fact two: the points or the lines, which corresponds to the outer automorphism – while  is the stabilizer of a given line, or dually of a given point.
is the stabilizer of a given line, or dually of a given point.
More surprisingly, the coset space which has order 660/11 = 60 (and on which the icosahedral group acts) naturally has the structure of a buckeyball, which is used in the construction of the buckyball surface.
which has order 660/11 = 60 (and on which the icosahedral group acts) naturally has the structure of a buckeyball, which is used in the construction of the buckyball surface.
M24, one of the sporadic simple groups; in this context, one refers to PSL(3,4) as M21, though it is not properly a Mathieu group itself.
One begins with the projective plane over the field with four elements, which is a Steiner system
of type S(2,5,21) – meaning that it has 21 points, each line ("block", in Steiner terminology) has 5 points, and any 2 points determine a line – and on which PSL(3,4) acts. One calls this Steiner system W21 ("W" for Witt
), and then expands it to a larger Steiner system W24, expanding the symmetry group along the way: to the projective general linear group PGL(3,4), then to the projective semilinear group PΓL(3,4), and finally to the Mathieu group M24.
M24 also contains copies of PSL(2,11), which is maximal in M22, and PSL(2,23), which is maximal in M24, and can be used to construct M24.

PSL groups arise as Hurwitz groups (automorphism groups of Hurwitz surface
s – algebraic curves of maximal possibly symmetry group). The Hurwitz surface of lowest genus, the Klein quartic
(genus 3), has automorphism group isomorphic to PSL(2,7) (equivalently GL(3,2)), while the Hurwitz surface of second-lowest genus, the Macbeath surface
(genus 7), has automorphism group isomorphic to PSL(2,8).
In fact, many but not all simple groups arise as Hurwitz groups (including the monster group
, though not all alternating groups or sporadic groups), though PSL is notable for including the smallest such groups.
 arise in studying the modular group
arise in studying the modular group
, , as quotients by reducing all elements mod n; the kernels are called the principal congruence subgroups.
, as quotients by reducing all elements mod n; the kernels are called the principal congruence subgroups.
A noteworthy subgroup of the projective general linear group (and of the projective special linear group
(and of the projective special linear group  ) is the symmetries of the set
) is the symmetries of the set  In projective coordinates, the points
In projective coordinates, the points  are given by [0:1], [1:1], and [1:0], which explains why their stabilizer is represented by integral matrices. these also occur in the six cross-ratios. The subgroup can be expressed as fractional linear transformations, or represented (non-uniquely) by matrices, as:
are given by [0:1], [1:1], and [1:0], which explains why their stabilizer is represented by integral matrices. these also occur in the six cross-ratios. The subgroup can be expressed as fractional linear transformations, or represented (non-uniquely) by matrices, as:
Note that the top row is the identity and the two 3-cycles, and are orientation-preserving, forming a subgroup in while the bottom row is the three 2-cycles, and are in
while the bottom row is the three 2-cycles, and are in  and
and  but not in
but not in  hence realized either as matrices with determinant −1 and integer coefficients, or as matrices with determinant 1 and Gaussian integer
hence realized either as matrices with determinant −1 and integer coefficients, or as matrices with determinant 1 and Gaussian integer
coefficients.
This maps to the symmetries of under reduction mod n. Notably, for
under reduction mod n. Notably, for  this subgroup maps isomorphically to
this subgroup maps isomorphically to  This isomorphism can be seen by removing the minus signs in matrices, which yields the matrices for
This isomorphism can be seen by removing the minus signs in matrices, which yields the matrices for  and thus provides a splitting
and thus provides a splitting  for the quotient map
for the quotient map 
A further property of this subgroup is that the quotient map is realized by the group action. That is, the subgroup
is realized by the group action. That is, the subgroup  consisting of the 3-cycles and the identity
consisting of the 3-cycles and the identity  stabilizes the golden ratio
stabilizes the golden ratio
and inverse golden ratio while the 2-cycles interchange these, thus realizing the map.
while the 2-cycles interchange these, thus realizing the map.
The fixed points of the individual 2-cycles are, respectively, and this set is also preserved and permuted, corresponding to the action of
and this set is also preserved and permuted, corresponding to the action of  on the 2-cycles (its Sylow 2-subgroups) by conjugation and realizing the isomorphism
on the 2-cycles (its Sylow 2-subgroups) by conjugation and realizing the isomorphism 
s that define them:

via the long exact sequence of a fibration.
For both the reals and complexes, SL is a covering space of PSL, with number of sheets equal to the number of nth roots in K; thus in particular all their higher homotopy groups agree. For the reals, SL is a 2-fold cover of PSL for n even, and is a 1-fold cover for n odd, i.e., an isomorphism:

For the complexes, SL is an n-fold cover of PSL.
For PGL, for the reals, the fiber is so up to homotopy,
so up to homotopy,  is a 2-fold covering space, and all higher homotopy groups agree.
is a 2-fold covering space, and all higher homotopy groups agree.
For PGL over the complexes, the fiber is so up to homotopy,
so up to homotopy,  is a circle bundle. The higher homotopy groups of the circle vanish, so the homotopy groups of
is a circle bundle. The higher homotopy groups of the circle vanish, so the homotopy groups of  and
and  agree for
agree for  In fact,
In fact,  always vanishes for Lie groups, so the homotopy groups agree for
always vanishes for Lie groups, so the homotopy groups agree for 
 every connected Lie group whose Lie algebra is
every connected Lie group whose Lie algebra is  is a cover of PSL(n,F). Conversely, its universal covering group
is a cover of PSL(n,F). Conversely, its universal covering group
is the maximal (simply connected) element, and the intermediary realizations form a lattice of covering groups.
For example SL2(R) has center {±1} and fundamental group Z, and thus has universal cover and covers the centerless PSL2(R).
and covers the centerless PSL2(R).
 from a group G to a projective linear group is called a projective representation
from a group G to a projective linear group is called a projective representation
of the group G, by analogy with a linear representation (a homomorphism ). These were studied by Issai Schur
). These were studied by Issai Schur
, who showed that projective representations of G can be classified in terms of linear representations of central extensions of G. This led to the Schur multiplier
, which is used to address this question.
 though it can be defined for low dimensions.
though it can be defined for low dimensions.
For (or in fact
(or in fact  ) the projective space of
) the projective space of  is empty, as there are no 1-dimensional subspaces of a 0-dimensional space. Thus, PGL(0,K) is the trivial group, consisting of the unique empty map from the empty set
is empty, as there are no 1-dimensional subspaces of a 0-dimensional space. Thus, PGL(0,K) is the trivial group, consisting of the unique empty map from the empty set
to itself. Further, the action of scalars on a 0-dimensional space is trivial, so the map is trivial, rather than an inclusion as it is in higher dimensions.
is trivial, rather than an inclusion as it is in higher dimensions.
For the projective space of
the projective space of  is a single point, as there is a single 1-dimensional subspace. Thus, PGL(1,K) is the trivial group, consisting of the unique map from a singleton set to itself. Further, the general linear group of a 1-dimensional space is exactly the scalars, so the map
is a single point, as there is a single 1-dimensional subspace. Thus, PGL(1,K) is the trivial group, consisting of the unique map from a singleton set to itself. Further, the general linear group of a 1-dimensional space is exactly the scalars, so the map  is an isomorphism, corresponding to
is an isomorphism, corresponding to  being trivial.
being trivial.
For PGL(2,K) is non-trivial, but is unusual in that it is 3-transitive, unlike higher dimensions when it is only 2-transitive.
PGL(2,K) is non-trivial, but is unusual in that it is 3-transitive, unlike higher dimensions when it is only 2-transitive.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in the group theoretic
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
area of algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, the projective linear group (also known as the projective general linear group or PGL) is the induced action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
of a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V on the associated projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
P(V). Explicitly, the projective linear group is the quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
- PGL(V) = GL(V)/Z(V)
where GL(V) is the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
of V and Z(V) is the subgroup of all nonzero scalar transformations of V; these are quotiented out because they act trivially on the projective space and they form the kernel
Kernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
of the action, and the notation "Z" reflects that the scalar transformations form the center of the general linear group.
The projective special linear group, PSL, is defined analogously, as the induced action of the special linear group
Special linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
on the associated projective space. Explicitly:
- PSL(V) = SL(V)/SZ(V)
where SL(V) is the special linear group over V and SZ(V) is the subgroup of scalar transformations with unit determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
. Here SZ is the center of SL, and is naturally identified with the group of nth roots of unity in K (where n is the dimension of V and K is the base field).
PGL and PSL are some of the fundamental groups of study, part of the so-called classical groups, and an element of PGL is called a projective linear transformation. If V is the n-dimensional vector space over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F, namely the alternate notations PGL(n, F) and PSL(n, F) are also used.
Note that PGL(n, F) and PSL(n, F) are equal if and only if every element of F contains an nth root in F. As an example, note that but this corresponds to the real projective line being orientable, and the projective special linear group only being the orientation-preserving transformations.
PGL and PSL can also be defined over a ring, with an important example being the modular group
Modular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
,
Name
The name comes from projective geometryProjective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
, where the projective group acting on homogeneous coordinates
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
(x0:x1: … :xn) is the underlying group of the geometry.This is therefore PGL(n + 1, F) for projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
of dimension n Stated differently, the natural action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of GL(V) on V descends to an action of PGL(V) on the projective space P(V).
The projective linear groups therefore generalise the case PGL(2,C) of Möbius transformations (sometimes called the Möbius group), which acts on the projective line
Projective line
In mathematics, a projective line is a one-dimensional projective space. The projective line over a field K, denoted P1, may be defined as the set of one-dimensional subspaces of the two-dimensional vector space K2 .For the generalisation to the projective line over an associative ring, see...
.
Note that unlike the general linear group, which is generally defined axiomatically as "invertible functions preserving the linear (vector space) structure", the projective linear group is defined constructively, as a quotient of the general linear group of the associated vector space, rather than axiomatically as "invertible functions preserving the projective linear structure". This is reflected in the notation: PGL(n,F) is the group associated to GL(n,F), and is the projective linear group of (n − 1)-dimensional projective space, not n-dimensional projective space.
Collineations
A related group is the collineation group, which is defined axiomatically. A collineation is an invertible (or more generally one-to-one) map which sends collinear points to collinear points. One can define a projective space axiomatically in terms of an incidence structureIncidence structure
In mathematics, an incidence structure is a tripleC=.\,where P is a set of "points", L is a set of "lines" and I \subseteq P \times L is the incidence relation. The elements of I are called flags. If \in I,...
(a set of points P, lines L, and an incidence relation I specifying which points lie on which lines) satisfying certain axioms – an automorphism of a projective space thus defined then being an automorphism f of the set of points and an automorphism g of the set of lines, preserving the incidence relation,"Preserving the incidence relation" means that if point p is on line l then
 is in
is in  ; formally, if
; formally, if  then
then  . which is exactly a collineation of a space to itself. Projective linear transforms are collineations (planes in a vector space correspond to lines in the associated projective space, and linear transforms map planes to planes, so projective linear transforms map lines to lines), but in general not all collineations are projective linear transforms – PGL is in general a proper subgroup of the collineation group.
. which is exactly a collineation of a space to itself. Projective linear transforms are collineations (planes in a vector space correspond to lines in the associated projective space, and linear transforms map planes to planes, so projective linear transforms map lines to lines), but in general not all collineations are projective linear transforms – PGL is in general a proper subgroup of the collineation group.Specifically, for
 (a projective line), all points are collinear, so the collineation group is exactly the symmetric group
(a projective line), all points are collinear, so the collineation group is exactly the symmetric groupSymmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
of the points of the projective line, and except for
 and
and  (where PGL is the full symmetric group), PGL is a proper subgroup of the full symmetric group on these points.
(where PGL is the full symmetric group), PGL is a proper subgroup of the full symmetric group on these points.For
 the collineation group is the projective semilinear group,
the collineation group is the projective semilinear group,  – this is PGL, twisted by field automorphisms; formally,
– this is PGL, twisted by field automorphisms; formally,  where k is the prime field for K; this is the fundamental theorem of projective geometry. Thus for K a prime field (
where k is the prime field for K; this is the fundamental theorem of projective geometry. Thus for K a prime field ( or
or  ), we have
), we have  but for K a field with non-trivial Galois automorphisms (such as
but for K a field with non-trivial Galois automorphisms (such as  for
for  or
or  ), the projective linear group is a proper subgroup of the collineation group, which can be thought of as "transforms preserving a projective semi-linear structure". Correspondingly, the quotient group
), the projective linear group is a proper subgroup of the collineation group, which can be thought of as "transforms preserving a projective semi-linear structure". Correspondingly, the quotient group  corresponds to "choices of linear structure", with the identity (base point) being the existing linear structure.
corresponds to "choices of linear structure", with the identity (base point) being the existing linear structure.One may also define collineation groups for axiomatically defined projective spaces, where there is no natural notion of a projective linear transform. However, with the exception of the non-Desarguesian plane
Non-Desarguesian plane
In mathematics, a non-Desarguesian plane, named after Gérard Desargues, is a projective plane that does not satisfy Desargues's theorem, or in other words a plane that is not a Desarguesian plane...
s, all projective spaces are the projectivization of a linear space over a division ring
Division ring
In abstract algebra, a division ring, also called a skew field, is a ring in which division is possible. Specifically, it is a non-trivial ring in which every non-zero element a has a multiplicative inverse, i.e., an element x with...
though, as noted above, there are multiple choices of linear structure, namely a torsor over
 (for
(for  ).
).Elements
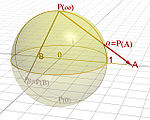
The elements of the projective linear group can be understood as "tilting the plane" along one of the axes, and then projecting to the original plane, and also have dimension n.
Stereographic projection
The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...
of rotations of the unit hypersphere, and has dimension
 Visually, this corresponds to standing at the origin (or placing a camera at the origin), and turning one's angle of view, then projecting onto a flat plane. Rotations in axes perpendicular to the hyperplane preserve the hyperplane and yield a rotation of the hyperplane (an element of SO(n), which has dimension
Visually, this corresponds to standing at the origin (or placing a camera at the origin), and turning one's angle of view, then projecting onto a flat plane. Rotations in axes perpendicular to the hyperplane preserve the hyperplane and yield a rotation of the hyperplane (an element of SO(n), which has dimension  ), while rotations in axes parallel to the hyperplane are proper projective maps, and accounts for the remaining n dimensions.
), while rotations in axes parallel to the hyperplane are proper projective maps, and accounts for the remaining n dimensions.Properties
- PGL sends collinear points to collinear points (it preserves projective lines), but it is not the full collineation group, which is instead either PΓL (for
 ) or the full symmetric groupSymmetric groupIn mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
) or the full symmetric groupSymmetric groupIn mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
for (the projective line).
(the projective line). - Every (biregular) algebraic automorphism of a projective space is projective linear. The birational automorphisms form a larger group, the Cremona groupCremona groupIn mathematics, in birational geometry, the Cremona group of order n over a field k is the group of birational automorphisms of the n-dimensional projective space over k...
. - PGL acts faithfully on projective space: non-identity elements act non-trivially.
- Concretely, the kernel of the action of GL on projective space is exactly the scalar maps, which are quotiented out in PGL.
- PGL acts 2-transitively on projective space.
- This is because 2 distinct points in projective space correspond to 2 vectors that do not lie on a single linear space, and hence are linearly independent, and GL acts transitively on k-element sets of linearly independent vectors.
- PGL(2, K) acts sharply 3-transitively on the projective line.
- 3 arbitrary points are conventionally mapped to
 in alternative notation,
in alternative notation,  In fractional linear transformation notation, the function
In fractional linear transformation notation, the function  maps
maps  and is the unique such map that does so. This is the cross-ratioCross-ratioIn geometry, the cross-ratio, also called double ratio and anharmonic ratio, is a special number associated with an ordered quadruple of collinear points, particularly points on a projective line...
and is the unique such map that does so. This is the cross-ratioCross-ratioIn geometry, the cross-ratio, also called double ratio and anharmonic ratio, is a special number associated with an ordered quadruple of collinear points, particularly points on a projective line...
 – see cross-ratio: transformational approach for details.
– see cross-ratio: transformational approach for details.
- 3 arbitrary points are conventionally mapped to
- For
 PGL(n, K) does not act 3-transitively, because it must send 3 collinear points to 3 other collinear points, not an arbitrary set. For
PGL(n, K) does not act 3-transitively, because it must send 3 collinear points to 3 other collinear points, not an arbitrary set. For  the space is the projective line, so all points are collinear and this is no restriction.
the space is the projective line, so all points are collinear and this is no restriction. - PGL(2, K) does not act 4-transitively on the projective line (except for
 as
as  has 3+1=4 points, so 3-transitive implies 4-transitive); the invariant that is preserved is the cross ratio, and this determines where every other point is sent: specifying where 3 points are mapped determines the map. Thus in particular it is not the full collineation group of the projective line (except for
has 3+1=4 points, so 3-transitive implies 4-transitive); the invariant that is preserved is the cross ratio, and this determines where every other point is sent: specifying where 3 points are mapped determines the map. Thus in particular it is not the full collineation group of the projective line (except for  and
and  ).
). - PSL(2, q) and PGL(2, q) (for q>2, and q odd for PSL) are two of the four families of Zassenhaus groupZassenhaus groupIn mathematics, a Zassenhaus group, named after Hans Julius Zassenhaus, is a certain sort of doubly transitive permutation group very closely related to rank-1 groups of Lie type.- Definition :...
s. - PSL(n, K) and PGL(n, K) are algebraic groupAlgebraic groupIn algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
s of dimension – they are both open subgroups of the projective space
– they are both open subgroups of the projective space 
- For PGL, the
 is the dimension of GL(n, K), and the
is the dimension of GL(n, K), and the  is from projectivization.
is from projectivization. - For PSL,
 is the dimension of SL, which is a covering space of PSL, so they have the same dimension. More casually, PSL differs from SL and from PGL by a finite group in each case, so the dimensions agree.
is the dimension of SL, which is a covering space of PSL, so they have the same dimension. More casually, PSL differs from SL and from PGL by a finite group in each case, so the dimensions agree. - This is also reflected in the order of the groups over finite fields, as the degree of the order as a polynomial in q: the order of PGL(n, q) is
 plus lower order terms.
plus lower order terms.
- For PGL, the
- PSL and PGL are centerless – this is because the diagonal matrices are not only the center, but also the hypercenter (the quotient of a group by its center is not necessarily centerless).For PSL (except PSL(2,2) and PSL(2,3)) this follows by Grün's lemma because SL is a perfect groupPerfect groupIn mathematics, more specifically in the area of modern algebra known as group theory, a group is said to be perfect if it equals its own commutator subgroup, or equivalently, if the group has no nontrivial abelian quotients...
(hence center equals hypercenter), but for PGL and the two exceptional PSLs this requires additional checking.
Fractional linear transformations
As for Möbius transformations, the group PGL(2, K) can be interpreted as fractional linear transformations with coefficients in K, a matrix corresponding to the rational function
corresponding to the rational functionRational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...

where multiplication of matrices agrees with composition of functions, and quotienting out by scalar matrices corresponding to multiplying the top and bottom of the fraction by a common factor. As with Möbius transformations, these functions can be interpreted as automorphisms of the projective line
Projective line
In mathematics, a projective line is a one-dimensional projective space. The projective line over a field K, denoted P1, may be defined as the set of one-dimensional subspaces of the two-dimensional vector space K2 .For the generalisation to the projective line over an associative ring, see...
over K.
Finite fields
The projective special linear groups PSL(n,Fq) for afinite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
Fq are often written as PSL(n,q) or Ln(q). They are finite simple groups whenever n is at least 2, with two exceptions: L2(2), which is isomorphic to S3, the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
on 3 letters, and is solvable
Solvable group
In mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
; and L2(3), which is isomorphic to A4, the alternating group on 4 letters, and is also solvable.
The special linear groups SL(n,q) are thus quasisimple: perfect central extensions of a simple group (unless
 and
and  or 3).
or 3).History
The groups PSL(2,p) were constructed by Évariste GaloisÉvariste Galois
Évariste Galois was a French mathematician born in Bourg-la-Reine. While still in his teens, he was able to determine a necessary and sufficient condition for a polynomial to be solvable by radicals, thereby solving a long-standing problem...
in the 1830s, and were the second family of finite simple group
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
s, after the alternating groups. Galois constructed them as fractional linear transforms, and observed that they were simple except if p was 2 or 3; this is contained in his last letter to Chevalier. In the same letter and attached manuscripts, Galois also constructed the general linear group over a prime field, GL(ν, p), in studying the Galois group of the general equation of degree pν.
The groups PSL(n,q) (general n, general finite field) were then constructed in the classic 1870 text by Camille Jordan
Camille Jordan
Marie Ennemond Camille Jordan was a French mathematician, known both for his foundational work in group theory and for his influential Cours d'analyse. He was born in Lyon and educated at the École polytechnique...
, Traité des substitutions et des équations algébriques.
Order
The order of PGL(n,q) is(qn − q)(qn − q2) … (qn − qn−1)/(q − 1) = qn2 – 1 – O(qn2 – 3)
which corresponds to the order of GL(n, q), divided by
 for projectivization; see q-analog
for projectivization; see q-analogQ-analog
Roughly speaking, in mathematics, specifically in the areas of combinatorics and special functions, a q-analog of a theorem, identity or expression is a generalization involving a new parameter q that returns the original theorem, identity or expression in the limit as q → 1...
for discussion of such formulas. Note that the degree is n2 - 1, which agrees with the dimension as an algebraic group. The "O" is for big O notation
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
, meaning "terms involving lower order". This also equals the order of SL(n,q); there dividing by (q − 1) is due to the determinant.
The order of PSL(n, q) is the above, divided by
 , the number of scalar matrices with determinant 1 – or equivalently dividing by
, the number of scalar matrices with determinant 1 – or equivalently dividing by  , the number of classes of element that have no nth root, or equivalently, dividing by the number of nth roots of unity in
, the number of classes of element that have no nth root, or equivalently, dividing by the number of nth roots of unity in  .These are equal because they are the kernel and cokernel of the endomorphism
.These are equal because they are the kernel and cokernel of the endomorphism  formally,
formally,  More abstractly, the first realizes PSL as SL/SZ, while the second realizes PSL as the kernel of
More abstractly, the first realizes PSL as SL/SZ, while the second realizes PSL as the kernel of 
Exceptional isomorphisms
In addition to the isomorphisms , and
, and 
there are other exceptional isomorphisms between projective special linear groups and alternating groups (these groups are all simple, as the alternating group over 5 or more letters is simple):

 (see here for a proof)
(see here for a proof)

The isomorphism
 allows one to see the exotic outer automorphism of
allows one to see the exotic outer automorphism of  in terms of field automorphism and matrix operations. The isomorphism
in terms of field automorphism and matrix operations. The isomorphism  is of interest in the structure of the Mathieu group M24.
is of interest in the structure of the Mathieu group M24.The associated extensions
 are covering groups of the alternating groups
are covering groups of the alternating groupsCovering groups of the alternating and symmetric groups
In the mathematical area of group theory, the covering groups of the alternating and symmetric groups are groups that are used to understand the projective representations of the alternating and symmetric groups...
(universal perfect central extensions) for
 , by uniqueness of the universal perfect central extension; for
, by uniqueness of the universal perfect central extension; for  , the associated extension is a perfect central extension, but not universal: there is a 3-fold covering group
, the associated extension is a perfect central extension, but not universal: there is a 3-fold covering groupSchur multiplier
In mathematical group theory, the Schur multiplier or Schur multiplicator is the second homology group H_2 of a group G.It was introduced by in his work on projective representations.-Examples and properties:...
.
The groups over
 have a number of exceptional isomorphisms:
have a number of exceptional isomorphisms: the alternating group on five elements, or equivalently the icosahedral group;
the alternating group on five elements, or equivalently the icosahedral group; the symmetric group
the symmetric groupSymmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
on five elements;
 the double cover of the alternating group A5
the double cover of the alternating group A5Covering groups of the alternating and symmetric groups
In the mathematical area of group theory, the covering groups of the alternating and symmetric groups are groups that are used to understand the projective representations of the alternating and symmetric groups...
, or equivalently the binary icosahedral group.
They can also be used to give a construction of an exotic map S5 → S6, as described below. Note however that GL(2,5) is not a double cover of
 but is rather a 4-fold cover.
but is rather a 4-fold cover.A further isomorphism is:
 is the simple group of order 168, the second smallest non-abelian simple group, and is not an alternating group; see PSL(2,7)
is the simple group of order 168, the second smallest non-abelian simple group, and is not an alternating group; see PSL(2,7)PSL(2,7)
In mathematics, the projective special linear group PSL is a finite simple group that has important applications in algebra, geometry, and number theory. It is the automorphism group of the Klein quartic as well as the symmetry group of the Fano plane...
.
The above exceptional isomorphisms involving the projective special linear groups are almost all of the exceptional isomorphisms between families of finite simple groups; the only other exceptional isomorphism is
 between a projective special unitary group and a projective symplectic group.
between a projective special unitary group and a projective symplectic group.Action on projective line
Some of the above maps can be seen directly in terms of the action of PSL and PGL on the associated projective line: acts on the projective space
acts on the projective space  which has
which has  points, and this yields a map from the projective linear group to the symmetric group on
points, and this yields a map from the projective linear group to the symmetric group on  points. For
points. For  , this is the projective line
, this is the projective line  which has
which has  points, so there is a map
points, so there is a map  .
.To understand these maps, it is useful to recall these facts:
- The order of
 is
is
- the order of
 either equals this (if the characteristic is 2), or is half this (if the characteristic is not 2).
either equals this (if the characteristic is 2), or is half this (if the characteristic is not 2).
- The action of the projective linear group on the projective line is sharptly 3-transitive (faithful and 3-transitive), so the map is one-to-one and has image a 3-transitive subgroup.
Thus the image is a 3-transitive subgroup of known order, which allows it to be identified. This yields the following maps:
-
 of order 6, which is an isomorphism.
of order 6, which is an isomorphism. -
 of orders 12 and 24, the latter of which is an isomorphism, with PSL(2,3) being the alternating group.
of orders 12 and 24, the latter of which is an isomorphism, with PSL(2,3) being the alternating group. -
 of order 60, yielding the alternating group
of order 60, yielding the alternating group 
-
 of orders 60 and 120, which yields an embedding of
of orders 60 and 120, which yields an embedding of  (respectively,
(respectively,  ) as a transitive subgroup of
) as a transitive subgroup of  (respectively,
(respectively,  ). This is an example of an exotic map S5 → S6, and can be used to construct the exceptional outer automorphism of S6. Note that the isomorphism
). This is an example of an exotic map S5 → S6, and can be used to construct the exceptional outer automorphism of S6. Note that the isomorphism  is not transparent from this presentation: there is no particularly natural set of 5 elements on which PGL(2,5) acts.
is not transparent from this presentation: there is no particularly natural set of 5 elements on which PGL(2,5) acts.
Action on p points
While PSL(n,q) naturally acts on points, non-trivial actions on fewer points are rarer. Indeed, for PSL(2,p) acts non-trivially on p points if and only if p = 2, 3, 5, 7, or 11; for 2 and 3 the group is not simple, while for 5, 7, and 11, the group is simple – further, it does not act non-trivially on fewer than p points.Since p divides the order of the group, the group does not embed in (or, since simple, map non-trivially to)
points, non-trivial actions on fewer points are rarer. Indeed, for PSL(2,p) acts non-trivially on p points if and only if p = 2, 3, 5, 7, or 11; for 2 and 3 the group is not simple, while for 5, 7, and 11, the group is simple – further, it does not act non-trivially on fewer than p points.Since p divides the order of the group, the group does not embed in (or, since simple, map non-trivially to)  for
for  as p does not divide the order of this latter group. This was first observed by Évariste Galois
as p does not divide the order of this latter group. This was first observed by Évariste GaloisÉvariste Galois
Évariste Galois was a French mathematician born in Bourg-la-Reine. While still in his teens, he was able to determine a necessary and sufficient condition for a polynomial to be solvable by radicals, thereby solving a long-standing problem...
in his last letter to Chevalier, 1832.
This can be analyzed as follows; note that for 2 and 3 the action is not faithful (it is a non-trivial quotient, and the PSL group is not simple), while for 5, 7, and 11 the action is faithful (as the group is simple and the action is non-trivial), and yields an embedding into Sp. In all but the last case, PSL(2,11), it corresponds to an exceptional isomorphism, where the right-most group has an obvious action on p points:
-
 via the sign map;
via the sign map; -
 via the quotient by the Klein 4-group;
via the quotient by the Klein 4-group; -
 To construct such an isomorphism, one needs to consider the group
To construct such an isomorphism, one needs to consider the group  as a Galois group of a Galois cover
as a Galois group of a Galois cover  , where
, where  is a modular curveModular curveIn number theory and algebraic geometry, a modular curve Y is a Riemann surface, or the corresponding algebraic curve, constructed as a quotient of the complex upper half-plane H by the action of a congruence subgroup Γ of the modular group of integral 2×2 matrices SL...
is a modular curveModular curveIn number theory and algebraic geometry, a modular curve Y is a Riemann surface, or the corresponding algebraic curve, constructed as a quotient of the complex upper half-plane H by the action of a congruence subgroup Γ of the modular group of integral 2×2 matrices SL...
of level N. This cover is ramified at 12 points. The modular curve X(5) has genus 0 and is isomorphic to a sphere over the field of complex numbers, and then the action of on these 12 points becomes the symmetry group of an icosahedronIcosahedral symmetryA regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...
on these 12 points becomes the symmetry group of an icosahedronIcosahedral symmetryA regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...
. One then needs to consider the action of the symmetry group of icosahedron on the five associated tetrahedraCompound of five tetrahedraThis compound polyhedron is also a stellation of the regular icosahedron. It was first described by Edmund Hess in 1876.-As a compound:It can be constructed by arranging five tetrahedra in rotational icosahedral symmetry , as colored in the upper right model...
. -
 which acts on the 1+2+4 = 7 points of the Fano planeFano planeIn finite geometry, the Fano plane is the finite projective plane with the smallest possible number of points and lines: 7 each.-Homogeneous coordinates:...
which acts on the 1+2+4 = 7 points of the Fano planeFano planeIn finite geometry, the Fano plane is the finite projective plane with the smallest possible number of points and lines: 7 each.-Homogeneous coordinates:...
(projective plane over F2); this can also be seen as the action on order 2 biplane, which is the complementary Fano plane. -
 is subtler, and elaborated below; it acts on the order 3 biplane.
is subtler, and elaborated below; it acts on the order 3 biplane.
Further, L2(7) and L2(11) have two inequivalent actions on p points; geometrically this is realized by the action on a biplane, which has p points and p blocks – the action on the points and the action on the blocks are both actions on p points, but not conjugate (they have different point stabilizers); they are instead related by an outer automorphism of the group.
More recently, these last three exceptional actions have been interpreted as an example of the ADE classification
ADE classification
In mathematics, the ADE classification is the complete list of simply laced Dynkin diagrams or other mathematical objects satisfying analogous axioms; "simply laced" means that there are no multiple edges, which corresponds to all simple roots in the root system forming angles of \pi/2 = 90^\circ ...
: these actions correspond to products (as sets, not as groups) of the groups as

 and
and  where the groups
where the groups 
 and
and  are the isometry groups of the Platonic solid
are the isometry groups of the Platonic solidPlatonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s, and correspond to
 and
and  under the McKay correspondence. These three exceptional cases are also realized as the geometries of polyhedra (equivalently, tilings of Riemann surfaces), respectively: the compound of five tetrahedra
under the McKay correspondence. These three exceptional cases are also realized as the geometries of polyhedra (equivalently, tilings of Riemann surfaces), respectively: the compound of five tetrahedraCompound of five tetrahedra
This compound polyhedron is also a stellation of the regular icosahedron. It was first described by Edmund Hess in 1876.-As a compound:It can be constructed by arranging five tetrahedra in rotational icosahedral symmetry , as colored in the upper right model...
inside the icosahedron (sphere, genus 0), the order 2 biplane (complementary Fano plane
Fano plane
In finite geometry, the Fano plane is the finite projective plane with the smallest possible number of points and lines: 7 each.-Homogeneous coordinates:...
) inside the Klein quartic (genus 3), and the order 3 biplane (Paley biplane) inside the buckyball surface (genus 70).
The action of
 can be seen algebraically as due to an exceptional inclusion
can be seen algebraically as due to an exceptional inclusion  – there are two conjugacy classes of subgroups of
– there are two conjugacy classes of subgroups of  that are isomorphic to
that are isomorphic to  each with 11 elements: the action of
each with 11 elements: the action of  by conjugation on these is an action on 11 points, and, further, the two conjugacy classes are related by an outer automorphism of
by conjugation on these is an action on 11 points, and, further, the two conjugacy classes are related by an outer automorphism of  (The same is true for subgroups of L2(7) isomorphic to S4, and this also has a biplane geometry.)
(The same is true for subgroups of L2(7) isomorphic to S4, and this also has a biplane geometry.)Geometrically, this action can be understood via a biplane geometry, which is defined as follows. A biplane geometry is a symmetric design
Symmetric design
In combinatorial mathematics, a symmetric design is a block design with equal numbers of points and blocks. Thus, it has the fewest possible blocks given the number of points . They are also known as projective designs....
(a set of points and an equal number of "lines", or rather blocks) such that any set of two points is contained in two lines, while any two lines intersect in two points; this is similar to a finite projective plane, except that rather than two points determining one line (and two lines determining one point), they determine two lines (respectively, points). In this case (the Paley biplane, obtained from the Paley digraph of order 11), the points are the affine line (the finite field) F11, where the first line is defined to be the five non-zero quadratic residues (points which are squares: 1, 3, 4, 5, 9), and the other lines are the affine translates of this (add a constant to all the points).
 is then isomorphic to the subgroup of S11 that preserve this geometry (sends lines to lines), giving a set of 11 points on which it acts – in fact two: the points or the lines, which corresponds to the outer automorphism – while
is then isomorphic to the subgroup of S11 that preserve this geometry (sends lines to lines), giving a set of 11 points on which it acts – in fact two: the points or the lines, which corresponds to the outer automorphism – while  is the stabilizer of a given line, or dually of a given point.
is the stabilizer of a given line, or dually of a given point.More surprisingly, the coset space
 which has order 660/11 = 60 (and on which the icosahedral group acts) naturally has the structure of a buckeyball, which is used in the construction of the buckyball surface.
which has order 660/11 = 60 (and on which the icosahedral group acts) naturally has the structure of a buckeyball, which is used in the construction of the buckyball surface.Mathieu groups
The group PSL(3,4) can be used to construct the Mathieu groupMathieu group
In the mathematical field of group theory, the Mathieu groups, named after the French mathematician Émile Léonard Mathieu, are five finite simple groups he discovered and reported in papers in 1861 and 1873; these were the first sporadic simple groups discovered...
M24, one of the sporadic simple groups; in this context, one refers to PSL(3,4) as M21, though it is not properly a Mathieu group itself.
One begins with the projective plane over the field with four elements, which is a Steiner system
Steiner system
250px|right|thumbnail|The [[Fano plane]] is an S Steiner triple system. The blocks are the 7 lines, each containing 3 points. Every pair of points belongs to a unique line....
of type S(2,5,21) – meaning that it has 21 points, each line ("block", in Steiner terminology) has 5 points, and any 2 points determine a line – and on which PSL(3,4) acts. One calls this Steiner system W21 ("W" for Witt
Ernst Witt
Ernst Witt was a German mathematician born on the island of Als . Shortly after his birth, he and his parents moved to China, and he did not return to Europe until he was nine....
), and then expands it to a larger Steiner system W24, expanding the symmetry group along the way: to the projective general linear group PGL(3,4), then to the projective semilinear group PΓL(3,4), and finally to the Mathieu group M24.
M24 also contains copies of PSL(2,11), which is maximal in M22, and PSL(2,23), which is maximal in M24, and can be used to construct M24.
Hurwitz surfaces

PSL groups arise as Hurwitz groups (automorphism groups of Hurwitz surface
Hurwitz surface
In Riemann surface theory and hyperbolic geometry, a Hurwitz surface, named after Adolf Hurwitz, is a compact Riemann surface with preciselyautomorphisms, where g is the genus of the surface. This number is maximal by virtue of Hurwitz's theorem on automorphisms...
s – algebraic curves of maximal possibly symmetry group). The Hurwitz surface of lowest genus, the Klein quartic
Klein quartic
In hyperbolic geometry, the Klein quartic, named after Felix Klein, is a compact Riemann surface of genus 3 with the highest possible order automorphism group for this genus, namely order 168 orientation-preserving automorphisms, and 336 automorphisms if orientation may be reversed...
(genus 3), has automorphism group isomorphic to PSL(2,7) (equivalently GL(3,2)), while the Hurwitz surface of second-lowest genus, the Macbeath surface
Macbeath surface
In Riemann surface theory and hyperbolic geometry, the Macbeath surface, also called Macbeath's curve or the Fricke–Macbeath curve, is the genus-7 Hurwitz surface....
(genus 7), has automorphism group isomorphic to PSL(2,8).
In fact, many but not all simple groups arise as Hurwitz groups (including the monster group
Monster group
In the mathematical field of group theory, the Monster group M or F1 is a group of finite order:...
, though not all alternating groups or sporadic groups), though PSL is notable for including the smallest such groups.
Modular group
The groups arise in studying the modular group
arise in studying the modular groupModular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
,
 , as quotients by reducing all elements mod n; the kernels are called the principal congruence subgroups.
, as quotients by reducing all elements mod n; the kernels are called the principal congruence subgroups.A noteworthy subgroup of the projective general linear group
 (and of the projective special linear group
(and of the projective special linear group  ) is the symmetries of the set
) is the symmetries of the set  In projective coordinates, the points
In projective coordinates, the points  are given by [0:1], [1:1], and [1:0], which explains why their stabilizer is represented by integral matrices. these also occur in the six cross-ratios. The subgroup can be expressed as fractional linear transformations, or represented (non-uniquely) by matrices, as:
are given by [0:1], [1:1], and [1:0], which explains why their stabilizer is represented by integral matrices. these also occur in the six cross-ratios. The subgroup can be expressed as fractional linear transformations, or represented (non-uniquely) by matrices, as:
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Note that the top row is the identity and the two 3-cycles, and are orientation-preserving, forming a subgroup in
 while the bottom row is the three 2-cycles, and are in
while the bottom row is the three 2-cycles, and are in  and
and  but not in
but not in  hence realized either as matrices with determinant −1 and integer coefficients, or as matrices with determinant 1 and Gaussian integer
hence realized either as matrices with determinant −1 and integer coefficients, or as matrices with determinant 1 and Gaussian integerGaussian integer
In number theory, a Gaussian integer is a complex number whose real and imaginary part are both integers. The Gaussian integers, with ordinary addition and multiplication of complex numbers, form an integral domain, usually written as Z[i]. The Gaussian integers are a special case of the quadratic...
coefficients.
This maps to the symmetries of
 under reduction mod n. Notably, for
under reduction mod n. Notably, for  this subgroup maps isomorphically to
this subgroup maps isomorphically to  This isomorphism can be seen by removing the minus signs in matrices, which yields the matrices for
This isomorphism can be seen by removing the minus signs in matrices, which yields the matrices for  and thus provides a splitting
and thus provides a splitting  for the quotient map
for the quotient map 
A further property of this subgroup is that the quotient map
 is realized by the group action. That is, the subgroup
is realized by the group action. That is, the subgroup  consisting of the 3-cycles and the identity
consisting of the 3-cycles and the identity  stabilizes the golden ratio
stabilizes the golden ratioGolden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
and inverse golden ratio
 while the 2-cycles interchange these, thus realizing the map.
while the 2-cycles interchange these, thus realizing the map.The fixed points of the individual 2-cycles are, respectively,
 and this set is also preserved and permuted, corresponding to the action of
and this set is also preserved and permuted, corresponding to the action of  on the 2-cycles (its Sylow 2-subgroups) by conjugation and realizing the isomorphism
on the 2-cycles (its Sylow 2-subgroups) by conjugation and realizing the isomorphism 
Topology
Over the real and complex numbers, the topology of PGL and PSL can be determined from the fiber bundleFiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
s that define them:


via the long exact sequence of a fibration.
For both the reals and complexes, SL is a covering space of PSL, with number of sheets equal to the number of nth roots in K; thus in particular all their higher homotopy groups agree. For the reals, SL is a 2-fold cover of PSL for n even, and is a 1-fold cover for n odd, i.e., an isomorphism:


For the complexes, SL is an n-fold cover of PSL.
For PGL, for the reals, the fiber is
 so up to homotopy,
so up to homotopy,  is a 2-fold covering space, and all higher homotopy groups agree.
is a 2-fold covering space, and all higher homotopy groups agree.For PGL over the complexes, the fiber is
 so up to homotopy,
so up to homotopy,  is a circle bundle. The higher homotopy groups of the circle vanish, so the homotopy groups of
is a circle bundle. The higher homotopy groups of the circle vanish, so the homotopy groups of  and
and  agree for
agree for  In fact,
In fact,  always vanishes for Lie groups, so the homotopy groups agree for
always vanishes for Lie groups, so the homotopy groups agree for 
Covering groups
Over the real and complex numbers, the projective special linear groups are the minimal (centerless) Lie group realizations for the special linear Lie algebra every connected Lie group whose Lie algebra is
every connected Lie group whose Lie algebra is  is a cover of PSL(n,F). Conversely, its universal covering group
is a cover of PSL(n,F). Conversely, its universal covering groupUniversal covering group
In mathematics, a covering group of a topological group H is a covering space G of H such that G is a topological group and the covering map p : G → H is a continuous group homomorphism. The map p is called the covering homomorphism...
is the maximal (simply connected) element, and the intermediary realizations form a lattice of covering groups.
For example SL2(R) has center {±1} and fundamental group Z, and thus has universal cover
 and covers the centerless PSL2(R).
and covers the centerless PSL2(R).Representation theory
A group homomorphismGroup homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
 from a group G to a projective linear group is called a projective representation
from a group G to a projective linear group is called a projective representationProjective representation
In the mathematical field of representation theory, a projective representation of a group G on a vector space V over a field F is a group homomorphism from G to the projective linear groupwhere GL is the general linear group of invertible linear transformations of V over F and F* here is the...
of the group G, by analogy with a linear representation (a homomorphism
 ). These were studied by Issai Schur
). These were studied by Issai SchurIssai Schur
Issai Schur was a mathematician who worked in Germany for most of his life. He studied at Berlin...
, who showed that projective representations of G can be classified in terms of linear representations of central extensions of G. This led to the Schur multiplier
Schur multiplier
In mathematical group theory, the Schur multiplier or Schur multiplicator is the second homology group H_2 of a group G.It was introduced by in his work on projective representations.-Examples and properties:...
, which is used to address this question.
Low dimensions
The projective linear group is mostly studied for though it can be defined for low dimensions.
though it can be defined for low dimensions.For
 (or in fact
(or in fact  ) the projective space of
) the projective space of  is empty, as there are no 1-dimensional subspaces of a 0-dimensional space. Thus, PGL(0,K) is the trivial group, consisting of the unique empty map from the empty set
is empty, as there are no 1-dimensional subspaces of a 0-dimensional space. Thus, PGL(0,K) is the trivial group, consisting of the unique empty map from the empty setEmpty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
to itself. Further, the action of scalars on a 0-dimensional space is trivial, so the map
 is trivial, rather than an inclusion as it is in higher dimensions.
is trivial, rather than an inclusion as it is in higher dimensions.For
 the projective space of
the projective space of  is a single point, as there is a single 1-dimensional subspace. Thus, PGL(1,K) is the trivial group, consisting of the unique map from a singleton set to itself. Further, the general linear group of a 1-dimensional space is exactly the scalars, so the map
is a single point, as there is a single 1-dimensional subspace. Thus, PGL(1,K) is the trivial group, consisting of the unique map from a singleton set to itself. Further, the general linear group of a 1-dimensional space is exactly the scalars, so the map  is an isomorphism, corresponding to
is an isomorphism, corresponding to  being trivial.
being trivial.For
 PGL(2,K) is non-trivial, but is unusual in that it is 3-transitive, unlike higher dimensions when it is only 2-transitive.
PGL(2,K) is non-trivial, but is unusual in that it is 3-transitive, unlike higher dimensions when it is only 2-transitive.Examples
- PSL(2,7)PSL(2,7)In mathematics, the projective special linear group PSL is a finite simple group that has important applications in algebra, geometry, and number theory. It is the automorphism group of the Klein quartic as well as the symmetry group of the Fano plane...
- Modular groupModular groupIn mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
, PSL(2,Z) - PSL(2,R)
- Möbius group, PGL(2,C) = PSL(2,C)
Subgroups
- Projective orthogonal groupProjective orthogonal groupIn projective geometry and linear algebra, the projective orthogonal group PO is the induced action of the orthogonal group of a quadratic space V = A quadratic space is a vector space V together with a quadratic form Q; the Q is dropped from notation when it is clear. on the associated projective...
, PO – maximal compact subgroupMaximal compact subgroupIn mathematics, a maximal compact subgroup K of a topological group G is a subgroup K that is a compact space, in the subspace topology, and maximal amongst such subgroups....
of PGL - Projective unitary groupProjective unitary groupIn mathematics, the projective unitary group PU is the quotient of the unitary group U by the right multiplication of its center, U, embedded as scalars....
, PU - Projective special orthogonal group, PSO – maximal compact subgroup of PSL
- Projective special unitary group, PSU
Larger groups
The projective linear group is contained within larger groups, notably:- Projective semilinear group, PΓL, which allows field automorphisms.
- Cremona groupCremona groupIn mathematics, in birational geometry, the Cremona group of order n over a field k is the group of birational automorphisms of the n-dimensional projective space over k...
, of birational automorphisms; any biregular automorphism is linear, so PGL coincides with the group of biregular automorphisms.
of birational automorphisms; any biregular automorphism is linear, so PGL coincides with the group of biregular automorphisms.

