
Group extension
Encyclopedia
In mathematics
, a group extension is a general means of describing a group
in terms of a particular normal subgroup
and quotient group
. If Q and N are two groups, then G is an extension of Q by N if there is a short exact sequence

If G is an extension of Q by N, then G is a group, N is a normal subgroup
of G and the quotient group
G/N is isomorphic to group Q. Group extensions arise in the context of the extension problem, where the groups Q and N are known and the properties of G are to be determined.
An extension is called a central extension if the subgroup N lies in the center of G.
, is immediately obvious. If one requires G and Q to be abelian group
s, then the set of isomorphism classes of extensions of Q by a given (abelian) group N is in fact a group, which is isomorphic to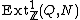 ;
;
cf. the Ext functor
. Several other general classes of extensions are known but no theory exists which treats all the possible extensions at one time. Group extension is usually described as a hard problem; it is termed the extension problem.
To consider some examples, if G = H × K, then G is an extension of both H and K. More generally, if G is a semidirect product
of K and H, then G is an extension of H by K, so such products as the wreath product
provide further examples of extensions.
of a finite group is a finite sequence of subgroups {Ai}, where each Ai+1 is an extension of Ai by some simple group
. The classification of finite simple groups
would give us a complete list of finite simple groups; so the solution to the extension problem would give us enough information to construct and classify all finite groups in general.
We can use the language of diagrams to provide a more flexible definition of extension: a group G is an extension of a group H by a group K if and only if there is an exact sequence
:

where 1 denotes the trivial group with a single element. This definition is more general in that it does not require that K be a subgroup of G; instead, K is isomorphic to a normal subgroup
K* of G, and H is isomorphic to G/K*.
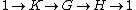
for which there is a homomorphism
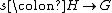 such that going from H to G by s and then back to H by the quotient map of the short exact sequence induces the identity map
such that going from H to G by s and then back to H by the quotient map of the short exact sequence induces the identity map
on H. In this situation, it is usually said that s splits the above exact sequence
.
Split extensions are very easy to classify, because the splitting lemma
states that an extension is split if and only if
the group G is a semidirect product
of K and H. Semidirect products themselves are easy to classify, because they are in one-to-one correspondence with homomorphisms from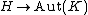 , where Aut(K) is the automorphism
, where Aut(K) is the automorphism
group of K. For a full discussion of why this is true, see semidirect product
.
. However in group theory the opposite terminology has crept in, partly because of the notation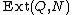 , which reads easily as extensions of Q by N, and the focus is on the group Q.
, which reads easily as extensions of Q by N, and the focus is on the group Q.
The paper of Brown and Porter (1996) on the Schreier
theory of nonabelian extensions (cited below) uses the terminology that an extension of K gives a larger structure.
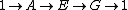
such that A is in Z(E), the center of the group E. The set of isomorphism classes of central extensions of G by A is in one-to-one correspondence with the cohomology
group H2(G,A), where the action of G on A is trivial.
Examples of central extensions can be constructed by taking any group G and any abelian group
A, and setting E to be A×G. This kind of split example (a split extension in the sense of the extension problem, since G is present as a subgroup of E) isn't of particular interest, since it corresponds to the element 0 in H2(G,A) under the above correspondence. More serious examples are found in the theory of projective representation
s, in cases where the projective representation cannot be lifted to an ordinary linear representation.
In the case of finite perfect groups, there is a universal perfect central extension.
Similarly, the central extension of a Lie algebra
is an exact sequence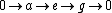
such that is in the center of
is in the center of  .
.
There is a general theory of central extensions in Maltsev varieties, see the paper by Janelidze and Kelly listed below.
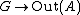 , a tedious but explicitly checkable existence condition involving H3(G,Z(A)) and the cohomology group H2(G,Z(A)).
, a tedious but explicitly checkable existence condition involving H3(G,Z(A)) and the cohomology group H2(G,Z(A)).
theory, central extensions arise in connection with algebraic topology
. Roughly speaking, central extensions of Lie groups by discrete groups are the same as covering groups. More precisely, a connected
covering space G* of a connected Lie group G is naturally a central extension of G, in such a way that the projection
is a group homomorphism, and surjective. (The group structure on G* depends on the choice of an identity element mapping to the identity in G.) For example, when G* is the universal cover of G, the kernel of π is the fundamental group
of G, which is known to be abelian (see H-space
). Conversely, given a Lie group G and a discrete central subgroup Z, the quotient G/Z is a Lie group and G is a covering space of it.
More generally, when the groups A, E and G occurring in a central extension are Lie groups, and the maps between them are homomorphism of Lie groups, then the Lie algebra of E is a central extension of the Lie algebra of G by the Lie algebra of A. In the terminology of theoretical physics
, generators of Lie(A) are called central charge
s. These generators are in the center of the Lie algebra of E; by Noether's theorem
, generators of symmetry groups correspond to conserved quantities, referred to as charges
.
The basic examples of central extensions as covering groups are:
The case of SL2(R) involves a fundamental group that is infinite cyclic. Here the central extension involved is well known in modular form
theory, in the case of forms of weight ½. A projective representation that corresponds is the Weil representation, constructed from the Fourier transform
, in this case on the real line
. Metaplectic groups also occur in quantum mechanics
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a group extension is a general means of describing a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
in terms of a particular normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
and quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
. If Q and N are two groups, then G is an extension of Q by N if there is a short exact sequence

If G is an extension of Q by N, then G is a group, N is a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of G and the quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
G/N is isomorphic to group Q. Group extensions arise in the context of the extension problem, where the groups Q and N are known and the properties of G are to be determined.
An extension is called a central extension if the subgroup N lies in the center of G.
Extensions in general
One extension, the direct productDirect product of groups
In the mathematical field of group theory, the direct product is an operation that takes two groups and and constructs a new group, usually denoted...
, is immediately obvious. If one requires G and Q to be abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s, then the set of isomorphism classes of extensions of Q by a given (abelian) group N is in fact a group, which is isomorphic to
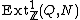 ;
;cf. the Ext functor
Ext functor
In mathematics, the Ext functors of homological algebra are derived functors of Hom functors. They were first used in algebraic topology, but are common in many areas of mathematics.- Definition and computation :...
. Several other general classes of extensions are known but no theory exists which treats all the possible extensions at one time. Group extension is usually described as a hard problem; it is termed the extension problem.
To consider some examples, if G = H × K, then G is an extension of both H and K. More generally, if G is a semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of K and H, then G is an extension of H by K, so such products as the wreath product
Wreath product
In mathematics, the wreath product of group theory is a specialized product of two groups, based on a semidirect product. Wreath products are an important tool in the classification of permutation groups and also provide a way of constructing interesting examples of groups.Given two groups A and H...
provide further examples of extensions.
Extension problem
The question of what groups G are extensions of H is called the extension problem, and has been studied heavily since the late nineteenth century. As to its motivation, consider that the composition seriesComposition series
In abstract algebra, a composition series provides a way to break up an algebraic structure, such as a group or a module, into simple pieces. The need for considering composition series in the context of modules arises from the fact that many naturally occurring modules are not semisimple, hence...
of a finite group is a finite sequence of subgroups {Ai}, where each Ai+1 is an extension of Ai by some simple group
Simple group
In mathematics, a simple group is a nontrivial group whose only normal subgroups are the trivial group and the group itself. A group that is not simple can be broken into two smaller groups, a normal subgroup and the quotient group, and the process can be repeated...
. The classification of finite simple groups
Classification of finite simple groups
In mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
would give us a complete list of finite simple groups; so the solution to the extension problem would give us enough information to construct and classify all finite groups in general.
We can use the language of diagrams to provide a more flexible definition of extension: a group G is an extension of a group H by a group K if and only if there is an exact sequence
Exact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
:

where 1 denotes the trivial group with a single element. This definition is more general in that it does not require that K be a subgroup of G; instead, K is isomorphic to a normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
K* of G, and H is isomorphic to G/K*.
Classifying extensions
Solving the extension problem amounts to classifying all extensions of H by K; or more practically, by expressing all such extensions in terms of mathematical objects that are easier to understand and compute. In general, this problem is very hard, and all the most useful results classify extensions that satisfy some additional condition.Classifying split extensions
A split extension is an extension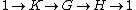
for which there is a homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
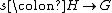 such that going from H to G by s and then back to H by the quotient map of the short exact sequence induces the identity map
such that going from H to G by s and then back to H by the quotient map of the short exact sequence induces the identity mapIdentity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
on H. In this situation, it is usually said that s splits the above exact sequence
Exact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
.
Split extensions are very easy to classify, because the splitting lemma
Splitting lemma
In mathematics, and more specifically in homological algebra, the splitting lemma states that in any abelian category, the following statements for short exact sequence are equivalent....
states that an extension is split if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the group G is a semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of K and H. Semidirect products themselves are easy to classify, because they are in one-to-one correspondence with homomorphisms from
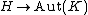 , where Aut(K) is the automorphism
, where Aut(K) is the automorphismAutomorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
group of K. For a full discussion of why this is true, see semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
.
Warning
In general in mathematics, an extension of a structure K is usually regarded as a structure L of which K is a substructure. See for example field extensionField extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
. However in group theory the opposite terminology has crept in, partly because of the notation
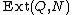 , which reads easily as extensions of Q by N, and the focus is on the group Q.
, which reads easily as extensions of Q by N, and the focus is on the group Q.The paper of Brown and Porter (1996) on the Schreier
Otto Schreier
Otto Schreier was an Austrian mathematician who made major contributions in combinatorial group theory and in the topology of Lie groups. He studied mathematics at the University of Vienna and obtained his doctorate in 1923, under the supervision of Philipp Furtwängler...
theory of nonabelian extensions (cited below) uses the terminology that an extension of K gives a larger structure.
Central extension
A central extension of a group G is a short exact sequence of groups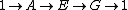
such that A is in Z(E), the center of the group E. The set of isomorphism classes of central extensions of G by A is in one-to-one correspondence with the cohomology
Group cohomology
In abstract algebra, homological algebra, algebraic topology and algebraic number theory, as well as in applications to group theory proper, group cohomology is a way to study groups using a sequence of functors H n. The study of fixed points of groups acting on modules and quotient modules...
group H2(G,A), where the action of G on A is trivial.
Examples of central extensions can be constructed by taking any group G and any abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
A, and setting E to be A×G. This kind of split example (a split extension in the sense of the extension problem, since G is present as a subgroup of E) isn't of particular interest, since it corresponds to the element 0 in H2(G,A) under the above correspondence. More serious examples are found in the theory of projective representation
Projective representation
In the mathematical field of representation theory, a projective representation of a group G on a vector space V over a field F is a group homomorphism from G to the projective linear groupwhere GL is the general linear group of invertible linear transformations of V over F and F* here is the...
s, in cases where the projective representation cannot be lifted to an ordinary linear representation.
In the case of finite perfect groups, there is a universal perfect central extension.
Similarly, the central extension of a Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
is an exact sequence
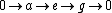
such that
 is in the center of
is in the center of  .
.There is a general theory of central extensions in Maltsev varieties, see the paper by Janelidze and Kelly listed below.
Generalization to general extensions
The paper on Group Extensions and H3 given below provides a similar classification of all extensions of G by A in terms of homomorphisms from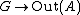 , a tedious but explicitly checkable existence condition involving H3(G,Z(A)) and the cohomology group H2(G,Z(A)).
, a tedious but explicitly checkable existence condition involving H3(G,Z(A)) and the cohomology group H2(G,Z(A)).Lie groups
In Lie groupLie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
theory, central extensions arise in connection with algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
. Roughly speaking, central extensions of Lie groups by discrete groups are the same as covering groups. More precisely, a connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
covering space G* of a connected Lie group G is naturally a central extension of G, in such a way that the projection
- π: G* → G
is a group homomorphism, and surjective. (The group structure on G* depends on the choice of an identity element mapping to the identity in G.) For example, when G* is the universal cover of G, the kernel of π is the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of G, which is known to be abelian (see H-space
H-space
In mathematics, an H-space is a topological space X together with a continuous map μ : X × X → X with an identity element e so that μ = μ = x for all x in X...
). Conversely, given a Lie group G and a discrete central subgroup Z, the quotient G/Z is a Lie group and G is a covering space of it.
More generally, when the groups A, E and G occurring in a central extension are Lie groups, and the maps between them are homomorphism of Lie groups, then the Lie algebra of E is a central extension of the Lie algebra of G by the Lie algebra of A. In the terminology of theoretical physics
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, generators of Lie(A) are called central charge
Central charge
In theoretical physics, a central charge is an operator Z that commutes with all the other symmetry operators. The adjective "central" refers to the center of the symmetry group -- the subgroup of elements that commute with all other elements of the original group—or to the center of a Lie algebra...
s. These generators are in the center of the Lie algebra of E; by Noether's theorem
Noether's theorem
Noether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...
, generators of symmetry groups correspond to conserved quantities, referred to as charges
Charge (physics)
In physics, a charge may refer to one of many different quantities, such as the electric charge in electromagnetism or the color charge in quantum chromodynamics. Charges are associated with conserved quantum numbers.-Formal definition:...
.
The basic examples of central extensions as covering groups are:
- the spin groups, which double cover the special orthogonal groups, which (in even dimension) double-cover the projective orthogonal groupProjective orthogonal groupIn projective geometry and linear algebra, the projective orthogonal group PO is the induced action of the orthogonal group of a quadratic space V = A quadratic space is a vector space V together with a quadratic form Q; the Q is dropped from notation when it is clear. on the associated projective...
. - the metaplectic groupMetaplectic groupIn mathematics, the metaplectic group Mp2n is a double cover of the symplectic group Sp2n. It can be defined over either real or p-adic numbers...
s, which double cover the symplectic groupSymplectic groupIn mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...
s.
The case of SL2(R) involves a fundamental group that is infinite cyclic. Here the central extension involved is well known in modular form
Modular form
In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
theory, in the case of forms of weight ½. A projective representation that corresponds is the Weil representation, constructed from the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
, in this case on the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
. Metaplectic groups also occur in quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
.
See also
- Algebraic extensionAlgebraic extensionIn abstract algebra, a field extension L/K is called algebraic if every element of L is algebraic over K, i.e. if every element of L is a root of some non-zero polynomial with coefficients in K. Field extensions that are not algebraic, i.e...
- Field extensionField extensionIn abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
- Ring extensionRing extensionIn mathematics, more specifically in ring theory, a ring extension or extension ring is a ring R with a subring S. We write R/S and say R is a ring extension of S...
- Group cohomologyGroup cohomologyIn abstract algebra, homological algebra, algebraic topology and algebraic number theory, as well as in applications to group theory proper, group cohomology is a way to study groups using a sequence of functors H n. The study of fixed points of groups acting on modules and quotient modules...
- Virasoro algebraVirasoro algebraIn mathematics, the Virasoro algebra is a complex Lie algebra, given as a central extension of the complex polynomial vector fields on the circle, and is widely used in conformal field theory and string theory....
- HNN extensionHNN extensionIn mathematics, the HNN extension is a basic construction of combinatorial group theory.Introduced in a 1949 paper Embedding Theorems for Groups by Graham Higman, B. H...

