
Linear complex structure
Encyclopedia
In mathematics
, a complex structure on a real vector space V is an automorphism
of V that squares to the minus identity
, −I. Such a structure on V allows one to define multiplication by complex scalars
in a canonical fashion so as to regard V as a complex vector space.
Complex structures have applications in representation theory
as well as in complex geometry
where they play an essential role in the definition of almost complex manifold
s, and the term "complex structure" often refers to this structure on manifolds; when it refers instead to a structure on vector spaces, it may be called a "linear complex structure".
such that
Here J2 means J composed
with itself and idV is the identity map
on V. That is, the effect of applying J twice is the same as multiplication by −1. This is reminiscent of multiplication by the imaginary unit, i
. A complex structure allows one to endow V with the structure of a complex vector space
. Complex scalar multiplication can be defined byv = xv + yJ(v)
for all real numbers x,y and all vectors v in V. One can check that this does, in fact, give V the structure of a complex vector space which we denote V J.
Going in the other direction, if one starts with a complex vector space W then one can define a complex structure on the underlying real space by defining Jw = i w for all w in W.
More formally, a linear complex structure on a real vector space is an algebra representation of the complex number
s C, thought of as an associative algebra
over the real number
s. This algebra is realized concretely as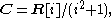 which corresponds to
which corresponds to 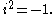 Then a representation of C is a real vector space V, together with an action of C on V (a map
Then a representation of C is a real vector space V, together with an action of C on V (a map 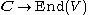 ). Concretely, this is just an action of i, as this generates the algebra, and the operator representing i (the image of i in End(V)) is exactly J.
). Concretely, this is just an action of i, as this generates the algebra, and the operator representing i (the image of i in End(V)) is exactly J.
If V J has complex dimension n then V must have real dimension 2n. That is, a finite-dimensional space V admits a complex structure only if it is even-dimensional. It is not hard to see that every even-dimensional vector space admits a complex structure. One can define J on pairs e,f of basis
vectors by Je = f and Jf = −e and then extend by linearity to all of V. If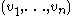 is a basis for the complex vector space V J then
is a basis for the complex vector space V J then  is a basis for the underlying real space V.
is a basis for the underlying real space V.
A real linear transformation A : V → V is a complex linear transformation of the corresponding complex space V J if and only if
A commutes with J, i.e.
Likewise, a real subspace
U of V is a complex subspace of V J if and only if J preserves U, i.e.
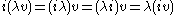 – and distributes across vector addition. As a complex n×n matrix, this is simply the scalar matrix with i on the diagonal. The corresponding real 2n×2n matrix is denoted J.
– and distributes across vector addition. As a complex n×n matrix, this is simply the scalar matrix with i on the diagonal. The corresponding real 2n×2n matrix is denoted J.
Given a basis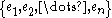 for the complex space, this set, together with these vectors multiplied by i, namely
for the complex space, this set, together with these vectors multiplied by i, namely 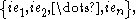 form a basis for the real space. There are two natural ways to order this basis, corresponding abstractly to whether one writes the tensor product as
form a basis for the real space. There are two natural ways to order this basis, corresponding abstractly to whether one writes the tensor product as  or instead as
or instead as 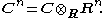
If one orders the basis as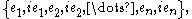 then the matrix for J takes the block diagonal form (subscripts added to indicate dimension):
then the matrix for J takes the block diagonal form (subscripts added to indicate dimension):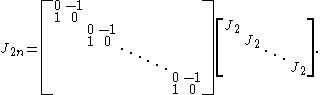
This ordering has the advantage that it respects direct sums, meaning that the basis for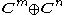 is the same as that for
is the same as that for 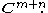
Conversely, if one orders the basis as then the matrix for J is block-antidiagonal:
then the matrix for J is block-antidiagonal:
This ordering is more natural if one thinks of the real space as a direct sum, as discussed below.
The data of the real vector space and the J matrix is exactly the same as the data of the complex vector space, as the J matrix allows one to define complex multiplication. At the level of Lie algebra
s and Lie group
s, this corresponds to the inclusion of gl(n,C) in gl(2n,R) (Lie algebras – matrices, not necessarily invertible) and GL(n,C) in GL(2n,R):
The inclusion corresponds to forgetting the complex structure (and keeping only the real), while the subgroup GL(n,C) can be characterized (given in equations) as the matrices that commute with J:
The corresponding statement about Lie algebras is that the subalgebra gl(n,C) of complex matrices are those whose Lie bracket
with J vanishes, meaning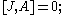 in other words, as the kernel of the map of bracketing with J,
in other words, as the kernel of the map of bracketing with J, 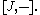
Note that the defining equations for these statements are the same, as AJ = JA is the same as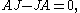 which is the same as
which is the same as 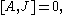 though the meaning of the Lie bracket vanishing is less immediate geometrically than the meaning of commuting.
though the meaning of the Lie bracket vanishing is less immediate geometrically than the meaning of commuting.
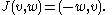
The block matrix
form of J is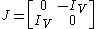
where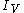 is the identity map on V. This corresponds to the complex structure on the tensor product
is the identity map on V. This corresponds to the complex structure on the tensor product 
for all u,v in V. An equivalent characterization is that J is skew-adjoint with respect to B:
If g is an inner product on V then J preserves g if and only if J is an orthogonal transformation. Likewise, J preserves a nondegenerate, skew-symmetric form ω if and only if J is a symplectic transformation (that is, if ω(Ju,Jv) = ω(u,v)). For symplectic forms ω there is usually an added restriction for compatibility between J and ω, namely
for all u in V. If this condition is satisfied then J is said to tame ω.
Given a symplectic form ω and a linear complex structure J, one may define an associated symmetric bilinear form gJ on VJ
Because a symplectic form is nondegenerate, so is the associated bilinear form. Moreover, the associated form is preserved by J if and only if the symplectic form and if ω is tamed by J then the associated form is positive definite. Thus in this case the associated form is a Hermitian form and VJ is an inner product space
.
by extension of scalars
: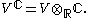
This is a complex vector space whose complex dimension is equal to the real dimension of V. It has a canonical complex conjugation defined by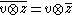
If J is a complex structure on V, we may extend J by linearity to VC:
Since C is algebraically closed, J is guaranteed to have eigenvalues which satisfy λ2 = −1, namely λ = ±i. Thus we may write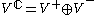
where V+ and V− are the eigenspaces of +i and −i, respectively. Complex conjugation interchanges V+ and V−. The projection maps onto the V± eigenspaces are given by
So that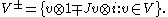
There is a natural complex linear isomorphism between VJ and V+, so these vector spaces can be considered the same, while V− may be regarded as the complex conjugate
of VJ.
Note that if VJ has complex dimension n then both V+ and V− have complex dimension n while VC has complex dimension 2n.
Abstractly, if one starts with a complex vector space W and takes the complexification of the underlying real space, one obtains a space isomorphic to the direct sum of W and its conjugate: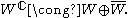
V* has a natural complex structure J* given by the dual (or transpose
) of J. The complexification of the dual space (V*)C therefore has a natural decomposition
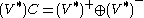
into the ±i eigenspaces of J*. Under the natural identification of (V*)C with (VC)* one can characterize (V*)+ as those complex linear functionals which vanish on V−. Likewise (V*)− consists of those complex linear functionals which vanish on V+.
The (complex) tensor
, symmetric
, and exterior algebra
s over VC also admit decompositions. The exterior algebra is perhaps the most important application of this decomposition. In general, if a vector space U admits a decompositon U = S ⊕ T then the exterior powers of U can be decomposed as follows: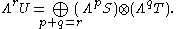
A complex structure J on V therefore induces a decomposition
where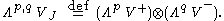
All exterior powers are taken over the complex numbers. So if VJ is has complex dimension n (real dimension 2n) then
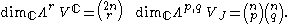
The dimensions add up correctly as a consequence of Vandermonde's identity.
The space of (p,q)-forms Λp,q VJ* is the space of (complex) multilinear forms on VC which vanish on homogeneous elements unless p are from V+ and q are from V−. It is also possible to regard Λp,q VJ* as the space of real multilinear maps from VJ to C which are complex linear in p terms and conjugate-linear in q terms.
See complex differential form
and almost complex manifold
for applications of these ideas.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a complex structure on a real vector space V is an automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
of V that squares to the minus identity
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
, −I. Such a structure on V allows one to define multiplication by complex scalars
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
in a canonical fashion so as to regard V as a complex vector space.
Complex structures have applications in representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
as well as in complex geometry
Complex geometry
In mathematics, complex geometry is the study of complex manifolds and functions of many complex variables. Application of transcendental methods to algebraic geometry falls in this category, together with more geometric chapters of complex analysis....
where they play an essential role in the definition of almost complex manifold
Almost complex manifold
In mathematics, an almost complex manifold is a smooth manifold equipped with smooth linear complex structure on each tangent space. The existence of this structure is a necessary, but not sufficient, condition for a manifold to be a complex manifold. That is, every complex manifold is an almost...
s, and the term "complex structure" often refers to this structure on manifolds; when it refers instead to a structure on vector spaces, it may be called a "linear complex structure".
Definition and properties
A complex structure on a real vector space V is a real linear transformationLinear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
- J : V → V
such that
- J2 = −idV.
Here J2 means J composed
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
with itself and idV is the identity map
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
on V. That is, the effect of applying J twice is the same as multiplication by −1. This is reminiscent of multiplication by the imaginary unit, i
Imaginary unit
In mathematics, the imaginary unit allows the real number system ℝ to be extended to the complex number system ℂ, which in turn provides at least one root for every polynomial . The imaginary unit is denoted by , , or the Greek...
. A complex structure allows one to endow V with the structure of a complex vector space
Complex vector space
A complex vector space is a vector space over the complex numbers. It can also refer to:* a vector space over the real numbers with a linear complex structure...
. Complex scalar multiplication can be defined byv = xv + yJ(v)
for all real numbers x,y and all vectors v in V. One can check that this does, in fact, give V the structure of a complex vector space which we denote V J.
Going in the other direction, if one starts with a complex vector space W then one can define a complex structure on the underlying real space by defining Jw = i w for all w in W.
More formally, a linear complex structure on a real vector space is an algebra representation of the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s C, thought of as an associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
over the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. This algebra is realized concretely as
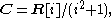 which corresponds to
which corresponds to 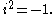 Then a representation of C is a real vector space V, together with an action of C on V (a map
Then a representation of C is a real vector space V, together with an action of C on V (a map 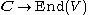 ). Concretely, this is just an action of i, as this generates the algebra, and the operator representing i (the image of i in End(V)) is exactly J.
). Concretely, this is just an action of i, as this generates the algebra, and the operator representing i (the image of i in End(V)) is exactly J.If V J has complex dimension n then V must have real dimension 2n. That is, a finite-dimensional space V admits a complex structure only if it is even-dimensional. It is not hard to see that every even-dimensional vector space admits a complex structure. One can define J on pairs e,f of basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
vectors by Je = f and Jf = −e and then extend by linearity to all of V. If
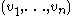 is a basis for the complex vector space V J then
is a basis for the complex vector space V J then  is a basis for the underlying real space V.
is a basis for the underlying real space V.A real linear transformation A : V → V is a complex linear transformation of the corresponding complex space V J if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
A commutes with J, i.e.
- AJ = JA
Likewise, a real subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
U of V is a complex subspace of V J if and only if J preserves U, i.e.
- JU = U
Cn
The fundamental example of a linear complex structure is the structure on R2n coming from the complex structure on Cn. That is, the complex n-dimensional space Cn is also a real 2n-dimensional space – using the same vector addition and real scalar multiplication – while multiplication by the complex number i is not only a complex linear transform of the space, thought of as a complex vector space, but also a real linear transform of the space, thought of as a real vector space. Concretely, this is because scalar multiplication by i commutes with scalar multiplication by real numbers –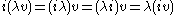 – and distributes across vector addition. As a complex n×n matrix, this is simply the scalar matrix with i on the diagonal. The corresponding real 2n×2n matrix is denoted J.
– and distributes across vector addition. As a complex n×n matrix, this is simply the scalar matrix with i on the diagonal. The corresponding real 2n×2n matrix is denoted J.Given a basis
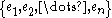 for the complex space, this set, together with these vectors multiplied by i, namely
for the complex space, this set, together with these vectors multiplied by i, namely 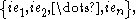 form a basis for the real space. There are two natural ways to order this basis, corresponding abstractly to whether one writes the tensor product as
form a basis for the real space. There are two natural ways to order this basis, corresponding abstractly to whether one writes the tensor product as  or instead as
or instead as 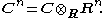
If one orders the basis as
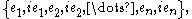 then the matrix for J takes the block diagonal form (subscripts added to indicate dimension):
then the matrix for J takes the block diagonal form (subscripts added to indicate dimension):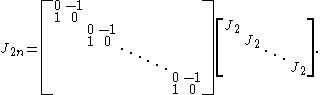
This ordering has the advantage that it respects direct sums, meaning that the basis for
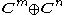 is the same as that for
is the same as that for 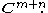
Conversely, if one orders the basis as
 then the matrix for J is block-antidiagonal:
then the matrix for J is block-antidiagonal:
This ordering is more natural if one thinks of the real space as a direct sum, as discussed below.
The data of the real vector space and the J matrix is exactly the same as the data of the complex vector space, as the J matrix allows one to define complex multiplication. At the level of Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s and Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s, this corresponds to the inclusion of gl(n,C) in gl(2n,R) (Lie algebras – matrices, not necessarily invertible) and GL(n,C) in GL(2n,R):
- gl(n,C) < gl(2n,R) and GL(n,C) < GL(2n,R).
The inclusion corresponds to forgetting the complex structure (and keeping only the real), while the subgroup GL(n,C) can be characterized (given in equations) as the matrices that commute with J:
- GL(n,C) =

The corresponding statement about Lie algebras is that the subalgebra gl(n,C) of complex matrices are those whose Lie bracket
Lie bracket
Lie bracket can refer to:*A bilinear binary operation defined on elements of a Lie algebra*Lie bracket of vector fields...
with J vanishes, meaning
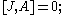 in other words, as the kernel of the map of bracketing with J,
in other words, as the kernel of the map of bracketing with J, 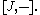
Note that the defining equations for these statements are the same, as AJ = JA is the same as
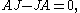 which is the same as
which is the same as 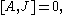 though the meaning of the Lie bracket vanishing is less immediate geometrically than the meaning of commuting.
though the meaning of the Lie bracket vanishing is less immediate geometrically than the meaning of commuting.Direct sum
If V is any real vector space there is a canonical complex structure on the direct sum V ⊕ V given by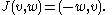
The block matrix
Block matrix
In the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle...
form of J is
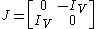
where
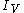 is the identity map on V. This corresponds to the complex structure on the tensor product
is the identity map on V. This corresponds to the complex structure on the tensor product 
Compatibility with other structures
If B is a bilinear form on V then we say that J preserves B if- B(Ju, Jv) = B(u, v)
for all u,v in V. An equivalent characterization is that J is skew-adjoint with respect to B:
- B(Ju, v) = −B(u, Jv)
If g is an inner product on V then J preserves g if and only if J is an orthogonal transformation. Likewise, J preserves a nondegenerate, skew-symmetric form ω if and only if J is a symplectic transformation (that is, if ω(Ju,Jv) = ω(u,v)). For symplectic forms ω there is usually an added restriction for compatibility between J and ω, namely
- ω(u, Ju) > 0
for all u in V. If this condition is satisfied then J is said to tame ω.
Given a symplectic form ω and a linear complex structure J, one may define an associated symmetric bilinear form gJ on VJ
- gJ(u,v) = ω(u,Jv).
Because a symplectic form is nondegenerate, so is the associated bilinear form. Moreover, the associated form is preserved by J if and only if the symplectic form and if ω is tamed by J then the associated form is positive definite. Thus in this case the associated form is a Hermitian form and VJ is an inner product space
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
.
Relation to complexifications
Given any real vector space V we may define its complexificationComplexification
In mathematics, the complexification of a real vector space V is a vector space VC over the complex number field obtained by formally extending scalar multiplication to include multiplication by complex numbers. Any basis for V over the real numbers serves as a basis for VC over the complex...
by extension of scalars
Extension of scalars
In abstract algebra, extension of scalars is a means of producing a module over a ring S from a module over another ring R, given a homomorphism f : R \to S between them...
:
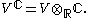
This is a complex vector space whose complex dimension is equal to the real dimension of V. It has a canonical complex conjugation defined by
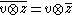
If J is a complex structure on V, we may extend J by linearity to VC:

Since C is algebraically closed, J is guaranteed to have eigenvalues which satisfy λ2 = −1, namely λ = ±i. Thus we may write
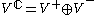
where V+ and V− are the eigenspaces of +i and −i, respectively. Complex conjugation interchanges V+ and V−. The projection maps onto the V± eigenspaces are given by

So that
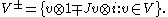
There is a natural complex linear isomorphism between VJ and V+, so these vector spaces can be considered the same, while V− may be regarded as the complex conjugate
Complex conjugate vector space
In mathematics, the complex conjugate of a complex vector space V\, is the complex vector space \overline V consisting of all formal complex conjugates of elements of V\,...
of VJ.
Note that if VJ has complex dimension n then both V+ and V− have complex dimension n while VC has complex dimension 2n.
Abstractly, if one starts with a complex vector space W and takes the complexification of the underlying real space, one obtains a space isomorphic to the direct sum of W and its conjugate:
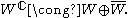
Extension to related vector spaces
Let V be a real vector space with a complex structure J. The dual spaceDual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
V* has a natural complex structure J* given by the dual (or transpose
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
) of J. The complexification of the dual space (V*)C therefore has a natural decomposition
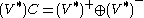
into the ±i eigenspaces of J*. Under the natural identification of (V*)C with (VC)* one can characterize (V*)+ as those complex linear functionals which vanish on V−. Likewise (V*)− consists of those complex linear functionals which vanish on V+.
The (complex) tensor
Tensor algebra
In mathematics, the tensor algebra of a vector space V, denoted T or T•, is the algebra of tensors on V with multiplication being the tensor product...
, symmetric
Symmetric algebra
In mathematics, the symmetric algebra S on a vector space V over a field K is the free commutative unital associative algebra over K containing V....
, and exterior algebra
Exterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
s over VC also admit decompositions. The exterior algebra is perhaps the most important application of this decomposition. In general, if a vector space U admits a decompositon U = S ⊕ T then the exterior powers of U can be decomposed as follows:
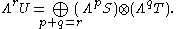
A complex structure J on V therefore induces a decomposition

where
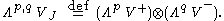
All exterior powers are taken over the complex numbers. So if VJ is has complex dimension n (real dimension 2n) then
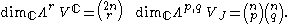
The dimensions add up correctly as a consequence of Vandermonde's identity.
The space of (p,q)-forms Λp,q VJ* is the space of (complex) multilinear forms on VC which vanish on homogeneous elements unless p are from V+ and q are from V−. It is also possible to regard Λp,q VJ* as the space of real multilinear maps from VJ to C which are complex linear in p terms and conjugate-linear in q terms.
See complex differential form
Complex differential form
In mathematics, a complex differential form is a differential form on a manifold which is permitted to have complex coefficients....
and almost complex manifold
Almost complex manifold
In mathematics, an almost complex manifold is a smooth manifold equipped with smooth linear complex structure on each tangent space. The existence of this structure is a necessary, but not sufficient, condition for a manifold to be a complex manifold. That is, every complex manifold is an almost...
for applications of these ideas.
See also
- Almost complex manifoldAlmost complex manifoldIn mathematics, an almost complex manifold is a smooth manifold equipped with smooth linear complex structure on each tangent space. The existence of this structure is a necessary, but not sufficient, condition for a manifold to be a complex manifold. That is, every complex manifold is an almost...
- Complex manifoldComplex manifoldIn differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
- Complex differential formComplex differential formIn mathematics, a complex differential form is a differential form on a manifold which is permitted to have complex coefficients....
- Complex conjugate vector spaceComplex conjugate vector spaceIn mathematics, the complex conjugate of a complex vector space V\, is the complex vector space \overline V consisting of all formal complex conjugates of elements of V\,...
- Hermitian structure
- Real structureReal structureIn mathematics, a real structure on a complex vector space is a way to decompose the complex vector space in the direct sum of two real vector spaces...

