
Fano plane
Encyclopedia
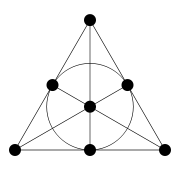
Finite geometry
A finite geometry is any geometric system that has only a finite number of points.Euclidean geometry, for example, is not finite, because a Euclidean line contains infinitely many points, in fact as many points as there are real numbers...
, the Fano plane (after Gino Fano
Gino Fano
Gino Fano was an Italian mathematician. He was born in Mantua, Italy and died in Verona, Italy.Fano worked on projective and algebraic geometry; the Fano plane, Fano fibration, Fano surface, and Fano varieties are named for him....
) is the finite
Finite geometry
A finite geometry is any geometric system that has only a finite number of points.Euclidean geometry, for example, is not finite, because a Euclidean line contains infinitely many points, in fact as many points as there are real numbers...
projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
with the smallest possible number of points and lines: 7 each.
Homogeneous coordinates
The Fano plane can be constructed via linear algebraLinear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
as the projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
over the finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
with two elements. One can similarly define projective planes over any other finite field, with the Fano plane being the smallest.
Using the standard construction of projective spaces via homogeneous coordinates
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
, the seven points of the Fano plane may be labeled with the seven non-zero ordered triples of binary digits 001, 010, 011, 100, 101, 110, and 111. This can be done in such a way that for every two points p and q, the third point on line pq has the label formed by adding the labels of p and q modulo 2. In other words, the points of the Fano plane correspond to the non-zero points of the finite vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of dimension 3 over the finite field of order 2.
The lines of the Fano plane may also be given homogeneous coordinates, again using non-zero triples of binary digits. With this system of coordinates, a point is incident to a line if the coordinate for the point and the coordinate for the line have an even number of positions at which they both have nonzero bits: for instance, the point 101 belongs to the line 111, because they have nonzero bits at two common positions. In terms of the underlying linear algebra, a point belongs to a line if the inner product of the vectors representing the point and line is zero.
The lines can be classified into three types.
- On three of the lines the binary codes for the points have the 0 in a constant position: the line 100 (containing the points 001, 010, and 011) has 0 in the first position, and the lines 010 and 001 are formed in the same way.
- On three of the lines, two of the positions in the binary codes of each point have the same value: in the line 110 (containing the points 001, 110, and 111) the first and second positions are always equal, and the lines 101 and 011 are formed in the same way.
- In the remaining line 111 (containing the points 011, 101, and 110), each binary code has exactly two nonzero bits.
Symmetries
A permutation of the seven points of the Fano plane that carries collinearIncidence (geometry)
In geometry, the relations of incidence are those such as 'lies on' between points and lines , and 'intersects' . That is, they are the binary relations describing how subsets meet...
points (points on the same line) to collinear points (in other words, it "preserves collinearity") is called a "collineation
Collineation
In projective geometry, a collineation is a one-to-one and onto map from one projective space to another, or from a projective space to itself, such that the images of collinear points are themselves collinear. All projective linear transformations induce a collineation...
", "automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
", or "symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
" of the plane. The full collineation group
Collineation
In projective geometry, a collineation is a one-to-one and onto map from one projective space to another, or from a projective space to itself, such that the images of collinear points are themselves collinear. All projective linear transformations induce a collineation...
(or automorphism group, or symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
) is isomorphic to the projective special linear group PSL(2,7)
PSL(2,7)
In mathematics, the projective special linear group PSL is a finite simple group that has important applications in algebra, geometry, and number theory. It is the automorphism group of the Klein quartic as well as the symmetry group of the Fano plane...
= PSL(3,2), and the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
GL(3,2) (which is equal to PSL(3,2) because the field has only one nonzero element). It consists of 168 different permutations.
The automorphism group is made up of 6 conjugacy classes.
All cycle structures except the 7-cycle uniquely define a conjugacy class:
- The identity permutation
- 21 permutations with two 2-cycles
- 42 permutations with a 4-cycle and a 2-cycle
- 56 permutations with two 3-cycles
The 48 permutations with a complete 7-cycle form two distinct conjugacy classes with 24 elements:
- A maps to B, B to C, C to D. Than D is on the same line as A and B.
- A maps to B, B to C, C to D. Than D is on the same line as A and C.
See Fano plane collineations for a complete list.
Configurations
The Fano plane contains the following numbers of configurations of points and lines of different types. For each type of configuration, the number of copies of configuration multiplied by the number of symmetries of the plane that keep the configuration unchanged is equal to 168, the size of the entire symmetry group.- There are 7 points, and 24 symmetries fixing any point.
- There are 7 lines, and 24 symmetries fixing any line.
- There are 21 unordered pairs of points, each of which may be mapped by a symmetry onto any other unordered pair. For any unordered pair there are 8 symmetries fixing it.
- There are 21 flags consisting of a line and a point on that line. Each flag corresponds to the unordered pair of the other two points on the same line. For each flag, 8 different symmetries keep it fixed.
- There are 21 ways of selecting a quadrangleQuadrangleQuadrangle may refer to :*Quadrangle , a courtyard surrounded by a building or several buildings.*The Quadrangle, a group of five museums in Springfield, Massachusetts, including the United States' first planetarium and the Dr...
of four cyclically ordered points no three of which are collinear, and eight symmetries that fix any such quadrangle. For each flag consisting of a point p and a line l, there is a unique quadrangle in which the four points of the quadrangle are disjoint from l and the four edges of the quadrangle do not pass through p, and every quadrangle corresponds to a flag in this way. - There are 28 triangleTriangleA triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
s, which correspond one-for-one with the 28 bitangents of a quartic . For each triangle there are six symmetries fixing it, one for each permutation of the points within the triangle. - There are 28 ways of selecting a point and a line that are not incident to each other, and six ways of permuting the Fano plane while keeping a configuration of this type fixed. For every non-incident point-line pair (p,l), the three points that are unequal to p and that do not belong to l form a triangle, and for every triangle there is a unique way of grouping the remaining four points into a non-incident point-line pair.
- There are 28 ways of specifying a hexagon in which no three consecutive vertices lie on a line, and six symmetries fixing any such hexagon.
- There are 42 ordered pairOrdered pairIn mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
s of points, and again each may be mapped by a symmetry onto any other ordered pair. For any ordered pair there are 4 symmetries fixing it. - There are 84 ways of specifying a triangle together with one point on that triangle, each of which has two symmetries fixing it.
- There are 84 ways of specifying a pentagonPentagonIn geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
in which no three consecutive vertices lie on a line, and two symmetries fixing any pentagon. - There are 168 different ways of specifying a triangle together with an ordering for its three points, and only the identity symmetry fixes this configuration.
Group-theoretic construction
Alternatively, the 7 points of the plane correspond to the 7 non-identity elements of the groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
(Z2)3 = Z2 × Z2 × Z2. The lines of the plane correspond to the subgroups of order 4, isomorphic to Z2 × Z2. The automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
group of the group (Z2)3 is that of the Fano plane, and has order 168.
Block design theory
The Fano plane is a small symmetricSymmetric design
In combinatorial mathematics, a symmetric design is a block design with equal numbers of points and blocks. Thus, it has the fewest possible blocks given the number of points . They are also known as projective designs....
block design, specifically a 2-(7,3,1)-design. The points of the design are the points of the plane, and the blocks of the design are the lines of the plane. As such it is a valuable example in (block) design theory.
Matroid theory
- Main article: Matroid theory
The Fano plane is one of the important examples in the structure theory of matroid
Matroid
In combinatorics, a branch of mathematics, a matroid or independence structure is a structure that captures the essence of a notion of "independence" that generalizes linear independence in vector spaces....
s. Excluding the Fano plane as a minor
Matroid
In combinatorics, a branch of mathematics, a matroid or independence structure is a structure that captures the essence of a notion of "independence" that generalizes linear independence in vector spaces....
is necessary to characterize several important classes of matroids, such as regular, graphic, and cographic ones.
Discrete Geometry
If you remove one particular line you obtain the "failed Fano configuration", which can be embedded in the real plane. It is one of the important examples in discrete geometry and must be excluded for many theorems to hold.Steiner system
The Fano plane can be given the structure of a quasigroupQuasigroup
In mathematics, especially in abstract algebra, a quasigroup is an algebraic structure resembling a group in the sense that "division" is always possible...
making it a Steiner triple system. The quasigroup coincides precisely with the multiplicative structure defined by the unit octonion
Octonion
In mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H...
s e1, e2, ..., e7 .
See also
- Incidence structureIncidence structureIn mathematics, an incidence structure is a tripleC=.\,where P is a set of "points", L is a set of "lines" and I \subseteq P \times L is the incidence relation. The elements of I are called flags. If \in I,...
- Projective geometryProjective geometryIn mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
- Projective configuration
- Projective planeProjective planeIn mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...

