
Affine group
Overview
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the affine group or general affine group of any affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K is the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of all invertible affine transformation
Affine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
s from the space into itself.
It is a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
if K is the real or complex field or quaternions.
Concretely, given a vector space V, it has an underlying affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
A obtained by “forgetting” the origin, with V acting by translations, and the affine group of A can be described concretely as the semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of V by GL(V), the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
of V:
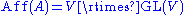
The action of GL(V) on V is the natural one (linear transformations are automorphisms), so this defines a semidirect product.
In terms of matrices, one writes:
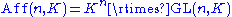
where here the natural action of GL(n,K) on Kn is matrix multiplication of a vector.
Given the affine group of an affine space A, the stabilizer of a point p is isomorphic to the general linear group of the same dimension (so the stabilizer of a point in Aff(2,R) is isomorphic to GL(2,R)); formally, it is the general linear group of the vector space
 : recall that if one fixes a point, an affine space becomes a vector space.
: recall that if one fixes a point, an affine space becomes a vector space.All these subgroups are conjugate, where conjugation is given by translation from p to q (which is uniquely defined), however, no particular subgroup is a natural choice, since no point is special – this corresponds to the multiple choices of transverse subgroup, or splitting of the short exact sequence
 .
.In the case that the affine group was constructed by starting with a vector space, the subgroup that stabilizes the origin (of the vector space) is the original GL(V).
Representing the affine group as a semidirect product of V by GL(V), then by construction of the semidirect product, the elements are pairs (M, v), where v is a vector in V and M is a linear transform in GL(V), and multiplication is given by:
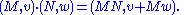
This can be represented as the (n + 1)×(n + 1) block matrix
Block matrix
In the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle...
:
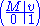
where M is an n×n matrix over K, v an n × 1 column vector, 0 is a 1 × n row of zeros, and 1 is the 1 × 1 identity block matrix.
Formally, Aff(V) is naturally isomorphic to a subgroup of
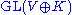 , with V embedded as the affine plane
, with V embedded as the affine plane 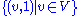 , namely the stabilizer of this affine plane; the above matrix formulation is the (transpose of) the realization of this, with the (n × n and 1 × 1) blocks corresponding to the direct sum decomposition
, namely the stabilizer of this affine plane; the above matrix formulation is the (transpose of) the realization of this, with the (n × n and 1 × 1) blocks corresponding to the direct sum decomposition 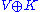 .
.A similar representation is any (n + 1)×(n + 1) matrix in which the entries in each column sum to 1.
Unanswered Questions

