Sign (mathematics)
Encyclopedia
In mathematics
, the word sign refers to the property of being positive or negative. Every nonzero real number
is either positive or negative, and therefore has a sign. Zero
itself is signless, although in some contexts it makes sense to consider a signed zero. In addition to its application to real numbers, the word sign is used throughout mathematics to indicate aspects of mathematical objects that resemble positivity and negativity, such as the sign of a permutation.
The word sign is also sometimes used to refer to various mathematical symbol
s, such as the plus and minus symbols
and the multiplication symbol. See the table of mathematical symbols
for more information on signs and symbols in mathematics.
is said to be positive if it is greater than zero, and negative if it is less than zero. The attribute of being positive or negative is called the sign of the number. Zero itself is not considered to have a sign.
In arithmetic
, the sign of a number is often denoted by placing a plus or minus sign before the number. For example, +3 would denote a positive 3, and −3 would denote a negative 3. When no plus or minus sign is given, the default interpretation is that a number is positive.
In algebra
, a minus sign is usually thought of as representing the operation of negation
, with the negation of a positive number being negative and the negation of a negative number being positive. In this context, it makes sense to write −(−3) = +3.
The sign of any nonzero number can be changed to positive using the absolute value
function. For example, the absolute value of −3 and the absolute value of 3 are both equal to 3. In symbols, this would be written |−3| = 3 and |3| = 3.
is neither positive nor negative, and therefore has no sign. In arithmetic, +0 and −0 both denote the same number 0, and the negation
of zero is zero itself.
In some contexts, such as signed number representations
in computing
, it makes sense to consider signed versions of zero, with positive zero and negative zero being different numbers (see signed zero).
One also sees +0 and −0 in calculus
and mathematical analysis
when evaluating certain limit
s. This notation refers to the behaviour of a function as the input variable approaches 0 from positive or negative values respectively; these behaviours are not necessarily the same.
Thus a non-negative number is either positive or zero, while a non-positive number is either negative or zero. For example, the absolute value
of a real number is always non-negative, but is not necessarily positive.
The same terminology is sometimes used for functions
that take real or integer values. For example, a function would be called positive if all of its values are positive, or non-negative if all of its values are non-negative.
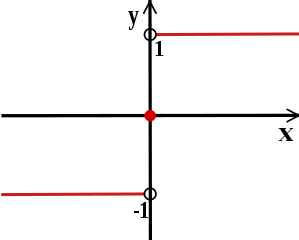
The sign function or signum function is sometimes used to extract the sign of a number. This function is usually defined as follows: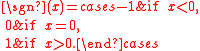
Thus sgn(x) is 1 when x is positive, and sgn(x) is −1 when x is negative. For nonzero values of x, this function can also be defined by the formula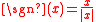
where |x| is the absolute value
of x.
, particularly an oriented angle or an angle of rotation
. In such a situation, the sign indicates whether the angle is in the clockwise
or counterclockwise direction. Though different conventions can be used, it is common in mathematics
to have counterclockwise angles count as positive, and clockwise angles count as negative.
It is also possible to associate a sign to an angle of rotation in three dimensions, assuming the axis of rotation has been oriented. Specifically, a right-handed
rotation around an oriented axis typically counts as positive, while a left-handed rotation counts as negative.
in the value of x is typically defined by the equation
Using this convention, an increase in x counts as positive change, while a decrease of x counts as negative change. In calculus
, this same convention is used in the definition of the derivative
. As a result, any increasing function
has positive derivative, while a decreasing function has negative derivative.
and physics
, it is common to label certain directions as positive or negative. For a basic example, the number line
is usually drawn with positive numbers to the right, and negative numbers to the left:
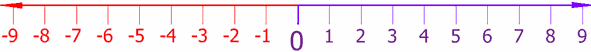As a result, when discussing linear motion
, displacement
or velocity
to the right is usually thought of as being positive, while similar motion to the left is thought of as being negative.
On the Cartesian plane, the rightward and upward directions are usually thought of as positive, with rightward being the positive x-direction, and upward being the positive y-direction. If a displacement or velocity vector is separated into its vector components, then the horizontal part will be positive for motion to the right and negative for motion to the left, while the vertical part will be positive for motion upward and negative for motion downward.
, a numeric value may be either signed or unsigned, depending on whether the computer is keeping track of a sign for the number. By restricting a variable
to non-negative values only, one more bit
can be used for storing the value of a number.
Because of the way arithmetic is done within computers, the sign of a signed variable is usually not stored as a single independent bit, but is instead stored using two's complement
or some other signed number representation.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the word sign refers to the property of being positive or negative. Every nonzero real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
is either positive or negative, and therefore has a sign. Zero
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
itself is signless, although in some contexts it makes sense to consider a signed zero. In addition to its application to real numbers, the word sign is used throughout mathematics to indicate aspects of mathematical objects that resemble positivity and negativity, such as the sign of a permutation.
The word sign is also sometimes used to refer to various mathematical symbol
Symbol
A symbol is something which represents an idea, a physical entity or a process but is distinct from it. The purpose of a symbol is to communicate meaning. For example, a red octagon may be a symbol for "STOP". On a map, a picture of a tent might represent a campsite. Numerals are symbols for...
s, such as the plus and minus symbols
Plus and minus signs
The plus and minus signs are mathematical symbols used to represent the notions of positive and negative as well as the operations of addition and subtraction. Their use has been extended to many other meanings, more or less analogous...
and the multiplication symbol. See the table of mathematical symbols
Table of mathematical symbols
This is a listing of common symbols found within all branches of mathematics. Each symbol is listed in both HTML, which depends on appropriate fonts being installed, and in , as an image.-Symbols:-Variations:...
for more information on signs and symbols in mathematics.
Sign of a number
A real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
is said to be positive if it is greater than zero, and negative if it is less than zero. The attribute of being positive or negative is called the sign of the number. Zero itself is not considered to have a sign.
In arithmetic
Arithmetic
Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...
, the sign of a number is often denoted by placing a plus or minus sign before the number. For example, +3 would denote a positive 3, and −3 would denote a negative 3. When no plus or minus sign is given, the default interpretation is that a number is positive.
In algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, a minus sign is usually thought of as representing the operation of negation
Negation (algebra)
Negation is the mathematical operation that reverses the sign of a number. Thus the negation of a positive number is negative, and the negation of a negative number is positive. The negation of zero is zero...
, with the negation of a positive number being negative and the negation of a negative number being positive. In this context, it makes sense to write −(−3) = +3.
The sign of any nonzero number can be changed to positive using the absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
function. For example, the absolute value of −3 and the absolute value of 3 are both equal to 3. In symbols, this would be written |−3| = 3 and |3| = 3.
Sign of zero
The number zero0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
is neither positive nor negative, and therefore has no sign. In arithmetic, +0 and −0 both denote the same number 0, and the negation
Negation (algebra)
Negation is the mathematical operation that reverses the sign of a number. Thus the negation of a positive number is negative, and the negation of a negative number is positive. The negation of zero is zero...
of zero is zero itself.
In some contexts, such as signed number representations
Signed number representations
In computing, signed number representations are required to encode negative numbers in binary number systems.In mathematics, negative numbers in any base are represented by prefixing them with a − sign. However, in computer hardware, numbers are represented in binary only without extra...
in computing
Computing
Computing is usually defined as the activity of using and improving computer hardware and software. It is the computer-specific part of information technology...
, it makes sense to consider signed versions of zero, with positive zero and negative zero being different numbers (see signed zero).
One also sees +0 and −0 in calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
and mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
when evaluating certain limit
Limit
A limit can be:* Limit :** Limit of a function** Limit of a sequence** One-sided limit** Limit superior and limit inferior** Limit of a net** Limit point** Limit ** Direct limit and Inverse limit...
s. This notation refers to the behaviour of a function as the input variable approaches 0 from positive or negative values respectively; these behaviours are not necessarily the same.
Terminology for signs
Because zero is neither positive nor negative, the following phrases are sometimes used to refer to the sign of an unknown number:- A number is positive if it is greater than zero.
- A number is negative if it is less than zero.
- A number is non-negative if it is greater than or equal to zero.
- A number is non-positive if it is less than or equal to zero.
Thus a non-negative number is either positive or zero, while a non-positive number is either negative or zero. For example, the absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of a real number is always non-negative, but is not necessarily positive.
The same terminology is sometimes used for functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
that take real or integer values. For example, a function would be called positive if all of its values are positive, or non-negative if all of its values are non-negative.
Sign convention
In many contexts the choice of sign convention (which range of values is considered positive and which negative) is natural, whereas in others the choice is arbitrary subject only to consistency, the latter necessitating an explicit sign convention.Sign function
The sign function or signum function is sometimes used to extract the sign of a number. This function is usually defined as follows:
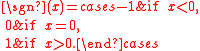
Thus sgn(x) is 1 when x is positive, and sgn(x) is −1 when x is negative. For nonzero values of x, this function can also be defined by the formula
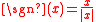
where |x| is the absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of x.
Sign of an angle
In many contexts, it is common to associate a sign with the measure of an angleAngle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
, particularly an oriented angle or an angle of rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
. In such a situation, the sign indicates whether the angle is in the clockwise
Clockwise
Circular motion can occur in two possible directions. A clockwise motion is one that proceeds in the same direction as a clock's hands: from the top to the right, then down and then to the left, and back to the top...
or counterclockwise direction. Though different conventions can be used, it is common in mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
to have counterclockwise angles count as positive, and clockwise angles count as negative.
It is also possible to associate a sign to an angle of rotation in three dimensions, assuming the axis of rotation has been oriented. Specifically, a right-handed
Right-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
rotation around an oriented axis typically counts as positive, while a left-handed rotation counts as negative.
Sign of a change
When a quantity x changes over time, the changeFinite difference
A finite difference is a mathematical expression of the form f − f. If a finite difference is divided by b − a, one gets a difference quotient...
in the value of x is typically defined by the equation
Using this convention, an increase in x counts as positive change, while a decrease of x counts as negative change. In calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, this same convention is used in the definition of the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
. As a result, any increasing function
Monotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
has positive derivative, while a decreasing function has negative derivative.
Sign of a direction
In analytic geometryAnalytic geometry
Analytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
and physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, it is common to label certain directions as positive or negative. For a basic example, the number line
Number line
In basic mathematics, a number line is a picture of a straight line on which every point is assumed to correspond to a real number and every real number to a point. Often the integers are shown as specially-marked points evenly spaced on the line...
is usually drawn with positive numbers to the right, and negative numbers to the left:
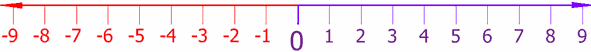
Linear motion
Linear motion is motion along a straight line, and can therefore be described mathematically using only one spatial dimension. The linear motion can be of two types: uniform linear motion, with constant velocity or zero acceleration; non uniform linear motion, with variable velocity or non-zero...
, displacement
Displacement (vector)
A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P...
or velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
to the right is usually thought of as being positive, while similar motion to the left is thought of as being negative.
On the Cartesian plane, the rightward and upward directions are usually thought of as positive, with rightward being the positive x-direction, and upward being the positive y-direction. If a displacement or velocity vector is separated into its vector components, then the horizontal part will be positive for motion to the right and negative for motion to the left, while the vertical part will be positive for motion upward and negative for motion downward.
Signedness in computing
In computingComputing
Computing is usually defined as the activity of using and improving computer hardware and software. It is the computer-specific part of information technology...
, a numeric value may be either signed or unsigned, depending on whether the computer is keeping track of a sign for the number. By restricting a variable
Variable (programming)
In computer programming, a variable is a symbolic name given to some known or unknown quantity or information, for the purpose of allowing the name to be used independently of the information it represents...
to non-negative values only, one more bit
Bit
A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
can be used for storing the value of a number.
Because of the way arithmetic is done within computers, the sign of a signed variable is usually not stored as a single independent bit, but is instead stored using two's complement
Two's complement
The two's complement of a binary number is defined as the value obtained by subtracting the number from a large power of two...
or some other signed number representation.
Other meanings
In addition to the sign of a real number, the word sign is also used in various related ways throughout mathematics and the sciences:- The sign of a permutation is defined to be positive if the permutation is even, and negative if the permutation is odd.
- In graph theoryGraph theoryIn mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a signed graph is a graph in which each edge has been marked with a positive or negative sign. - In mathematical analysisMathematical analysisMathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, a signed measureSigned measureIn mathematics, signed measure is a generalization of the concept of measure by allowing it to have negative values. Some authors may call it a charge, by analogy with electric charge, which is a familiar distribution that takes on positive and negative values.-Definition:There are two slightly...
is a generalization of the concept of measureMeasure (mathematics)In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
in which the measure of a set may have positive or negative values. - In a signed-digit representationSigned-digit representationSigned-digit representation of numbers indicates that digits can be prefixed with a − sign to indicate that they are negative.Signed-digit representation can be used in low-level software and hardware to accomplish fast addition of integers because it can eliminate carries...
, each digit of a number may have a positive or negative sign. - The ideas of signed area and signed volume are sometimes used when it is convenient for certain areas or volumes to count as negative. This is particularly true in the theory of determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
s. - In physicsPhysicsPhysics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, any electric chargeElectric chargeElectric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
comes with a sign, either positive or negative. By convention, a positive charge is a charge with the same sign as that of a protonProtonThe proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....
, and a negative charge is a charge with the same sign as that of an electronElectronThe electron is a subatomic particle with a negative elementary electric charge. It has no known components or substructure; in other words, it is generally thought to be an elementary particle. An electron has a mass that is approximately 1/1836 that of the proton...
.