Slide rule
Encyclopedia

Analog computer
An analog computer is a form of computer that uses the continuously-changeable aspects of physical phenomena such as electrical, mechanical, or hydraulic quantities to model the problem being solved...
. The slide rule is used primarily for multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
and division
Division (mathematics)
right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
, and also for functions such as root
Nth root
In mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
s, logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
s and trigonometry
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
, but is not normally used for addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
or subtraction
Subtraction
In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
.
Slide rules come in a diverse range of styles and generally appear in a linear or circular form with a standardized set of markings (scales) essential to performing mathematical computations. Slide rules manufactured for specialized fields such as aviation
Aviation
Aviation is the design, development, production, operation, and use of aircraft, especially heavier-than-air aircraft. Aviation is derived from avis, the Latin word for bird.-History:...
or finance
Finance
"Finance" is often defined simply as the management of money or “funds” management Modern finance, however, is a family of business activity that includes the origination, marketing, and management of cash and money surrogates through a variety of capital accounts, instruments, and markets created...
typically feature additional scales that aid in calculations common to that field.
William Oughtred
William Oughtred
William Oughtred was an English mathematician.After John Napier invented logarithms, and Edmund Gunter created the logarithmic scales upon which slide rules are based, it was Oughtred who first used two such scales sliding by one another to perform direct multiplication and division; and he is...
and others developed the slide rule in the 17th century based on the emerging work on logarithms by John Napier
John Napier
John Napier of Merchiston – also signed as Neper, Nepair – named Marvellous Merchiston, was a Scottish mathematician, physicist, astronomer & astrologer, and also the 8th Laird of Merchistoun. He was the son of Sir Archibald Napier of Merchiston. John Napier is most renowned as the discoverer...
. Before the advent of the pocket calculator
Calculator
An electronic calculator is a small, portable, usually inexpensive electronic device used to perform the basic operations of arithmetic. Modern calculators are more portable than most computers, though most PDAs are comparable in size to handheld calculators.The first solid-state electronic...
, it was the most commonly used calculation tool in science
Science
Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...
and engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
. The use of slide rules continued to grow through the 1950s and 1960s even as digital computing devices
Computer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
were being gradually introduced; but around 1974 the electronic scientific calculator
Scientific calculator
A scientific calculator is a type of electronic calculator, usually but not always handheld, designed to calculate problems in science, engineering, and mathematics...
made it largely obsolete and most suppliers left the business.

Basic concepts

Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
s, exponentials
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
, logarithms, and trigonometric function
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s.
Scales may be grouped in decades, which are numbers ranging from 1 to 10 (i.e. 10n to 10n+1). Thus single decade scales C and D range from 1 to 10 across the entire width of the slide rule while double decade scales A and B range from 1 to 100 over the width of the slide rule.
In general, mathematical calculations are performed by aligning a mark on the sliding central strip with a mark on one of the fixed strips, and then observing the relative positions of other marks on the strips. Number
Number
A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....
s aligned with the marks give the approximate value of the product
Product (mathematics)
In mathematics, a product is the result of multiplying, or an expression that identifies factors to be multiplied. The order in which real or complex numbers are multiplied has no bearing on the product; this is known as the commutative law of multiplication...
, quotient
Quotient
In mathematics, a quotient is the result of division. For example, when dividing 6 by 3, the quotient is 2, while 6 is called the dividend, and 3 the divisor. The quotient further is expressed as the number of times the divisor divides into the dividend e.g. The quotient of 6 and 2 is also 3.A...
, or other calculated result.
The user determines the location of the decimal point in the result, based on mental estimation. Scientific notation
Scientific notation
Scientific notation is a way of writing numbers that are too large or too small to be conveniently written in standard decimal notation. Scientific notation has a number of useful properties and is commonly used in calculators and by scientists, mathematicians, doctors, and engineers.In scientific...
is used to track the decimal point in more formal calculations. Addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
and subtraction
Subtraction
In arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
steps in a calculation are generally done mentally or on paper, not on the slide rule.
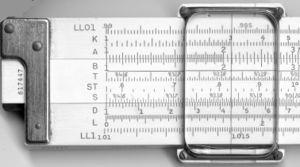
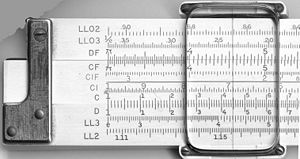
Most slide rules consist of three linear strips of the same length, aligned in parallel and interlocked so that the central strip can be moved lengthwise relative to the other two. The outer two strips are fixed so that their relative positions do not change.
Some slide rules ("duplex" models) have scales on both sides of the rule and slide strip, others on one side of the outer strips and both sides of the slide strip (which can usually be pulled out, flipped over and reinserted for convenience), still others on one side only ("simplex" rules). A sliding cursor with a vertical alignment line is used to find corresponding points on scales that are not adjacent to each other or, in duplex models, are on the other side of the rule. The cursor can also record an intermediate result on any of the scales.
Multiplication
A logarithm transforms the operations of multiplication and division to addition and subtraction according to the rules and
and 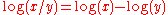 .
.Moving the top scale to the right by a distance of
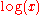 , by matching the beginning of the top scale with the label
, by matching the beginning of the top scale with the label  on the bottom, aligns each number
on the bottom, aligns each number 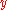 , at position
, at position 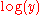 on the top scale, with the number at position
on the top scale, with the number at position  on the bottom scale. Because
on the bottom scale. Because 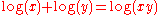 , this position on the bottom scale gives
, this position on the bottom scale gives  , the product of
, the product of  and
and 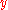 . For example, to calculate 3×2, the 1 on the top scale is moved to the 2 on the bottom scale. The answer, 6, is read off the bottom scale where 3 is on the top scale. In general, the 1 on the top is moved to a factor on the bottom, and the answer is read off the bottom where the other factor is on the top. This works because the distances from the "1" are proportional to the logarithms of the marked values:
. For example, to calculate 3×2, the 1 on the top scale is moved to the 2 on the bottom scale. The answer, 6, is read off the bottom scale where 3 is on the top scale. In general, the 1 on the top is moved to a factor on the bottom, and the answer is read off the bottom where the other factor is on the top. This works because the distances from the "1" are proportional to the logarithms of the marked values:Operations may go "off the scale;" for example, the diagram above shows that the slide rule has not positioned the 7 on the upper scale above any number on the lower scale, so it does not give any answer for 2×7. In such cases, the user may slide the upper scale to the left until its right index aligns with the 2, effectively dividing by 10 (by subtracting the full length of the C-scale) and then multiplying by 7, as in the illustration below:

Here the user of the slide rule must remember to adjust the decimal point appropriately to correct the final answer. We wanted to find 2×7, but instead we calculated (2/10)×7=0.2x7=1.4. So the true answer is not 1.4 but 14. Resetting the slide is not the only way to handle multiplications that would result in off-scale results, such as 2×7; some other methods are:
- Use the double-decade scales A and B.
- Use the folded scales. In this example, set the left 1 of C opposite the 2 of D. Move the cursor to 7 on CF, and read the result from DF.
- Use the CI inverted scale. Position the 7 on the CI scale above the 2 on the D scale, and then read the result off of the D scale, below the 1 on the CI scale. Since 1 occurs in two places on the CI scale, one of them will always be on-scale.
- Use both the CI inverted scale and the C scale. Line up the 2 of CI with the 1 of D, and read the result from D, below the 7 on the C scale.
Method 1 is easy to understand, but entails a loss of precision. Method 3 has the advantage that it only involves two scales.
Division
The illustration below demonstrates the computation of 5.5/2. The 2 on the top scale is placed over the 5.5 on the bottom scale. The 1 on the top scale lies above the quotient, 2.75. There is more than one method for doing division, but the method presented here has the advantage that the final result cannot be off-scale, because one has a choice of using the 1 at either end.
Other operations
In addition to the logarithmic scales, some slide rules have other mathematical functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s encoded on other auxiliary scales. The most popular were trigonometric
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
, usually sine
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
and tangent, common logarithm
Common logarithm
The common logarithm is the logarithm with base 10. It is also known as the decadic logarithm, named after its base. It is indicated by log10, or sometimes Log with a capital L...
(log10) (for taking the log of a value on a multiplier scale), natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
(ln) and exponential
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
(ex) scales. Some rules include a Pythagorean
Pythagoras
Pythagoras of Samos was an Ionian Greek philosopher, mathematician, and founder of the religious movement called Pythagoreanism. Most of the information about Pythagoras was written down centuries after he lived, so very little reliable information is known about him...
scale, to figure sides of triangles, and a scale to figure circles. Others feature scales for calculating hyperbolic functions. On linear rules, the scales and their labeling are highly standardized, with variation usually occurring only in terms of which scales are included and in what order:
| A, B | two-decade logarithmic scales, used for finding square roots and squares of numbers |
| C, D | single-decade logarithmic scales |
| K | three-decade logarithmic scale, used for finding cube roots and cubes of numbers |
| CF, DF | "folded" versions of the C and D scales that start from π Pi ' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants... rather than from unity; these are convenient in two cases. First when the user guesses a product will be close to 10 but is not sure whether it will be slightly less or slightly more than 10, the folded scales avoid the possibility of going off the scale. Second, by making the start π rather than the square root of 10, multiplying or dividing by π (as is common in science and engineering formulas) is simplified. |
| CI, DI, DIF | "inverted" scales, running from right to left, used to simplify 1/x steps |
| S | used for finding sines and cosines on the D scale |
| T, T1, T2 | used for finding tangents and cotangents on the D and DI scales |
| ST, SRT | used for sines and tangents of small angles and degree–radian conversion |
| L | a linear scale, used along with the C and D scales for finding base-10 logarithms and powers of 10 |
| LLn | a set of log-log scales, used for finding logarithms and exponentials of numbers |
| Ln | a linear scale, used along with the C and D scales for finding natural (base e) logarithms and  |
EWLINE
|
||
| The scales on the front and back of a Keuffel and Esser Keuffel and Esser The Keuffel and Esser Co. was a drafting instrument and supplies company founded in 1867 by German immigrants William J. D. Keuffel and Herman Esser.- Overview :... (K&E) 4081-3 slide rule. |
The Binary Slide Rule manufactured by Gilson in 1931 performed an addition and subtraction function limited to fraction
Fraction (mathematics)
A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, we specify how many parts of a certain size there are, for example, one-half, five-eighths and three-quarters.A common or "vulgar" fraction, such as 1/2, 5/8, 3/4, etc., consists...
s.
Roots and powers
There are single-decade (C and D), double-decade (A and B), and triple-decade (K) scales. To compute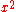 , for example, locate x on the D scale and read its square on the A scale. Inverting this process allows square roots to be found, and similarly for the powers 3, 1/3, 2/3, and 3/2. Care must be taken when the base, x, is found in more than one place on its scale. For instance, there are two nines on the A scale; to find the square root of nine, use the first one; the second one gives the square root of 90.
, for example, locate x on the D scale and read its square on the A scale. Inverting this process allows square roots to be found, and similarly for the powers 3, 1/3, 2/3, and 3/2. Care must be taken when the base, x, is found in more than one place on its scale. For instance, there are two nines on the A scale; to find the square root of nine, use the first one; the second one gives the square root of 90.For
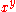 problems, use the LL scales. When several LL scales are present, use the one with x on it. First, align the leftmost 1 on the C scale with x on the LL scale. Then, find y on the C scale and go down to the LL scale with x on it. That scale will indicate the answer. If y is "off the scale," locate
problems, use the LL scales. When several LL scales are present, use the one with x on it. First, align the leftmost 1 on the C scale with x on the LL scale. Then, find y on the C scale and go down to the LL scale with x on it. That scale will indicate the answer. If y is "off the scale," locate 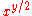 and square it using the A and B scales as described above.
and square it using the A and B scales as described above.Trigonometry
The S, T, and ST scales are used for trig functions and multiples of trig functions, for angles in degrees.For angles from around 5.7 up to 90 degrees, sines are found by comparing the S scale with C; though on many closed-body rules the S scale relates to the A scale instead, and what follows must be adjusted appropriately. The S scale has a second set of angles (sometimes in a different color), which run in the opposite direction, and are used for cosines. Tangents are found by comparing the T scale with C for angles less than 45 degrees. for angles greater than 45 degrees the CI scale is used. Common forms such as
 can be read directly from x on the S scale to the result on the D scale, when the C-scale index is set at k. For angles below 5.7 degrees, sines, tangents, and radians are approximately equal, and are found on the ST or SRT (sines, radians, and tangents) scale, or simply divided by 57.3 degrees/radian
can be read directly from x on the S scale to the result on the D scale, when the C-scale index is set at k. For angles below 5.7 degrees, sines, tangents, and radians are approximately equal, and are found on the ST or SRT (sines, radians, and tangents) scale, or simply divided by 57.3 degrees/radianRadian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
. Inverse trigonometric functions are found by reversing the process.
Many slide rules have S, T, and ST scales marked with degrees and minutes (e.g. some Keuffel and Esser models, late-model Teledyne-Post Mannheim-type rules). So-called decitrig models use decimal fractions of degrees instead.
Logarithms and exponentials
Base-10 logarithms and exponentials are found using the L scale, which is linear. Some slide rules have a Ln scale, which is for base e.The Ln scale was invented by an 11th grade student, Stephen B. Cohen, in 1958. The original intent was to allow the user to select an exponent x (in the range 0 to 2.3) on the Ln scale and read ex on the C (or D) scale and e–x on the CI (or DI) scale. Pickett, Inc. was given exclusive rights to the scale. Later, the inventor created a set of "marks" on the Ln scale to extend the range beyond the 2.3 limit, but Pickett never incorporated these marks on any of its slide rules.
Addition and subtraction
Slide rules are not typically used for addition and subtraction, but it is nevertheless possible to do so using two different techniques.The first method to perform addition and subtraction on the C and D (or any comparable scales) requires converting the problem into one of division. For addition, the quotient of the two variables plus one times the divisor equals their sum:
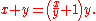
For subtraction, the quotient of the two variables minus one times the divisor equals their difference:
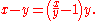
This method is similar to the addition/subtraction technique used for high-speed electronic circuits with the logarithmic number system
Logarithmic Number System
A logarithmic number system is an arithmetic system used for representing real numbers in computer and digital hardware, especially for digital signal processing.-Theory:...
in specialized computer applications like the Gravity Pipe
Gravity Pipe
Gravity Pipe, otherwise known as GRAPE, is a project which uses hardware acceleration to perform gravitational computations. Integrated with Beowulf-style commodity computers, the GRAPE system calculates the force of gravity that a given mass, such as a star, exerts on others...
(GRAPE) supercomputer and hidden Markov models.
The second method utilizes a sliding linear L scale available on some models. Addition and subtraction are performed by sliding the cursor left (for subtraction) or right (for addition) then returning the slide to 0 to read the result.
Standard linear rules
The width of the slide rule is quoted in terms of the nominal width of the scales. Scales on the most common "10-inch" models are actually 25 cm, as they were made to metric standards, though some rules offer slightly extended scales to simplify manipulation when a result overflowed. Pocket rules are typically 5 inches. Models a couple of metres wide were sold to be hung in classrooms for teaching purposes.Typically the divisions mark a scale to a precision of two significant figures
Significant figures
The significant figures of a number are those digits that carry meaning contributing to its precision. This includes all digits except:...
, and the user estimates the third figure. Some high-end slide rules have magnifier cursors that make the markings easier to see. Such cursors can effectively double the accuracy of readings, permitting a 10-inch slide rule to serve as well as a 20-inch.
Various other conveniences have been developed. Trigonometric scales are sometimes dual-labeled, in black and red, with complementary angles, the so-called "Darmstadt" style. Duplex slide rules often duplicate some of the scales on the back. Scales are often "split" to get higher accuracy.
Circular slide rules


The basic advantage of a circular slide rule is that the widest dimension of the tool was reduced by a factor of about 3 (i.e. by π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
). For example, a 10 cm circular would have a maximum precision approximately equal to a 31.4 cm ordinary slide rule. Circular slide rules also eliminate "off-scale" calculations, because the scales were designed to "wrap around"; they never have to be reoriented when results are near 1.0—the rule is always on scale. However, for non-cyclical non-spiral scales such as S, T, and LL's, the scale width is narrowed to make room for end margins.
Circular slide rules are mechanically more rugged and smoother-moving, but their scale alignment precision is sensitive to the centering of a central pivot; a minute 0.1 mm off-centre of the pivot can result in a 0.2mm worst case alignment error. The pivot, however, does prevent scratching of the face and cursors. The highest accuracy scales are placed on the outer rings. Rather than "split" scales, high-end circular rules use spiral scales for more complex operations like log-of-log scales. One eight-inch premium circular rule had a 50-inch spiral log-log scale.
The main disadvantages of circular slide rules are the difficulty in locating figures along a dish, and limited number of scales. Another drawback of circular slide rules is that less-important scales are closer to the center, and have lower precisions. Most students learned slide rule use on the linear slide rules, and did not find reason to switch.
One slide rule remaining in daily use around the world is the E6B
E6B
The E6B Flight Computer, or simply the "whiz wheel", is a form of circular slide rule used in aviation. They are mostly used in flight training, but many professional and even airline pilots still carry and use these flight computers...
. This is a circular slide rule first created in the 1930s for aircraft
Aircraft
An aircraft is a vehicle that is able to fly by gaining support from the air, or, in general, the atmosphere of a planet. An aircraft counters the force of gravity by using either static lift or by using the dynamic lift of an airfoil, or in a few cases the downward thrust from jet engines.Although...
pilot
Aviator
An aviator is a person who flies an aircraft. The first recorded use of the term was in 1887, as a variation of 'aviation', from the Latin avis , coined in 1863 by G. de la Landelle in Aviation Ou Navigation Aérienne...
s to help with dead reckoning
Dead reckoning
In navigation, dead reckoning is the process of calculating one's current position by using a previously determined position, or fix, and advancing that position based upon known or estimated speeds over elapsed time, and course...
. With the aid of scales printed on the frame it also helps with such miscellaneous tasks as converting time, distance, speed, and temperature values, compass
Compass
A compass is a navigational instrument that shows directions in a frame of reference that is stationary relative to the surface of the earth. The frame of reference defines the four cardinal directions – north, south, east, and west. Intermediate directions are also defined...
errors, and calculating fuel use. The so-called "prayer wheel" is still available in flight shops, and remains widely used. While GPS
Global Positioning System
The Global Positioning System is a space-based global navigation satellite system that provides location and time information in all weather, anywhere on or near the Earth, where there is an unobstructed line of sight to four or more GPS satellites...
has reduced the use of dead reckoning
Dead reckoning
In navigation, dead reckoning is the process of calculating one's current position by using a previously determined position, or fix, and advancing that position based upon known or estimated speeds over elapsed time, and course...
for aerial navigation
Air navigation
The basic principles of air navigation are identical to general navigation, which includes the process of planning, recording, and controlling the movement of a craft from one place to another....
, and handheld calculators have taken over many of its functions, the E6B
E6B
The E6B Flight Computer, or simply the "whiz wheel", is a form of circular slide rule used in aviation. They are mostly used in flight training, but many professional and even airline pilots still carry and use these flight computers...
remains widely used as a primary or backup device and the majority of flight schools demand that their students have some degree of proficiency in its use.
Proportion wheels are simple circular slide rules used in graphic design to broaden or slim images and photographs. Lining up the desired values on the emmer and inner wheels (which correspond to the original and desired sizes) will display the proportion as a percentage in a small window. They are not as common since the advent of computerized layout, but are still made and used.
In 1952, Swiss
Switzerland
Switzerland name of one of the Swiss cantons. ; ; ; or ), in its full name the Swiss Confederation , is a federal republic consisting of 26 cantons, with Bern as the seat of the federal authorities. The country is situated in Western Europe,Or Central Europe depending on the definition....
watch company Breitling
Breitling
Breitling is a luxury brand of Swiss watches produced by Breitling SA, a private company headquartered in Grenchen, Canton of Solothurn . The company exclusively offered Certified Chronometers in all models since 2000...
introduced a pilot's wristwatch with an integrated circular slide rule specialized for flight calculations: the Breitling Navitimer. The Navitimer circular rule, referred to by Breitling as a "navigation computer", featured airspeed
Airspeed
Airspeed is the speed of an aircraft relative to the air. Among the common conventions for qualifying airspeed are: indicated airspeed , calibrated airspeed , true airspeed , equivalent airspeed and density airspeed....
, rate
Rate of climb
In aeronautics, the rate of climb is an aircraft's vertical speed - the rate of change in altitude. In most ICAO member countries , this is usually expressed in feet per minute and can be abbreviated as ft/min. Elsewhere, it is commonly expressed in metres per second, abbreviated as m/s...
/time of climb/descent, flight time, distance, and fuel consumption functions, as well as kilometer—nautical mile
Nautical mile
The nautical mile is a unit of length that is about one minute of arc of latitude along any meridian, but is approximately one minute of arc of longitude only at the equator...
and gallon
Gallon
The gallon is a measure of volume. Historically it has had many different definitions, but there are three definitions in current use: the imperial gallon which is used in the United Kingdom and semi-officially within Canada, the United States liquid gallon and the lesser used United States dry...
—liter
Litre
pic|200px|right|thumb|One litre is equivalent to this cubeEach side is 10 cm1 litre water = 1 kilogram water The litre is a metric system unit of volume equal to 1 cubic decimetre , to 1,000 cubic centimetres , and to 1/1,000 cubic metre...
fuel amount conversion functions.
Cylindrical slide rules

Otis King
Otis Carter Formby King was a grocer and engineer in London who invented and produced a cylindrical slide rule with helical scales, primarily for business uses initially. The product was named Otis King's Patent Calculator, and was manufactured and sold by Carbic Ltd...
and the Bygrave slide rule
Bygrave slide rule
The Bygrave slide rule is a slide rule named for its inventor, Captain L. G. Bygrave of the RAF. It was used in celestial navigation, primarily in aviation. Officially, it was called the A. M. L. Position Line Slide Rule The Bygrave slide rule is a slide rule named for its inventor, Captain L. G....
, and those with bars, such as the Thacher and some Loga models. In either case, the advantage is a much longer scale, and hence potentially higher accuracy, than a straight or circular rule.
Materials
Traditionally slide rules were made out of hard wood such as mahoganyMahogany
The name mahogany is used when referring to numerous varieties of dark-colored hardwood. It is a native American word originally used for the wood of the species Swietenia mahagoni, known as West Indian or Cuban mahogany....
or boxwood with cursors of glass and metal. At least one high precision instrument was made of steel
Steel
Steel is an alloy that consists mostly of iron and has a carbon content between 0.2% and 2.1% by weight, depending on the grade. Carbon is the most common alloying material for iron, but various other alloying elements are used, such as manganese, chromium, vanadium, and tungsten...
.
In 1895, a Japanese firm, Hemmi, started to make slide rules from bamboo
Bamboo
Bamboo is a group of perennial evergreens in the true grass family Poaceae, subfamily Bambusoideae, tribe Bambuseae. Giant bamboos are the largest members of the grass family....
, which had the advantages of being dimensionally stable, strong and naturally self-lubricating. These bamboo slide rules were introduced in Sweden in September, 1933, and probably only a little earlier in Germany. Scales were made of celluloid
Celluloid
Celluloid is the name of a class of compounds created from nitrocellulose and camphor, plus dyes and other agents. Generally regarded to be the first thermoplastic, it was first created as Parkesine in 1862 and as Xylonite in 1869, before being registered as Celluloid in 1870. Celluloid is...
or plastic. Later slide rules were made of plastic, or aluminium
Aluminium
Aluminium or aluminum is a silvery white member of the boron group of chemical elements. It has the symbol Al, and its atomic number is 13. It is not soluble in water under normal circumstances....
painted with plastic. Later cursors were acrylics
Acryl group
In organic chemistry, the acryloyl group is the functional group with structure H2C=CH–C–; it is the acyl group derived from acrylic acid. The preferred IUPAC name for the group is prop-2-enoyl, and it is also known as acrylyl or simply acryl...
or polycarbonate
Polycarbonate
PolycarbonatePhysical PropertiesDensity 1.20–1.22 g/cm3Abbe number 34.0Refractive index 1.584–1.586FlammabilityV0-V2Limiting oxygen index25–27%Water absorption – Equilibrium0.16–0.35%Water absorption – over 24 hours0.1%...
s sliding on Teflon
Polytetrafluoroethylene
Polytetrafluoroethylene is a synthetic fluoropolymer of tetrafluoroethylene that finds numerous applications. PTFE is most well known by the DuPont brand name Teflon....
bearings.
All premium slide rules had numbers and scales engraved, and then filled with paint or other resin
Resin
Resin in the most specific use of the term is a hydrocarbon secretion of many plants, particularly coniferous trees. Resins are valued for their chemical properties and associated uses, such as the production of varnishes, adhesives, and food glazing agents; as an important source of raw materials...
. Painted or imprinted slide rules were viewed as inferior because the markings could wear off. Nevertheless, Pickett, probably America's most successful slide rule company, made all printed scales. Premium slide rules included clever catches so the rule would not fall apart by accident, and bumpers to protect the scales and cursor from rubbing on tabletops. The recommended cleaning method for engraved markings is to scrub lightly with steel-wool. For painted slide rules, and the faint of heart, use diluted commercial window-cleaning fluid and a soft cloth.
History

John Napier
John Napier of Merchiston – also signed as Neper, Nepair – named Marvellous Merchiston, was a Scottish mathematician, physicist, astronomer & astrologer, and also the 8th Laird of Merchistoun. He was the son of Sir Archibald Napier of Merchiston. John Napier is most renowned as the discoverer...
's publication of the concept of the logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
. Edmund Gunter
Edmund Gunter
Edmund Gunter , English mathematician, of Welsh descent, was born in Hertfordshire in 1581.He was educated at Westminster School, and in 1599 was elected a student of Christ Church, Oxford. He took orders, became a preacher in 1614, and in 1615 proceeded to the degree of bachelor in divinity...
of Oxford developed a calculating device with a single logarithmic scale, which, with additional measuring tools, could be used to multiply and divide. The first description of this scale was published in Paris in 1624 by Edmund Wingate
Edmund Wingate
Edmund Wingate was an English mathematical and legal writer, one of the first to publish in the 1620s on the principle of the slide rule, and later the author of some popular expository works...
(c.1593–1656), an English mathematician, in a book entitled L'usage de la reigle de proportion en l'arithmetique & geometrie. The book contains a double scale on one side of which is a logarithmic scale and on the other a tabular scale. In 1630, William Oughtred
William Oughtred
William Oughtred was an English mathematician.After John Napier invented logarithms, and Edmund Gunter created the logarithmic scales upon which slide rules are based, it was Oughtred who first used two such scales sliding by one another to perform direct multiplication and division; and he is...
of Cambridge invented a circular slide rule, and in 1632 he combined two Gunter rules, held together with the hands, to make a device that is recognizably the modern slide rule. Like his contemporary at Cambridge, Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
, Oughtred taught his ideas privately to his students, but delayed in publishing them, and like Newton, he became involved in a vitriolic controversy over priority, with his one-time student Richard Delamain and the prior claims of Wingate. Oughtred's ideas were only made public in publications of his student William Forster in 1632 and 1653.
In 1677, Henry Coggeshall created a two-foot folding rule for timber measure, called the Coggeshall slide rule
Coggeshall slide rule
In measurement, the Coggeshall slide rule, also called a carpenter's slide rule, was a slide rule designed by Henry Coggeshall in 1677 to facilitate measuring the dimensions, superficies, and solidity of timber. With his original design and later improvements, Coggeshall's slide rule brought the...
. His design and uses for the tool gave the slide rule purpose outside of mathematical inquiry.
In 1722, Warner introduced the two- and three-decade scales, and in 1755 Everard included an inverted scale; a slide rule containing all of these scales is usually known as a "polyphase" rule.
In 1815, Peter Mark Roget invented the log log slide rule, which included a scale displaying the logarithm of the logarithm. This allowed the user to directly perform calculations involving roots and exponents. This was especially useful for fractional powers.
In 1821, Nathaniel Bowditch
Nathaniel Bowditch
Nathaniel Bowditch was an early American mathematician remembered for his work on ocean navigation. He is often credited as the founder of modern maritime navigation; his book The New American Practical Navigator, first published in 1802, is still carried on board every commissioned U.S...
, in the American Practical Navigator, described the use of a "sliding rule" which contained scales trigonometric functions on the fixed part and a line of log-sines and log-tans on the slider. This device was used to solve navigation problems.
Modern form
The more modern form was created in 1859 by French artillery lieutenant Amédée Mannheim, "who was fortunate in having his rule made by a firm of national reputation and in having it adopted by the French Artillery." It was around that time, as engineeringEngineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
became a recognized professional activity, that slide rules came into wide use in Europe. They did not become common in the United States until 1881, when Edwin Thacher introduced a cylindrical rule there. The duplex rule was invented by William Cox in 1891, and was produced by Keuffel and Esser Co. of New York.
Astronomical work also required fine computations, and in the 19th century Germany a steel slide rule about 2 meters long was used at one observatory. It had a microscope
Microscope
A microscope is an instrument used to see objects that are too small for the naked eye. The science of investigating small objects using such an instrument is called microscopy...
attached, giving it accuracy to six decimal places.

Stethoscope
The stethoscope is an acoustic medical device for auscultation, or listening to the internal sounds of an animal body. It is often used to listen to lung and heart sounds. It is also used to listen to intestines and blood flow in arteries and veins...
symbolizes the medical profession). German rocket scientist Wernher von Braun
Wernher von Braun
Wernher Magnus Maximilian, Freiherr von Braun was a German rocket scientist, aerospace engineer, space architect, and one of the leading figures in the development of rocket technology in Nazi Germany during World War II and in the United States after that.A former member of the Nazi party,...
brought two 1930s vintage Nestler slide rules with him when he moved to the U.S. after World War II to work on the American space program. Throughout his life he never used any other pocket calculating devices; slide rules served him perfectly well for making quick estimates of rocket design parameters and other figures. Aluminium Pickett
Pickett
Pickett is a surname of English origin, and may refer to:* Albert J. Pickett , American historian* Allistair Pickett , Australian rules footballer* Bill Pickett , American cowboy and rodeo performer...
-brand slide rules were carried on five Apollo
Project Apollo
The Apollo program was the spaceflight effort carried out by the United States' National Aeronautics and Space Administration , that landed the first humans on Earth's Moon. Conceived during the Presidency of Dwight D. Eisenhower, Apollo began in earnest after President John F...
space missions, including to the moon, according to advertising on Pickett's N600 slide rule boxes.
Some engineering students and engineers carried ten-inch slide rules in belt holsters, and even into the mid 1970s this was a common sight on campuses. Students also might keep a ten- or twenty-inch rule for precision work at home or the office while carrying a five-inch pocket slide rule around with them.
In 2004, education researchers David B. Sher and Dean C. Nataro conceived a new type of slide rule based on prosthaphaeresis
Prosthaphaeresis
Prosthaphaeresis was an algorithm used in the late 16th century and early 17th century for approximate multiplication and division using formulas from trigonometry. For the 25 years preceding the invention of the logarithm in 1614, it was the only known generally-applicable way of approximating...
, an algorithm for rapidly computing products that predates logarithms. There has been little practical interest in constructing one beyond the initial prototype, however.
Specialized calculators


Photography
Photography is the art, science and practice of creating durable images by recording light or other electromagnetic radiation, either electronically by means of an image sensor or chemically by means of a light-sensitive material such as photographic film...
applications; for example, the actinograph
Actinograph
An actinograph is an instrument for measuring or estimating the amount of light available, in terms of its ability to expose photographic film...
of Hurter and Driffield
Hurter and Driffield
Ferdinand Hurter and Vero Charles Driffield were nineteenth-century photographic scientists who brought quantitative scientific practice to photography through the methods of sensitometry and densitometry....
was a two-slide boxwood, brass, and cardboard device for estimating exposure from time of day, time of year, and latitude.
Specialized slide rules were invented for various forms of engineering, business and banking. These often had common calculations directly expressed as special scales, for example loan calculations, optimal purchase quantities, or particular engineering equations. For example, the Fisher Controls company distributed a customized slide rule adapted to solving the equations used for selecting the proper size of industrial flow control valve
Valve
A valve is a device that regulates, directs or controls the flow of a fluid by opening, closing, or partially obstructing various passageways. Valves are technically pipe fittings, but are usually discussed as a separate category...
s.
In World War II
World War II
World War II, or the Second World War , was a global conflict lasting from 1939 to 1945, involving most of the world's nations—including all of the great powers—eventually forming two opposing military alliances: the Allies and the Axis...
, bombardiers and navigators who required quick calculations often used specialized slide rules. One office of the U.S. Navy actually designed a generic slide rule "chassis" with an aluminium body and plastic cursor into which celluloid cards (printed on both sides) could be placed for special calculations. The process was invented to calculate range, fuel use and altitude for aircraft
Aircraft
An aircraft is a vehicle that is able to fly by gaining support from the air, or, in general, the atmosphere of a planet. An aircraft counters the force of gravity by using either static lift or by using the dynamic lift of an airfoil, or in a few cases the downward thrust from jet engines.Although...
, and then adapted to many other purposes.
Decline

Fortran
Fortran is a general-purpose, procedural, imperative programming language that is especially suited to numeric computation and scientific computing...
in 1957 made computers practical for solving modest size mathematical problems. IBM
IBM
International Business Machines Corporation or IBM is an American multinational technology and consulting corporation headquartered in Armonk, New York, United States. IBM manufactures and sells computer hardware and software, and it offers infrastructure, hosting and consulting services in areas...
introduced a series of more affordable computers, the IBM 650
IBM 650
The IBM 650 was one of IBM’s early computers, and the world’s first mass-produced computer. It was announced in 1953, and over 2000 systems were produced between the first shipment in 1954 and its final manufacture in 1962...
(1954), IBM 1620
IBM 1620
The IBM 1620 was announced by IBM on October 21, 1959, and marketed as an inexpensive "scientific computer". After a total production of about two thousand machines, it was withdrawn on November 19, 1970...
(1959), IBM 1130
IBM 1130
The IBM 1130 Computing System was introduced in 1965. It was IBM's least-expensive computer to date, and was aimed at price-sensitive, computing-intensive technical markets like education and engineering. It succeeded the IBM 1620 in that market segment. The IBM 1800 was a process control variant...
(1965) addressed to the science and engineering market. The BASIC programming language (1964) made it easy for students to use computers. The DEC PDP-8
PDP-8
The 12-bit PDP-8 was the first successful commercial minicomputer, produced by Digital Equipment Corporation in the 1960s. DEC introduced it on 22 March 1965, and sold more than 50,000 systems, the most of any computer up to that date. It was the first widely sold computer in the DEC PDP series of...
minicomputer was introduced in 1965.
Computers also changed the nature of calculation. With slide rules, there was a great emphasis on working the algebra to get expressions into the most computable form. Users of slide rules would simply approximate or drop small terms to simplify the calculation. Fortran allowed complicated formulas to be typed in from textbook
Textbook
A textbook or coursebook is a manual of instruction in any branch of study. Textbooks are produced according to the demands of educational institutions...
s without the effort of reformulation. Numerical integration
Numerical integration
In numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...
was often easier than trying to find closed-form
Closed-form expression
In mathematics, an expression is said to be a closed-form expression if it can be expressed analytically in terms of a bounded number of certain "well-known" functions...
solutions for difficult problems. The young engineer asking for computer time to solve a problem that could have been done by a few swipes on the slide rule became a humorous cliché.
The availability of mainframe computing did not however significantly affect the ubiquitous use of the slide rule until cheap hand held electronic calculator
Calculator
An electronic calculator is a small, portable, usually inexpensive electronic device used to perform the basic operations of arithmetic. Modern calculators are more portable than most computers, though most PDAs are comparable in size to handheld calculators.The first solid-state electronic...
s for scientific and engineering purposes became available in the mid 1970s at which point they rapidly fell out of use. The first included the Wang Laboratories
Wang Laboratories
Wang Laboratories was a computer company founded in 1951 by Dr. An Wang and Dr. G. Y. Chu. The company was successively headquartered in Cambridge , Tewksbury , and finally in Lowell, Massachusetts . At its peak in the 1980s, Wang Laboratories had annual revenues of $3 billion and employed over...
LOCI-2, introduced in 1965, which used logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
s for multiplication and division and the Hewlett-Packard
Hewlett-Packard
Hewlett-Packard Company or HP is an American multinational information technology corporation headquartered in Palo Alto, California, USA that provides products, technologies, softwares, solutions and services to consumers, small- and medium-sized businesses and large enterprises, including...
HP-9100, introduced in 1968. The HP-9100 had trigonometric function
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s (sin, cos, tan) in addition to exponentials and logarithms. It used the CORDIC
CORDIC
CORDIC is a simple and efficient algorithm to calculate hyperbolic and trigonometric functions...
(coordinate rotation digital computer) algorithm, which allows for calculation of trigonometric functions using only shift and add operations. This method facilitated the development of ever smaller scientific calculators.
The era of the slide rule ended with the launch of pocket-sized scientific calculators, of which the 1972 Hewlett-Packard HP-35
HP-35
The HP-35 was Hewlett-Packard's first pocket calculator and the world's first scientific pocket calculator . Like some of HP's desktop calculators it used reverse Polish notation. Introduced at US$395, the HP-35 was available from 1972 to 1975.Market studies at the time had shown no market for...
was the first. Introduced at US$
United States dollar
The United States dollar , also referred to as the American dollar, is the official currency of the United States of America. It is divided into 100 smaller units called cents or pennies....
395, even this was considered expensive for most students, but by 1975 basic four-function electronic calculators could be purchased for less than $50. By 1976 the TI-30
TI-30
The TI-30 was a scientific calculator manufactured by Texas Instruments, the first model of which was introduced in 1976. While the original TI-30 left production in 1983 after several design revisions, TI maintains the TI-30 designation as a branding for its low and mid-range scientific...
offered a scientific calculator for less than $25. After this time, the market for slide rules dwindled quickly as small scientific calculators became affordable.
Compared to electronic digital calculators
Compared to the portable electronic digital calculators that were introduced in the early 1970s, slide rules had various advantages and disadvantages.Advantages
- The spatial, manual operation of slide rules cultivates in the user an intuition for numerical relationships and scale that people who have used only digital calculators often lack. Since users must explicitly note the order of magnitudeOrder of magnitudeAn order of magnitude is the class of scale or magnitude of any amount, where each class contains values of a fixed ratio to the class preceding it. In its most common usage, the amount being scaled is 10 and the scale is the exponent being applied to this amount...
at each step in order to interpret the results, they are less likely to make extreme calculation errors; users are forced to use common sense and an understanding of the subject as they calculate. Since order of magnitude gets the greatest prominence when using a slide rule, and precision is limited only to the few digits that are normally useful, users are less likely to make errors of false precisionFalse precisionFalse precision occurs when numerical data are presented in a manner that implies better precision than is actually the case; since precision is a limit to accuracy, this often leads to overconfidence in the accuracy as well.In science and engineering, convention dictates that...
. - When performing a sequence of multiplications or divisions by the same number, the answer can often be determined by merely glancing at the slide rule without any manipulation. This can be especially useful when calculating percentages (e.g. for test scores) or when comparing prices (e.g. in dollars per kilogram). Multiple speed-time-distance calculations can be performed hands-free at a glance with a slide rule.
- Other useful constants such as pounds to kilograms can be easily marked on the rule and used directly in calculations.
- A slide rule does not depend on electricityElectricityElectricity is a general term encompassing a variety of phenomena resulting from the presence and flow of electric charge. These include many easily recognizable phenomena, such as lightning, static electricity, and the flow of electrical current in an electrical wire...
or batteries. - The principle of operation of a slide rule can be demonstrated with a pair of hand-made paper scales.
- A slide rule displays all the terms of a calculation along with the result. This eliminates uncertainty about what calculation was actually performed.
- A slide rule is physically more durable than an electronic calculator and is impervious to moisture and immersion in water.
For many of these reasons slide rules are still commonly used in aviation, particularly for smaller planes. They are only being replaced by integrated, special purpose and expensive flight computers, and not general-purpose calculators. Many sailors keep them as backup systems for navigation against electric failures or running out of batteries on long blue-water legs.
Disadvantages
- Most people find slide rules difficult to learn and use. Even during their heyday, they never caught on with the general public.
- Doing a calculation on a slide rule tends to be slower than on a calculator. This led engineers to take mathematical shortcuts favoring operations that were easy on a slide rule, creating inaccuracies and mistakes.
- A slide rule requires the user to mentally calculate the order of magnitudeOrder of magnitudeAn order of magnitude is the class of scale or magnitude of any amount, where each class contains values of a fixed ratio to the class preceding it. In its most common usage, the amount being scaled is 10 and the scale is the exponent being applied to this amount...
of the results. For example, 1.5 × 30 (which equals 45) will show the same result as 1,500,000 × 0.03 (which equals 45,000). This forces the user to keep track of magnitude in short-term memoryShort-term memoryShort-term memory is the capacity for holding a small amount of information in mind in an active, readily available state for a short period of time. The duration of short-term memory is believed to be in the order of seconds. A commonly cited capacity is 7 ± 2 elements...
(which is error-prone), keep notes (which is cumbersome) or reason about it in every step (which distracts from the other calculation requirements). - Addition and subtraction are not well-supported operations on slide rules.
- The typical precision of a slide rule is about three significant digits, compared to many digits on digital calculators (however, just 2 significant digits is adequate for many engineering calculations).
- Errors may arise from mechanical imprecision in slide rules that are warped by heat or use or that were poorly constructed.
Finding and collecting slide rules
There are still people who prefer a slide rule over an electronic calculator as a practical computing device. Many others keep their old slide rules out of a sense of nostalgia, or collect slide rules as a hobby.A popular collectible model is the Keuffel & Esser Deci-Lon, a premium scientific and engineering slide rule available both in a ten-inch "regular" (Deci-Lon 10) and a five-inch "pocket" (Deci-Lon 5) variant. Another prized American model is the eight-inch Scientific Instruments circular rule. Of European rules, Faber-Castell
Faber-Castell
Faber-Castell is one of the world's largest manufacturers of pens, pencils, other office supplies and art supplies, as well as high-end writing instruments and luxury leather goods...
's high-end models are the most popular among collectors.
Although there is a large supply of slide rules circulating on the market, specimens in good condition tend to be expensive. Many rules found for sale on online auction sites are damaged or have missing parts, and the seller may not know enough to supply the relevant information. Replacement parts are scarce, and therefore expensive, and are generally only available for separate purchase on individual collectors' web sites. The Keuffel and Esser rules from the period up to about 1950 are particularly problematic, because the end-pieces on the cursors, made of celluloid
Celluloid
Celluloid is the name of a class of compounds created from nitrocellulose and camphor, plus dyes and other agents. Generally regarded to be the first thermoplastic, it was first created as Parkesine in 1862 and as Xylonite in 1869, before being registered as Celluloid in 1870. Celluloid is...
, tend to break down chemically over time.
There are still a handful of sources for brand new slide rules. The Concise Company of Tokyo, which began as a manufacturer of circular slide rules in July 1954, continues to make and sell them today. And in September 2009, on-line retailer ThinkGeek
ThinkGeek
ThinkGeek is an American online retailer that caters to computer enthusiasts and other "geeky" social groups. Their merchandise includes clothing, electronic and scientific gadgets, unusual computer peripherals, office toys, pet toys, child toys, and caffeinated drinks and candy...
introduced its own brand of straight slide rules, which they describe as "faithful replica[s]" that are "individually hand tooled" due to a stated lack of any existing manufacturers. The E6B
E6B
The E6B Flight Computer, or simply the "whiz wheel", is a form of circular slide rule used in aviation. They are mostly used in flight training, but many professional and even airline pilots still carry and use these flight computers...
circular slide rule used by pilots has been in continuous production and remains available in a variety of models. Proportion wheels are still used in graphic design.
External links
General information, history:- International Slide Rule Museum
- History and collection of slide rules Giovanni Pastore — Italy — English version
- The history, theory and use of the engineering slide rule — By Dr James B. Calvert, University of Denver
- Oughtred Society Slide Rule Home Page — Dedicated to the preservation and history of slide rules
- Derek's virtual slide rule gallery — Javascript simulations of historical slide rules
- Reglas de Cálculo — A very big Faber Castell collection
- Collection of slide rules — French Slide Rules (Graphoplex, Tavernier-Gravet and others)