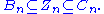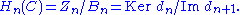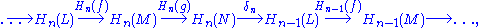Homological algebra
Encyclopedia
Homological algebra is the branch of mathematics
which studies homology
in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology
(a precursor to algebraic topology
) and abstract algebra
(theory of modules
and syzygies
) at the end of the 19th century, chiefly by Henri Poincaré
and David Hilbert
.
The development of homological algebra was closely intertwined with the emergence of category theory
. By and large, homological algebra is the study of homological functor
s and the intricate algebraic structures that they entail. One quite useful and ubiquitous concept in mathematics is that of chain complex
es, which can be studied both through their homology and cohomology
. Homological algebra affords the means to extract information contained in these complexes and present it in the form of homological invariants
of rings
, modules, topological space
s, and other 'tangible' mathematical objects. A powerful tool for doing this is provided by spectral sequence
s.
From its very origins, homological algebra has played an enormous role in algebraic topology. Its sphere of influence has gradually expanded and presently includes commutative algebra
, algebraic geometry
, algebraic number theory
, representation theory
, mathematical physics
, operator algebra
s, complex analysis
, and the theory of partial differential equation
s. K-theory
is an independent discipline which draws upon methods of homological algebra, as does the noncommutative geometry
of Alain Connes
.
is the central notion of homological algebra. It is a sequence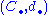 of abelian group
of abelian group
s and group homomorphism
s,
with the property that the composition of any two consecutive maps is zero:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
which studies homology
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology
Combinatorial topology
In mathematics, combinatorial topology was an older name for algebraic topology, dating from the time when topological invariants of spaces were regarded as derived from combinatorial decompositions such as simplicial complexes...
(a precursor to algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
) and abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
(theory of modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
and syzygies
Syzygy (mathematics)
In mathematics, a syzygy is a relation between the generators of a module M. The set of all such relations is called the "first syzygy module of M". A relation between generators of the first syzygy module is called a "second syzygy" of M, and the set of all such relations is called the...
) at the end of the 19th century, chiefly by Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
and David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
.
The development of homological algebra was closely intertwined with the emergence of category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
. By and large, homological algebra is the study of homological functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
s and the intricate algebraic structures that they entail. One quite useful and ubiquitous concept in mathematics is that of chain complex
Chain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
es, which can be studied both through their homology and cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
. Homological algebra affords the means to extract information contained in these complexes and present it in the form of homological invariants
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
of rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, modules, topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s, and other 'tangible' mathematical objects. A powerful tool for doing this is provided by spectral sequence
Spectral sequence
In homological algebra and algebraic topology, a spectral sequence is a means of computing homology groups by taking successive approximations...
s.
From its very origins, homological algebra has played an enormous role in algebraic topology. Its sphere of influence has gradually expanded and presently includes commutative algebra
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
, algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
, representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
, mathematical physics
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
, operator algebra
Operator algebra
In functional analysis, an operator algebra is an algebra of continuous linear operators on a topological vector space with the multiplication given by the composition of mappings...
s, complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, and the theory of partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s. K-theory
K-theory
In mathematics, K-theory originated as the study of a ring generated by vector bundles over a topological space or scheme. In algebraic topology, it is an extraordinary cohomology theory known as topological K-theory. In algebra and algebraic geometry, it is referred to as algebraic K-theory. It...
is an independent discipline which draws upon methods of homological algebra, as does the noncommutative geometry
Noncommutative geometry
Noncommutative geometry is a branch of mathematics concerned with geometric approach to noncommutative algebras, and with construction of spaces which are locally presented by noncommutative algebras of functions...
of Alain Connes
Alain Connes
Alain Connes is a French mathematician, currently Professor at the Collège de France, IHÉS, The Ohio State University and Vanderbilt University.-Work:...
.
Chain complexes and homology
The chain complexChain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
is the central notion of homological algebra. It is a sequence
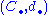 of abelian group
of abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s and group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
s,
with the property that the composition of any two consecutive maps is zero:
-
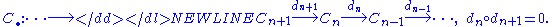
The elements of Cn are called n-chains and the homomorphisms dn are called the boundary maps or differentials. The chain groups Cn may be endowed with extra structure; for example, they may be vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s or modulesModule (mathematics)In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over a fixed ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
R. The differentials must preserve the extra structure if it exists; for example, they must be linear maps or homomorphisms of R-modules. For notational convenience, restrict attention to abelian groups (more correctly, to the categoryCategory (mathematics)In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
Ab of abelian groups); a celebrated theorem by Barry MitchellMitchell's embedding theoremMitchell's embedding theorem, also known as the Freyd–Mitchell theorem, is a result stating that every abelian category admits a full and exact embedding into the category of R-modules...
implies the results will generalize to any abelian categoryAbelian categoryIn mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
. Every chain complex defines two further sequences of abelian groups, the cycles Zn = Ker dn and the boundaries Bn = Im dn+1, where Ker d and Im d denote the kernelKernel (mathematics)In mathematics, the word kernel has several meanings. Kernel may mean a subset associated with a mapping:* The kernel of a mapping is the set of elements that map to the zero element , as in kernel of a linear operator and kernel of a matrix...
and the imageImage (mathematics)In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of d. Since the composition of two consecutive boundary maps is zero, these groups are embedded into each other as
Subgroups of abelian groups are automatically normalNormal subgroupIn abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
; therefore we can define the nth homology group Hn(C) as the factor group of the n-cycles by the n-boundaries,
A chain complex is called acyclic or an exact sequence if all its homology groups are zero.
Chain complexes arise in abundance in algebraAbstract algebraAbstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
and algebraic topologyAlgebraic topologyAlgebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
. For example, if X is a topological spaceTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
then the singular chains Cn(X) are formal linear combinationLinear combinationIn mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
s of continuous maps from the standard n-simplexSimplexIn geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
into X; if K is a simplicial complexSimplicial complexIn mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
then the simplicial chains Cn(K) are formal linear combinations of the n-simplices of X; if A = F/R is a presentation of an abelian group A by generators and relations, where F is a free abelian groupFree abelian groupIn abstract algebra, a free abelian group is an abelian group that has a "basis" in the sense that every element of the group can be written in one and only one way as a finite linear combination of elements of the basis, with integer coefficients. Hence, free abelian groups over a basis B are...
spanned by the generators and R is the subgroup of relations, then letting C1(A) = R, C0(A) = F, and Cn(A) = 0 for all other n defines a sequence of abelian groups. In all these cases, there are natural differentials dn making Cn into a chain complex, whose homology reflects the structure of the topological space X, the simplicial complex K, or the abelian group A. In the case of topological spaces, we arrive at the notion of singular homologySingular homologyIn algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
, which plays a fundamental role in investigating the properties of such spaces, for example, manifoldManifoldIn mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s.
On a philosophical level, homological algebra teaches us that certain chain complexes associated with algebraic or geometric objects (topological spaces, simplicial complexes, R-modules) contain a lot of valuable algebraic information about them, with the homology being only the most readily available part. On a technical level, homological algebra provides the tools for manipulating complexes and extracting this information. Here are two general illustrations.- Two objects X and Y are connected by a map f between them. Homological algebra studies the relation, induced by the map f, between chain complexes associated with X and Y and their homology. This is generalized to the case of several objects and maps connecting them. Phrased in the language of category theoryCategory theoryCategory theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, homological algebra studies the functorial propertiesFunctorIn category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
of various constructions of chain complexes and of the homology of these complexes. - An object X admits multiple descriptions (for example, as a topological space and as a simplicial complex) or the complex
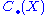 is constructed using some 'presentation' of X, which involves non-canonical choices. It is important to know the effect of change in the description of X on chain complexes associated with X. Typically, the complex and its homology
is constructed using some 'presentation' of X, which involves non-canonical choices. It is important to know the effect of change in the description of X on chain complexes associated with X. Typically, the complex and its homology 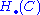 are functorial with respect to the presentation; and the homology (although not the complex itself) is actually independent of the presentation chosen, thus it is an invariantInvariant (mathematics)In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
are functorial with respect to the presentation; and the homology (although not the complex itself) is actually independent of the presentation chosen, thus it is an invariantInvariant (mathematics)In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
of X.
Functoriality
A continuous map of topological spaces gives rise to a homomorphism between their nth homology groups for all n. This basic fact of algebraic topologyAlgebraic topologyAlgebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
finds a natural explanation through certain properties of chain complexes. Since it is very common to study
several topological spaces simultaneously, in homological algebra one is led to simultaneous consideration of multiple chain complexes.
A morphism between two chain complexes, , is a family of homomorphisms of abelian groups Fn:Cn → Dn that commute with the differentials, in the sense that Fn -1 • dnC = dnD • Fn for all n. A morphism of chain complexes induces a morphism
, is a family of homomorphisms of abelian groups Fn:Cn → Dn that commute with the differentials, in the sense that Fn -1 • dnC = dnD • Fn for all n. A morphism of chain complexes induces a morphism 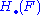 of their homology groups, consisting of the homomorphisms Hn(F): Hn(C) → Hn(D) for all n. A morphism F is called a quasi-isomorphism if it induces an isomorphism on the nth homology for all n.
of their homology groups, consisting of the homomorphisms Hn(F): Hn(C) → Hn(D) for all n. A morphism F is called a quasi-isomorphism if it induces an isomorphism on the nth homology for all n.
Many constructions of chain complexes arising in algebra and geometry, including singular homologySingular homologyIn algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
, have the following functorialityFunctorIn category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
property: if two objects X and Y are connected by a map f, then the associated chain complexes are connected by a morphism F = C(f) from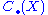 to
to 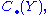 and moreover, the composition g • f of maps f: X → Y and g: Y → Z induces the morphism C(g • f) from
and moreover, the composition g • f of maps f: X → Y and g: Y → Z induces the morphism C(g • f) from 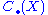 to
to  that coincides with the composition C(g) • C(f). It follows that the homology groups
that coincides with the composition C(g) • C(f). It follows that the homology groups 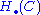 are functorial as well, so that morphisms between algebraic or topological objects give rise to compatible maps between their homology.
are functorial as well, so that morphisms between algebraic or topological objects give rise to compatible maps between their homology.
The following definition arises from a typical situation in algebra and topology. A triple consisting of three chain complexes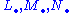 and two morphisms between them,
and two morphisms between them, 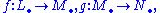
is called an exact triple, or a short exact sequence of complexes, and written as
-

if for any n, the sequence
-
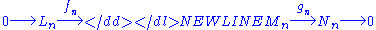
is a short exact sequence of abelian groups. By definition, this means that fn is an injection, gn is a surjection, and Im fn = Ker gn. One of the most basic theorems of homological algebra, sometimes known as the zig-zag lemmaZig-zag lemmaIn mathematics, particularly homological algebra, the zig-zag lemma asserts the existence of a particular long exact sequence in the homology groups of certain chain complexes...
, states that, in this case, there is a long exact sequence in homology
where the homology groups of L, M, and N cyclically follow each other, and δn are certain homomorphisms determined by f and g, called the connecting homomorphisms. Topological manifestations of this theorem include the Mayer–Vietoris sequence and the long exact sequence for relative homologyRelative homologyIn algebraic topology, a branch of mathematics, the homology of a topological space relative to a subspace is a construction in singular homology, for pairs of spaces. The relative homology is useful and important in several ways...
.
Foundational aspects
Cohomology theories have been defined for many different objects such as topological spaceTopological spaceTopological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s, sheavesSheaf (mathematics)In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
, groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
s, ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
s, Lie algebraLie algebraIn mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s, and C*-algebras. The study of modern algebraic geometryAlgebraic geometryAlgebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
would be almost unthinkable without sheaf cohomologySheaf cohomologyIn mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
.
Central to homological algebra is the notion of exact sequenceExact sequenceAn exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
; these can be used to perform actual calculations. A classical tool of homological algebra is that of derived functorDerived functorIn mathematics, certain functors may be derived to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics.- Motivation :...
; the most basic examples are functors Ext and Tor.
With a diverse set of applications in mind, it was natural to try to put the whole subject on a uniform basis. There were several attempts before the subject settled down. An approximate history can be stated as follows:
- CartanHenri CartanHenri Paul Cartan was a French mathematician with substantial contributions in algebraic topology. He was the son of the French mathematician Élie Cartan.-Life:...
-EilenbergSamuel EilenbergSamuel Eilenberg was a Polish and American mathematician of Jewish descent. He was born in Warsaw, Russian Empire and died in New York City, USA, where he had spent much of his career as a professor at Columbia University.He earned his Ph.D. from University of Warsaw in 1936. His thesis advisor...
: In their 1956 book "Homological Algebra", these authors used projective and injective module resolutions. - 'Tohoku': The approach in a celebrated paper by Alexander GrothendieckAlexander GrothendieckAlexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
which appeared in the Second Series of the Tohoku Mathematical JournalTohoku Mathematical JournalThe Tohoku Mathematical Journal is a mathematical research journal published by Tohoku University in Japan. It was founded in August 1911 by Tsuruichi Hayashi....
in 1957, using the abelian categoryAbelian categoryIn mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
concept (to include sheavesSheaf (mathematics)In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
of abelian groups). - The derived categoryDerived categoryIn mathematics, the derived category D of an abelian category C is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on C...
of Grothendieck and VerdierJean-Louis VerdierJean-Louis Verdier was a French mathematician who worked, under the guidance of Alexander Grothendieck, on derived categories and Verdier duality...
. Derived categories date back to Verdier's 1967 thesis. They are examples of triangulated categoriesTriangulated categoryA triangulated category is a mathematical category satisfying some axioms that are based on the properties of the homotopy category of spectra, and the derived category of an abelian category. A t-category is a triangulated category with a t-structure.- History :The notion of a derived category...
used in a number of modern theories.
These move from computability to generality.
The computational sledgehammer par excellence is the spectral sequenceSpectral sequenceIn homological algebra and algebraic topology, a spectral sequence is a means of computing homology groups by taking successive approximations...
; these are essential in the Cartan-Eilenberg and Tohoku approaches where they are needed, for instance, to compute the derived functors of a composition of two functors. Spectral sequences are less essential in the derived category approach, but still play a role whenever concrete computations are necessary.
There have been attempts at 'non-commutative' theories which extend first cohomology as torsors (important in Galois cohomologyGalois cohomologyIn mathematics, Galois cohomology is the study of the group cohomology of Galois modules, that is, the application of homological algebra to modules for Galois groups...
).
See also
- Abstract nonsenseAbstract nonsenseIn mathematics, abstract nonsense, general abstract nonsense, and general nonsense are terms used facetiously by some mathematicians to describe certain kinds of arguments and methods related to category theory. roughly speaking, category theory is the study of the general form of mathematical...
, a (sarcastic 1950´s) term for homological algebra and category theoryCategory theoryCategory theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions... - Homotopical algebraHomotopical algebraIn mathematics, homotopical algebra is a collection of concepts comprising the nonabelian aspects of homological algebra as well as possibly the abelian aspects as special cases...
-
-
-