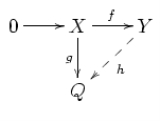
Injective module
Encyclopedia
In mathematics
, especially in the area of abstract algebra
known as module theory, an injective module is a module
Q that shares certain desirable properties with the Z-module Q of all rational number
s. Specifically, if Q is a submodule of some other module, then it is already a direct summand of that module; also, given a submodule of a module Y, then any module homomorphism from this submodule to Q can be extended to a homomorphism from all of Y to Q. This concept is dual to that of projective module
s. Injective modules were introduced in and are discussed in some detail in the textbook .
Injective modules have been heavily studied, and a variety of additional notions are defined in terms of them: Injective cogenerator
s are injective modules that faithfully represent the entire category of modules. Injective resolutions measure how far from injective a module is in terms of the injective dimension and represent modules in the derived category
. Injective hull
s are maximal essential extensions, and turn out to be minimal injective extensions. Over a Noetherian ring
, every injective module is uniquely a direct sum of indecomposable
modules, and their structure is well understood. An injective module over one ring, may not be injective over another, but there are well-understood methods of changing rings which handle special cases. Rings which are themselves injective modules have a number of interesting properties and include rings such as group ring
s of finite group
s over field
s. Injective modules include divisible group
s and are generalized by the notion of injective object
s in category theory
.
R is injective if it satisfies one (and therefore all) of the following equivalent conditions:
Injective right R-modules are defined in complete analogy.
Given a field
k, every k-vector space
Q is an injective k-module. Reason: if Q is a subspace of V, we can find a basis of Q and extend it to a basis of V. The new extending basis vectors span
a subspace K of V and V is the internal direct sum of Q and K. Note that the direct complement K of Q is not uniquely determined by Q, and likewise the extending map h in the above definition is typically not unique.
The rationals Q (with addition) form an injective abelian group (i.e. an injective Z-module). The factor group Q/Z and the circle group are also injective Z-modules. The factor group Z/nZ for n > 1 is injective as a Z/nZ-module, but not injective as an abelian group.
, the quotient module
K/R is also injective, and its indecomposable
summands are the localizations
 for the nonzero prime ideal
for the nonzero prime ideal
s . The zero ideal is also prime and corresponds to the injective K. In this way there is a 1-1 correspondence between prime ideals and indecomposable injective modules.
. The zero ideal is also prime and corresponds to the injective K. In this way there is a 1-1 correspondence between prime ideals and indecomposable injective modules.
A particularly rich theory is available for commutative
noetherian ring
s due to Eben Matlis
, . Every injective module is uniquely a direct sum of indecomposable injective modules, and the indecomposable injective modules are uniquely identified as the injective hulls of the quotients R/P where P varies over the prime spectrum of the ring. The injective hull of R/P as an R-module is canonically an RP module, and is the RP-injective hull of R/P. In other words, it suffices to consider local ring
s. The endomorphism ring
of the injective hull of R/P is the completion
 of R at P.
of R at P.
Two particularly instructive examples are the injective hull of the Z-module Z/pZ (the Prüfer group
), and the injective hull of the k[x]-module k (the ring of inverse polynomials). The latter is easily described as k(x)/k[x], but the form of the elements is quite transparent: The module has a basis consisting of "inverse monomials", that is x−n for n = 1, 2, …. Multiplication by scalars is as expected, and multiplication by x behaves normally except that x·x−1 = 0. The endomorphism ring is simply the ring of formal power series
.
and k a field with characteristic
0, then one shows in the theory of group representation
s that any subrepresentation of a given one is already a direct summand of the given one. Translated into module language, this means that all modules over the group algebra
kG are injective. If the characteristic of k is not zero, the following example may help.
If A is a unital associative algebra
over the field k with finite dimension over k, then Homk(−, k) is a duality between finitely generated left A-modules and finitely generated right A-modules. Therefore, the finitely generated injective left A-modules are precisely the modules of the form Homk(P, k) where P is a finitely generated projective right A-module. For symmetric algebras
, the duality is particularly well-behaved and projective modules and injective modules coincide.
For any Artinian ring
, just as for commutative ring
s, there is a 1-1 correspondence between prime ideals and indecomposable injective modules. The correspondence in this case is perhaps even simpler: a prime ideal is an annihilator of a unique simple module, and the corresponding indecomposable injective module is its injective hull
. For finite dimensional algebras over fields, these injective hulls are finitely-generated module
s .
of (even infinitely many) injective modules is injective; conversely, if a direct product of modules is injective, then each module is injective . Every direct sum of finitely many injective modules is injective. In general, submodules, factor modules, or infinite direct sums
of injective modules need not be injective. Every submodule of every injective module is injective if and only if the ring is Artinian
semisimple ; every factor module of every injective module is injective if and only if the ring is hereditary
, ; every infinite direct sum of injective modules is injective if and only if the ring is Noetherian
, .
I of R can be extended to all of R.
Using this criterion, one can show that Q is an injective abelian group
(i.e. an injective module over Z). More generally, an abelian group is injective if and only if it is divisible. More generally still: a module over a principal ideal domain
is injective if and only if it is divisible (the case of vector spaces is an example of this theorem, as every field is a principal ideal domain and every vector space is divisible). Over a general integral domain, we still have one implication: every injective module over an integral domain is divisible.
Baer's criterion has been refined in many ways , including a result of and that for a commutative Noetherian ring, it suffices to consider only prime ideal
s I. The dual of Baer's Criterion would give a simple test for projectivity, but even for the ring Z of integers, this becomes the unsolvable Whitehead problem
.
in the category of abelian groups
, which means that it is injective and any other module is contained in a suitably large product of copies of Q/Z. So in particular, every abelian group is subgroup of an injective one. It is quite significant that this is also true over any ring: every module is a submodule of an injective one, or "the category of left R-modules has enough injectives." To prove this, one uses the peculiar properties of the abelian group Q/Z to construct an injective cogenerator in the category of left R-modules.
For a left R-module M, the so called "character module" M+ = HomZ(M,Q/Z) is a right R-module that exhibits an interesting duality, not between injective modules and projective module
s, but between injective modules and flat module
s . For any ring R, a left R-module is flat if and only if its character module is injective. If R is left noetherian, then a left R-module is injective if and only if its character module is flat.
of the form
where the I j are injective. These injective resolutions can be used to define derived functor
s such as the Ext functor
.
of a module is essentially the smallest injective module containing the given one and was described in .
One can use injective hulls to define a minimal injective resolution. If each term of the injective resolution is the injective hull of the cokernel of the previous map, then the injective resolution has minimal length.
injective modules, .
Every indecomposable injective module has a local
endomorphism ring
. A module is called uniform if every two nontrivial submodules intersect nontrivially. For an injective module M the following are equivalent:
Over a Noetherian ring, every injective module is the direct sum of (uniquely determined) indecomposable injective modules. Over a commutative Noetherian ring, this gives a particularly nice understanding of all injective modules, described in .
s or quotient ring
s, especially for instance polynomial ring
s. In general, this is difficult, but a number of results are known, .
Let S and R be rings, and P be a left-R, right-S bimodule
that is flat
as a left-R module. For any injective right S-module M, the set of module homomorphisms HomS( P, M ) is an injective right R-module. For instance, if R is a subring of S such that S is a flat R-module, then every injective S-module is an injective R-module. In particular, if R is an integral domain and S its field of fractions
, then every vector space over S is an injective R-module. Similarly, every injective R[x]-module is an injective R-module.
For quotient rings R/I, the change of rings is also very clear. An R-module is an R/I-module precisely when it is annihilated by I. The submodule annI(M) = { m in M : im = 0 for all i in I } is a a left submodule of the left R-module M, and is the largest submodule of M that is an R/I-module. If M is an injective left R-module, then annI(M) is an injective left R/I-module. Applying this to R=Z, I=nZ and M=Q/Z, one gets the familiar fact that Z/nZ is injective as a module over itself. While it is easy to convert injective R-modules into injective R/I-modules, this process does not convert injective R-resolutions into injective R/I-resolutions, and the homology of the resulting complex is one of the early and fundamental areas of study of relative homological algebra.
The textbook has an erroneous proof that localization
preserves injectives, but a counterexample was given in .
and hence is a projective
as a module over itself, but it is rarer for a ring to be injective as a module over itself, . If a ring is injective over itself as a right module, then it is called a right self-injective ring. Every Frobenius algebra
is self-injective, but no integral domain that is not a field
is self-injective. Every proper quotient
of a Dedekind domain
is self-injective.
A right Noetherian
, right self-injective ring is called a quasi-Frobenius ring
, and is two-sided Artinian
and two-sided injective, . An important module theoretic property of quasi-Frobenius rings is that the projective modules are exactly the injective modules.
over a field, and taking R to be any ring containing every matrix which is zero in all but the last column, the injective hull of the right R-module R is S. For instance, one can take R to be the ring of all upper triangular matrices. However, it is not always the case that the injective hull of a ring has a ring structure, as an example in shows.
A large class of rings which do have ring structures on their injective hulls are the so-called non-singular rings, , including all reduced
commutative rings, that is commutative rings without nilpotent elements, . In particular, for an integral domain, one recalls the injective hull of the ring is the field of fractions
. The injective hulls of nonsingular rings provide the more general analogue of fields of fractions for non-commutative rings; compare to the more restrictive localization defined for Ore domains. This type of "ring of quotients" (as these more general "fields of fractions" are called) was pioneered in , and the connection to injective hulls was recognized in .
s in categories
more general than module categories, for instance in functor categories
or in categories of sheaves
of OX-modules over some ringed space
(X,OX). The following general definition is used: an object Q of the category C is injective if for any monomorphism
f : X → Y in C and any morphism g : X → Q there exists a morphism h : Y → Q with hf = g.
. Here a Z-module M is injective if and only if n⋅M = M for every nonzero integer n. Here the relationships between flat module
s, pure submodule
s, and injective modules is more clear, as it simply refers to certain divisibility properties of module elements by integers.
can extended to the whole module.
| volume=46 | pages=800–807 | issue=10}} | year=1960 | journal=Transactions of the American Mathematical Society
| volume=97 | pages=457–473 | issue=3 | publisher=Transactions of the American Mathematical Society, Vol. 97, No. 3 | jstor=1993382}} | year=1981 | journal=Journal of Algebra
| volume=69 | issue=2 | pages=416–425}} | year=1953 | journal=Archiv der Mathematik | volume=4 | pages=75–78 | issue=2}} | year=1963 | journal=Canadian Journal of Mathematics
| issn=0008-414X | volume=15 | pages=363–370 | url=http://www.cms.math.ca/cjm/v15/p363 | doi=10.4153/CJM-1963-041-4 }} | year=1958 | journal=Pacific Journal of Mathematics
| issn=0030-8730 | volume=8 | pages=511–528}} | year=1964 | journal=Canadian Mathematical Bulletin | issn=0008-4395 | volume=7 | pages=405–413 | doi=10.4153/CMB-1964-039-3}} | year=1959 | journal=Publicationes Mathematicae Debrecen
| issn=0033-3883 | volume=6 | pages=311–327}} | year=1981 | journal=Communications in Algebra | volume=9 | issue=9 | pages=989–999}} | year=1956 | journal=Osaka Journal of Mathematics | issn=0030-6126 | volume=8 | pages=1–18}} | year=1983 | journal=Communications in Algebra | volume=11 | issue=22 | pages=2495–2505}}
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in the area of abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
known as module theory, an injective module is a module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
Q that shares certain desirable properties with the Z-module Q of all rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s. Specifically, if Q is a submodule of some other module, then it is already a direct summand of that module; also, given a submodule of a module Y, then any module homomorphism from this submodule to Q can be extended to a homomorphism from all of Y to Q. This concept is dual to that of projective module
Projective module
In mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
s. Injective modules were introduced in and are discussed in some detail in the textbook .
Injective modules have been heavily studied, and a variety of additional notions are defined in terms of them: Injective cogenerator
Injective cogenerator
In category theory, the concept of an injective cogenerator is drawn from examples such as Pontryagin duality. Generators are objects which cover other objects as an approximation, and cogenerators are objects which envelope other objects as an approximation...
s are injective modules that faithfully represent the entire category of modules. Injective resolutions measure how far from injective a module is in terms of the injective dimension and represent modules in the derived category
Derived category
In mathematics, the derived category D of an abelian category C is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on C...
. Injective hull
Injective hull
In mathematics, especially in the area of abstract algebra known as module theory, the injective hull of a module is both the smallest injective module containing it and the largest essential extension of it...
s are maximal essential extensions, and turn out to be minimal injective extensions. Over a Noetherian ring
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
, every injective module is uniquely a direct sum of indecomposable
Indecomposable module
In abstract algebra, a module is indecomposable if it is non-zero and cannot be written as a direct sum of two non-zero submodules.Indecomposable is a weaker notion than simple module:simple means "no proper submodule" N...
modules, and their structure is well understood. An injective module over one ring, may not be injective over another, but there are well-understood methods of changing rings which handle special cases. Rings which are themselves injective modules have a number of interesting properties and include rings such as group ring
Group ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
s of finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
s over field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
s. Injective modules include divisible group
Divisible group
In mathematics, especially in the field of group theory, a divisible group is an abelian group in which every element can, in some sense, be divided by positive integers, or more accurately, every element is an nth multiple for each positive integer n...
s and are generalized by the notion of injective object
Injective object
In mathematics, especially in the field of category theory, the concept of injective object is a generalization of the concept of injective module. This concept is important in homotopy theory and in theory of model categories...
s in category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
.
Definition
A left module Q over the ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
R is injective if it satisfies one (and therefore all) of the following equivalent conditions:
- If Q is a submodule of some other left R-module M, then there exists another submodule K of M such that M is the internal direct sumDirect sum of modulesIn abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
of Q and K, i.e. Q + K = M and Q ∩ K = {0}. - Any short exact sequence 0 →Q → M → K → 0 of left R-modules splits.
- If X and Y are left R-modules and f : X → Y is an injective module homomorphism and g : X → Q is an arbitrary module homomorphism, then there exists a module homomorphism h : Y → Q such that hf = g, i.e. such that the following diagram commutesCommutative diagramIn mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
:
-
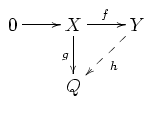
- The contravariant functor Hom(-,Q) from the categoryCategory theoryCategory theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
of left R-modules to the category of abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s is exactExact functorIn homological algebra, an exact functor is a functor, from some category to another, which preserves exact sequences. Exact functors are very convenient in algebraic calculations, roughly speaking because they can be applied to presentations of objects easily...
.
- The contravariant functor Hom(-,Q) from the category
Injective right R-modules are defined in complete analogy.
First examples
Trivially, the zero module {0} is injective.Given a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
k, every k-vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
Q is an injective k-module. Reason: if Q is a subspace of V, we can find a basis of Q and extend it to a basis of V. The new extending basis vectors span
Linear span
In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
a subspace K of V and V is the internal direct sum of Q and K. Note that the direct complement K of Q is not uniquely determined by Q, and likewise the extending map h in the above definition is typically not unique.
The rationals Q (with addition) form an injective abelian group (i.e. an injective Z-module). The factor group Q/Z and the circle group are also injective Z-modules. The factor group Z/nZ for n > 1 is injective as a Z/nZ-module, but not injective as an abelian group.
Commutative examples
More generally, for any integral domain R with field of fractions K, the R-module K is an injective R-module, and indeed the smallest injective R-module containing R. For any Dedekind domainDedekind domain
In abstract algebra, a Dedekind domain or Dedekind ring, named after Richard Dedekind, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily unique up to the order of the factors...
, the quotient module
Quotient module
In abstract algebra, given a module and a submodule, one can construct their quotient module. This construction, described below, is analogous to how one obtains the ring of integers modulo an integer n, see modular arithmetic...
K/R is also injective, and its indecomposable
Indecomposable module
In abstract algebra, a module is indecomposable if it is non-zero and cannot be written as a direct sum of two non-zero submodules.Indecomposable is a weaker notion than simple module:simple means "no proper submodule" N...
summands are the localizations
Localization of a ring
In abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
 for the nonzero prime ideal
for the nonzero prime idealPrime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
s
 . The zero ideal is also prime and corresponds to the injective K. In this way there is a 1-1 correspondence between prime ideals and indecomposable injective modules.
. The zero ideal is also prime and corresponds to the injective K. In this way there is a 1-1 correspondence between prime ideals and indecomposable injective modules.A particularly rich theory is available for commutative
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
noetherian ring
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
s due to Eben Matlis
Eben Matlis
Eben Matlis is a mathematician known for his contributions to the theory of rings and modules, especially for his work with injective modules over commutative Noetherian rings....
, . Every injective module is uniquely a direct sum of indecomposable injective modules, and the indecomposable injective modules are uniquely identified as the injective hulls of the quotients R/P where P varies over the prime spectrum of the ring. The injective hull of R/P as an R-module is canonically an RP module, and is the RP-injective hull of R/P. In other words, it suffices to consider local ring
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
s. The endomorphism ring
Endomorphism ring
In abstract algebra, one associates to certain objects a ring, the object's endomorphism ring, which encodes several internal properties of the object; this may be denoted End...
of the injective hull of R/P is the completion
Completion (ring theory)
In abstract algebra, a completion is any of several related functors on rings and modules that result in complete topological rings and modules. Completion is similar to localization, and together they are among the most basic tools in analysing commutative rings. Complete commutative rings have...
 of R at P.
of R at P.Two particularly instructive examples are the injective hull of the Z-module Z/pZ (the Prüfer group
Prüfer group
In mathematics, specifically in group theory, the Prüfer p-group or the p-quasicyclic group or p∞-group, Z, for a prime number p is the unique p-group in which every element has p pth roots. The group is named after Heinz Prüfer...
), and the injective hull of the k[x]-module k (the ring of inverse polynomials). The latter is easily described as k(x)/k[x], but the form of the elements is quite transparent: The module has a basis consisting of "inverse monomials", that is x−n for n = 1, 2, …. Multiplication by scalars is as expected, and multiplication by x behaves normally except that x·x−1 = 0. The endomorphism ring is simply the ring of formal power series
Formal power series
In mathematics, formal power series are a generalization of polynomials as formal objects, where the number of terms is allowed to be infinite; this implies giving up the possibility to substitute arbitrary values for indeterminates...
.
Artinian examples
If G is a finite groupFinite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
and k a field with characteristic
Characteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
0, then one shows in the theory of group representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
s that any subrepresentation of a given one is already a direct summand of the given one. Translated into module language, this means that all modules over the group algebra
Group algebra
In mathematics, the group algebra is any of various constructions to assign to a locally compact group an operator algebra , such that representations of the algebra are related to representations of the group...
kG are injective. If the characteristic of k is not zero, the following example may help.
If A is a unital associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
over the field k with finite dimension over k, then Homk(−, k) is a duality between finitely generated left A-modules and finitely generated right A-modules. Therefore, the finitely generated injective left A-modules are precisely the modules of the form Homk(P, k) where P is a finitely generated projective right A-module. For symmetric algebras
Frobenius algebra
In mathematics, especially in the fields of representation theory and module theory, a Frobenius algebra is a finite dimensional unital associative algebra with a special kind of bilinear form which gives the algebras particularly nice duality theories. Frobenius algebras began to be studied in...
, the duality is particularly well-behaved and projective modules and injective modules coincide.
For any Artinian ring
Artinian ring
In abstract algebra, an Artinian ring is a ring that satisfies the descending chain condition on ideals. They are also called Artin rings and are named after Emil Artin, who first discovered that the descending chain condition for ideals simultaneously generalizes finite rings and rings that are...
, just as for commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
s, there is a 1-1 correspondence between prime ideals and indecomposable injective modules. The correspondence in this case is perhaps even simpler: a prime ideal is an annihilator of a unique simple module, and the corresponding indecomposable injective module is its injective hull
Injective hull
In mathematics, especially in the area of abstract algebra known as module theory, the injective hull of a module is both the smallest injective module containing it and the largest essential extension of it...
. For finite dimensional algebras over fields, these injective hulls are finitely-generated module
Finitely-generated module
In mathematics, a finitely generated module is a module that has a finite generating set. A finitely generated R-module also may be called a finite R-module or finite over R....
s .
Submodules, quotients, products, and sums
Any productProduct (category theory)
In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
of (even infinitely many) injective modules is injective; conversely, if a direct product of modules is injective, then each module is injective . Every direct sum of finitely many injective modules is injective. In general, submodules, factor modules, or infinite direct sums
Direct sum of modules
In abstract algebra, the direct sum is a construction which combines several modules into a new, larger module. The result of the direct summation of modules is the "smallest general" module which contains the given modules as submodules...
of injective modules need not be injective. Every submodule of every injective module is injective if and only if the ring is Artinian
Artinian ring
In abstract algebra, an Artinian ring is a ring that satisfies the descending chain condition on ideals. They are also called Artin rings and are named after Emil Artin, who first discovered that the descending chain condition for ideals simultaneously generalizes finite rings and rings that are...
semisimple ; every factor module of every injective module is injective if and only if the ring is hereditary
Hereditary ring
In mathematics, especially in the area of abstract algebra known as module theory, a ring R is called hereditary if all submodules of projective modules over R are again projective...
, ; every infinite direct sum of injective modules is injective if and only if the ring is Noetherian
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
, .
Baer's criterion
In Baer's original paper, he proved a useful result, usually known as Baer's Criterion, for checking whether a module is injective: a left R-module Q is injective if and only if any homomorphism g : I → Q defined on a left idealIdeal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
I of R can be extended to all of R.
Using this criterion, one can show that Q is an injective abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
(i.e. an injective module over Z). More generally, an abelian group is injective if and only if it is divisible. More generally still: a module over a principal ideal domain
Principal ideal domain
In abstract algebra, a principal ideal domain, or PID, is an integral domain in which every ideal is principal, i.e., can be generated by a single element. More generally, a principal ideal ring is a nonzero commutative ring whose ideals are principal, although some authors refer to PIDs as...
is injective if and only if it is divisible (the case of vector spaces is an example of this theorem, as every field is a principal ideal domain and every vector space is divisible). Over a general integral domain, we still have one implication: every injective module over an integral domain is divisible.
Baer's criterion has been refined in many ways , including a result of and that for a commutative Noetherian ring, it suffices to consider only prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
s I. The dual of Baer's Criterion would give a simple test for projectivity, but even for the ring Z of integers, this becomes the unsolvable Whitehead problem
Whitehead problem
In group theory, a branch of abstract algebra, the Whitehead problem is the following question:Shelah proved that Whitehead's problem is undecidable within standard ZFC set theory.-Refinement:...
.
Injective cogenerators
Maybe the most important injective module is the abelian group Q/Z. It is an injective cogeneratorInjective cogenerator
In category theory, the concept of an injective cogenerator is drawn from examples such as Pontryagin duality. Generators are objects which cover other objects as an approximation, and cogenerators are objects which envelope other objects as an approximation...
in the category of abelian groups
Category of abelian groups
In mathematics, the category Ab has the abelian groups as objects and group homomorphisms as morphisms. This is the prototype of an abelian category....
, which means that it is injective and any other module is contained in a suitably large product of copies of Q/Z. So in particular, every abelian group is subgroup of an injective one. It is quite significant that this is also true over any ring: every module is a submodule of an injective one, or "the category of left R-modules has enough injectives." To prove this, one uses the peculiar properties of the abelian group Q/Z to construct an injective cogenerator in the category of left R-modules.
For a left R-module M, the so called "character module" M+ = HomZ(M,Q/Z) is a right R-module that exhibits an interesting duality, not between injective modules and projective module
Projective module
In mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
s, but between injective modules and flat module
Flat module
In Homological algebra, and algebraic geometry, a flat module over a ring R is an R-module M such that taking the tensor product over R with M preserves exact sequences. A module is faithfully flat if taking the tensor product with a sequence produces an exact sequence if and only if the original...
s . For any ring R, a left R-module is flat if and only if its character module is injective. If R is left noetherian, then a left R-module is injective if and only if its character module is flat.
Injective resolutions
Every module M also has an injective resolution: an exact sequenceExact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
of the form
- 0 → M → I0 → I1 → I2 → ...
where the I j are injective. These injective resolutions can be used to define derived functor
Derived functor
In mathematics, certain functors may be derived to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics.- Motivation :...
s such as the Ext functor
Ext functor
In mathematics, the Ext functors of homological algebra are derived functors of Hom functors. They were first used in algebraic topology, but are common in many areas of mathematics.- Definition and computation :...
.
Injective dimension
Injective resolutions are also used to define the injective dimension of a module, . The injective dimension is the length of the shortest injective resolution ending in zeros, if such a finite resolution exists, otherwise the injective dimension is ∞. Equivalently, the injective dimension is the minimal integer (if there is such, otherwise ∞) n such that Ext(–,M) = 0 for all N > n.Injective hulls
The injective hullInjective hull
In mathematics, especially in the area of abstract algebra known as module theory, the injective hull of a module is both the smallest injective module containing it and the largest essential extension of it...
of a module is essentially the smallest injective module containing the given one and was described in .
One can use injective hulls to define a minimal injective resolution. If each term of the injective resolution is the injective hull of the cokernel of the previous map, then the injective resolution has minimal length.
Indecomposables
Every injective submodule of an injective module is a direct summand, so it is important to understand indecomposableIndecomposable module
In abstract algebra, a module is indecomposable if it is non-zero and cannot be written as a direct sum of two non-zero submodules.Indecomposable is a weaker notion than simple module:simple means "no proper submodule" N...
injective modules, .
Every indecomposable injective module has a local
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
endomorphism ring
Endomorphism ring
In abstract algebra, one associates to certain objects a ring, the object's endomorphism ring, which encodes several internal properties of the object; this may be denoted End...
. A module is called uniform if every two nontrivial submodules intersect nontrivially. For an injective module M the following are equivalent:
- M is indecomposable
- M is nonzero and is the injective hull of every nonzero submodule
- M is uniform
- M is the injective hull of a uniform module
- M is the injective hull of a uniform cyclic moduleCyclic moduleIn mathematics, more specifically in ring theory, a cyclic module is a module over a ring which is generated by one element. The term is by analogy with cyclic groups, that is groups which are generated by one element.- Definition :...
- M has a local endomorphism ring
Over a Noetherian ring, every injective module is the direct sum of (uniquely determined) indecomposable injective modules. Over a commutative Noetherian ring, this gives a particularly nice understanding of all injective modules, described in .
Change of rings
It is important to be able to consider modules over subringSubring
In mathematics, a subring of R is a subset of a ring, is itself a ring with the restrictions of the binary operations of addition and multiplication of R, and which contains the multiplicative identity of R...
s or quotient ring
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
s, especially for instance polynomial ring
Polynomial ring
In mathematics, especially in the field of abstract algebra, a polynomial ring is a ring formed from the set of polynomials in one or more variables with coefficients in another ring. Polynomial rings have influenced much of mathematics, from the Hilbert basis theorem, to the construction of...
s. In general, this is difficult, but a number of results are known, .
Let S and R be rings, and P be a left-R, right-S bimodule
Bimodule
In abstract algebra a bimodule is an abelian group that is both a left and a right module, such that the left and right multiplications are compatible...
that is flat
Flat module
In Homological algebra, and algebraic geometry, a flat module over a ring R is an R-module M such that taking the tensor product over R with M preserves exact sequences. A module is faithfully flat if taking the tensor product with a sequence produces an exact sequence if and only if the original...
as a left-R module. For any injective right S-module M, the set of module homomorphisms HomS( P, M ) is an injective right R-module. For instance, if R is a subring of S such that S is a flat R-module, then every injective S-module is an injective R-module. In particular, if R is an integral domain and S its field of fractions
Field of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
, then every vector space over S is an injective R-module. Similarly, every injective R[x]-module is an injective R-module.
For quotient rings R/I, the change of rings is also very clear. An R-module is an R/I-module precisely when it is annihilated by I. The submodule annI(M) = { m in M : im = 0 for all i in I } is a a left submodule of the left R-module M, and is the largest submodule of M that is an R/I-module. If M is an injective left R-module, then annI(M) is an injective left R/I-module. Applying this to R=Z, I=nZ and M=Q/Z, one gets the familiar fact that Z/nZ is injective as a module over itself. While it is easy to convert injective R-modules into injective R/I-modules, this process does not convert injective R-resolutions into injective R/I-resolutions, and the homology of the resulting complex is one of the early and fundamental areas of study of relative homological algebra.
The textbook has an erroneous proof that localization
Localization of a ring
In abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
preserves injectives, but a counterexample was given in .
Self-injective rings
Every ring with unity is a free moduleFree module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
and hence is a projective
Projective module
In mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
as a module over itself, but it is rarer for a ring to be injective as a module over itself, . If a ring is injective over itself as a right module, then it is called a right self-injective ring. Every Frobenius algebra
Frobenius algebra
In mathematics, especially in the fields of representation theory and module theory, a Frobenius algebra is a finite dimensional unital associative algebra with a special kind of bilinear form which gives the algebras particularly nice duality theories. Frobenius algebras began to be studied in...
is self-injective, but no integral domain that is not a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
is self-injective. Every proper quotient
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
of a Dedekind domain
Dedekind domain
In abstract algebra, a Dedekind domain or Dedekind ring, named after Richard Dedekind, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily unique up to the order of the factors...
is self-injective.
A right Noetherian
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
, right self-injective ring is called a quasi-Frobenius ring
Quasi-Frobenius ring
In ring theory, the class of Frobenius rings and their generalizations are the extension of work done on Frobenius algebras. Perhaps the most important generalization is that of quasi-Frobenius rings , which are in turn generalized by right pseudo-Frobenius rings and right finitely...
, and is two-sided Artinian
Artinian ring
In abstract algebra, an Artinian ring is a ring that satisfies the descending chain condition on ideals. They are also called Artin rings and are named after Emil Artin, who first discovered that the descending chain condition for ideals simultaneously generalizes finite rings and rings that are...
and two-sided injective, . An important module theoretic property of quasi-Frobenius rings is that the projective modules are exactly the injective modules.
Ring structure
In many cases, for R a subring of a self-injective ring S, the injective hull of R will also have a ring structure, . For instance, taking S to be a full matrix ringMatrix ring
In abstract algebra, a matrix ring is any collection of matrices forming a ring under matrix addition and matrix multiplication. The set of n×n matrices with entries from another ring is a matrix ring, as well as some subsets of infinite matrices which form infinite matrix rings...
over a field, and taking R to be any ring containing every matrix which is zero in all but the last column, the injective hull of the right R-module R is S. For instance, one can take R to be the ring of all upper triangular matrices. However, it is not always the case that the injective hull of a ring has a ring structure, as an example in shows.
A large class of rings which do have ring structures on their injective hulls are the so-called non-singular rings, , including all reduced
Reduced ring
In ring theory, a ring R is called a reduced ring if it has no non-zero nilpotent elements. Equivalently, a ring is reduced if it has no non-zero elements with square zero, that is, x2 = 0 implies x = 0...
commutative rings, that is commutative rings without nilpotent elements, . In particular, for an integral domain, one recalls the injective hull of the ring is the field of fractions
Field of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
. The injective hulls of nonsingular rings provide the more general analogue of fields of fractions for non-commutative rings; compare to the more restrictive localization defined for Ore domains. This type of "ring of quotients" (as these more general "fields of fractions" are called) was pioneered in , and the connection to injective hulls was recognized in .
Injective objects
One also talks about injective objectInjective object
In mathematics, especially in the field of category theory, the concept of injective object is a generalization of the concept of injective module. This concept is important in homotopy theory and in theory of model categories...
s in categories
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
more general than module categories, for instance in functor categories
Functor category
In category theory, a branch of mathematics, the functors between two given categories form a category, where the objects are the functors and the morphisms are natural transformations between the functors...
or in categories of sheaves
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
of OX-modules over some ringed space
Ringed space
In mathematics, a ringed space is, intuitively speaking, a space together with a collection of commutative rings, the elements of which are "functions" on each open set of the space...
(X,OX). The following general definition is used: an object Q of the category C is injective if for any monomorphism
Monomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
f : X → Y in C and any morphism g : X → Q there exists a morphism h : Y → Q with hf = g.
Divisible groups
The notion of injective object in the category of abelian groups was studied somewhat independently of injective modules under the term divisible groupDivisible group
In mathematics, especially in the field of group theory, a divisible group is an abelian group in which every element can, in some sense, be divided by positive integers, or more accurately, every element is an nth multiple for each positive integer n...
. Here a Z-module M is injective if and only if n⋅M = M for every nonzero integer n. Here the relationships between flat module
Flat module
In Homological algebra, and algebraic geometry, a flat module over a ring R is an R-module M such that taking the tensor product over R with M preserves exact sequences. A module is faithfully flat if taking the tensor product with a sequence produces an exact sequence if and only if the original...
s, pure submodule
Pure submodule
In mathematics, especially in the field of module theory, the concept of pure submodule provides a generalization of direct summand, a type of particularly well-behaved piece of a module. Pure modules are complementary to flat modules and generalize Prüfer's notion of pure subgroups...
s, and injective modules is more clear, as it simply refers to certain divisibility properties of module elements by integers.
Pure injectives
In relative homological algebra, the extension property of homomorphisms may be required only for certain submodules, rather than for all. For instance, a pure injective module is a module in which a homomorphism from a pure submodulePure submodule
In mathematics, especially in the field of module theory, the concept of pure submodule provides a generalization of direct summand, a type of particularly well-behaved piece of a module. Pure modules are complementary to flat modules and generalize Prüfer's notion of pure subgroups...
can extended to the whole module.
Textbooks
| year=2000 | volume=30}} | year=1991 | volume=147}} | year=1999}} | year=1979 | volume=85}}Primary sources
| year=1940 | journal=Bulletin of the American Mathematical SocietyBulletin of the American Mathematical Society
The Bulletin of the American Mathematical Society is a quarterly mathematical journal published by the American Mathematical Society...
| volume=46 | pages=800–807 | issue=10}} | year=1960 | journal=Transactions of the American Mathematical Society
Transactions of the American Mathematical Society
Transactions of the American Mathematical Society is a monthly mathematics journal published by the American Mathematical Society. It started in 1900...
| volume=97 | pages=457–473 | issue=3 | publisher=Transactions of the American Mathematical Society, Vol. 97, No. 3 | jstor=1993382}} | year=1981 | journal=Journal of Algebra
Journal of Algebra
Journal of Algebra is a leading international mathematical research journal in algebra. An imprint of Academic Press, it is presently published by Elsevier. Journal of Algebra was founded by Graham Higman, who was its editor from 1964 to 1984. From 1985 until 2000, Walter Feit served as its...
| volume=69 | issue=2 | pages=416–425}} | year=1953 | journal=Archiv der Mathematik | volume=4 | pages=75–78 | issue=2}} | year=1963 | journal=Canadian Journal of Mathematics
Canadian Journal of Mathematics
The Canadian Journal of Mathematics is a bimonthly mathematics journal published by the Canadian Mathematical Society. It was established in 1949 by H.S.M. Coxeter and G. de B. Robinson. The current editors of the journal are Henry Kim and Robert McCann. The journal publishes articles in all...
| issn=0008-414X | volume=15 | pages=363–370 | url=http://www.cms.math.ca/cjm/v15/p363 | doi=10.4153/CJM-1963-041-4 }} | year=1958 | journal=Pacific Journal of Mathematics
Pacific Journal of Mathematics
The Pacific Journal of Mathematics is a mathematics research journal supported by a number of American, Asian and Australian universities and research institutes, and currently published on their behalf by Mathematical Sciences Publishers, a non-profit academic publishing organisation.It was...
| issn=0030-8730 | volume=8 | pages=511–528}} | year=1964 | journal=Canadian Mathematical Bulletin | issn=0008-4395 | volume=7 | pages=405–413 | doi=10.4153/CMB-1964-039-3}} | year=1959 | journal=Publicationes Mathematicae Debrecen
Publicationes Mathematicae Debrecen
Publicationes Mathematicae Debrecen is a Hungarian mathematical journal, edited and published in Debrecen, at the Mathematical Institute of the University of Debrecen. It was founded by Alfréd Rényi, Tibor Szele, and Ottó Varga in 1950. The current editor-in-chief is Lajos...
| issn=0033-3883 | volume=6 | pages=311–327}} | year=1981 | journal=Communications in Algebra | volume=9 | issue=9 | pages=989–999}} | year=1956 | journal=Osaka Journal of Mathematics | issn=0030-6126 | volume=8 | pages=1–18}} | year=1983 | journal=Communications in Algebra | volume=11 | issue=22 | pages=2495–2505}}

