
Modular lattice
Encyclopedia
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
, a modular lattice is a lattice
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
that satisfies the following self-dual condition:
Modular law: x ≤ b implies x ∨ (a ∧ b) = (x ∨ a) ∧ b,
where ≤ is the partial order, and ∨ and ∧ (called join and meet
Join and meet
In mathematics, join and meet are dual binary operations on the elements of a partially ordered set. A join on a set is defined as the supremum with respect to a partial order on the set, provided a supremum exists...
respectively) are the operations of the lattice. Modular lattices arise naturally in algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
and in many other areas of mathematics. For example, the subspaces of a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
(and more generally the submodules of a module over a ring) form a modular lattice.
Every distributive
Distributive lattice
In mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...
lattice is modular.
In a not necessarily modular lattice, there may still be elements b for which the modular law holds in connection with arbitrary elements a and x (≤ b). Such an element is called a modular element. Even more generally, the modular law may hold for a fixed pair (a, b). Such a pair is called a modular pair, and there are various generalizations of modularity related to this notion and to semimodularity
Semimodular lattice
In the branch of mathematics known as order theory, a semimodular lattice, is a lattice that satisfies the following condition:Semimodular law: a ∧ b ...
.
Introduction
The modular law can be seen (and memorized) as a restricted associative lawAssociativity
In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...
that connects the two lattice operations similarly to the way in which the associative law λ(μx) = (λμ)x for vector spaces connects multiplication in the field and scalar multiplication. The restriction x ≤ b is clearly necessary, since it follows from x ∨ (a ∧ b) = (x ∨ a) ∧ b.
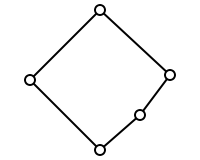
Modular law (variant): x ≤ b implies x ∨ (a ∧ b) ≥ (x ∨ a) ∧ b.
By substituting x with x ∧ b, the modular law can be expressed as an equation that is required to hold unconditionally, as follows:
Modular identity: (x ∧ b) ∨ (a ∧ b) = [(x ∧ b) ∨ a] ∧ b.
This shows that, using terminology from universal algebra
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
, the modular lattices form a subvariety of the variety
Variety (universal algebra)
In mathematics, specifically universal algebra, a variety of algebras is the class of all algebraic structures of a given signature satisfying a given set of identities. Equivalently, a variety is a class of algebraic structures of the same signature which is closed under the taking of homomorphic...
of lattices. Therefore all homomorphic images, sublattices and direct products of modular lattices are again modular.
The smallest non-modular lattice is the "pentagon" lattice N5 consisting of five elements 0,1,x,a,b such that 0 < x < b < 1, 0 < a < 1, and a is not comparable to x or to b. For this lattice x ∨ (a ∧ b) = x ∨ 0 = x < b = 1 ∧ b = (x ∨ a) ∧ b holds, contradicting the modular law. Every non-modular lattice contains a copy of N5 as a sublattice.
Modular lattices are sometimes called Dedekind lattices after Richard Dedekind
Richard Dedekind
Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
, who discovered the modular identity.
Diamond isomorphism theorem
For any two elements a,b of a modular lattice, one can consider the intervals [a ∧ b, b] and [a, a ∨ b]. They are connected by order-preserving maps-
- φ: [a ∧ b, b] → [a, a ∨ b] and
- ψ: [a, a ∨ b] → [a ∧ b, b]
that are defined by φ(x) = x ∨ a and ψ(x) = x ∧ b.
The composition ψφ is an order-preserving map from the interval [a ∧ b, b] to itself which also satisfies the inequality ψ(φ(x)) = (x ∨ a) ∧ b ≥ x. The example shows that this inequality can be strict in general. In a modular lattice, however, equality holds. Since the dual of a modular lattice is again modular, φψ is also the identity on [a, a ∨ b], and therefore the two maps φ and ψ are isomorphisms between these two intervals. This result is sometimes called the diamond isomorphism theorem for modular lattices. A lattice is modular if and only if the diamond isomorphism theorem holds for every pair of elements.
The diamond isomorphism theorem for modular lattices is analogous to the third isomorphism theorem
Isomorphism theorem
In mathematics, specifically abstract algebra, the isomorphism theorems are three theorems that describe the relationship between quotients, homomorphisms, and subobjects. Versions of the theorems exist for groups, rings, vector spaces, modules, Lie algebras, and various other algebraic structures...
in algebra, and it is a generalization of the lattice theorem
Lattice theorem
In mathematics, the lattice theorem, sometimes referred to as the fourth isomorphism theorem or the correspondence theorem, states that if N is a normal subgroup of a group G, then there exists a bijection from the set of all subgroups A of G such that A contains N, onto the set of all subgroups...
.
Modular pairs and related notions
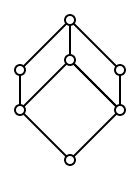
A lattice with the property that if (a, b) is a modular pair, then (b, a) is also a modular pair is called an M-symmetric lattice. Since a lattice is modular if and only if all pairs of elements are modular, clearly every modular lattice is M-symmetric. In the lattice N5 described above, the pair (b, a) is modular, but the pair (a, b) is not. Therefore N5 is not M-symmetric. The centred hexagon lattice S7 is M-symmetric but not modular. Since N5 is a sublattice of S7, it follows that the M-symmetric lattices do not form a subvariety of the variety of lattices.
M-symmetry is not a self-dual notion. A dual modular pair is a pair which is modular in the dual
Duality (order theory)
In the mathematical area of order theory, every partially ordered set P gives rise to a dual partially ordered set which is often denoted by Pop or Pd. This dual order Pop is defined to be the set with the inverse order, i.e. x ≤ y holds in Pop if and only if y ≤ x holds in P...
lattice, and a lattice is called dually M-symmetric or M*-symmetric if its dual is M-symmetric. It can be shown that a finite lattice is modular if and only if it is M-symmetric and M*-symmetric. The same equivalence holds for infinite lattices which satisfy the ascending chain condition
Ascending chain condition
The ascending chain condition and descending chain condition are finiteness properties satisfied by some algebraic structures, most importantly, ideals in certain commutative rings...
(or the descending chain condition).
Several less important notions are also closely related. A lattice is cross-symmetric if for every modular pair (a, b) the pair (b, a) is dually modular. Cross-symmetry implies M-symmetry but not M*-symmetry. Therefore cross-symmetry is not equivalent to dual cross-symmetry. A lattice with a least element 0 is ⊥-symmetric if for every modular pair (a, b) satisfying a ∧ b = 0 the pair (b, a) is also modular.
History
The definition of modularity is due to Richard DedekindRichard Dedekind
Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
, who published most of the relevant papers after his retirement.
In a paper published in 1894 he studied lattices, which he called dual groups as part of his "algebra of modules" and observed that ideals satisfy what we now call the modular law. He also observed that for lattices in general, the modular law is equivalent to its dual.
In another paper in 1897, Dedekind studied the lattice of divisors with gcd and lcm as operations, so that the lattice order is given by divisibility.
In a digression he introduced and studied lattices formally in a general context. He observed that the lattice of submodules of a module satisfies the modular identity. He called such lattices dual groups of module type . He also proved that the modular identity and its dual are equivalent.
In the same paper, Dedekind observed further that any lattice of ideals of a ring satisfies the following stronger form of the modular identity, which is also self-dual:
- (x ∧ b) ∨ (a ∧ b) = [x ∨ a] ∧ b.
He called lattices that satisfy this identity dual groups of ideal type . In modern literature, they are more commonly referred to as distributive lattices
Distributive lattice
In mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...
.
He gave examples of a lattice that is not modular and of a modular lattice that is not of ideal type.
A paper published by Dedekind in 1900 had lattices as its central topic: He described the free modular lattice generated by three elements, a lattice with 28 elements.
See also
- Young–Fibonacci latticeYoung–Fibonacci latticeIn mathematics, the Young–Fibonacci graph and Young–Fibonacci lattice, named after Alfred Young and Leonardo Fibonacci, are two closely related structures involving sequences of the digits 1 and 2...
, an infinite modular lattice defined on strings of the digits 1 and 2. - Orthomodular lattice

