Annihilator (ring theory)
Encyclopedia
In mathematics
, specifically module theory, annihilators are a concept that generalizes torsion and orthogonal complement.
, and let M be a left R-module
. Choose a nonempty subset S of M. The annihilator, denoted AnnR(S), of S is the set of all elements r in R such that for each s in S, rs = 0: In set notation,
It is the set of all elements of R that "annihilate" S (the elements for which S is torsion). Subsets of right modules may be used as well, after the modification of "sr =0" in the definition.
The annihilator of a single element x is usually written AnnR(x) instead of AnnR({x}). If the ring R can be understood from the context, the subscript R can be omitted.
Since S may be taken to be a subset of R itself, and R is both a right and a left R module, the notation must be modified slightly to indicate the left or right side. Usually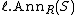 and
and 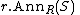 or some similar subscript scheme are used to indicate the left and right annihilators, if necessary.
or some similar subscript scheme are used to indicate the left and right annihilators, if necessary.
If M is an R module and AnnR(M) =0, then M is called a faithful module.
If S is a submodule of M, then AnnR(x) is even a two-sided ideal: (ac)s = a(cs) = 0, since cs is another element of S.
If S is a subset of M and N is the submodule of M generated by S, then in general AnnR(N) is a subset of AnnR(S), but they are not necessarily equal. If R is commutative, then it is easy to check that equality holds.
M may be also viewed as a R/AnnR(M)-module using the action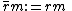 . Incidentally, it is not always possible to make an R module into an R/I module this way, but if the ideal I is a subset of the annihilator of M, then this action is well defined. Considered as an R/AnnR(M)-module, M is automatically a faithful module.
. Incidentally, it is not always possible to make an R module into an R/I module this way, but if the ideal I is a subset of the annihilator of M, then this action is well defined. Considered as an R/AnnR(M)-module, M is automatically a faithful module.
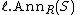 where S is a subset of R comprise a complete lattice
where S is a subset of R comprise a complete lattice
when partially ordered by inclusion. It is interesting to study rings for which this lattice (or its right counterpart) satisfy the ascending chain condition
or descending chain condition.
Denote the lattice of left annihilator ideals of R as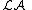 and the lattice of right annihilator ideals of R as
and the lattice of right annihilator ideals of R as 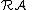 . It is known that
. It is known that 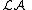 satisfies the A.C.C. if and only if
satisfies the A.C.C. if and only if 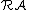 satisfies the D.C.C., and symmetrically
satisfies the D.C.C., and symmetrically 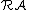 satisfies the A.C.C. if and only if
satisfies the A.C.C. if and only if 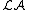 satisfies the D.C.C. If either lattice has either of these chain conditions, then R has no infinite orthogonal sets of idempotents.
satisfies the D.C.C. If either lattice has either of these chain conditions, then R has no infinite orthogonal sets of idempotents.
If R is a ring for which satisfies the A.C.C. and RR has finite uniform dimension, then R is called a left Goldie ring.
satisfies the A.C.C. and RR has finite uniform dimension, then R is called a left Goldie ring.
More generally, given a bilinear
map of modules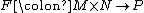 , the annihilator of a subset
, the annihilator of a subset 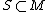 is the set of all elements in
is the set of all elements in 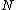 that annihilate
that annihilate 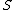 :
: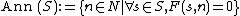
Conversely, given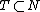 , one can define an annihilator as a subset of
, one can define an annihilator as a subset of 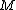 .
.
The annihilator gives a Galois connection
between subsets of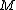 and
and 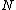 , and the associated closure operator
, and the associated closure operator
is stronger than the span.
In particular:
An important special case is in the presence of a nondegenerate form on a vector space, particularly an inner product: then the annihilator associated to the map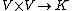 is called the orthogonal complement.
is called the orthogonal complement.
(Here we allow zero to be a zero divisor.)
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically module theory, annihilators are a concept that generalizes torsion and orthogonal complement.
Definitions
Let R be a ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, and let M be a left R-module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
. Choose a nonempty subset S of M. The annihilator, denoted AnnR(S), of S is the set of all elements r in R such that for each s in S, rs = 0: In set notation,

It is the set of all elements of R that "annihilate" S (the elements for which S is torsion). Subsets of right modules may be used as well, after the modification of "sr =0" in the definition.
The annihilator of a single element x is usually written AnnR(x) instead of AnnR({x}). If the ring R can be understood from the context, the subscript R can be omitted.
Since S may be taken to be a subset of R itself, and R is both a right and a left R module, the notation must be modified slightly to indicate the left or right side. Usually
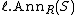 and
and 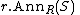 or some similar subscript scheme are used to indicate the left and right annihilators, if necessary.
or some similar subscript scheme are used to indicate the left and right annihilators, if necessary.If M is an R module and AnnR(M) =0, then M is called a faithful module.
Properties
If S is a subset of a left R module M, then Ann(S) left ideal of R. The proof is straightforward: If a and b both annihilate S, then for each s in S, (a + b)s = as + bs = 0, and for any r in R, (ra)s = r(as) = r0 = 0. (A similar proof follows for subsets of right modules to show that the annihilator is a right ideal.)If S is a submodule of M, then AnnR(x) is even a two-sided ideal: (ac)s = a(cs) = 0, since cs is another element of S.
If S is a subset of M and N is the submodule of M generated by S, then in general AnnR(N) is a subset of AnnR(S), but they are not necessarily equal. If R is commutative, then it is easy to check that equality holds.
M may be also viewed as a R/AnnR(M)-module using the action
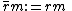 . Incidentally, it is not always possible to make an R module into an R/I module this way, but if the ideal I is a subset of the annihilator of M, then this action is well defined. Considered as an R/AnnR(M)-module, M is automatically a faithful module.
. Incidentally, it is not always possible to make an R module into an R/I module this way, but if the ideal I is a subset of the annihilator of M, then this action is well defined. Considered as an R/AnnR(M)-module, M is automatically a faithful module.Chain conditions on annihilator ideals
The lattice of ideals of the form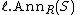 where S is a subset of R comprise a complete lattice
where S is a subset of R comprise a complete latticeComplete lattice
In mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum and an infimum . Complete lattices appear in many applications in mathematics and computer science...
when partially ordered by inclusion. It is interesting to study rings for which this lattice (or its right counterpart) satisfy the ascending chain condition
Ascending chain condition
The ascending chain condition and descending chain condition are finiteness properties satisfied by some algebraic structures, most importantly, ideals in certain commutative rings...
or descending chain condition.
Denote the lattice of left annihilator ideals of R as
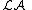 and the lattice of right annihilator ideals of R as
and the lattice of right annihilator ideals of R as 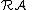 . It is known that
. It is known that 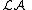 satisfies the A.C.C. if and only if
satisfies the A.C.C. if and only if 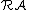 satisfies the D.C.C., and symmetrically
satisfies the D.C.C., and symmetrically 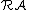 satisfies the A.C.C. if and only if
satisfies the A.C.C. if and only if 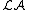 satisfies the D.C.C. If either lattice has either of these chain conditions, then R has no infinite orthogonal sets of idempotents.
satisfies the D.C.C. If either lattice has either of these chain conditions, then R has no infinite orthogonal sets of idempotents. If R is a ring for which
 satisfies the A.C.C. and RR has finite uniform dimension, then R is called a left Goldie ring.
satisfies the A.C.C. and RR has finite uniform dimension, then R is called a left Goldie ring. Category theoretic description for commutative rings
When R is commutative and M is an R-module, we may describe AnnR(M) as the kernel of the action map R→EndR(M) determined by the adjunct map of the identity M→M along the Hom-tensor adjunction.More generally, given a bilinear
Bilinear
Bilinear may refer to:* Bilinear sampling, a method in computer graphics for choosing the color of a texture* Bilinear form* Bilinear interpolation* Bilinear map, a type of mathematical function between vector spaces...
map of modules
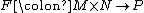 , the annihilator of a subset
, the annihilator of a subset 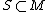 is the set of all elements in
is the set of all elements in 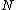 that annihilate
that annihilate 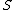 :
: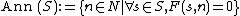
Conversely, given
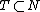 , one can define an annihilator as a subset of
, one can define an annihilator as a subset of 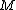 .
.The annihilator gives a Galois connection
Galois connection
In mathematics, especially in order theory, a Galois connection is a particular correspondence between two partially ordered sets . The same notion can also be defined on preordered sets or classes; this article presents the common case of posets. Galois connections generalize the correspondence...
between subsets of
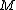 and
and 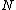 , and the associated closure operator
, and the associated closure operatorClosure operator
In mathematics, a closure operator on a set S is a function cl: P → P from the power set of S to itself which satisfies the following conditions for all sets X,Y ⊆ S....
is stronger than the span.
In particular:
- annihilators are submodules
-

-
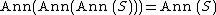
An important special case is in the presence of a nondegenerate form on a vector space, particularly an inner product: then the annihilator associated to the map
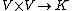 is called the orthogonal complement.
is called the orthogonal complement.Relations to other properties of rings
- Annihilators are used to define left Rickart rings and Baer ringBaer ringIn abstract algebra and functional analysis, Baer rings, Baer *-rings, Rickart rings, Rickart *-rings, and AW* algebras are various attempts to give an algebraic analogue of von Neumann algebras, using axioms about annihilators of various sets.Any von Neumann algebra is a Baer *-ring, and much of...
s. - The set of (left) zero divisorZero divisorIn abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
s DS of S can be written as
(Here we allow zero to be a zero divisor.)
- In particular DS is the set of (left) zero divisors of R when S = R and R acts on itself as a left R-module.
- When R is commutative, the set DR is precisely equal to the union of the minimal prime ideals of R.