Ringed space
Encyclopedia
In mathematics
, a ringed space is, intuitively speaking, a space together with a collection of commutative ring
s, the elements of which are "functions" on each open set
of the space. Ringed spaces appear throughout analysis
and are also used to define the scheme
s of algebraic geometry
.
X together with a sheaf
of rings OX on X. The sheaf OX is called the structure sheaf of X.
A locally ringed space is a ringed space (X, OX) such that all stalks of OX are local ring
s (i.e. they have unique maximal ideal
s). Note that it is not required that OX(U) be a local ring for every open set U. In fact, that is almost never going to be the case.
s on open subsets of X (there may exist continuous functions over open subsets of X which are not the restriction of any continuous function over X). The stalk
at a point x can be thought of as the set of all germ
s of continuous functions at x; this is a local ring with maximal ideal
consisting of those germs whose value at x is 0.
If X is a manifold
with some extra structure, we can also take the sheaf of differentiable, or complex-analytic
functions. Both of these give rise to locally ringed spaces.
If X is an algebraic variety
carrying the Zariski topology
, we can define a locally ringed space by taking OX(U) to be the ring of rational function
s defined on the Zariski-open set U which do not blow up (become infinite) within U. The important generalization of this example is that of the spectrum
of any commutative ring; these spectra are also locally ringed spaces. Schemes
are locally ringed spaces obtained by "gluing together" spectra of commutative rings.
of ringed spaces is a continuous map between their underlying topological spaces together with (essentially) a morphism between their structure sheaves. Explicitly, a morphism from (X, OX) to (Y, OY) is given by the following data:
There is an additional requirement for morphisms between locally ringed spaces:
Two morphisms can be composed to form a new morphism, and we obtain the category
of ringed spaces and the category of locally ringed spaces. Isomorphism
s in these categories are defined as usual.
s. Let X be locally ringed space with structure sheaf OX; we want to define the tangent space Tx at the point x ∈ X. Take the local ring (stalk) Rx at the point x, with maximal ideal mx. Then kx := Rx/mx is a field
and mx/mx2 is a vector space
over that field (the cotangent space
). The tangent space Tx is defined as the dual
of this vector space.
The idea is the following: a tangent vector at x should tell you how to "differentiate" "functions" at x, i.e. the elements of Rx. Now it is enough to know how to differentiate functions whose value at x is zero, since all other functions differ from these only by a constant, and we know how to differentiate constants. So we only need to worry about mx. Furthermore, if two functions are given with value zero at x, then their product has derivative 0 at x, by the product rule
. So we only need to know how to assign "numbers" to the elements of mx/mx2, and this is what the dual space does.
of modules on X occur in the applications, the OX-modules. To define them, consider a sheaf F of abelian group
s on X. If F(U) is a module
over the ring OX(U) for every open set U in X, and the restriction maps are compatible with the module structure, then we call F an OX-module. In this case, the stalk of F at x will be a module over the local ring (stalk) Rx, for every x∈X.
A morphism between two such OX-modules is a morphism of sheaves which is compatible with the given module structures. The category of OX-modules over a fixed locally ringed space (X, OX) is an abelian category
.
An important subcategory of the category of OX-modules is the category of quasi-coherent sheaves on X. A sheaf of OX-modules is called quasi-coherent if it is, locally, isomorphic to the cokernel of a map between free OX-modules. A coherent sheaf
F is a quasi-coherent sheaf which is, locally, of finite type and for every open subset U of X the kernel of any morphism from a free OU-modules of finite rank to FU is also of finite type.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a ringed space is, intuitively speaking, a space together with a collection of commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
s, the elements of which are "functions" on each open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
of the space. Ringed spaces appear throughout analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
and are also used to define the scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
s of algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
.
Definition
Formally, a ringed space (X, OX) is a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X together with a sheaf
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
of rings OX on X. The sheaf OX is called the structure sheaf of X.
A locally ringed space is a ringed space (X, OX) such that all stalks of OX are local ring
Local ring
In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...
s (i.e. they have unique maximal ideal
Maximal ideal
In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
s). Note that it is not required that OX(U) be a local ring for every open set U. In fact, that is almost never going to be the case.
Examples
An arbitrary topological space X can be considered a locally ringed space by taking OX to be the sheaf of real-valued (or complex-valued) continuous functionContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s on open subsets of X (there may exist continuous functions over open subsets of X which are not the restriction of any continuous function over X). The stalk
Stalk (sheaf)
The stalk of a sheaf is a mathematical construction capturing the behaviour of a sheaf around a given point.-Motivation and definition:Sheaves are defined on open sets, but the underlying topological space X consists of points. It is reasonable to attempt to isolate the behavior of a sheaf at a...
at a point x can be thought of as the set of all germ
Germ (mathematics)
In mathematics, the notion of a germ of an object in/on a topological space captures the local properties of the object. In particular, the objects in question are mostly functions and subsets...
s of continuous functions at x; this is a local ring with maximal ideal
Maximal ideal
In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
consisting of those germs whose value at x is 0.
If X is a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
with some extra structure, we can also take the sheaf of differentiable, or complex-analytic
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
functions. Both of these give rise to locally ringed spaces.
If X is an algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
carrying the Zariski topology
Zariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
, we can define a locally ringed space by taking OX(U) to be the ring of rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s defined on the Zariski-open set U which do not blow up (become infinite) within U. The important generalization of this example is that of the spectrum
Spectrum of a ring
In abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
of any commutative ring; these spectra are also locally ringed spaces. Schemes
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
are locally ringed spaces obtained by "gluing together" spectra of commutative rings.
Morphisms
A morphismMorphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
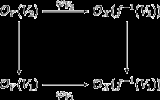
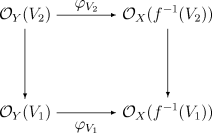
of ringed spaces is a continuous map between their underlying topological spaces together with (essentially) a morphism between their structure sheaves. Explicitly, a morphism from (X, OX) to (Y, OY) is given by the following data:
- a continuous map f : X → Y
- a family of ring homomorphismRing homomorphismIn ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
s φV : OY(V) → OX(f -1(V)) for every open setOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
V of Y which commute with the restriction maps. That is, if V1 ⊂ V2 are two open subsets of Y, then the following diagram must commuteCommutative diagramIn mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
(the vertical maps are the restriction homomorphisms):

There is an additional requirement for morphisms between locally ringed spaces:
- the ring homomorphisms induced by φ between the stalks of Y and the stalks of X must be local homomorphisms, i.e. for every x ∈ X the maximal ideal of the local ring (stalk) at f(x) ∈ Y is mapped to the maximal ideal of the local ring at x ∈ X.
Two morphisms can be composed to form a new morphism, and we obtain the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
of ringed spaces and the category of locally ringed spaces. Isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
s in these categories are defined as usual.
Tangent spaces
Locally ringed spaces have just enough structure to allow the meaningful definition of tangent spaceTangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
s. Let X be locally ringed space with structure sheaf OX; we want to define the tangent space Tx at the point x ∈ X. Take the local ring (stalk) Rx at the point x, with maximal ideal mx. Then kx := Rx/mx is a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
and mx/mx2 is a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over that field (the cotangent space
Cotangent space
In differential geometry, one can attach to every point x of a smooth manifold a vector space called the cotangent space at x. Typically, the cotangent space is defined as the dual space of the tangent space at x, although there are more direct definitions...
). The tangent space Tx is defined as the dual
Dual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of this vector space.
The idea is the following: a tangent vector at x should tell you how to "differentiate" "functions" at x, i.e. the elements of Rx. Now it is enough to know how to differentiate functions whose value at x is zero, since all other functions differ from these only by a constant, and we know how to differentiate constants. So we only need to worry about mx. Furthermore, if two functions are given with value zero at x, then their product has derivative 0 at x, by the product rule
Product rule
In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
. So we only need to know how to assign "numbers" to the elements of mx/mx2, and this is what the dual space does.
OX modules
Given a locally ringed space (X, OX), certain sheavesSheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
of modules on X occur in the applications, the OX-modules. To define them, consider a sheaf F of abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s on X. If F(U) is a module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over the ring OX(U) for every open set U in X, and the restriction maps are compatible with the module structure, then we call F an OX-module. In this case, the stalk of F at x will be a module over the local ring (stalk) Rx, for every x∈X.
A morphism between two such OX-modules is a morphism of sheaves which is compatible with the given module structures. The category of OX-modules over a fixed locally ringed space (X, OX) is an abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
.
An important subcategory of the category of OX-modules is the category of quasi-coherent sheaves on X. A sheaf of OX-modules is called quasi-coherent if it is, locally, isomorphic to the cokernel of a map between free OX-modules. A coherent sheaf
Coherent sheaf
In mathematics, especially in algebraic geometry and the theory of complex manifolds, coherent sheaves are a specific class of sheaves having particularly manageable properties closely linked to the geometrical properties of the underlying space. The definition of coherent sheaves is made with...
F is a quasi-coherent sheaf which is, locally, of finite type and for every open subset U of X the kernel of any morphism from a free OU-modules of finite rank to FU is also of finite type.

