
Isomorphism theorem
Encyclopedia
In mathematics
, specifically abstract algebra
, the isomorphism theorems are three theorem
s that describe the relationship between quotient
s, homomorphism
s, and subobject
s. Versions of the theorems exist for groups
, rings
, vector space
s, modules
, Lie algebra
s, and various other algebraic structure
s. In universal algebra
, the isomorphism theorems can be generalized to the context of algebras and congruences.
in her paper Abstrakter Aufbau der Idealtheorie in algebraischen Zahl- und Funktionenkörpern which was published in 1927 in Mathematische Annalen
. Less general versions of these theorems can be found in work of Richard Dedekind
and previous papers by Noether.
Three years later, B.L. van der Waerden
published his influential Algebra, the first abstract algebra
textbook that took the now-traditional groups
-rings
-fields
approach to the subject. Van der Waerden credited lectures by Noether on group theory
and Emil Artin
on algebra, as well as a seminar conducted by Artin, Wilhelm Blaschke
, Otto Schreier
, and van der Waerden himself on ideals
as the main references. The three isomorphism theorems, called homomorphism theorem, and two laws of isomorphism when applied to groups, appear explicitly.
. Note that some sources switch the numbering of the second and third theorems. Sometimes, the lattice theorem
is referred to as the fourth isomorphism theorem or the correspondence theorem.
. Then:
In particular, if φ is surjective
then H is isomorphic to G / ker(φ).
Technically, it is not necessary for N to be a normal subgroup, as long as S is a subgroup of the normalizer of N. In this case, the intersection S ∩ N is not a normal subgroup of G, but it is still a normal subgroup of S.
Then
The first isomorphism theorem follows from the category theoretical
fact that the category of groups
is (normal epi, mono)-factorizable; in other words, the normal epimorphisms
and the monomorphism
s form a factorization system
for the category. This is captured in the commutative diagram
in the margin, which shows the objects and morphisms whose existence can be deduced from the morphism f: G→H. The diagram shows that every morphism in the category of groups has a kernel
in the category theoretical sense; the arbitrary morphism f factors into , where ι is a monomorphism and π is an epimorphism (in a conormal category, all epimorphisms are normal). This is represented in the diagram by an object
, where ι is a monomorphism and π is an epimorphism (in a conormal category, all epimorphisms are normal). This is represented in the diagram by an object  and a monomorphism
and a monomorphism  (kernels are always monomorphisms), which complete the short exact sequence
(kernels are always monomorphisms), which complete the short exact sequence
running from the lower left to the upper right of the diagram. The use of the exact sequence convention saves us from having to draw the zero morphism
s from to H and
to H and 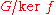 .
.
If the sequence is right split (i. e., there is a morphism σ that maps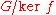 to a π-preimage of itself), then G is the semidirect product
to a π-preimage of itself), then G is the semidirect product
of the normal subgroup and the subgroup
and the subgroup  . If it is left split (i. e., there exists some
. If it is left split (i. e., there exists some 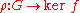 such that
such that 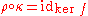 ), then it must also be right split, and
), then it must also be right split, and  is a direct product
is a direct product
decomposition of G. In general, the existence of a right split does not imply the existence of a left split; but in an abelian category
(such as the abelian groups), left splits and right splits are equivalent by the splitting lemma
, and a right split is sufficient to produce a direct sum decomposition . In an abelian category, all monomorphisms are also normal, and the diagram may be extended by a second short exact sequence
. In an abelian category, all monomorphisms are also normal, and the diagram may be extended by a second short exact sequence 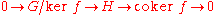 .
.
In the second isomorphism theorem, the product SN is the join of S and N in the lattice of subgroups
of G, while the intersection S ∩ N is the meet
.
The third isomorphism theorem is generalized by the nine lemma
to abelian categories and more general maps between objects. It is sometimes informally called the "freshman theorem", because "even a freshman could figure it out: just cancel out the Ks!"
are similar, with the notion of a normal subgroup replaced by the notion of an ideal
.
. Then:
In particular, if φ is surjective
then S is isomorphic to R / ker(φ).
Then
are particularly simple, since it is possible to form a quotient module
from any submodule. The isomorphism theorems for vector space
s and abelian group
s are special cases of these. For vector spaces, all of these theorems follow from the rank-nullity theorem
.
For all of the following theorems, the word “module” will mean “R-module”, where R is some fixed ring.
In particular, if φ is surjective then N is isomorphic to M / ker(φ).
Then
s.
Briefly, if is an algebra
is an algebra
, a congruence on is an equivalence relation
is an equivalence relation  on
on  which is a subalgebra when considered as a subset of
which is a subalgebra when considered as a subset of 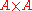 (the latter with the coordinate-wise operation structure). One can make the set of equivalence classes
(the latter with the coordinate-wise operation structure). One can make the set of equivalence classes 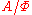 into an algebra of the same type by defining the operations via representatives; this will be well-defined since
into an algebra of the same type by defining the operations via representatives; this will be well-defined since 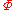 is a subalgebra of
is a subalgebra of 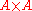 .
.
 and
and  are algebras, and
are algebras, and  is a homomorphism
is a homomorphism
 , then the equivalence relation
, then the equivalence relation 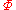 on
on  defined by
defined by  if and only if
if and only if
 is a congruence on
is a congruence on  , and the algebra
, and the algebra 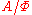 is isomorphic to the image of
is isomorphic to the image of  , which is a subalgebra of
, which is a subalgebra of  .
.
 , a subalgebra
, a subalgebra  of
of  , and a congruence
, and a congruence 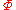 on
on  , we let
, we let  be the subset of
be the subset of  determined by all congruence classes that contain an element of
determined by all congruence classes that contain an element of  , and we let
, and we let 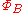 be the intersection of
be the intersection of 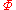 (considered as a subset of
(considered as a subset of 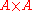 ) with
) with 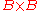 . Then
. Then  is a subalgebra of
is a subalgebra of 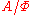 ,
, 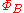 is a congruence on
is a congruence on  , and the algebra
, and the algebra  is isomorphic to the algebra
is isomorphic to the algebra  .
.
 be an algebra, and let
be an algebra, and let  and
and 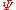 be two congruence relations on
be two congruence relations on  , with
, with 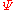 contained in
contained in 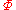 . Then
. Then 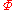 determines a congruence
determines a congruence  on
on 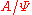 defined by
defined by  if and only if
if and only if  and
and  are equivalent modulo
are equivalent modulo 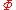 (where
(where  represents the
represents the 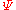 -equivalence class of
-equivalence class of  ), and
), and  is isomorphic to
is isomorphic to  .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, the isomorphism theorems are three theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
s that describe the relationship between quotient
Quotient
In mathematics, a quotient is the result of division. For example, when dividing 6 by 3, the quotient is 2, while 6 is called the dividend, and 3 the divisor. The quotient further is expressed as the number of times the divisor divides into the dividend e.g. The quotient of 6 and 2 is also 3.A...
s, homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
s, and subobject
Subobject
In category theory, a branch of mathematics, a subobject is, roughly speaking, an object which sits inside another object in the same category. The notion is a generalization of the older concepts of subset from set theory and subgroup from group theory...
s. Versions of the theorems exist for groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
, vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s, modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
, Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s, and various other algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
s. In universal algebra
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
, the isomorphism theorems can be generalized to the context of algebras and congruences.
History
The isomorphism theorems were formulated in some generality for homomorphisms of modules by Emmy NoetherEmmy Noether
Amalie Emmy Noether was an influential German mathematician known for her groundbreaking contributions to abstract algebra and theoretical physics. Described by David Hilbert, Albert Einstein and others as the most important woman in the history of mathematics, she revolutionized the theories of...
in her paper Abstrakter Aufbau der Idealtheorie in algebraischen Zahl- und Funktionenkörpern which was published in 1927 in Mathematische Annalen
Mathematische Annalen
Mathematische Annalen is a German mathematical research journal founded in 1868 by Alfred Clebsch and Carl Neumann...
. Less general versions of these theorems can be found in work of Richard Dedekind
Richard Dedekind
Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...
and previous papers by Noether.
Three years later, B.L. van der Waerden
Bartel Leendert van der Waerden
Bartel Leendert van der Waerden was a Dutch mathematician and historian of mathematics....
published his influential Algebra, the first abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
textbook that took the now-traditional groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
-rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
-fields
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
approach to the subject. Van der Waerden credited lectures by Noether on group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
and Emil Artin
Emil Artin
Emil Artin was an Austrian-American mathematician of Armenian descent.-Parents:Emil Artin was born in Vienna to parents Emma Maria, née Laura , a soubrette on the operetta stages of Austria and Germany, and Emil Hadochadus Maria Artin, Austrian-born of Armenian descent...
on algebra, as well as a seminar conducted by Artin, Wilhelm Blaschke
Wilhelm Blaschke
Wilhelm Johann Eugen Blaschke was an Austro-Hungarian differential and integral geometer.His students included Shiing-Shen Chern, Luis Santaló, and Emanuel Sperner....
, Otto Schreier
Otto Schreier
Otto Schreier was an Austrian mathematician who made major contributions in combinatorial group theory and in the topology of Lie groups. He studied mathematics at the University of Vienna and obtained his doctorate in 1923, under the supervision of Philipp Furtwängler...
, and van der Waerden himself on ideals
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
as the main references. The three isomorphism theorems, called homomorphism theorem, and two laws of isomorphism when applied to groups, appear explicitly.
Groups
We first state the three isomorphism theorems in the context of groupsGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. Note that some sources switch the numbering of the second and third theorems. Sometimes, the lattice theorem
Lattice theorem
In mathematics, the lattice theorem, sometimes referred to as the fourth isomorphism theorem or the correspondence theorem, states that if N is a normal subgroup of a group G, then there exists a bijection from the set of all subgroups A of G such that A contains N, onto the set of all subgroups...
is referred to as the fourth isomorphism theorem or the correspondence theorem.
First isomorphism theorem
Let G and H be groups, and let φ: G → H be a homomorphismGroup homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
. Then:
- The kernelKernel (algebra)In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
of φ is a normal subgroupNormal subgroupIn abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
of G, - The imageImage (mathematics)In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of φ is a subgroupSubgroupIn group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of H, and - The image of φ is isomorphicGroup isomorphismIn abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
to the quotient groupQuotient groupIn mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
G / ker(φ).
In particular, if φ is surjective
Surjective function
In mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
then H is isomorphic to G / ker(φ).
Second isomorphism theorem
Let G be a group. Let S be a subgroup of G, and let N be a normal subgroup of G. Then:- The product SN is a subgroup of G,
- The intersectionIntersection (set theory)In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
S ∩ N is a normal subgroup of S, and - The quotient groups (SN) / N and S / (S ∩ N) are isomorphic.
Technically, it is not necessary for N to be a normal subgroup, as long as S is a subgroup of the normalizer of N. In this case, the intersection S ∩ N is not a normal subgroup of G, but it is still a normal subgroup of S.
Third isomorphism theorem
Let G be a group. Let N and K be normal subgroups of G, with- K ⊆ N ⊆ G.
Then
- The quotient N / K is a normal subgroup of the quotient G / K, and
- The quotient group (G / K) / (N / K) is isomorphic to G / N.
Discussion
 |
The first isomorphism theorem follows from the category theoretical
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
fact that the category of groups
Category of groups
In mathematics, the category Grp has the class of all groups for objects and group homomorphisms for morphisms. As such, it is a concrete category...
is (normal epi, mono)-factorizable; in other words, the normal epimorphisms
Normal morphism
In category theory and its applications to mathematics, a normal monomorphism or conormal epimorphism is a particularly well-behaved type of morphism.A normal category is a category in which every monomorphism is normal...
and the monomorphism
Monomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
s form a factorization system
Factorization system
In mathematics, it can be shown that every function can be written as the composite of a surjective function followed by an injective function. Factorization systems are a generalization of this situation in category theory.-Definition:...
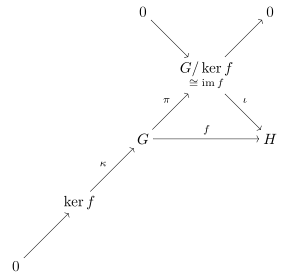
for the category. This is captured in the commutative diagram
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
in the margin, which shows the objects and morphisms whose existence can be deduced from the morphism f: G→H. The diagram shows that every morphism in the category of groups has a kernel
Kernel (category theory)
In category theory and its applications to other branches of mathematics, kernels are a generalization of the kernels of group homomorphisms, the kernels of module homomorphisms and certain other kernels from algebra...
in the category theoretical sense; the arbitrary morphism f factors into
 , where ι is a monomorphism and π is an epimorphism (in a conormal category, all epimorphisms are normal). This is represented in the diagram by an object
, where ι is a monomorphism and π is an epimorphism (in a conormal category, all epimorphisms are normal). This is represented in the diagram by an object  and a monomorphism
and a monomorphism  (kernels are always monomorphisms), which complete the short exact sequence
(kernels are always monomorphisms), which complete the short exact sequenceExact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
running from the lower left to the upper right of the diagram. The use of the exact sequence convention saves us from having to draw the zero morphism
Zero morphism
In category theory, a zero morphism is a special kind of morphism exhibiting properties like those to and from a zero object.Suppose C is a category, and f : X → Y is a morphism in C...
s from
 to H and
to H and 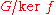 .
.If the sequence is right split (i. e., there is a morphism σ that maps
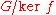 to a π-preimage of itself), then G is the semidirect product
to a π-preimage of itself), then G is the semidirect productSemidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of the normal subgroup
 and the subgroup
and the subgroup  . If it is left split (i. e., there exists some
. If it is left split (i. e., there exists some 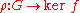 such that
such that 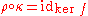 ), then it must also be right split, and
), then it must also be right split, and  is a direct product
is a direct productDirect product
In mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
decomposition of G. In general, the existence of a right split does not imply the existence of a left split; but in an abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
(such as the abelian groups), left splits and right splits are equivalent by the splitting lemma
Splitting lemma
In mathematics, and more specifically in homological algebra, the splitting lemma states that in any abelian category, the following statements for short exact sequence are equivalent....
, and a right split is sufficient to produce a direct sum decomposition
 . In an abelian category, all monomorphisms are also normal, and the diagram may be extended by a second short exact sequence
. In an abelian category, all monomorphisms are also normal, and the diagram may be extended by a second short exact sequence 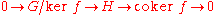 .
.In the second isomorphism theorem, the product SN is the join of S and N in the lattice of subgroups
Lattice of subgroups
In mathematics, the lattice of subgroups of a group G is the lattice whose elements are the subgroups of G, with the partial order relation being set inclusion....
of G, while the intersection S ∩ N is the meet
Meet (mathematics)
In mathematics, join and meet are dual binary operations on the elements of a partially ordered set. A join on a set is defined as the supremum with respect to a partial order on the set, provided a supremum exists...
.
The third isomorphism theorem is generalized by the nine lemma
Nine lemma
In mathematics, the nine lemma is a statement about commutative diagrams and exact sequences valid in any abelian category, as well as in the category of groups. It states: ifis a commutative diagram and all columns as well as the two bottom rows are exact, then the top row is exact as well...
to abelian categories and more general maps between objects. It is sometimes informally called the "freshman theorem", because "even a freshman could figure it out: just cancel out the Ks!"
Rings
The statements of the theorems for ringsRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
are similar, with the notion of a normal subgroup replaced by the notion of an ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
.
First isomorphism theorem
Let R and S be rings, and let φ: R → S be a ring homomorphismRing homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
. Then:
- The kernelKernel (algebra)In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
of φ is an ideal of R, - The imageImage (mathematics)In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of φ is a subringSubringIn mathematics, a subring of R is a subset of a ring, is itself a ring with the restrictions of the binary operations of addition and multiplication of R, and which contains the multiplicative identity of R...
of S, and - The image of φ is isomorphic to the quotient ringQuotient ringIn ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
R / ker(φ).
In particular, if φ is surjective
Surjective function
In mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
then S is isomorphic to R / ker(φ).
Second isomorphism theorem
Let R be a ring. Let S be a subring of R, and let I be an ideal of R. Then:- The sum S + I = {s + i | s ∈ S, i ∈ I} is a subring of R,
- The intersection S ∩ I is an ideal of S, and
- The quotient rings (S + I) / I and S / (S ∩ I) are isomorphic.
Third isomorphism theorem
Let R be a ring. Let A and B be ideals of R, with- B ⊆ A ⊆ R.
Then
- The set A / B is an ideal of the quotient R / B, and
- The quotient ring (R / B) / (A / B) is isomorphic to R / A.
Modules
The statements of the isomorphism theorems for modulesModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
are particularly simple, since it is possible to form a quotient module
Quotient module
In abstract algebra, given a module and a submodule, one can construct their quotient module. This construction, described below, is analogous to how one obtains the ring of integers modulo an integer n, see modular arithmetic...
from any submodule. The isomorphism theorems for vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s and abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s are special cases of these. For vector spaces, all of these theorems follow from the rank-nullity theorem
Rank-nullity theorem
In mathematics, the rank–nullity theorem of linear algebra, in its simplest form, states that the rank and the nullity of a matrix add up to the number of columns of the matrix. Specifically, if A is an m-by-n matrix over some field, thenThis applies to linear maps as well...
.
For all of the following theorems, the word “module” will mean “R-module”, where R is some fixed ring.
First isomorphism theorem
Let M and N be modules, and let φ: M → N be a homomorphism. Then:- The kernelKernel (algebra)In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
of φ is a submodule of M, - The imageImage (mathematics)In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of φ is a submodule of N, and - The image of φ is isomorphic to the quotient moduleQuotient moduleIn abstract algebra, given a module and a submodule, one can construct their quotient module. This construction, described below, is analogous to how one obtains the ring of integers modulo an integer n, see modular arithmetic...
M / ker(φ).
In particular, if φ is surjective then N is isomorphic to M / ker(φ).
Second isomorphism theorem
Let M be a module, and let S and T be submodules of M. Then:- The sum S + T = {s + t | s ∈ S, t ∈ T} is a submodule of M,
- The intersection S ∩ T is a submodule of S, and
- The quotient modules (S + T) / T and S / (S ∩ T) are isomorphic.
Third isomorphism theorem
Let M be a module. Let S and T be submodules of M, with- T ⊆ S ⊆ M.
Then
- The quotient S / T is a submodule of the quotient M / T, and
- The quotient (M / T) / (S / T) is isomorphic to M / S.
General
To generalise this to universal algebra, normal subgroups need to be replaced by congruenceCongruence relation
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure...
s.
Briefly, if
 is an algebra
is an algebraUniversal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
, a congruence on
 is an equivalence relation
is an equivalence relation  on
on  which is a subalgebra when considered as a subset of
which is a subalgebra when considered as a subset of  (the latter with the coordinate-wise operation structure). One can make the set of equivalence classes
(the latter with the coordinate-wise operation structure). One can make the set of equivalence classes 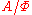 into an algebra of the same type by defining the operations via representatives; this will be well-defined since
into an algebra of the same type by defining the operations via representatives; this will be well-defined since 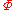 is a subalgebra of
is a subalgebra of 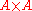 .
.First Isomorphism Theorem
If and
and  are algebras, and
are algebras, and  is a homomorphism
is a homomorphismHomomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
 , then the equivalence relation
, then the equivalence relation 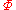 on
on  defined by
defined by  if and only if
if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
 is a congruence on
is a congruence on  , and the algebra
, and the algebra 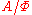 is isomorphic to the image of
is isomorphic to the image of  , which is a subalgebra of
, which is a subalgebra of  .
.Second Isomorphism Theorem
Given an algebra , a subalgebra
, a subalgebra  of
of  , and a congruence
, and a congruence 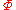 on
on  , we let
, we let  be the subset of
be the subset of  determined by all congruence classes that contain an element of
determined by all congruence classes that contain an element of  , and we let
, and we let 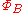 be the intersection of
be the intersection of 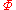 (considered as a subset of
(considered as a subset of 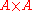 ) with
) with 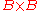 . Then
. Then  is a subalgebra of
is a subalgebra of 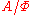 ,
, 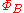 is a congruence on
is a congruence on  , and the algebra
, and the algebra  is isomorphic to the algebra
is isomorphic to the algebra  .
.Third Isomorphism Theorem
Let be an algebra, and let
be an algebra, and let  and
and 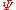 be two congruence relations on
be two congruence relations on  , with
, with 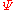 contained in
contained in 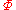 . Then
. Then 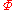 determines a congruence
determines a congruence  on
on 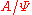 defined by
defined by  if and only if
if and only if  and
and  are equivalent modulo
are equivalent modulo 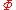 (where
(where  represents the
represents the 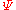 -equivalence class of
-equivalence class of  ), and
), and  is isomorphic to
is isomorphic to  .
.See also
- Butterfly lemma, sometimes called the fourth isomorphism theorem
- Lattice theoremLattice theoremIn mathematics, the lattice theorem, sometimes referred to as the fourth isomorphism theorem or the correspondence theorem, states that if N is a normal subgroup of a group G, then there exists a bijection from the set of all subgroups A of G such that A contains N, onto the set of all subgroups...
, sometimes called the fourth isomorphism theorem - Splitting lemmaSplitting lemmaIn mathematics, and more specifically in homological algebra, the splitting lemma states that in any abelian category, the following statements for short exact sequence are equivalent....
, which refines the first isomorphism theorem for split sequences

