Equipartition theorem - AbsoluteAstronomy.com

Classical physics

What "classical physics" refers to depends on the context. When discussing special relativity, it refers to the Newtonian physics which preceded relativity, i.e. the branches of physics based on principles developed before the rise of relativity and quantum mechanics...

statistical mechanics

Statistical mechanics

Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...

, the equipartition theorem is a general formula that relates the temperature

Temperature

Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...

of a system with its average energies

Energy

In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...

. The equipartition theorem is also known as the law of equipartition, equipartition of energy, or simply equipartition. The original idea of equipartition was that, in thermal equilibrium

Thermal equilibrium

Thermal equilibrium is a theoretical physical concept, used especially in theoretical texts, that means that all temperatures of interest are unchanging in time and uniform in space...

, energy is shared equally among all of its various forms; for example, the average kinetic energy

Kinetic energy

The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...

per degree of freedom

Degrees of freedom (physics and chemistry)

A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...

in the translational motion

Translation (physics)

In physics, translation is movement that changes the position of an object, as opposed to rotation. For example, according to Whittaker:...

of a molecule should equal that of its rotational motions.

The equipartition theorem makes quantitative predictions. Like the virial theorem, it gives the total average kinetic and potential energies for a system at a given temperature, from which the system's heat capacity

Heat capacity

Heat capacity , or thermal capacity, is the measurable physical quantity that characterizes the amount of heat required to change a substance's temperature by a given amount...

can be computed. However, equipartition also gives the average values of individual components of the energy, such as the kinetic energy of a particular particle or the potential energy of a single spring

Spring (device)

A spring is an elastic object used to store mechanical energy. Springs are usually made out of spring steel. Small springs can be wound from pre-hardened stock, while larger ones are made from annealed steel and hardened after fabrication...

. For example, it predicts that every molecule in a monoatomic ideal gas

Ideal gas

An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...

has an average kinetic energy of (3/2)k_BT in thermal equilibrium, where k_B is the Boltzmann constant and T is the (thermodynamic) temperature

Thermodynamic temperature

Thermodynamic temperature is the absolute measure of temperature and is one of the principal parameters of thermodynamics. Thermodynamic temperature is an "absolute" scale because it is the measure of the fundamental property underlying temperature: its null or zero point, absolute zero, is the...

. More generally, it can be applied to any classical system

Classical physics

in thermal equilibrium

Thermal equilibrium

Thermal equilibrium is a theoretical physical concept, used especially in theoretical texts, that means that all temperatures of interest are unchanging in time and uniform in space...

, no matter how complicated. The equipartition theorem can be used to derive the ideal gas law

Ideal gas law

The ideal gas law is the equation of state of a hypothetical ideal gas. It is a good approximation to the behavior of many gases under many conditions, although it has several limitations. It was first stated by Émile Clapeyron in 1834 as a combination of Boyle's law and Charles's law...

, and the Dulong–Petit law

Dulong–Petit law

The Dulong–Petit law, a chemical law proposed in 1819 by French physicists Pierre Louis Dulong and Alexis Thérèse Petit, states the classical expression for the molar specific heat capacity of a crystal...

for the specific heat capacities of solids. It can also be used to predict the properties of star

Star

A star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...

s, even white dwarf

White dwarf

A white dwarf, also called a degenerate dwarf, is a small star composed mostly of electron-degenerate matter. They are very dense; a white dwarf's mass is comparable to that of the Sun and its volume is comparable to that of the Earth. Its faint luminosity comes from the emission of stored...

s and neutron star

Neutron star

A neutron star is a type of stellar remnant that can result from the gravitational collapse of a massive star during a Type II, Type Ib or Type Ic supernova event. Such stars are composed almost entirely of neutrons, which are subatomic particles without electrical charge and with a slightly larger...

s, since it holds even when relativistic

Special relativity

Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...

effects are considered.

Although the equipartition theorem makes very accurate predictions in certain conditions, it becomes inaccurate when quantum effects are significant, such as at low temperatures. When the thermal energy

Thermal energy

Thermal energy is the part of the total internal energy of a thermodynamic system or sample of matter that results in the system's temperature....

k_BT is smaller than the quantum energy spacing in a particular degree of freedom

Degrees of freedom (physics and chemistry)

A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...

, the average energy and heat capacity of this degree of freedom are less than the values predicted by equipartition. Such a degree of freedom is said to be "frozen out" when the thermal energy is much smaller than this spacing. For example, the heat capacity of a solid decreases at low temperatures as various types of motion become frozen out, rather than remaining constant as predicted by equipartition. Such decreases in heat capacity were among the first sign to physicists of the 19th century that classical physics was incorrect and that a new, more subtle, scientific model was required. Along with other evidence, equipartition's failure to model black-body radiation—also known as the ultraviolet catastrophe

Ultraviolet catastrophe

The ultraviolet catastrophe, also called the Rayleigh–Jeans catastrophe, was a prediction of late 19th century/early 20th century classical physics that an ideal black body at thermal equilibrium will emit radiation with infinite power....

—led Max Planck

Max Planck

Max Karl Ernst Ludwig Planck, ForMemRS, was a German physicist who actualized the quantum physics, initiating a revolution in natural science and philosophy. He is regarded as the founder of the quantum theory, for which he received the Nobel Prize in Physics in 1918.-Life and career:Planck came...

to suggest that energy in the oscillators in an object, which emit light, were quantized, a revolutionary hypothesis that spurred the development of quantum mechanics

Quantum mechanics

Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...

and quantum field theory

Quantum field theory

Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...

Basic concept and simple examples

The name "equipartition" means "equal division," as derived from the Latin

Latin

Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...

equi from the antecedent, æquus ("equal or even"), and partition from the antecedent, partitionem ("division, portion"). The original concept of equipartition was that the total kinetic energy

Kinetic energy

of a system is shared equally among all of its independent parts, on the average, once the system has reached thermal equilibrium. Equipartition also makes quantitative predictions for these energies. For example, it predicts that every atom of a noble gas

Noble gas

The noble gases are a group of chemical elements with very similar properties: under standard conditions, they are all odorless, colorless, monatomic gases, with very low chemical reactivity...

, in thermal equilibrium at temperature T, has an average translational kinetic energy of (3/2)k_BT, where k_B is the Boltzmann constant. As a consequence, since kinetic energy is equal to 1/2*mass*velocity^2, the heavier atoms of xenon

Xenon

Xenon is a chemical element with the symbol Xe and atomic number 54. The element name is pronounced or . A colorless, heavy, odorless noble gas, xenon occurs in the Earth's atmosphere in trace amounts...

have a lower average speed than do the lighter atoms of helium

Helium

Helium is the chemical element with atomic number 2 and an atomic weight of 4.002602, which is represented by the symbol He. It is a colorless, odorless, tasteless, non-toxic, inert, monatomic gas that heads the noble gas group in the periodic table...

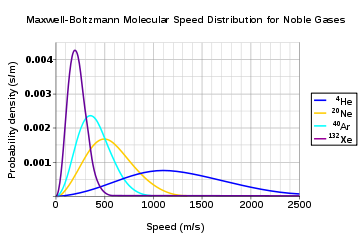
at the same temperature. Figure 2 shows the Maxwell–Boltzmann distribution for the speeds of the atoms in four noble gases.

In this example, the key point is that the kinetic energy is quadratic in the velocity. The equipartition theorem shows that in thermal equilibrium, any degree of freedom

Degrees of freedom (physics and chemistry)

A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...

(such as a component of the position or velocity of a particle) which appears only quadratically in the energy has an average energy of k_BT and therefore contributes k_B to the system's heat capacity

Heat capacity

Heat capacity , or thermal capacity, is the measurable physical quantity that characterizes the amount of heat required to change a substance's temperature by a given amount...

. This has many applications.

Translational energy and ideal gases

The (Newtonian) kinetic energy of a particle of mass m, velocity v is given by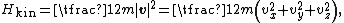

where v_x, v_y and v_z are the Cartesian components of the velocity v. Here, H is short for Hamiltonian

Hamiltonian (quantum mechanics)

In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...

, and used henceforth as a symbol for energy because the Hamiltonian formalism

Hamiltonian mechanics

Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...

plays a central role in the most general form of the equipartition theorem.

Since the kinetic energy is quadratic in the components of the velocity, by equipartition these three components each contribute k_BT to the average kinetic energy in thermal equilibrium. Thus the average kinetic energy of the particle is (3/2)k_BT, as in the example of noble gases above.

More generally, in an ideal gas, the total energy consists purely of (translational) kinetic energy: by assumption, the particles have no internal degrees of freedom and move independently of one another. Equipartition therefore predicts that the average total energy of an ideal gas of N particles is (3/2) N k_B T.

It follows that the heat capacity

Heat capacity

Heat capacity , or thermal capacity, is the measurable physical quantity that characterizes the amount of heat required to change a substance's temperature by a given amount...

of the gas is (3/2) N k_B and hence, in particular, the heat capacity of a mole

Mole (unit)

The mole is a unit of measurement used in chemistry to express amounts of a chemical substance, defined as an amount of a substance that contains as many elementary entities as there are atoms in 12 grams of pure carbon-12 , the isotope of carbon with atomic weight 12. This corresponds to a value...

of such gas particles is (3/2)N_Ak_B = (3/2)R, where N_A is the Avogadro constant and R is the gas constant

Gas constant

The gas constant is a physical constant which is featured in many fundamental equations in the physical sciences, such as the ideal gas law and the Nernst equation. It is equivalent to the Boltzmann constant, but expressed in units of energy The gas constant (also known as the molar, universal,...

. Since R ≈ 2 cal

Calorie

The calorie is a pre-SI metric unit of energy. It was first defined by Nicolas Clément in 1824 as a unit of heat, entering French and English dictionaries between 1841 and 1867. In most fields its use is archaic, having been replaced by the SI unit of energy, the joule...

/(mol

Mole (unit)

·K

Kelvin

The kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...

), equipartition predicts that the molar heat capacity of an ideal gas is roughly 3 cal/(mol·K). This prediction is confirmed by experiment.

The mean kinetic energy also allows the root mean square speed

Root mean square speed

Root-mean-square speed is the measure of the speed of particles in a gas that is most convenient for problem solving within the kinetic theory of gases. It is defined as the square root of the average velocity-squared of the molecules in a gas...

v_rms of the gas particles to be calculated:

where M = N_Am is the mass of a mole of gas particles. This result is useful for many applications such as Graham's law

Graham's law

Graham's law, known as Graham's law of effusion, was formulated by Scottish physical chemist Thomas Graham in 1846. Graham found experimentally that the rate of effusion of a gas is inversely proportional to the square root of the mass of its particles...

of effusion

Effusion

In physics, effusion is the process in which individual molecules flow through a hole without collisions between molecules. This occurs if the diameter of the hole is considerably smaller than the mean free path of the molecules...

, which provides a method for enriching

Enriched uranium

Enriched uranium is a kind of uranium in which the percent composition of uranium-235 has been increased through the process of isotope separation. Natural uranium is 99.284% 238U isotope, with 235U only constituting about 0.711% of its weight...

uranium

Uranium

Uranium is a silvery-white metallic chemical element in the actinide series of the periodic table, with atomic number 92. It is assigned the chemical symbol U. A uranium atom has 92 protons and 92 electrons, of which 6 are valence electrons...

Rotational energy and molecular tumbling in solution

A similar example is provided by a rotating molecule with principal moments of inertia I₁, I₂ and I₃. The rotational energy of such a molecule is given by

where ω₁, ω₂, and ω₃ are the principal components of the angular velocity

Angular velocity

In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...

. By exactly the same reasoning as in the translational case, equipartition implies that in thermal equilibrium the average rotational energy of each particle is (3/2)k_BT. Similarly, the equipartition theorem allows the average (more precisely, the root mean square) angular speed of the molecules to be calculated.

The tumbling of rigid molecules—that is, the random rotations of molecules in solution—plays a key role in the relaxation

Relaxation (NMR)

In nuclear magnetic resonance spectroscopy and magnetic resonance imaging the term relaxation describes several processes by which nuclear magnetization prepared in a non-equilibrium state return to the equilibrium distribution. In other words, relaxation describes how fast spins "forget" the...

s observed by nuclear magnetic resonance

Nuclear magnetic resonance

Nuclear magnetic resonance is a physical phenomenon in which magnetic nuclei in a magnetic field absorb and re-emit electromagnetic radiation...

, particularly protein NMR

Protein nuclear magnetic resonance spectroscopy

Nuclear magnetic resonance spectroscopy of proteins is a field of structural biology in which NMR spectroscopy is used to obtain information about the structure and dynamics of proteins. The field was pioneered by Richard R. Ernst and Kurt Wüthrich, among others...

and residual dipolar coupling

Residual dipolar coupling

The residual dipolar coupling between two spins in a molecule occurs if the molecules in solution exhibit a partial alignment leading to an incomplete averaging of spatially anisotropic dipolar couplings....

s. Rotational diffusion can also be observed by other biophysical probes such as fluorescence anisotropy

Fluorescence anisotropy

Fluorescence anisotropy is the phenomenon where the light emitted by a fluorophore has unequal intensities along different axes of polarization...

, flow birefringence

Flow birefringence

In biochemistry, flow birefringence is a hydrodynamic technique for measuring the rotational diffusion constants . The birefringence of a solution sandwiched between two concentric cylinders is measured as a function of the difference in rotational speed between the inner and outer cylinders...

and dielectric spectroscopy

Dielectric spectroscopy

Dielectric spectroscopy , and also known as electrochemical impedance spectroscopy, measures the dielectric properties of a medium as a function of frequency...

Potential energy and harmonic oscillators

Equipartition applies to potential energies

Potential energy

In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...

as well as kinetic energies: important examples include harmonic oscillator

Harmonic oscillator

In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....

s such as a spring

Spring (device)

, which has a quadratic potential energy

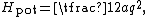
where the constant a describes the stiffness of the spring and q is the deviation from equilibrium. If such a one dimensional system has mass m, then its kinetic energy H_kin is

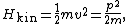
where v and p = mv denote the velocity and momentum of the oscillator. Combining these terms yields the total energy

Equipartition therefore implies that in thermal equilibrium, the oscillator has average energy

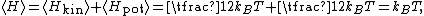
where the angular brackets

denote the average of the enclosed quantity,

This result is valid for any type of harmonic oscillator, such as a pendulum

Pendulum

A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced from its resting equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position...

, a vibrating molecule or a passive electronic oscillator

Electronic oscillator

An electronic oscillator is an electronic circuit that produces a repetitive electronic signal, often a sine wave or a square wave. They are widely used in innumerable electronic devices...

. Systems of such oscillators arise in many situations; by equipartition, each such oscillator receives an average total energy k_BT and hence contributes k_B to the system's heat capacity

Heat capacity

Heat capacity , or thermal capacity, is the measurable physical quantity that characterizes the amount of heat required to change a substance's temperature by a given amount...

. This can be used to derive the formula for Johnson–Nyquist noise

Johnson–Nyquist noise

Johnson–Nyquist noise is the electronic noise generated by the thermal agitation of the charge carriers inside an electrical conductor at equilibrium, which happens regardless of any applied voltage...

and the Dulong–Petit law

Dulong–Petit law

of solid heat capacities. The latter application was particularly significant in the history of equipartition.

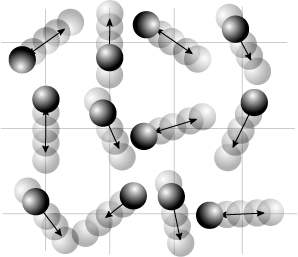
Specific heat capacity of solids

For more details on the molar specific heat capacities of solid
Solid
Solid is one of the three classical states of matter . It is characterized by structural rigidity and resistance to changes of shape or volume. Unlike a liquid, a solid object does not flow to take on the shape of its container, nor does it expand to fill the entire volume available to it like a...

s, see Einstein solid
Einstein solid
The Einstein solid is a model of a solid based on two assumptions:* Each atom in the lattice is an independent 3D quantum harmonic oscillator* All atoms oscillate with the same frequency...

and Debye model
Debye model
In thermodynamics and solid state physics, the Debye model is a method developed by Peter Debye in 1912 for estimating the phonon contribution to the specific heat in a solid. It treats the vibrations of the atomic lattice as phonons in a box, in contrast to the Einstein model, which treats the...

.

An important application of the equipartition theorem is to the specific heat capacity of a crystalline solid. Each atom in such a solid can oscillate in three independent directions, so the solid can be viewed as a system of 3N independent simple harmonic oscillators, where N denotes the number of atoms in the lattice. Since each harmonic oscillator has average energy k_BT, the average total energy of the solid is 3Nk_BT, and its heat capacity is 3Nk_B.

By taking N to be the Avogadro constant N_A, and using the relation R = N_Ak_B between the gas constant

Gas constant

R and the Boltzmann constant k_B, this provides an explanation for the Dulong–Petit law

Dulong–Petit law

of specific heat capacities of solids, which stated that the specific heat capacity (per unit mass) of a solid element is inversely proportional to its atomic weight

Atomic weight

Atomic weight is a dimensionless physical quantity, the ratio of the average mass of atoms of an element to 1/12 of the mass of an atom of carbon-12...

. A modern version is that the molar heat capacity of a solid is 3R ≈ 6 cal/(mol·K).

However, this law is inaccurate at lower temperatures, due to quantum effects; it is also inconsistent with the experimentally derived third law of thermodynamics

Third law of thermodynamics

The third law of thermodynamics is a statistical law of nature regarding entropy:For other materials, the residual entropy is not necessarily zero, although it is always zero for a perfect crystal in which there is only one possible ground state.-History:...

, according to which the molar heat capacity of any substance must go to zero as the temperature goes to absolute zero. A more accurate theory, incorporating quantum effects, was developed by Albert Einstein

Albert Einstein

Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...

(1907) and Peter Debye

Peter Debye

Peter Joseph William Debye FRS was a Dutch physicist and physical chemist, and Nobel laureate in Chemistry.-Early life:...

(1911).

Many other physical systems can be modeled as sets of coupled oscillators. The motions of such oscillators can be decomposed into normal mode

Normal mode

A normal mode of an oscillating system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The frequencies of the normal modes of a system are known as its natural frequencies or resonant frequencies...

s, like the vibrational modes of a piano string or the resonance

Resonance

In physics, resonance is the tendency of a system to oscillate at a greater amplitude at some frequencies than at others. These are known as the system's resonant frequencies...

s of an organ pipe

Organ pipe

An organ pipe is a sound-producing element of the pipe organ that resonates at a specific pitch when pressurized air is driven through it. Each pipe is tuned to a specific note of the musical scale...

. On the other hand, equipartition often breaks down for such systems, because there is no exchange of energy between the normal modes. In an extreme situation, the modes are independent and so their energies are independently conserved. This shows that some sort of mixing of energies, formally called ergodicity, is important for the law of equipartition to hold.

Sedimentation of particles

Potential energies are not always quadratic in the position. However, the equipartition theorem also shows that if a degree of freedom x contributes only a multiple of x^s (for a fixed real number s) to the energy, then in thermal equilibrium the average energy of that part is k_BT/s.

There is a simple application of this extension to the sedimentation

Sedimentation

Sedimentation is the tendency for particles in suspension to settle out of the fluid in which they are entrained, and come to rest against a barrier. This is due to their motion through the fluid in response to the forces acting on them: these forces can be due to gravity, centrifugal acceleration...

of particles under gravity

Gravitation

Gravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...

. For example, the haze sometimes seen in beer

Beer

Beer is the world's most widely consumed andprobably oldest alcoholic beverage; it is the third most popular drink overall, after water and tea. It is produced by the brewing and fermentation of sugars, mainly derived from malted cereal grains, most commonly malted barley and malted wheat...

can be caused by clumps of protein

Protein

Proteins are biochemical compounds consisting of one or more polypeptides typically folded into a globular or fibrous form, facilitating a biological function. A polypeptide is a single linear polymer chain of amino acids bonded together by peptide bonds between the carboxyl and amino groups of...

s that scatter

Rayleigh scattering

Rayleigh scattering, named after the British physicist Lord Rayleigh, is the elastic scattering of light or other electromagnetic radiation by particles much smaller than the wavelength of the light. The particles may be individual atoms or molecules. It can occur when light travels through...

light. Over time, these clumps settle downwards under the influence of gravity, causing more haze near the bottom of a bottle than near its top. However, in a process working in the opposite direction, the particles also diffuse

Diffusion

Molecular diffusion, often called simply diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size of the particles...

back up towards the top of the bottle. Once equilibrium has been reached, the equipartition theorem may be used to determine the average position of a particular clump of buoyant mass m_b. For an infinitely tall bottle of beer, the gravitational potential energy

Potential energy

In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...

is given by

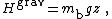
where z is the height of the protein clump in the bottle and g
Earth's gravity
The gravity of Earth, denoted g, refers to the acceleration that the Earth imparts to objects on or near its surface. In SI units this acceleration is measured in metres per second per second or equivalently in newtons per kilogram...

is the acceleration

Acceleration

In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...

due to gravity. Since s = 1, the average potential energy of a protein clump equals k_BT. Hence, a protein clump with a buoyant mass of 10 MDa (roughly the size of a virus

Virus

A virus is a small infectious agent that can replicate only inside the living cells of organisms. Viruses infect all types of organisms, from animals and plants to bacteria and archaea...

) would produce a haze with an average height of about 2 cm at equilibrium. The process of such sedimentation to equilibrium is described by the Mason–Weaver equation.

History

This article uses the non-SI
International System of Units
The International System of Units is the modern form of the metric system and is generally a system of units of measurement devised around seven base units and the convenience of the number ten. The older metric system included several groups of units...

unit of cal

Calorie

/(mol

Mole (unit)

·K

Kelvin

) for heat capacity, because it offers greater accuracy for single digits.
For an approximate conversion to the corresponding SI unit of J/(mol·K), such values should be multiplied by 4.2 J

Joule

The joule ; symbol J) is a derived unit of energy or work in the International System of Units. It is equal to the energy expended in applying a force of one newton through a distance of one metre , or in passing an electric current of one ampere through a resistance of one ohm for one second...

/cal.

The equipartition of kinetic energy was proposed initially in 1843, and more correctly in 1845, by John James Waterston

John James Waterston

John James Waterston was a Scottish physicist, a neglected pioneer of the kinetic theory of gases.-Early life:Waterston's father, George, was an Edinburgh sealing wax manufacturer and stationer, a relative of the Sandeman family Robert and his brother, George...

. In 1859, James Clerk Maxwell

James Clerk Maxwell

James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...

argued that the kinetic heat energy of a gas is equally divided between linear and rotational energy. In 1876, Ludwig Boltzmann

Ludwig Boltzmann

Ludwig Eduard Boltzmann was an Austrian physicist famous for his founding contributions in the fields of statistical mechanics and statistical thermodynamics...

expanded on this principle by showing that the average energy was divided equally among all the independent components of motion in a system. Boltzmann applied the equipartition theorem to provide a theoretical explanation of the Dulong–Petit law

Dulong–Petit law

for the specific heat capacities of solids.

The history of the equipartition theorem is intertwined with that of specific heat capacity, both of which were studied in the 19th century. In 1819, the French physicists Pierre Louis Dulong

Pierre Louis Dulong

Pierre Louis Dulong was a French physicist and chemist, remembered today largely for the law of Dulong and Petit. He worked on the specific heat capacity and the expansion and refractive indices of gases....

and Alexis Thérèse Petit

Alexis Thérèse Petit

Alexis Thérèse Petit was a French physicist. Petit is known for his work on the efficiencies of air- and steam-engines, published in 1818...

discovered that the specific heat capacities of solid elements at room temperature were inversely proportional to the atomic weight of the element. Their law was used for many years as a technique for measuring atomic weights. However, subsequent studies by James Dewar

James Dewar

Sir James Dewar FRS was a Scottish chemist and physicist. He is probably best-known today for his invention of the Dewar flask, which he used in conjunction with extensive research into the liquefaction of gases...

and Heinrich Friedrich Weber

Heinrich Friedrich Weber

Heinrich Friedrich Weber was a physicist born in the town of Magdala, near Weimar. Around 1861 he entered the University of Jena, where Ernst Abbe became the first of two physicists who decisively influenced his career...

showed that this Dulong–Petit law

Dulong–Petit law

holds only at high temperature

Temperature

s; at lower temperatures, or for exceptionally hard solids such as diamond

Diamond

In mineralogy, diamond is an allotrope of carbon, where the carbon atoms are arranged in a variation of the face-centered cubic crystal structure called a diamond lattice. Diamond is less stable than graphite, but the conversion rate from diamond to graphite is negligible at ambient conditions...

, the specific heat capacity was lower.

Experimental observations of the specific heat capacities of gases also raised concerns about the validity of the equipartition theorem. The theorem predicts that the molar heat capacity of simple monoatomic gases should be roughly 3 cal/(mol·K), whereas that of diatomic gases should be roughly 7 cal/(mol·K). Experiments confirmed the former prediction, but found that molar heat capacities of diatomic gases were typically about 5 cal/(mol·K), and fell to about 3 cal/(mol·K) at very low temperatures. Maxwell

James Clerk Maxwell

noted in 1875 that the disagreement between experiment and the equipartition theorem was much worse than even these numbers suggest; since atoms have internal parts, heat energy should go into the motion of these internal parts, making the predicted specific heats of monoatomic and diatomic gases much higher than 3 cal/(mol·K) and 7 cal/(mol·K), respectively.

A third discrepancy concerned the specific heat of metals. According to the classical Drude model

Drude model

The Drude model of electrical conduction was proposed in 1900 by Paul Drude to explain the transport properties of electrons in materials...

, metallic electrons act as a nearly ideal gas, and so they should contribute (3/2) N_ek_B to the heat capacity by the equipartition theorem, where N_e is the number of electrons. Experimentally, however, electrons contribute little to the heat capacity: the molar heat capacities of many conductors and insulators are nearly the same.

Several explanations of equipartition's failure to account for molar heat capacities were proposed. Boltzmann

Ludwig Boltzmann

Ludwig Eduard Boltzmann was an Austrian physicist famous for his founding contributions in the fields of statistical mechanics and statistical thermodynamics...

defended the derivation of his equipartition theorem as correct, but suggested that gases might not be in thermal equilibrium

Thermal equilibrium

Thermal equilibrium is a theoretical physical concept, used especially in theoretical texts, that means that all temperatures of interest are unchanging in time and uniform in space...

because of their interactions with the aether

Luminiferous aether

In the late 19th century, luminiferous aether or ether, meaning light-bearing aether, was the term used to describe a medium for the propagation of light....

. Lord Kelvin

William Thomson, 1st Baron Kelvin

William Thomson, 1st Baron Kelvin OM, GCVO, PC, PRS, PRSE, was a mathematical physicist and engineer. At the University of Glasgow he did important work in the mathematical analysis of electricity and formulation of the first and second laws of thermodynamics, and did much to unify the emerging...

suggested that the derivation of the equipartition theorem must be incorrect, since it disagreed with experiment, but was unable to show how. In 1900 Lord Rayleigh

John Strutt, 3rd Baron Rayleigh

John William Strutt, 3rd Baron Rayleigh, OM was an English physicist who, with William Ramsay, discovered the element argon, an achievement for which he earned the Nobel Prize for Physics in 1904...

instead put forward a more radical view that the equipartition theorem and the experimental assumption of thermal equilibrium were both correct; to reconcile them, he noted the need for a new principle that would provide an "escape from the destructive simplicity" of the equipartition theorem. Albert Einstein

Albert Einstein

provided that escape, by showing in 1906 that these anomalies in the specific heat were due to quantum effects, specifically the quantization of energy in the elastic modes of the solid. Einstein used the failure of equipartition to argue for the need of a new quantum theory of matter. Nernst's

Walther Nernst

Walther Hermann Nernst FRS was a German physical chemist and physicist who is known for his theories behind the calculation of chemical affinity as embodied in the third law of thermodynamics, for which he won the 1920 Nobel Prize in chemistry...

1910 measurements of specific heats at low temperatures supported Einstein's theory, and led to the widespread acceptance of quantum theory

Quantum mechanics

among physicists.

General formulation of the equipartition theorem

The most general form of the equipartition theorem states that under suitable assumptions (discussed below), for a physical system with Hamiltonian

Hamiltonian (quantum mechanics)

energy function H and degrees of freedom x_n, the following equipartition formula holds in thermal equilibrium for all indices m and n:

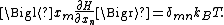
Here δ_mn is the Kronecker delta, which is equal to one if m = n and is zero otherwise. The averaging brackets

is assumed to be an ensemble average

Ensemble average

In statistical mechanics, the ensemble average is defined as the mean of a quantity that is a function of the micro-state of a system , according to the distribution of the system on its micro-states in this ensemble....

over phase space or, under an assumption of ergodicity, a time average of a single system.

The general equipartition theorem holds in both the microcanonical ensemble

Microcanonical ensemble

In statistical physics, the microcanonical ensemble is a theoretical tool used to describe the thermodynamic properties of an isolated system. In such a system, the possible macrostates of the system all have the same energy and the probability for the system to be in any given microstate is the same...

, when the total energy of the system is constant, and also in the canonical ensemble

Canonical ensemble

The canonical ensemble in statistical mechanics is a statistical ensemble representing a probability distribution of microscopic states of the system...

, when the system is coupled to a heat bath with which it can exchange energy. Derivations of the general formula are given later in the article.

The general formula is equivalent to the following two:

If a degree of freedom x_n appears only as a quadratic term a_nx_n² in the Hamiltonian H, then the first of these formulae implies that

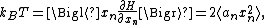
which is twice the contribution that this degree of freedom makes to the average energy

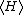. Thus the equipartition theorem for systems with quadratic energies follows easily from the general formula. A similar argument, with 2 replaced by s, applies to energies of the form a_nx_n^s.

The degrees of freedom x_n are coordinates on the phase space

Phase space

In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...

of the system and are therefore commonly subdivided into generalized position

Canonical coordinates

In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...

coordinates q_k and generalized momentum coordinates p_k, where p_k is the conjugate momentum to q_k. In this situation, formula 1 means that for all k,

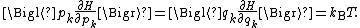
Using the equations of Hamiltonian mechanics

Hamiltonian mechanics

, these formulae may also be written

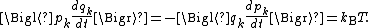
Similarly, one can show using formula 2 that

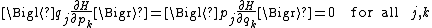
and

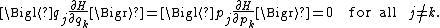
Relation to the virial theorem

The general equipartition theorem is an extension of the virial theorem (proposed in 1870), which states that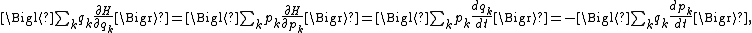

where t denotes time

Time

Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....

. Two key differences are that the virial theorem relates summed rather than individual averages to each other, and it does not connect them to the temperature

Temperature

T. Another difference is that traditional derivations of the virial theorem use averages over time, whereas those of the equipartition theorem use averages over phase space

Phase space

Ideal gas law

Ideal gas

es provide an important application of the equipartition theorem. As well as providing the formula

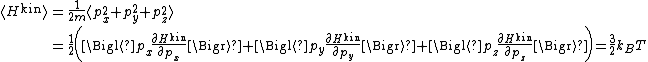
for the average kinetic energy per particle, the equipartition theorem can be used to derive the ideal gas law

Ideal gas law

from classical mechanics. If q = (q_x, q_y, q_z) and p = (p_x, p_y, p_z) denote the position vector and momentum of a particle in the gas, and
F is the net force on that particle, then

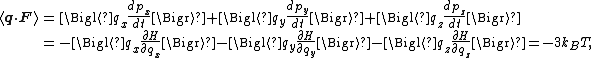
where the first equality is Newton's second law, and the second line uses Hamilton's equations and the equipartition formula. Summing over a system of N particles yields

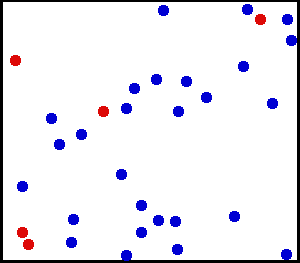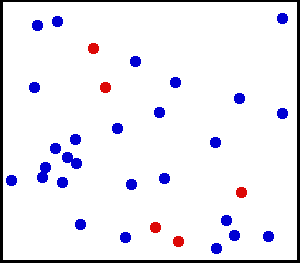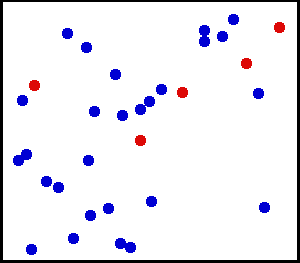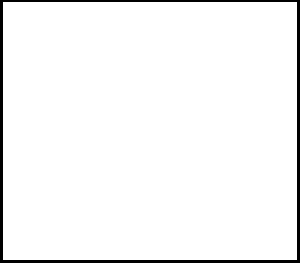
By Newton's third law and the ideal gas assumption, the net force on the system is the force applied by the walls of their container, and this force is given by the pressure P of the gas. Hence

where dS is the infinitesimal area element along the walls of the container. Since the divergence

Divergence

In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...

of the position vector q is

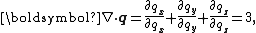
the divergence theorem

Divergence theorem

In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...

implies that

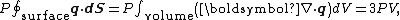
where dV is an infinitesimal volume within the container and V is the total volume of the container.

Putting these equalities together yields

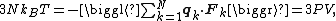
which immediately implies the ideal gas law
Ideal gas law
The ideal gas law is the equation of state of a hypothetical ideal gas. It is a good approximation to the behavior of many gases under many conditions, although it has several limitations. It was first stated by Émile Clapeyron in 1834 as a combination of Boyle's law and Charles's law...

for N particles:

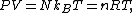
where n = N/N_A is the number of moles of gas and R = N_Ak_B is the gas constant

Gas constant

. Although equipartition provides a simple derivation of the ideal-gas law and the internal energy, the same results can be obtained by an alternative method using the partition function

Partition function (statistical mechanics)

Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...

Diatomic gases

A diatomic gas can be modelled as two masses, m₁ and m₂, joined by a spring
Spring (device)
A spring is an elastic object used to store mechanical energy. Springs are usually made out of spring steel. Small springs can be wound from pre-hardened stock, while larger ones are made from annealed steel and hardened after fabrication...

of stiffness
Hooke's law
In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...

a, which is called the rigid rotor-harmonic oscillator approximation. The classical energy of this system is

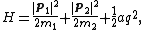
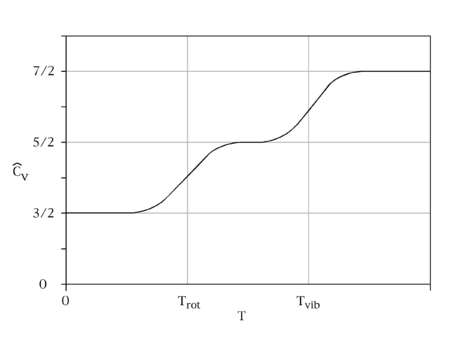
where p₁ and p₂ are the momenta of the two atoms, and q is the deviation of the inter-atomic separation from its equilibrium value. Every degree of freedom in the energy is quadratic and, thus, should contribute k_BT to the total average energy, and k_B to the heat capacity. Therefore, the heat capacity of a gas of N diatomic molecules is predicted to be 7N·k_B: the momenta p₁ and p₂ contribute three degrees of freedom each, and the extension q contributes the seventh. It follows that the heat capacity of a mole of diatomic molecules with no other degrees of freedom should be (7/2)N_Ak_B = (7/2)R and, thus, the predicted molar heat capacity should be roughly 7 cal/(mol·K). However, the experimental values for molar heat capacities of diatomic gases are typically about 5 cal/(mol·K) and fall to 3 cal/(mol·K) at very low temperatures. This disagreement between the equipartition prediction and the experimental value of the molar heat capacity cannot be explained by using a more complex model of the molecule, since adding more degrees of freedom can only increase the predicted specific heat, not decrease it. This discrepancy was a key piece of evidence showing the need for a quantum theory

Quantum mechanics

of matter.

Extreme relativistic ideal gases

Equipartition was used above to derive the classical ideal gas law

Ideal gas law

from Newtonian mechanics. However, relativistic effects

Special relativity

become dominant in some systems, such as white dwarf

White dwarf

s and neutron star

Neutron star

s, and the ideal gas equations must be modified. The equipartition theorem provides a convenient way to derive the corresponding laws for an extreme relativistic ideal gas

Ideal gas

. In such cases, the kinetic energy of a single particle

Relativistic particle

A relativistic particle is a particle which moves with a relativistic speed; that is, a speed comparable to the speed of light. This is achieved by photons to the extent that effects described by special relativity are able to describe those of such particles themselves...

is given by the formula

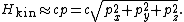
Taking the derivative of H with respect to the p_x momentum component gives the formula

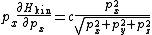
and similarly for the p_y and p_z components. Adding the three components together gives

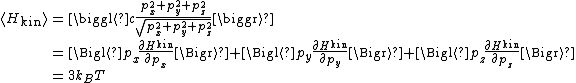
where the last equality follows from the equipartition formula. Thus, the average total energy of an extreme relativistic gas is twice that of the non-relativistic case: for N particles, it is 3 Nk_BT.

Non-ideal gases
In an ideal gas the particles are assumed to interact only through collisions. The equipartition theorem may also be used to derive the energy and pressure of "non-ideal gases" in which the particles also interact with one another through conservative force
Conservative force
A conservative force is a force with the property that the work done in moving a particle between two points is independent of the path taken. Equivalently, if a particle travels in a closed loop, the net work done by a conservative force is zero.It is possible to define a numerical value of...

s whose potential U(r) depends only on the distance r between the particles. This situation can be described by first restricting attention to a single gas particle, and approximating the rest of the gas by a spherically symmetric distribution. It is then customary to introduce a radial distribution function
Radial distribution function
In statistical mechanics, a radial distribution function , g, describes how the atomic density varies as a function of the distance from one particular atom....

g(r) such that the probability density
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...

of finding another particle at a distance r from the given particle is equal to 4πr²ρg(r), where ρ = N/V is the mean density

Density

The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...

of the gas. It follows that the mean potential energy associated to the interaction of the given particle with the rest of the gas is

The total mean potential energy of the gas is therefore

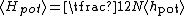, where N is the number of particles in the gas, and the factor is needed because summation over all the particles counts each interaction twice.
Adding kinetic and potential energies, then applying equipartition, yields the energy equation

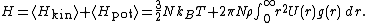
A similar argument, can be used to derive the pressure equation

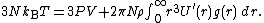
Anharmonic oscillators
An anharmonic oscillator (in contrast to a simple harmonic oscillator) is one in which the potential energy is not quadratic in the extension q (the generalized position which measures the deviation of the system from equilibrium). Such oscillators provide a complementary point of view on the equipartition theorem. Simple examples are provided by potential energy functions of the form

where C and s are arbitrary real constants
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

. In these cases, the law of equipartition predicts that

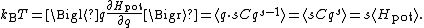
Thus, the average potential energy equals k_BT/s, not k_BT/2 as for the quadratic harmonic oscillator (where s = 2).

More generally, a typical energy function of a one-dimensional system has a Taylor expansion in the extension q:

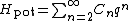
for non-negative integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

s n. There is no n = 1 term, because at the equilibrium point, there is no net force and so the first derivative of the energy is zero. The n = 0 term need not be included, since the energy at the equilibrium position may be set to zero by convention. In this case, the law of equipartition predicts that

In contrast to the other examples cited here, the equipartition formula

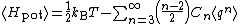
does not allow the average potential energy to be written in terms of known constants.

Brownian motion

The equipartition theorem can be used to derive the Brownian motion

Brownian motion

Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...

of a particle from the Langevin equation

Langevin equation

In statistical physics, a Langevin equation is a stochastic differential equation describing the time evolution of a subset of the degrees of freedom. These degrees of freedom typically are collective variables changing only slowly in comparison to the other variables of the system...

. According to that equation, the motion of a particle of mass m with velocity v is governed by Newton's second law

Newton's laws of motion

Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...

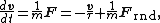
where F_rnd is a random force representing the random collisions of the particle and the surrounding molecules, and where the time constant

Time constant

In physics and engineering, the time constant, usually denoted by the Greek letter \tau , is the risetime characterizing the response to a time-varying input of a first-order, linear time-invariant system.Concretely, a first-order LTI system is a system that can be modeled by a single first order...

τ reflects the drag force

Drag (physics)

In fluid dynamics, drag refers to forces which act on a solid object in the direction of the relative fluid flow velocity...

that opposes the particle's motion through the solution. The drag force is often written F_drag = −γv; therefore, the time constant τ equals m/γ.

The dot product of this equation with the position vector r, after averaging, yields the equation

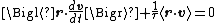
for Brownian motion (since the random force F_rnd is uncorrelated with the position r). Using the mathematical identities

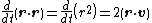
and

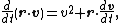
the basic equation for Brownian motion can be transformed into

where the last equality follows from the equipartition theorem for translational kinetic energy:

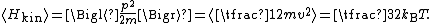
The above differential equation

Differential equation

A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...

for

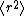(with suitable initial conditions) may be solved exactly: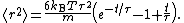

On small time scales, with t << τ, the particle acts as a freely moving particle: by the Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....

of the exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...

, the squared distance grows approximately quadratically:

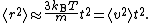
However, on long time scales, with t >> τ, the exponential and constant terms are negligible, and the squared distance grows only linearly:

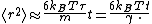
This describes the diffusion

Diffusion

of the particle over time. An analogous equation for the rotational diffusion of a rigid molecule can be derived in a similar way.

Stellar physics

The equipartition theorem and the related virial theorem have long been used as a tool in astrophysics

Astrophysics

Astrophysics is the branch of astronomy that deals with the physics of the universe, including the physical properties of celestial objects, as well as their interactions and behavior...

. As examples, the virial theorem may be used to estimate stellar temperatures or the Chandrasekhar limit

Chandrasekhar limit

When a star starts running out of fuel, it usually cools off and collapses into one of three compact forms, depending on its total mass:* a White Dwarf, a big lump of Carbon and Oxygen atoms, almost like one huge molecule...

on the mass of white dwarf

White dwarf

stars.

The average temperature of a star can be estimated from the equipartition theorem. Since most stars are spherically symmetric, the total gravitational

Newton's law of universal gravitation

Newton's law of universal gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them...

potential energy can be estimated by integration

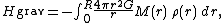
where M(r) is the mass within a radius r and ρ(r) is the stellar density at radius r; G represents the gravitational constant
Gravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...

and R the total radius of the star. Assuming a constant density throughout the star, this integration yields the formula

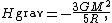
where M is the star's total mass. Hence, the average potential energy of a single particle is

where N is the number of particles in the star. Since most star
Star
A star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...

s are composed mainly of ion
Ion
An ion is an atom or molecule in which the total number of electrons is not equal to the total number of protons, giving it a net positive or negative electrical charge. The name was given by physicist Michael Faraday for the substances that allow a current to pass between electrodes in a...

ized hydrogen
Hydrogen
Hydrogen is the chemical element with atomic number 1. It is represented by the symbol H. With an average atomic weight of , hydrogen is the lightest and most abundant chemical element, constituting roughly 75% of the Universe's chemical elemental mass. Stars in the main sequence are mainly...

, N equals roughly M/m_p, where m_p is the mass of one proton. Application of the equipartition theorem gives an estimate of the star's temperature

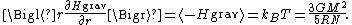
Substitution of the mass and radius of the Sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...

yields an estimated solar temperature of T = 14 million kelvins, very close to its core temperature of 15 million kelvins. However, the Sun is much more complex than assumed by this model—both its temperature and density vary strongly with radius—and such excellent agreement (≈7% relative error

Approximation error

The approximation error in some data is the discrepancy between an exact value and some approximation to it. An approximation error can occur because#the measurement of the data is not precise due to the instruments...

) is partly fortuitous.

Star formation

The same formulae may be applied to determining the conditions for star formation

Star formation

Star formation is the process by which dense parts of molecular clouds collapse into a ball of plasma to form a star. As a branch of astronomy star formation includes the study of the interstellar medium and giant molecular clouds as precursors to the star formation process and the study of young...

in giant molecular cloud

Molecular cloud

A molecular cloud, sometimes called a stellar nursery if star formation is occurring within, is a type of interstellar cloud whose density and size permits the formation of molecules, most commonly molecular hydrogen ....

s. A local fluctuation in the density of such a cloud can lead to a runaway condition in which the cloud collapses inwards under its own gravity. Such a collapse occurs when the equipartition theorem—or, equivalently, the virial theorem—is no longer valid, i.e., when the gravitational potential energy exceeds twice the kinetic energy

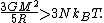
Assuming a constant density ρ for the cloud

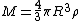
yields a minimum mass for stellar contraction, the Jeans mass M_J

Substituting the values typically observed in such clouds (T = 150 K, ρ = 2 g/cm³) gives an estimated minimum mass of 17 solar masses, which is consistent with observed star formation. This effect is also known as the Jeans instability

Jeans instability

In physics, the Jeans instability causes the collapse of interstellar gas clouds and subsequent star formation. It occurs when the internal gas pressure is not strong enough to prevent gravitational collapse of a region filled with matter...

, after the British physicist James Hopwood Jeans

James Hopwood Jeans

Sir James Hopwood Jeans OM FRS MA DSc ScD LLD was an English physicist, astronomer and mathematician.-Background:...

who published it in 1902.

Kinetic energies and the Maxwell–Boltzmann distribution

The original formulation of the equipartition theorem states that, in any physical system in thermal equilibrium

Thermal equilibrium

Thermal equilibrium is a theoretical physical concept, used especially in theoretical texts, that means that all temperatures of interest are unchanging in time and uniform in space...

, every particle has exactly the same average kinetic energy

Kinetic energy

, (3/2)k_BT. This may be shown using the Maxwell–Boltzmann distribution (see Figure 2), which is the probability distribution

for the speed of a particle of mass m in the system, where the speed v is the magnitude of the velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...

vector

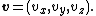
The Maxwell–Boltzmann distribution applies to any system composed of atoms, and assumes only a canonical ensemble
Canonical ensemble
The canonical ensemble in statistical mechanics is a statistical ensemble representing a probability distribution of microscopic states of the system...

, specifically, that the kinetic energies are distributed according to their Boltzmann factor
Boltzmann factor
In physics, the Boltzmann factor is a weighting factor that determines the relative probability of a particle to be in a state i in a multi-state system in thermodynamic equilibrium at temperature T...

at a temperature T. The average kinetic energy for a particle of mass m is then given by the integral formula

as stated by the equipartition theorem. The same result can also be obtained by averaging the particle energy using the probability of finding the particle in certain quantum energy state.

Quadratic energies and the partition function

More generally, the equipartition theorem states that any degree of freedom

Degrees of freedom (physics and chemistry)

A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...

x which appears in the total energy H only as a simple quadratic term Ax², where A is a constant, has an average energy of ½k_BT in thermal equilibrium. In this case the equipartition theorem may be derived from the partition function
Partition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...

Z(β), where β = 1/(k_BT) is the canonical inverse temperature. Integration over the variable x yields a factor

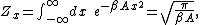
in the formula for Z. The mean energy associated with this factor is given by

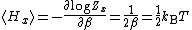
as stated by the equipartition theorem.

General proofs

General derivations of the equipartition theorem can be found in many statistical mechanics

Statistical mechanics

Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...

textbooks, both for the microcanonical ensemble

Microcanonical ensemble

and for the canonical ensemble

Canonical ensemble

The canonical ensemble in statistical mechanics is a statistical ensemble representing a probability distribution of microscopic states of the system...

.
They involve taking averages over the phase space

Phase space

of the system, which is a symplectic manifold

Symplectic manifold

In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...

.

To explain these derivations, the following notation is introduced. First, the phase space is described in terms of generalized position coordinates

Canonical coordinates

qj together with their conjugate momenta pj. The quantities qj completely describe the configuration
Configuration space
- Configuration space in physics :In classical mechanics, the configuration space is the space of possible positions that a physical system may attain, possibly subject to external constraints...

of the system, while the quantities (qj,pj) together completely describe its state
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...

.

Secondly, the infinitesimal volume
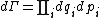
of the phase space is introduced and used to define the volume Γ(E, ΔE) of the portion of phase space where the energy H of the system lies between two limits, E and E+ΔE:

In this expression, ΔE is assumed to be very small, ΔE << E. Similarly, Σ(E) is defined to be the total volume of phase space where the energy is less than E:

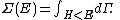
Since ΔE is very small, the following integrations are equivalent

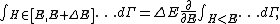
where the ellipses represent the integrand. From this, it follows that Γ is proportional to ΔE

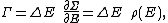
where ρ(E) is the density of states
Density of states
In solid-state and condensed matter physics, the density of states of a system describes the number of states per interval of energy at each energy level that are available to be occupied by electrons. Unlike isolated systems, like atoms or molecules in gas phase, the density distributions are not...

. By the usual definitions of statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...

, the entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...

S equals k_B log Σ(E), and the temperature

Temperature

T is defined by

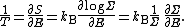
The canonical ensemble

In the canonical ensemble

Canonical ensemble

The canonical ensemble in statistical mechanics is a statistical ensemble representing a probability distribution of microscopic states of the system...

, the system is in thermal equilibrium

Thermal equilibrium

Thermal equilibrium is a theoretical physical concept, used especially in theoretical texts, that means that all temperatures of interest are unchanging in time and uniform in space...

with an infinite heat bath at temperature

Temperature

T (in kelvins). The probability of each state in phase space

Phase space

is given by its Boltzmann factor

Boltzmann factor

In physics, the Boltzmann factor is a weighting factor that determines the relative probability of a particle to be in a state i in a multi-state system in thermodynamic equilibrium at temperature T...

times a normalization factor

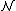, which is chosen so that the probabilities sum to one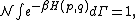

where β = 1/k_BT. Integration by parts

Integration by parts

In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...

for a phase-space variable x_k (which could be either q_k or p_k) between two limits a and b yields the equation

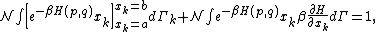
where dΓ_k = dΓ/dx_k, i.e., the first integration is not carried out over x_k. The first term is usually zero, either because x_k is zero at the limits, or because the energy goes to infinity at those limits. In that case, the equipartition theorem for the canonical ensemble follows immediately

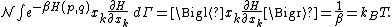
Here, the averaging symbolized by

is the ensemble average

Ensemble average

taken over the canonical ensemble

Canonical ensemble

The canonical ensemble in statistical mechanics is a statistical ensemble representing a probability distribution of microscopic states of the system...

The microcanonical ensemble

In the microcanonical ensemble, the system is isolated from the rest of the world, or at least very weakly coupled to it. Hence, its total energy is effectively constant; to be definite, we say that the total energy H is confined between E and E+dE. For a given energy E and spread dE, there is a region of phase space

Phase space

Γ in which the system has that energy, and the probability of each state in that region of phase space

Phase space

is equal, by the definition of the microcanonical ensemble. Given these definitions, the equipartition average of phase-space variables x_m (which could be either q_kor p_k) and x_n is given by

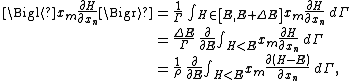
where the last equality follows because E is a constant that does not depend on x_n. Integrating by parts

Integration by parts

In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...

yields the relation

since the first term on the right hand side of the first line is zero (it can be rewritten as an integral of H − E on the hypersurface

Hypersurface

In geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...

where H = E).

Substitution of this result into the previous equation yields

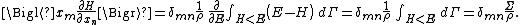
Since

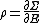the equipartition theorem follows: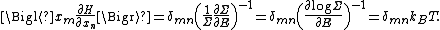

Thus, we have derived the general formulation of the equipartition theorem
which was so useful in the applications described above.

Limitations

Requirement of ergodicity

The law of equipartition holds only for ergodic

Ergodic hypothesis

In physics and thermodynamics, the ergodic hypothesis says that, over long periods of time, the time spent by a particle in some region of the phase space of microstates with the same energy is proportional to the volume of this region, i.e., that all accessible microstates are equiprobable over a...

systems in thermal equilibrium

Thermal equilibrium

Thermal equilibrium is a theoretical physical concept, used especially in theoretical texts, that means that all temperatures of interest are unchanging in time and uniform in space...

, which implies that all states with the same energy must be equally likely to be populated. Consequently, it must be possible to exchange energy among all its various forms within the system, or with an external heat bath in the canonical ensemble

Canonical ensemble

The canonical ensemble in statistical mechanics is a statistical ensemble representing a probability distribution of microscopic states of the system...

. The number of physical systems that have been rigorously proven to be ergodic is small; a famous example is the hard-sphere system

Dynamical billiards

A billiard is a dynamical system in which a particle alternates between motion in a straight line and specular reflections from a boundary. When the particle hits the boundary it reflects from it without loss of speed...

of Yakov Sinai

Yakov G. Sinai

Yakov Grigorevich Sinai is an influential mathematician working in the theory of dynamical systems, in mathematical physics and in probability theory. His work has shaped the modern metric theory of dynamical systems...

. The requirements for isolated systems to ensure ergodicity

Ergodic theory

Ergodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....

—and, thus equipartition—have been studied, and provided motivation for the modern chaos theory

Chaos theory

Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...

of dynamical system

Dynamical system

A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...

s. A chaotic Hamiltonian system

Hamiltonian system

In physics and classical mechanics, a Hamiltonian system is a physical system in which forces are momentum invariant. Hamiltonian systems are studied in Hamiltonian mechanics....

need not be ergodic, although that is usually a good assumption.

A commonly cited counter-example where energy is not shared among its various forms and where equipartition does not hold in the microcanonical ensemble is a system of coupled harmonic oscillators. If the system is isolated from the rest of the world, the energy in each normal mode

Normal mode

is constant; energy is not transferred from one mode to another. Hence, equipartition does not hold for such a system; the amount of energy in each normal mode is fixed at its initial value. If sufficiently strong nonlinear terms are present in the energy

Energy

In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...

function, energy may be transferred between the normal modes, leading to ergodicity and rendering the law of equipartition valid. However, the Kolmogorov–Arnold–Moser theorem

Kolmogorov–Arnold–Moser theorem

The Kolmogorov–Arnold–Moser theorem is a result in dynamical systems about the persistence of quasi-periodic motions under small perturbations. The theorem partly resolves the small-divisor problem that arises in the perturbation theory of classical mechanics....

states that energy will not be exchanged unless the nonlinear perturbations are strong enough; if they are too small, the energy will remain trapped in at least some of the modes.

Another way ergodicity can be broken is by the existence of nonlinear soliton

Soliton

In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...

symmetries. In 1953, Fermi

Enrico Fermi

Enrico Fermi was an Italian-born, naturalized American physicist particularly known for his work on the development of the first nuclear reactor, Chicago Pile-1, and for his contributions to the development of quantum theory, nuclear and particle physics, and statistical mechanics...

, Pasta

John Pasta

John R. Pasta was a computer scientist who is remembered today for the Fermi–Pasta–Ulam experiment, a result much discussed among physicists and researchers in dynamical systems and chaos theory, and as the head of the department of Computer Science at the University of Illinois at...

, Ulam

Stanislaw Marcin Ulam

Stanisław Marcin Ulam was a renowned mathematician of Polish-Jewish origin. He participated in America's Manhattan Project, originated the Teller–Ulam design of thermonuclear weapons, invented the Monte Carlo method of computation, and proposed the idea of nuclear pulse propulsion...

and Mary Tsingou conducted computer simulations of a vibrating string that included a non-linear term (quadratic in one test, cubic in another, and a piecewise linear approximation to a cubic in a third). They found that the behavior of the system was quite different from what intuition based on equipartition would have led them to expect. Instead of the energies in the modes becoming equally shared, the system exhibited a very complicated quasi-periodic behavior. This puzzling result was eventually explained by Kruskal and Zabusky in 1965 in a paper which, by connecting the simulated system to the Korteweg–de Vries equation

Korteweg–de Vries equation

In mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified...

led to the development of soliton mathematics.

Failure due to quantum effects

The law of equipartition breaks down when the thermal energy k_BT is significantly smaller than the spacing between energy levels. Equipartition no longer holds because it is a poor approximation to assume that the energy levels form a smooth continuum

Continuum (theory)

Continuum theories or models explain variation as involving a gradual quantitative transition without abrupt changes or discontinuities. It can be contrasted with 'categorical' models which propose qualitatively different states.-In physics:...

, which is required in the derivations of the equipartition theorem above. Historically, the failures of the classical equipartition theorem to explain specific heats and blackbody radiation were critical in showing the need for a new theory of matter and radiation, namely, quantum mechanics

Quantum mechanics

and quantum field theory

Quantum field theory

To illustrate the breakdown of equipartition, consider the average energy in a single (quantum) harmonic oscillator, which was discussed above for the classical case. Neglecting the irrelevant zero-point energy

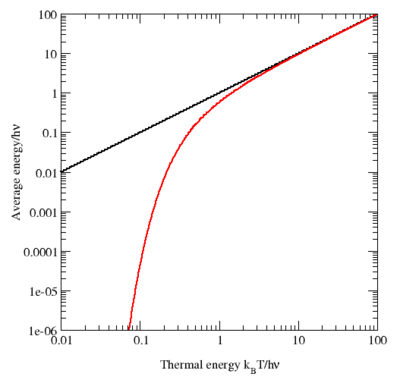
Zero-point energy

Zero-point energy is the lowest possible energy that a quantum mechanical physical system may have; it is the energy of its ground state. All quantum mechanical systems undergo fluctuations even in their ground state and have an associated zero-point energy, a consequence of their wave-like nature...

term, its quantum energy levels are given by E_n = nhν, where h is the Planck constant

Planck constant

The Planck constant , also called Planck's constant, is a physical constant reflecting the sizes of energy quanta in quantum mechanics. It is named after Max Planck, one of the founders of quantum theory, who discovered it in 1899...

, ν is the fundamental frequency

Fundamental frequency

The fundamental frequency, often referred to simply as the fundamental and abbreviated f0, is defined as the lowest frequency of a periodic waveform. In terms of a superposition of sinusoids The fundamental frequency, often referred to simply as the fundamental and abbreviated f0, is defined as the...

of the oscillator, and n is an integer. The probability of a given energy level being populated in the canonical ensemble

Canonical ensemble

The canonical ensemble in statistical mechanics is a statistical ensemble representing a probability distribution of microscopic states of the system...

is given by its Boltzmann factor

Boltzmann factor

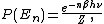
where β = 1/k_BT and the denominator Z is the partition function

Partition function (statistical mechanics)

Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...

, here a geometric series

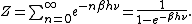
Its average energy is given by

Substituting the formula for Z gives the final result

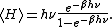
At high temperatures, when the thermal energy k_BT is much greater than the spacing hν between energy levels, the exponential argument βhν is much less than one and the average energy becomes k_BT, in agreement with the equipartition theorem (Figure 10). However, at low temperatures, when hν >> k_BT, the average energy goes to zero—the higher-frequency energy levels are "frozen out" (Figure 10). As another example, the internal excited electronic states of a hydrogen atom do not contribute to its specific heat as a gas at room temperature, since the thermal energy k_BT (roughly 0.025 eV

Electronvolt

In physics, the electron volt is a unit of energy equal to approximately joule . By definition, it is equal to the amount of kinetic energy gained by a single unbound electron when it accelerates through an electric potential difference of one volt...

) is much smaller than the spacing between the lowest and next higher electronic energy levels (roughly 10 eV).

Similar considerations apply whenever the energy level spacing is much larger than the thermal energy. For example, this reasoning was used by Albert Einstein

Albert Einstein

to resolve the ultraviolet catastrophe

Ultraviolet catastrophe

of blackbody radiation. The paradox arises because there are an infinite number of independent modes of the electromagnetic field

Electromagnetic field

An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...

in a closed container, each of which may be treated as a harmonic oscillator. If each electromagnetic mode were to have an average energy k_BT, there would be an infinite amount of energy in the container. However, by the reasoning above, the average energy in the higher-frequency modes goes to zero as ν goes to infinity; moreover, Planck's law of black body radiation

Planck's law of black body radiation

In physics, Planck's law describes the amount of energy emitted by a black body in radiation of a certain wavelength . The law is named after Max Planck, who originally proposed it in 1900. The law was the first to accurately describe black body radiation, and resolved the ultraviolet catastrophe...

, which describes the experimental distribution of energy in the modes, follows from the same reasoning.

Other, more subtle quantum effects can lead to corrections to equipartition, such as identical particles

Identical particles

Identical particles, or indistinguishable particles, are particles that cannot be distinguished from one another, even in principle. Species of identical particles include elementary particles such as electrons, and, with some clauses, composite particles such as atoms and molecules.There are two...

and continuous symmetries

Symmetry

Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...

. The effects of identical particles can be dominant at very high densities and low temperatures. For example, the valence electron

Valence electron

In chemistry, valence electrons are the electrons of an atom that can participate in the formation of chemical bonds with other atoms. Valence electrons are the "own" electrons, present in the free neutral atom, that combine with valence electrons of other atoms to form chemical bonds. In a single...

s in a metal can have a mean kinetic energy of a few electronvolt

Electronvolt

s, which would normally correspond to a temperature of tens of thousands of kelvins. Such a state, in which the density is high enough that the Pauli exclusion principle

Pauli exclusion principle

The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...

invalidates the classical approach, is called a degenerate fermion gas

Degenerate matter

Degenerate matter is matter that has such extraordinarily high density that the dominant contribution to its pressure is attributable to the Pauli exclusion principle. The pressure maintained by a body of degenerate matter is called the degeneracy pressure, and arises because the Pauli principle...

. Such gases are important for the structure of white dwarf

White dwarf

and neutron star

Neutron star

s. At low temperatures, a fermionic analogue

Fermionic condensate

A fermionic condensate is a superfluid phase formed by fermionic particles at low temperatures. It is closely related to the Bose–Einstein condensate, a superfluid phase formed by bosonic atoms under similar conditions. Unlike the Bose–Einstein condensates, fermionic condensates are formed using...

of the Bose–Einstein condensate

Bose–Einstein condensate

A Bose–Einstein condensate is a state of matter of a dilute gas of weakly interacting bosons confined in an external potential and cooled to temperatures very near absolute zero . Under such conditions, a large fraction of the bosons occupy the lowest quantum state of the external potential, at...

(in which a large number of identical particles occupy the lowest-energy state) can form; such superfluid

Superfluid

Superfluidity is a state of matter in which the matter behaves like a fluid without viscosity and with extremely high thermal conductivity. The substance, which appears to be a normal liquid, will flow without friction past any surface, which allows it to continue to circulate over obstructions and...

electrons are responsible for superconductivity

Superconductivity

Superconductivity is a phenomenon of exactly zero electrical resistance occurring in certain materials below a characteristic temperature. It was discovered by Heike Kamerlingh Onnes on April 8, 1911 in Leiden. Like ferromagnetism and atomic spectral lines, superconductivity is a quantum...

External links

Applet demonstrating equipartition in real time for a mixture of monatomic and diatomic gases
The equipartition theorem in stellar physics, written by Nir J. Shaviv, an associate professor at the Racah Institute of Physics in the Hebrew University of Jerusalem
Hebrew University of Jerusalem
The Hebrew University of Jerusalem ; ; abbreviated HUJI) is Israel's second-oldest university, after the Technion – Israel Institute of Technology. The Hebrew University has three campuses in Jerusalem and one in Rehovot. The world's largest Jewish studies library is located on its Edmond J...

.

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.