.gif)
Degrees of freedom (physics and chemistry)
Encyclopedia
A degree of freedom is an independent physical parameter, often called a dimension
, in the formal description of the state of a physical system
. The set of all dimensions of a system is known as a phase space
.
, a degree of freedom of a system is a formal description of a parameter that contributes to the state of a physical system.
In mechanics, a point particle can move independently in the three directions of space. Thus, the momentum of a particle consists of three components, each called a degree of freedom. A system of N independent particles, therefore, has the total of 3N degrees of freedom.
Similarly in statistical mechanics
, a degree of freedom is a single scalar
number describing the microstate
of a system. The specification of all microstates of a system is a point in the system's phase space
.
A degree of freedom may be any useful property that is not dependent on other variables. For example, in the 3D ideal chain
model, two angles are necessary to describe each monomer's orientation.
.png) In three-dimensional space, three degrees of freedom are associated with the movement of a mechanical particle. A diatomic gas molecule thus has 6 degrees of freedom. This set may be decomposed in terms of translations, rotations, and vibrations of the molecule. The center of mass motion of the entire molecule accounts for 3 degrees of freedom. In addition, the molecule has one vibrational mode and two rotational degrees of motion. The rotations occur around the two axes perpendicular to the line between the two atoms. The rotation around the atom-atom bond is not counted. This yields, for a diatomic molecule, a decomposition of:
In three-dimensional space, three degrees of freedom are associated with the movement of a mechanical particle. A diatomic gas molecule thus has 6 degrees of freedom. This set may be decomposed in terms of translations, rotations, and vibrations of the molecule. The center of mass motion of the entire molecule accounts for 3 degrees of freedom. In addition, the molecule has one vibrational mode and two rotational degrees of motion. The rotations occur around the two axes perpendicular to the line between the two atoms. The rotation around the atom-atom bond is not counted. This yields, for a diatomic molecule, a decomposition of:
For a general molecule with N > 2 atoms, all 3 rotational degrees of freedom are considered, resulting in the decomposition:
which means that an N-atom molecule has 3N - 6 vibrational degrees of freedom for N > 2.
Contrary to the classical equipartition theorem, at room temperature, the vibrational motion of molecules typically makes negligible contributions to the heat capacity
. This is because these degrees of freedom are frozen because the spacing between the energy eigenvalues exceeds the energy corresponding to ambient temperatures (kT). In the following table such degrees of freedom are disregarded because of their low effect on total energy. However, at very high temperatures they cannot be neglected.
 of a system is independent if the energy associated with the set can be written in the following form:
of a system is independent if the energy associated with the set can be written in the following form:
where is a function of the sole variable
is a function of the sole variable  .
.
example: if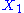 and
and 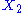 are two degrees of freedom, and
are two degrees of freedom, and  is the associated energy:
is the associated energy:
At thermodynamic equilibrium
, are all statistically independent
are all statistically independent
of each other.
For i from 1 to N, the value of the ith degree of freedom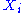 is distributed according to the Boltzmann distribution
is distributed according to the Boltzmann distribution
. Its probability density function
is the following:
In this section, and throughout the article the brackets denote the mean
denote the mean
of the quantity they enclose.
The internal energy
of the system is the sum of the average energies associated to each of the degrees of freedom: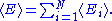
, a result that is demonstrated for a system in a particular ensemble remains true for this system at the thermodynamic limit
in any ensemble. In the canonical ensemble, at thermodynamic equilibrium
, the state of the system is distributed among all micro-states
according to the Boltzmann distribution
. If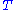 is the system's temperature
is the system's temperature
and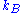 is Boltzmann's constant, then the probability density function
is Boltzmann's constant, then the probability density function
associated to each micro-state is the following:
The denominator in the above expression plays an important role. This expression immediately breaks down into a product of terms depending of a single degree of freedom: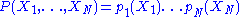
The existence of such a breakdown of the multidimensional probability density function
into a product of functions of one variable is enough by itself to demonstrate that are statistically independent
are statistically independent
from each other.
Since each function is normalized
is normalized
, it follows immediately that is the probability density function
is the probability density function
of the degree of freedom , for i from 1 to N.
, for i from 1 to N.
Finally, the internal energy
of the system is its mean
energy. The energy of a degree of freedom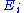 is a function of the sole variable
is a function of the sole variable 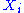 . Since
. Since  are independent
are independent
from each other, the energies
 are also statistically independent
are also statistically independent
from each other. The total internal energy
of the system can thus be written as: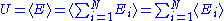
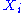 is quadratic if the energy terms associated to this degree of freedom can be written as
is quadratic if the energy terms associated to this degree of freedom can be written as ,
,
where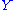 is a linear combination
is a linear combination
of other quadratic degrees of freedom.
example: if and
and 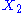 are two degrees of freedom, and
are two degrees of freedom, and  is the associated energy:
is the associated energy:
For example, in Newtonian mechanics, the dynamics
of a system of quadratic degrees of freedom are controlled by a set of homogeneous linear differential equation
s with constant coefficients
.
 are quadratic and independent degrees of freedom if the energy associated to a microstate of the system they represent can be written as:
are quadratic and independent degrees of freedom if the energy associated to a microstate of the system they represent can be written as: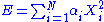
, at thermodynamic equilibrium
, the internal energy
of a system of N quadratic and independent degrees of freedom is:
Here, the mean
energy associated with a degree of freedom is: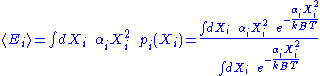
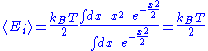
Since the degrees of freedom are independent, the internal energy
of the system is equal to the sum of the mean
energy associated with each degree of freedom, which demonstrates the result.
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
, in the formal description of the state of a physical system
Physical system
In physics, the word system has a technical meaning, namely, it is the portion of the physical universe chosen for analysis. Everything outside the system is known as the environment, which in analysis is ignored except for its effects on the system. The cut between system and the world is a free...
. The set of all dimensions of a system is known as a phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
.
Definition
In physicsPhysics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, a degree of freedom of a system is a formal description of a parameter that contributes to the state of a physical system.
In mechanics, a point particle can move independently in the three directions of space. Thus, the momentum of a particle consists of three components, each called a degree of freedom. A system of N independent particles, therefore, has the total of 3N degrees of freedom.
Similarly in statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, a degree of freedom is a single scalar
Scalar (physics)
In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations , or by Lorentz transformations or space-time translations . This is in contrast to a vector...
number describing the microstate
Microstate (statistical mechanics)
In statistical mechanics, a microstate is a specific microscopic configuration of a thermodynamic system that the system may occupy with a certain probability in the course of its thermal fluctuations...
of a system. The specification of all microstates of a system is a point in the system's phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
.
A degree of freedom may be any useful property that is not dependent on other variables. For example, in the 3D ideal chain
Ideal chain
An ideal chain is the simplest model to describe a polymer. It only assumes a polymer as a random walk and neglects any kind of interactions among monomers...
model, two angles are necessary to describe each monomer's orientation.
Example: diatomic gas
.png)
- 3N = 6 = .
For a general molecule with N > 2 atoms, all 3 rotational degrees of freedom are considered, resulting in the decomposition:
- 3 N = 3 + 3 + (3 N - 6)
which means that an N-atom molecule has 3N - 6 vibrational degrees of freedom for N > 2.
Contrary to the classical equipartition theorem, at room temperature, the vibrational motion of molecules typically makes negligible contributions to the heat capacity
Heat capacity
Heat capacity , or thermal capacity, is the measurable physical quantity that characterizes the amount of heat required to change a substance's temperature by a given amount...
. This is because these degrees of freedom are frozen because the spacing between the energy eigenvalues exceeds the energy corresponding to ambient temperatures (kT). In the following table such degrees of freedom are disregarded because of their low effect on total energy. However, at very high temperatures they cannot be neglected.
| Monatomic | Linear molecules | Non-Linear molecules | |
|---|---|---|---|
| Position (x, y and z) | 3 | 3 | 3 |
| Rotation (x, y and z) | 0 | 2 | 3 |
| Vibration | 0 | 3N - 5 | 3N - 6 |
| Total | 3 | 3N | 3N |
Independent degrees of freedom
The set of degrees of freedom of a system is independent if the energy associated with the set can be written in the following form:
of a system is independent if the energy associated with the set can be written in the following form:
where
 is a function of the sole variable
is a function of the sole variable  .
.example: if
 and
and 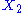 are two degrees of freedom, and
are two degrees of freedom, and  is the associated energy:
is the associated energy:
- If
 , then the two degrees of freedom are independent.
, then the two degrees of freedom are independent. - If
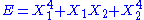 , then the two degrees of freedom are not independent. The term involving the product of
, then the two degrees of freedom are not independent. The term involving the product of 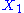 and
and 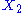 is a coupling term, that describes an interaction between the two degrees of freedom.
is a coupling term, that describes an interaction between the two degrees of freedom.
At thermodynamic equilibrium
Thermodynamic equilibrium
In thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...
,
 are all statistically independent
are all statistically independentStatistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
of each other.
For i from 1 to N, the value of the ith degree of freedom
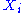 is distributed according to the Boltzmann distribution
is distributed according to the Boltzmann distributionBoltzmann distribution
In chemistry, physics, and mathematics, the Boltzmann distribution is a certain distribution function or probability measure for the distribution of the states of a system. It underpins the concept of the canonical ensemble, providing its underlying distribution...
. Its probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
is the following:
-
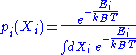 ,
,
In this section, and throughout the article the brackets
 denote the mean
denote the meanMean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
of the quantity they enclose.
The internal energy
Internal energy
In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
of the system is the sum of the average energies associated to each of the degrees of freedom:
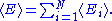
Demonstrations
A system exchanges energy in the form of heat with its surroundings and the number of particles in the system remains fixed. This corresponds to studying the system in the canonical ensemble. Note that in statistical mechanicsStatistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, a result that is demonstrated for a system in a particular ensemble remains true for this system at the thermodynamic limit
Thermodynamic limit
In thermodynamics, particularly statistical mechanics, the thermodynamic limit is reached as the number of particles in a system, N, approaches infinity...
in any ensemble. In the canonical ensemble, at thermodynamic equilibrium
Thermodynamic equilibrium
In thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...
, the state of the system is distributed among all micro-states
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
according to the Boltzmann distribution
Boltzmann distribution
In chemistry, physics, and mathematics, the Boltzmann distribution is a certain distribution function or probability measure for the distribution of the states of a system. It underpins the concept of the canonical ensemble, providing its underlying distribution...
. If
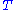 is the system's temperature
is the system's temperatureTemperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
and
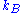 is Boltzmann's constant, then the probability density function
is Boltzmann's constant, then the probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
associated to each micro-state is the following:
-
 ,
,
The denominator in the above expression plays an important role. This expression immediately breaks down into a product of terms depending of a single degree of freedom:
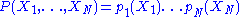
The existence of such a breakdown of the multidimensional probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
into a product of functions of one variable is enough by itself to demonstrate that
 are statistically independent
are statistically independentStatistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
from each other.
Since each function
 is normalized
is normalizedNormalizing constant
The concept of a normalizing constant arises in probability theory and a variety of other areas of mathematics.-Definition and examples:In probability theory, a normalizing constant is a constant by which an everywhere non-negative function must be multiplied so the area under its graph is 1, e.g.,...
, it follows immediately that
 is the probability density function
is the probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of the degree of freedom
 , for i from 1 to N.
, for i from 1 to N.Finally, the internal energy
Internal energy
In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
of the system is its mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
energy. The energy of a degree of freedom
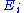 is a function of the sole variable
is a function of the sole variable 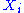 . Since
. Since  are independent
are independentStatistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
from each other, the energies
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
 are also statistically independent
are also statistically independentStatistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
from each other. The total internal energy
Internal energy
In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
of the system can thus be written as:
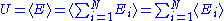
Quadratic degrees of freedom
A degree of freedom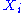 is quadratic if the energy terms associated to this degree of freedom can be written as
is quadratic if the energy terms associated to this degree of freedom can be written as ,
,where
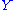 is a linear combination
is a linear combinationLinear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of other quadratic degrees of freedom.
example: if
 and
and 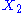 are two degrees of freedom, and
are two degrees of freedom, and  is the associated energy:
is the associated energy:
- If
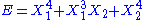 , then the two degrees of freedom are not independent and non-quadratic.
, then the two degrees of freedom are not independent and non-quadratic. - If
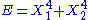 , then the two degrees of freedom are independent and non-quadratic.
, then the two degrees of freedom are independent and non-quadratic. - If
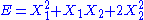 , then the two degrees of freedom are not independent but are quadratic.
, then the two degrees of freedom are not independent but are quadratic. - If
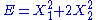 , then the two degrees of freedom are independent and quadratic.
, then the two degrees of freedom are independent and quadratic.
For example, in Newtonian mechanics, the dynamics
Dynamics (mechanics)
In the field of physics, the study of the causes of motion and changes in motion is dynamics. In other words the study of forces and why objects are in motion. Dynamics includes the study of the effect of torques on motion...
of a system of quadratic degrees of freedom are controlled by a set of homogeneous linear differential equation
Linear differential equation
Linear differential equations are of the formwhere the differential operator L is a linear operator, y is the unknown function , and the right hand side ƒ is a given function of the same nature as y...
s with constant coefficients
Constant coefficients
In mathematics, constant coefficients is a term applied to differential operators, and also some difference operators, to signify that they contain no functions of the independent variables, other than constant functions. In other words, it singles out special operators, within the larger class of...
.
Quadratic and independent degree of freedom
 are quadratic and independent degrees of freedom if the energy associated to a microstate of the system they represent can be written as:
are quadratic and independent degrees of freedom if the energy associated to a microstate of the system they represent can be written as: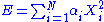
Equipartition theorem
In the classical limit of statistical mechanicsStatistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, at thermodynamic equilibrium
Thermodynamic equilibrium
In thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...
, the internal energy
Internal energy
In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
of a system of N quadratic and independent degrees of freedom is:
Here, the mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
energy associated with a degree of freedom is:
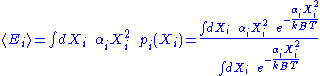
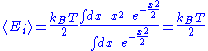
Since the degrees of freedom are independent, the internal energy
Internal energy
In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
of the system is equal to the sum of the mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
energy associated with each degree of freedom, which demonstrates the result.